13.8: Робота і скалярний добуток

Введемо векторну операцію, яка називається скалярним добутком або «точковим добутком», яка приймає будь-які два вектори і генерує скалярну величину (число). Побачимо, що фізична концепція роботи може бути математично описана скалярним добутком між векторами сили і зміщення.

скалярний добуток

\(\overrightarrow{\mathbf{B}}\)Дозволяти\(\overrightarrow{\mathbf{A}}\) і бути двома векторами. Оскільки будь-які два неколінеарних вектора утворюють площину, ми визначаємо кут θ як кут між векторами\(\overrightarrow{\mathbf{A}}\) і\(\overrightarrow{\mathbf{B}}\) як показано на малюнку 13.9. Зверніть увагу, що θ може варіюватися від 0 до\(\pi\).

Малюнок 13.9 Скалярна геометрія виробу.

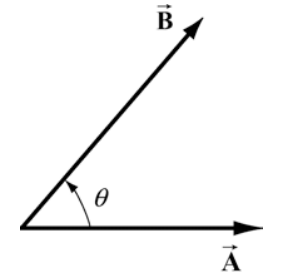
Скалярний\(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}\) добуток векторів\(\overrightarrow{\mathbf{A}}\) і\(\overrightarrow{\mathbf{B}}\) визначається як добуток величини векторів\(\overrightarrow{\mathbf{A}}\) і\(\overrightarrow{\mathbf{B}}\) з косинусом кута θ між двома векторами:

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A B \cos (\theta) \nonumber \]

де\(A=|\overrightarrow{\mathbf{A}}| \text { and } B=\mid \overrightarrow{\mathbf{B}}\) представляють величину\(\overrightarrow{\mathbf{A}}\) і\(\overrightarrow{\mathbf{B}}\) відповідно. Скалярний добуток може бути додатним, нульовим або від'ємним, в залежності від значення\(\cos \theta\). Скалярний добуток - це завжди скалярна величина.

Таким чином, кут, утворений двома векторами

\[\theta=\cos ^{-1}\left(\frac{\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}}{|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}|}\right) \nonumber \]

Величина вектора\(\overrightarrow{\mathbf{A}}\) задається квадратним коренем скалярного добутку вектора\(\overrightarrow{\mathbf{A}}\) з самим собою.

\[|\overrightarrow{\mathbf{A}}|=(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2} \nonumber \]

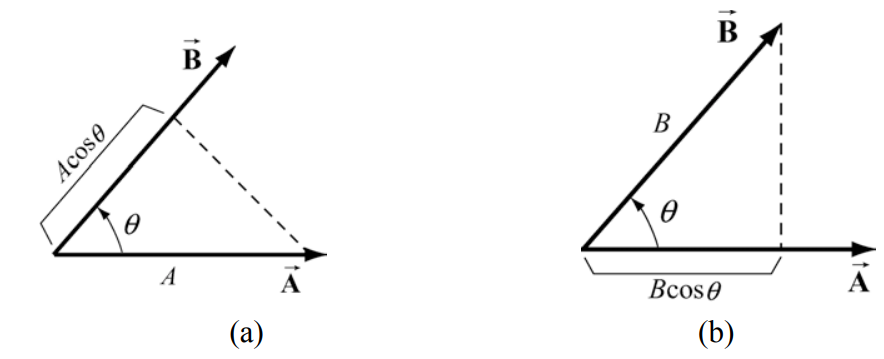
Ми можемо дати геометричну інтерпретацію скалярному добутку, написавши визначення як

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=(A \cos (\theta)) B \nonumber \]

У цій формулюванні термін Acosθ - це проекція вектора\(\overrightarrow{\mathbf{B}}\) в напрямку вектора\(\overrightarrow{\mathbf{B}}\). Ця проекція показана на малюнку 13.10а. Так скалярний добуток є добутком проекції довжини\(\overrightarrow{\mathbf{A}}\) в напрямку\(\overrightarrow{\mathbf{B}}\) з довжиною\(\overrightarrow{\mathbf{B}}\). Зауважте, що ми також могли б записати скалярний добуток як

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A(B \cos (\theta)) \nonumber \]

Тепер термін\(B \cos (\theta)\) - це проекція вектора\(\overrightarrow{\mathbf{B}}\) в напрямку вектора,\(\overrightarrow{\mathbf{A}}\) як показано на малюнку 13.10b. З цієї точки зору скалярний добуток є добутком проекції довжини\(\overrightarrow{\mathbf{B}}\) в напрямку\(\overrightarrow{\mathbf{A}}\) з довжиною\(\overrightarrow{\mathbf{A}}\).

Малюнок 13.10 (a) і (b) Проекція векторів і скалярний добуток

З нашого визначення скалярного добутку ми бачимо, що скалярний добуток двох векторів, які перпендикулярні один одному, дорівнює нулю, оскільки кут між векторами дорівнює\(\pi / 2\) і\(\cos (\pi / 2)=0\).

Ми можемо обчислити скалярний добуток між двома векторами в декартовій системі координат наступним чином. Розглянемо два вектори\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}\) і\(\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\mathbf{k}}\). Нагадаємо, що

\ [\ почати {масив} {л}
\ капелюх {\ mathbf {i}}\ cdot\ капелюх {\ mathbf {i}} =\ капелюх {\ mathbf {j}}\ cdot\ капелюх {\ mathbf {j}} =\ капелюх {\ mathbf {k}}\ cdot\ капелюх {\ mathbf {k}} 1\
\ капелюх {\ mathbf {я}}\ cdot\ капелюх {\ mathbf {j}} =\ капелюх {\ mathbf {j}}\ cdot\ капелюх {\ mathbf {k}} =\ капелюх {\ mathbf {я}}\ cdot\ капелюх {\ mathbf {k}} =0
\ кінець {масив}\ nonumber\]

Скалярний добуток між\(\overrightarrow{\mathbf{A}}\) і\(\overrightarrow{\mathbf{B}}\) є тоді

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \nonumber \]

Похідна за часом скалярного добутку двох векторів задається

\ [\ почати {масив} {l}
\ frac {d} {d t} (\ переправа стрілка {\ mathbf {A}}\ cdot\ overrightarrow {\ mathbf {B}}) =\ frac {d} {d t}\ ліворуч (A_ {x} B_ {x} +A_ {y} B_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +A_ {y} +z} B_ {z}\ праворуч)\\
=\ frac {d} {d t}\ ліворуч (A_ {x}\ праворуч) B_ {x} +\ frac {d} {d t}\ ліворуч (A_ {y}\ праворуч) B_ {y} +\ frac {d} {d t}\ ліворуч (A_ {z}\ праворуч) B_ {y} +\ frac {d}\ ліворуч (A_ {z}\ праворуч) B_ {y} +A_ {x}\ фракція {d} {d t}\ ліворуч (B_ {x}\ праворуч) +A_ {y}\ frac {d} {d t}\ ліворуч (B_ {y}\ праворуч) +A_ {z}\ frac {d} {y}\ ліворуч (B_ {z}\ праворуч)\
=\ ліворуч (\ frac {d} {d}\ overrightaright рядок {\ mathbf {A}}\ праворуч)\ cdot\ переправа стрілка {\ mathbf {B}} +\ переправа стрілка {\ mathbf {A}}\ cdot\ ліворуч (\ frac {d} {d t}\ переправа стрілка {\ mathbf {B}}\ праворуч)
\ end {масив}\ nonumber\]

Зокрема коли\(\overrightarrow{\mathbf{A}}=\overrightarrow{\mathbf{B}}\), то тимчасова похідна квадрата величини вектора\(\overrightarrow{\mathbf{A}}\) задається

\[\frac{d}{d t} A^{2}=\frac{d}{d t}(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})=\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{A}} \cdot\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right)=2\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}} \nonumber \]

Кінетична енергія і скалярний добуток

Для об'єкта, що зазнає тривимірного руху, швидкість об'єкта в декартових складових задається\(\overrightarrow{\mathbf{v}}=v_{x} \hat{\mathbf{i}}+v_{y} \hat{\mathbf{j}}+v_{z} \hat{\mathbf{k}}\). Нагадаємо, що величина вектора задається квадратним коренем скалярного добутку вектора з самим собою,

\[A \equiv|\overrightarrow{\mathbf{A}}| \equiv(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2}=\left(A_{x}^{2}+A_{y}^{2}+A_{z}^{2}\right)^{1 / 2} \nonumber \]

Тому квадрат величини швидкості задається виразом

\[v^{2} \equiv(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \nonumber \]

Звідси кінетична енергія об'єкта задається

\[K=\frac{1}{2} m(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=\frac{1}{2} m\left(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\right) \nonumber \]

Робота і скалярний добуток

Робота є важливим фізичним прикладом математичної операції взяття скалярного добутку між двома векторами. Нагадаємо, що коли на тіло діє постійна сила і точка прикладання сили піддається зміщенню уздовж осі х, тільки складова сили в цьому напрямку сприяє роботі,

\[W=F_{x} \Delta x \nonumber \]

Припустимо, ми тягнемо тіло по горизонтальній поверхні з силою\(\overrightarrow{\mathbf{F}}\). Виберіть такі координати, щоб горизонтальний напрямок був осі x, а сила\(\overrightarrow{\mathbf{F}}\) утворює кут\(\beta\) з додатним x -напрямком. На малюнку 13.11 ми показуємо вектор сили\(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\) і вектор зміщення точки прикладання сили\(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\). Зверніть увагу, що\(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\) є складовою зміщення і, отже, може бути більше, дорівнює або менше нуля (але показано як більше нуля на малюнку для наочності). Скалярний добуток між вектором сили\(\overrightarrow{\mathbf{F}}\) і вектором зміщення\(\Delta \overrightarrow{\mathbf{x}}\) дорівнює

\[\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=\left(F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\right) \cdot(\Delta x \hat{\mathbf{i}})=F_{x} \Delta x \nonumber \]

Малюнок 13.11 Вектори сили і переміщення

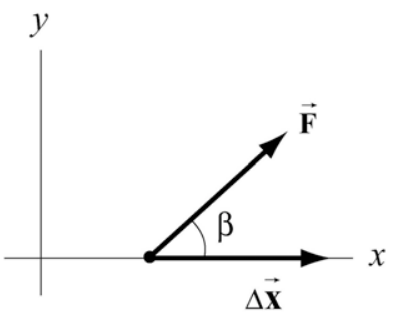
Робота, виконана силою, тоді

\[\Delta W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}} \nonumber \]

В цілому кут\(\beta\) приймає значення в межах діапазону\(-\pi \leq \beta \leq \pi\) (на рис. 13.11,\(0 \leq \beta \leq \pi / 2\)). Оскільки х -складова сили\(F_{x}=F \cos (\beta)\) де\(F=|\overrightarrow{\mathbf{F}}|\) позначає величину, робота\(\overrightarrow{\mathbf{F}}\), виконана силою, є

\[W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=(F \cos (\beta)) \Delta x \nonumber \]

Приклад 13.10 Ковзання об'єкта вниз по похилій площині

Об'єкт масою m = 4,0 кг, починаючи з спокою, ковзає вниз по похилій площині довжиною l = 3,0 м. Площина нахилена під кутом\(\theta=30^{\circ}\) до землі. Коефіцієнт кінетичного тертя є\(\mu_{k}=0.2\) (а) Яка робота виконується кожною з трьох сил, поки об'єкт ковзає вниз по похилій площині? (б) Для кожної сили робота, виконана силою, позитивна чи негативна? (c) Яка сума роботи, виконаної трьома силами? Це позитивне чи негативне?

Рішення: (a) і (b) Виберіть систему координат з початком у верхній частині похилої площини і додатним x -напрямком, спрямованим вниз по похилій площині, а позитивним y - напрямком, спрямованим вгорі праворуч, як показано на малюнку 13.12. Поки об'єкт ковзає вниз по похилій площині, на об'єкт діють три рівномірні сили, гравітаційна сила, яка вказує вниз і має величину\(F_{g}=m g\), нормальна сила N, яка перпендикулярна поверхні похилої площини, і сила тертя, яка протистоїть руху і дорівнює в величина до\(f_{k}=\mu_{k} N\). Схема сили на об'єкті показана на малюнку 13.13.

Малюнок 13.12 Система координат об'єкта, що ковзає по похилій площині

Малюнок 13.13 Діаграма сили вільного тіла для об'єкта

Для того щоб розрахувати роботу нам потрібно визначити, які сили мають складову в напрямку зміщення. Тільки складова сили тяжіння по позитивному х -напрямку\(F_{g x}=m g \sin \theta\) і сила тертя спрямовані уздовж зміщення і тому сприяють роботі. Нам потрібно використовувати Другий закон Ньютона, щоб визначити величини нормальної сили. Оскільки об'єкт обмежений рухатися вздовж позитивного x -напрямку\(a_{y}=0\), Другий закон Ньютона у\(\hat{\mathbf{j}}\) напрямку -direction\(N-m g \cos \theta=0\). Тому\(N=m g \cos \theta\) і величина сили тертя є\(f_{k}=\mu_{k} m g \cos \theta\).

При виборі нами системи координат з початком у верхній частині похилої площини і додатним х -напрямком, спрямованим вниз по похилій площині, зміщення об'єкта задається вектором\(\Delta \overrightarrow{\mathbf{r}}=\Delta x \hat{\mathbf{i}}\) (рис. 13.14).

Малюнок 13.14 Вектори сили та вектор зміщення об'єкта

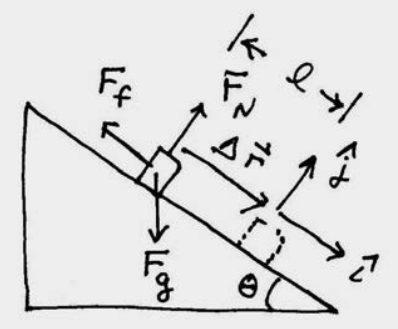
Векторне розкладання трьох сил є\(\overrightarrow{\mathbf{F}}^{g}=m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}\)\(\overrightarrow{\mathbf{F}}^{f}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}}\), і\(\overrightarrow{\mathbf{F}}^{N}=m g \cos \theta \hat{\mathbf{j}}\). Робота, виконана нормальною силою, дорівнює нулю, оскільки нормальна сила перпендикулярна зміщенню.

\[W^{N}=\overrightarrow{\mathbf{F}}^{N} \cdot \Delta \overrightarrow{\mathbf{r}}=m g \cos \theta \hat{\mathbf{j}} \cdot l \hat{\mathbf{i}}=0 \nonumber \]

Тоді робота, виконана силою тертя, негативна і дається

\[W^{f}=\overrightarrow{\mathbf{F}}^{f} \cdot \Delta \overrightarrow{\mathbf{r}}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}} \cdot l \hat{\mathbf{i}}=-\mu_{k} m g \cos \theta l<0 \nonumber \]

Підстановка у відповідні значення дає

\[W^{f}=-\mu_{k} m g \cos \theta l=-(0.2)(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\cos \left(30^{\circ}\right)(3.0 \mathrm{m})=-20.4 \mathrm{J}\right. \nonumber \]

Робота, виконана гравітаційною силою, є позитивною і дається

\[W^{g}=\overrightarrow{\mathbf{F}}^{g} \cdot \Delta \overrightarrow{\mathbf{r}}=(m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}) \cdot l \hat{\mathbf{i}}=m g l \sin \theta>0 \nonumber \]

Підстановка у відповідні значення дає

\[W^{g}=m g l \sin \theta=(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\sin \left(30^{\circ}\right)=58.8 \mathrm{J}\right. \nonumber \]

(c) Скалярна сума роботи, виконаної трьома силами, тоді

\ [\ почати {масив} {l}
W=W^ {g} +W^ {f} =м г л\ лівий (\ sin\ тета-\ mu_ {k}\ cos\ тета\ вправо)\\
W =( 4.0\ mathrm {кг})\ лівий (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч) (3,0\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч) (3,0\ mathrm {m} thrm {m})\ лівий (\ sin\ лівий (30^ {\ circ}\ праворуч) - (0.2)\ лівий (\ cos\ лівий (30^ {\ circ}\ праворуч)\ праворуч) =38,4\ mathrm {J}. \ праворуч.
\ end {масив}\ nonumber\]