13.7: Потужність, що застосовується постійною силою

Припустимо, що прикладена сила\(\overrightarrow{\mathbf{F}}^{a}\) діє на тіло протягом часового інтервалу\(\Delta t\) і зміщення точки прикладання сили знаходиться в х -напрямку на величину\(\Delta x\). Робота, виконана\(\Delta W^{a}\), протягом цього інтервалу

\[\Delta W^{a}=F_{x}^{a} \Delta x \nonumber \]

де\(F_{x}^{a}\) - х -складова прикладеної сили. (Рівняння (13.7.1) таке ж, як і рівняння (13.4.2).)

Середня потужність прикладеної сили визначається як швидкість, з якою виконується робота,

\[P_{a v e}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a} v_{\text {ave }, x} \nonumber \]

Середня потужність, що подається тілу, дорівнює складової сили в напрямку руху, що умножується на складову середньої швидкості тіла. Потужність - скалярна величина і може бути позитивною, нульовою або негативною в залежності від ознаки роботи. Одиниці потужності СІ називаються ватами [Вт] і\([1 \mathrm{W}]=\left[1 \mathrm{J} \cdot \mathrm{s}^{-1}\right]\).

Миттєва потужність в момент t визначається як межа середньої потужності, оскільки часовий інтервал\([t, t+\Delta t]\) наближається до нуля,

\[P^{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta W^{a}}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a}\left(\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\right)=F_{x}^{a} v_{x} \nonumber \]

Миттєва сила постійної прикладеної сили є добутком складової сили в напрямку руху і миттєвої швидкості рухомого об'єкта.

Приклад\(\PageIndex{1}\): Gravitational Power for a Falling Object

Припустимо, куля маси\(m=0.2 \mathrm{kg}\) починається з спокою на висоті\(y_{0}=15 \mathrm{m}\) над поверхнею землі і падає на висоту\(y_{f}=5.0 \mathrm{m}\) над поверхнею землі. Яку середню потужність надає сила тяжіння? Яка миттєва потужність, коли куля знаходиться на висоті\(y_{f}=5.0 \mathrm{m}\) над поверхнею Землі? Складіть графік потужності проти часу. Ви можете ігнорувати наслідки опору повітря.

Рішення

Існує два шляхи вирішення цієї проблеми. Обидва підходи вимагають обчислення\(\Delta t\) часового інтервалу падіння м'яча. Встановити\(t_{0}=0\) на час, коли м'яч був випущений. Ми можемо вирішити за часовий проміжок\(\Delta t=t_{f}\), що куля падає, використовуючи рівняння для вільно падаючого об'єкта, який починається з відпочинку,

\[y_{f}=y_{0}-\frac{1}{2} g t_{f}^{2} \nonumber \]

Таким чином, часовий проміжок для падіння дорівнює

\[t_{f}=\sqrt{\frac{2}{g}\left(y_{0}-y_{f}\right)}=\sqrt{\frac{2}{9.8 \mathrm{m} \cdot \mathrm{s}^{-2}}(15 \mathrm{m}-5 \mathrm{m})}=1.4 \mathrm{s} \nonumber \]

Перший підхід: ми можемо розрахувати роботу, виконану самопливом,

\ [\ почати {вирівняний}
W^ {g} &=-м г\ ліворуч (y_ {f} -y_ {0}\ праворуч)\\
&=\ ліворуч (-2.0\ раз 10^ {-1}\ mathrm {kg}\ праворуч)\ ліворуч (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч) (5\ mathrm {m} -15\ mathrm {m}) =2.0\ раз 10^ {1}\ mathrm {J}
\ кінець {вирівняний}\ номер\]

Тоді середня потужність дорівнює

\[P_{\text {ave }}^{g}=\frac{\Delta W}{\Delta t}=\frac{2.0 \times 10^{1} \mathrm{J}}{1.4 \mathrm{s}}=1.4 \times 10^{1} \mathrm{W} \nonumber \]

Другий підхід. Розрахуємо силу тяжіння і середню швидкість. Сила тяжіння

\[F_{y}^{g}=-m g=-\left(2.0 \times 10^{-1} \mathrm{kg}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)=-2.0 \mathrm{N} \nonumber \]

Середня швидкість

\[v_{\text {ave } y}=\frac{\Delta y}{\Delta t}=\frac{5 \mathrm{m}-15 \mathrm{m}}{1.4 \mathrm{s}}=-7.0 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

Отже, середня потужність

\ [\ почати {вирівняний}
P_ {\ текст {ave}} ^ {г} &=F_ {y} ^ {g} v_ {\ текст {ave} y} =( -m g) v_ {\ текст {ave}, y}\\
& =( -2.0\ mathrm {N})\ лівий (-7.0\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ праворуч) =1.4\ раз 10^ {1}\ mathrm {W}
\ кінець {вирівняний}\ номер\]

Для того, щоб знайти миттєву потужність в будь-який момент, нам потрібно знайти миттєву швидкість в той час. М'ячу потрібен час\(t_{f}=1.4 \mathrm{s}\), щоб досягти висоти\(y_{f}=5.0 \mathrm{m}\). Швидкість на цій висоті задається

\[v_{y}=-g t_{f}=-\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(1.4 \mathrm{s})=-1.4 \times 10^{1} \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

Таким чином, миттєва потужність в часі\(t_{f}=1.4 \mathrm{s}\)

\ [\ почати {вирівняний} Р
^ {г} &=F_ {y} ^ {g} v_ {y} =( -м г)\ ліворуч (-g t_ {f}\ праворуч) =m g^ {2} t_ {f}\\
& =( 0,2\ mathrm {кг})\ лівий (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч) ^ {2} (1.4\ mathrm {s}) =2.7\ раз 10^ {1}\ mathrm {W}
\ кінець {вирівняний}\ number\]

Якби ця задача була виконана символічно, відповіді, наведені в Рівнянні (13.7.11) та Рівняння (13.7.12), відрізнялися б у два рази; відповіді були округлені до двох значущих цифр.

Миттєва потужність зростає лінійно з часом. Графік потужності проти часу показаний на малюнку 13.8. З малюнка слід бачити, що миттєва потужність в будь-який момент в два рази перевищує середню потужність між t = 0 і тим часом.

Малюнок 13.8 Графік потужності проти часу

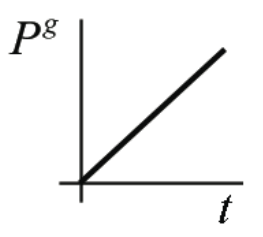
Приклад\(\PageIndex{2}\): Power Pushing a Cup

Людина штовхає чашку масою 0,2 кг по горизонтальному столу з силою величиною 2,0 Н під кутом по відношенню до горизонталі на відстань 0,5 м, як в прикладі 13.4.\(30^{\circ}\) Коефіцієнт тертя між столом і чашкою дорівнює\(\mu_{k}=0.1\). Яка середня потужність сили штовхання? Яка середня потужність кінетичної сили тертя?

Рішення

Ми будемо використовувати результати з прикладів 13.4 і 13.7, але зберігаючи додаткові значні цифри в проміжних розрахунках. Робота, виконана силою натискання, є

\[W^{a}=F_{x}^{a}\left(x_{f}-x_{0}\right)=(1.732 \mathrm{N})(0.50 \mathrm{m})=8.660 \times 10^{-1} \mathrm{J} \nonumber \]

Кінцева швидкість чашки -\(v_{x, f}=2.860 \mathrm{m} \cdot \mathrm{s}^{-1}\). Припускаючи постійне прискорення, час, протягом якого чаша була штовхнута, становить

\[t_{f}=\frac{2\left(x_{f}-x_{0}\right)}{v_{x, f}}=0.3496 \mathrm{s} \nonumber \]

Середня потужність сили штовхання тоді, з\(\Delta t=t_{f}\),

\[P_{\text {ave }}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{8.660 \times 10^{-1} \mathrm{J}}{0.3496 \mathrm{s}}=2.340 \mathrm{W} \nonumber \]

або 2,3 Вт до двох значущих цифр. Робота, виконана силою тертя, є

\ [\ почати {вирівняний}
W^ {f} &=f_ {\ mathrm {k}}\ ліворуч (x_ {f} -x_ {0}\ праворуч)\\
&=-\ mu_ {\ mathrm {k}} N\ ліворуч (x_ {f} -x_ {0}\ праворуч) =-\ ліворуч (9.6\ раз 10^ {-2}\ mathrm {N}\ праворуч) (0.50\ mathrm {m}) =-\ ліворуч (4.8\ раз 10^ {-2}\ mathrm {J}\ праворуч)
\ кінець {вирівняний}\ nonumber\]

Середня потужність кінетичного тертя дорівнює

\[P_{\text {ave }}^{f}=\frac{\Delta W^{f}}{\Delta t}=\frac{-4.8 \times 10^{-2} \mathrm{J}}{0.3496 \mathrm{s}}=-1.4 \times 10^{-1} \mathrm{W} \nonumber \]

Часова швидкість зміни кінетичної енергії для тіла маси m, що рухається у напрямку x, дорівнює

\[\frac{d K}{d t}=\frac{d}{d t}\left(\frac{1}{2} m v_{x}^{2}\right)=m \frac{d v_{x}}{d t} v_{x}=m a_{x} v_{x} \nonumber \]

За другим законом Ньютона,\(F_{x}=m a_{x}\) і так рівняння (13.7.18) стає

\[\frac{d K}{d t}=F_{x} v_{x}=P \nonumber \]

Миттєва потужність, що подається тілу, дорівнює тимчасовій швидкості зміни кінетичної енергії тіла.