13.9: Робота, виконана непостійною силою вздовж довільного шляху

Припустимо, що непостійна сила\(\overrightarrow{\mathbf{F}}\) діє на точкове тіло масою m, поки тіло рухається по тривимірному вигнутому шляху. Вектор положення тіла в момент t щодо вибору походження є\(\overrightarrow{\mathbf{r}}(t)\). На малюнку 13.15 ми показуємо орбіту тіла за часовий проміжок, що\(\left[t_{i}, t_{f}\right]\) рухається з початкового положення\(t=t_{i}\) в\(\overrightarrow{\mathbf{r}}_{i} \equiv \overrightarrow{\mathbf{r}}\left(t=t_{i}\right)\) момент часу в\(\overrightarrow{\mathbf{r}}_{f} \equiv \overrightarrow{\mathbf{r}}\left(t=t_{f}\right)\) кінцеве положення\(t=t_{f}\).

Малюнок 13.15 Шляхи простежуються рухом тіла.

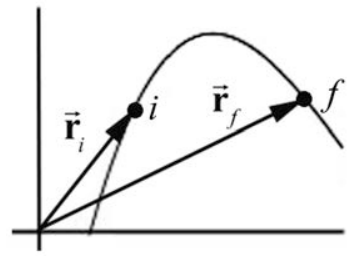
Ділимо часовий проміжок\(\left[t_{i}, t_{f}\right]\) на N менших інтервалів с\(\left[t_{j-1}, t_{j}\right]\),\(j=1, \cdots, N\) с\(t_{N}=t_{f}\). Розглянемо два вектори положення\(\overrightarrow{\mathbf{r}}_{j} \equiv \overrightarrow{\mathbf{r}}\left(t=t_{j}\right)\) та\(\overrightarrow{\mathbf{r}}_{j-1} \equiv \overrightarrow{\mathbf{r}}\left(t=t_{j-1}\right)\) вектор зміщення протягом відповідного часового інтервалу як\(\Delta \overrightarrow{\mathbf{r}}_{j}=\overrightarrow{\mathbf{r}}_{j}-\overrightarrow{\mathbf{r}}_{j-1}\). Нехай\(\overrightarrow{\mathbf{F}}\) позначають силу, що діє на тіло протягом проміжку\(\left[t_{j-1}, t_{j}\right]\). Середня сила в цьому інтервалі становить\(\left(\overrightarrow{\mathbf{F}}_{j}\right)_{\mathrm{ave}}\) і середня робота,\(\Delta W_{j}\) виконана силою протягом часового інтервалу,\(\left[t_{j-1}, t_{j}\right]\) є скалярним добутком між вектором середньої сили і вектором зміщення,

\[\Delta W_{j}=\left(\overrightarrow{\mathbf{F}}_{j}\right)_{\mathrm{ave}} \cdot \Delta \overrightarrow{\mathbf{r}}_{j} \nonumber \]

Вектори сили і зсуву для часового інтервалу\(\left[t_{j-1}, t_{j}\right]\) показані на малюнку 13.16 (зверніть увагу, що індекс «ave» on\(\left(\overrightarrow{\mathbf{F}}_{j}\right)_{\mathrm{ave}}\) був придушений).

Малюнок 13.16 Нескінченно малий робочий елемент.

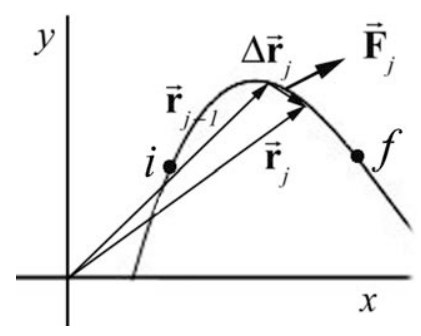
Обчислюємо роботу шляхом додавання цих скалярних внесків до роботи для кожного інтервалу\(\left[t_{j-1}, t_{j}\right]\), для j =1 до N,

\[W_{N}=\sum_{j=1}^{j=N} \Delta W_{j}=\sum_{j=1}^{j=N}\left(\overrightarrow{\mathbf{F}}_{j}\right)_{\mathrm{ave}} \cdot \Delta \overrightarrow{\mathbf{r}}_{j} \nonumber \]

Ми хотіли б визначити роботу таким чином, який не залежить від того, як ми ділимо інтервал, тому ми беремо межу як\(N \rightarrow \infty\) і\(\left|\Delta \overrightarrow{\mathbf{r}}_{j}\right| \rightarrow 0\) для всіх j. У цій межі, коли інтервали стають все меншими і меншими, різниця між середньою силою та фактичною силою зникає. Таким чином, якщо ця межа існує і чітко визначена, то робота, виконана силою

\[W=\lim _{N \rightarrow \infty \atop\left|\Delta \overrightarrow{\mathbf{r}}_{j}\right| \rightarrow 0} \sum_{j=1}^{j=N}\left(\overrightarrow{\mathbf{F}}_{j}\right)_{\text {ave }} \cdot \Delta \overrightarrow{\mathbf{r}}_{j}=\int_{i}^{f} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}} \nonumber \]

Зверніть увагу, що це підсумовування передбачає додавання скалярних величин. Ця межа називається лінійним інтегралом сили\(\overrightarrow{\mathbf{F}}\). Символ\(d \overrightarrow{\mathbf{r}}\) називається нескінченно малим елементом векторної лінії. За часом t,\(d \overrightarrow{\mathbf{r}}\) є дотичною до орбіти тіла і є межею вектора зміщення,\(\Delta \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}(t+\Delta t)-\overrightarrow{\mathbf{r}}(t)\) оскільки Δt наближається до нуля. У цій межі параметр t не відображається у виразі в Рівнянні (13.8.19).

Загалом цей лінійний інтеграл залежить від конкретного шляху, який тіло займає між початковим положенням\(\overrightarrow{\mathbf{r}}_{i}\) і кінцевим положенням\(\overrightarrow{\mathbf{r}}_{f}\), що має значення, коли сила\(\overrightarrow{\mathbf{F}}\) непостійна в просторі, і коли внесок у роботу може змінюватися на різних шляхах у просторі. Ми можемо представити інтеграл у Equation (13.8.19) явно в системі координат, вказавши нескінченно малий векторний лінійний елемент d,\(\overrightarrow{\mathbf{r}}\) а потім явно обчислюючи скалярний добуток.

Робота інтеграла в декартових координатах

У декартових координатах лінійний елемент

\[d \overrightarrow{\mathbf{r}}=d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}}+d z \hat{\mathbf{k}} \nonumber \]

де dx, dy та dz представляють довільні переміщення в\(\hat{\mathbf{i}}-, \hat{\mathbf{j}}-\), і\(\hat{\mathbf{k}}\) -напрямку відповідно, як показано на малюнку 13.17.

Малюнок 13.17 Лінійний елемент в декартових координатах.

Вектор сили можна представити в векторних позначеннях

\[\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}+F_{z} \hat{\mathbf{k}} \nonumber \]

Нескінченно мала робота - це сума роботи, виконаної складовою сили, що умножує складову переміщення в кожному напрямку,

\[d W=F_{x} d x+F_{y} d y+F_{z} d z \nonumber \]

Рівняння (13.8.22) - це всього лише скалярний добуток

\ [\ почати {вирівняний}
д W &=\ переправа стрілка {\ mathbf {F}}\ cdot d\ overrightarrow {\ mathbf {r}} =\ ліворуч (F_ {x}\ hat {\ mathbf {i}} +F_ {y}\ шапка {\ mathbf {j}} +F_ {z}\ капелюх {mathbf {k}}\ праворуч)\ cdot (д х\ капелюх {\ mathbf {я}} +д у\ капелюх {\ mathbf {j}} +д з\ капелюх {\ mathbf {k}})\\
&=F_ {x} d x+F_ {y} d y+f_ {z} d
\ end {вирівняний}\ nonumber\]

Робота - це

\[W=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}}\left(F_{x} d x+F_{y} d y+F_{z} d z\right)=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} F_{x} d x+\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} \cdot \overrightarrow{d y+\int_{z=\overrightarrow{\mathbf{r}}_{0}}} F_{z} d z \nonumber \]

Робота інтеграла в циліндричних координатах

У циліндричних координатах лінійний елемент

\[d \overrightarrow{\mathbf{r}}=d r \hat{\mathbf{r}}+r d \theta \hat{\mathbf{\theta}}+d z \hat{\mathbf{k}} \nonumber \]

де dr, rdθ і dz представляють довільні переміщення в\(\hat{\mathbf{r}}-, \hat{\boldsymbol{\theta}}-\) і\(\hat{\mathbf{k}}-\) напрямках відповідно, як показано на малюнку 13.18.

Малюнок 13.18 Вектор зміщення\(d \overrightarrow{\mathbf{s}}\) між двома точками

Вектор сили можна представити в векторних позначеннях

\[\overrightarrow{\mathbf{F}}=F_{r} \hat{\mathbf{r}}+F_{\theta} \hat{\boldsymbol{\theta}}+F_{z} \hat{\mathbf{k}} \nonumber \]

Нескінченно мала робота - скалярний добуток

\ [\ почати {вирівняний}
d W &=\ переправа стрілка {\ mathbf {F}}\ cdot d\ overrightarrow {\ mathbf {r}} =\ ліворуч (F_ {r}\ hat {\ mathbf {r}} +F_ {\ theta}\ hat {\ theta}\ mathbf {k}}\ право)\ cdot (d r\ hat {\ mathbf {r}} +r д\ тета\ капелюх {\ жирний символ {\ тета}} +д з\ капелюх {\ mathbf {k}})\
&=F _ {r} д R+f_ {\ тета} r д\ тета+F_ {z} d z
\ кінець {вирівняний}\ nonumber\]

Робота - це

\[W=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} \cdot \overrightarrow{\mathbf{r}}=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}}\left(F_{r} d r+F_{\theta} r d \theta+F_{z} d z\right)=\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} F_{r} d r+\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} F_{\theta} r d \theta+\int_{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{0}}^{\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{f}} F_{z} d z \nonumber \]