18.2: Затухаючий керований осцилятор

Лінійний демпфірованний керований генератор:

\ begin {рівняння}
\ ddot {x} +2\ лямбда\ точка {x} +\ омега_ {0} ^ {2} x =( f/м) e^ {i\ Omega t}
\ end {рівняння}

(Після позначення Ландау тут - зверніть увагу, що це означає, що фактична сила тертя є$2 \lambda m \dot{x}$)

Дивлячись поблизу резонансу для розв'язків сталого стану на рушійній частоті, з амплітудою$b$, фазовим відставанням$\delta$, тобто

$x(t)=b e^{i(\Omega t+\delta)}$, знаходимо

\ begin {рівняння}
b e^ {i\ дельта}\ ліво (-\ Омега^ {2} +2 i\ лямбда\ Омега+\ омега_ {0} ^ {2}\ праворуч) =( f/m)
\ end {рівняння}

Для майже резонансної частоти водіння$\Omega=\omega_{0}+\varepsilon$, і припускаючи, що демпфування буде досить малим, що ми можемо скинути$\varepsilon \lambda$ термін разом з$\varepsilon^{2}$, провідні терміни порядку дають

\ begin {рівняння}
b e^ {i\ дельта} =-f/2 м (\ варепсилон-i\ лямбда)\ omega_ {0}
\ end {рівняння}

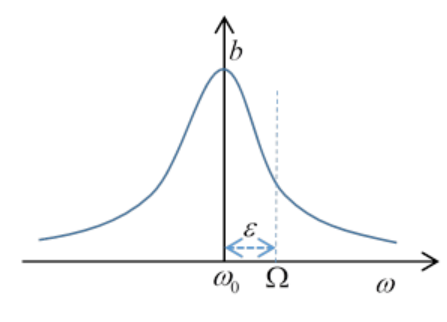
тому реакція, залежність амплітуди коливань від частоти, до цієї точності

\ почати {рівняння}
b=\ frac {f} {2 м\ омега_ {0}\ sqrt {\ ліворуч (\ Омега-\ омега_ {0}\ праворуч) ^ {2} +\ лямбда-^ {2}} =\ frac {f} {2 м\ омега_ {0}\ sqrt {\ varepsilon^ {2} +\ лямбда ^ {2}}}
\ end {рівняння}

(Ми також можемо відзначити, що резонансна частота сама по собі знижується демпфуванням, але це ще один ефект другого порядку, який ми ігноруємо тут.)

Швидкість поглинання енергії дорівнює втраті на тертя. Сила тертя$2 \lambda m \dot{x}$ на масу, що$\dot{x}$ рухається при, робить роботу зі швидкістю:

\ begin {рівняння}
2\ лямбда м\ точка {\ точка {x}} ^ {2} =\ лямбда м b^ {2}\ Омега^ {2}
\ end {рівняння}

Половина ширини резонансної кривої як функція рушійної частоти$\Omega$ задається демпфуванням. Загальна площа під кривою не залежить від демпфування.

Для подальшого використання ми напишемо вищевказане рівняння для амплітуди як

$b^{2}\left(\varepsilon^{2}+\lambda^{2}\right)=\frac{f^{2}}{4 m^{2} \omega_{0}^{2}}$