3: Фотографії Шредінгера та Гейзенберга

Поки ми припускали, що квантові стани, що\(|\psi(t)\rangle\) описують систему, несуть залежність від часу. Однак це не єдиний спосіб відстежувати еволюцію часу. Оскільки всі фізично спостережувані величини є очікуваними значеннями, ми можемо записати

\ [\ begin {вирівняний}
\ лангл A\ діапазон &=\ ім'я оператора {Tr} [|\ psi (t)\ діапазон\ лангл\ psi (t) | A] =\ ім'я оператора {Tr}\ лівий [U (t) |\ psi (0)\ діапазон\ лангл\ psi (0) | U^ {\ кинджал} (t)]\\
&=\ ім'я оператора {Tr}\ лівий [|\ psi (0)\ діапазон\ ланголь\ psi (0) | U^ {\ кинджал} (t) A U (t)\ праворуч]\ quad\ text {( циклічна властивість)}\\
&\ equiv\ ім'я оператора {Tr} [|\ psi (0)\ діапазон\ лангл\ psi (0) | A (t)],
\ end {вирівняний}\ тег {3.1}\]

де ми визначили оператор, що змінюється в часі\(A(t)=U^{\dagger}(t) A U(t)\). Зрозуміло, що ми можемо відстежувати еволюцію часу в операторах!

• Шредінгер картина: стежити за еволюцією часу в державах,
• Зображення Гейзенберга: Слідкуйте за еволюцією часу в операторах.

Ми можемо позначити стани та оператори «\(S\)» та «\(H\)» залежно від зображення. Наприклад,

\[\left|\psi_{H}\right\rangle=\left|\psi_{S}(0)\right\rangle \quad \text { and } \quad A_{H}(t)=U^{\dagger}(t) A_{S} U(t)\tag{3.2}\]

Еволюція часу для станів задається рівнянням Шредінгера, тому ми хочемо відповідне «рівняння Гейзенберга» для операторів. По-перше, ми спостерігаємо, що

\[U(t)=\exp \left(-\frac{i}{\hbar} H t\right),\tag{3.3}\]

такий, що

\[\frac{d}{d t} U(t)=-\frac{i}{\hbar} H U(t)\tag{3.4}\]

Далі обчислюємо похідну за часом\(\langle A\rangle\):

\[\frac{d}{d t} \operatorname{Tr}\left[\left|\psi_{S}(t)\right\rangle\left\langle\psi_{S}(t)\right| A_{S}\right]=\frac{d}{d t}\left\langle\psi_{S}(t)\left|A_{S}\right| \psi_{S}(t)\right\rangle=\frac{d}{d t}\left\langle\psi_{H}\left|A_{H}(t)\right| \psi_{H}\right\rangle\tag{3.5}\]

Останнє рівняння випливає з ур. (3.1). Тепер ми можемо обчислити

\ [\ почати {вирівняний}
\ розрив {d} {d t}\ лівий\ лангель\ psi_ {S} (t)\ ліворуч | A_ {S}\ праворуч |\ psi_ {S} (t)\ праворуч\ діапазон &=\ frac {d} {d t}\ ліворуч\ лангель\ psi_ {S} (0)\ ліворуч\ кинджал (t) A_ {S} U (t)\ праворуч |\ psi_ {S} (0)\ вправо\ діапазон\\
&=\ лівий\ лангл\ psi_ {S} (0)\ ліворуч [\ точка {U} ^ {\ кинджал} (t) A_ {S} U (t) +U ^ {\\ кинджал} (t)\ точка {A} _ {S} U (t) +U^ {\ кинджал} (t) A_ {S}\ точка {U} (t)\ праворуч |\ psi_ {S} (0)\ вправо\ діапазон\\
&=\ лівий\ лангель\ psi_ {H}\ ліворуч |\ ліворуч [\ frac {i} {бар} H A_ {H} (t) -\ frac {i} {\ hbar} A_ {H} (t) H+\ frac {\ часткове A_ {H} (t)} {\ часткове t}\ право]\ правий |\ psi_ {H}\ правий\ діапазон\\
&=-\ frac {i } {\ hbar}\ ліворуч\ лангле\ psi_ {H}\ ліворуч |\ ліворуч [A_ {H} (t), H\ праворуч |\ psi_ {H}\ праворуч\ діапазон+\ ліворуч\ лангле\ psi_ {H}\ ліворуч |\ frac {\ часткове A_ {H} (t)} {\ часткове t}\ праворуч |\ psi_ {H}\ праворуч\ діапазон\\
&=\ лівий\ ланкут\ psi_ {H}\ ліворуч |\ frac {d A_ {H} (t)} {d t}\ праворуч |\ psi_ {H}\ правий\ діапазон
\ кінець {вирівняний}\ тег {3.6}\]

Оскільки це має бути вірним для всіх\(\left|\psi_{H}\right\rangle\), це ідентифікатор оператора:

\[\frac{d A_{H}(t)}{d t}=-\frac{i}{\hbar}\left[A_{H}(t), H\right]+\frac{\partial A_{H}(t)}{\partial t}\tag{3.7}\]

Це рівняння Гейзенберга. Зверніть увагу на різницю між «прямим\(d\)» і «фігурним\(\partial\)» в похідній за часом і частковою похідною за часом відповідно. Часткова похідна має справу тільки з явною залежністю від часу оператора. У багатьох випадках (таких як позиція та імпульс) це нуль.

Ми бачили, що і рівняння Шредінгера, і Гейзенберга випливають з гільбертового космічного формалізму квантової механіки фон Неймана. Отже, ми довели, що цей формалізм належним чином об'єднує як хвильову механіку Шредінгера, так і матричну механіку Гейзенберга, Борна і Джорданса.

Як приклад розглянемо кубіт з часом еволюції, визначеної гамільтоном\(H=\frac{1}{2} \hbar \omega Z\), с\(Z=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\). Це може бути спин в магнітному полі, наприклад, таке, що\(\omega=-e B / m c\). Ми хочемо обчислити еволюцію часу оператора\(X_{H}(t)\). Оскільки ми працюємо в картині Гейзенберга поодинці, ми опустимо індекс\(H\). Спочатку оцінюємо комутатор в рівнянні Гейзенберга

\[i \hbar \frac{1}{2} \frac{d X}{d t}=\frac{1}{2}[X, H]=-i \hbar \frac{\omega}{2}Y,\tag{3.8}\]

де ми визначили\(Y=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)\). Отже, тепер ми\(Y\) також повинні знати еволюцію часу:

\[i \hbar \frac{1}{2} \frac{d Y}{d t}=\frac{1}{2}[Y, H]=i \hbar \frac{\omega}{2} X\tag{3.9}\]

Це два зв'язаних лінійних рівняння, які відносно легко вирішити:

\[\dot{X}=-\omega Y \quad \text { and } \quad \dot{Y}=\omega X \quad \text { and } \quad \dot{Z}=0\tag{3.10}\]

Ми можемо визначити два нових\(S_{\pm}=X \pm i Y\) оператори та отримати

\[\dot{S}_{\pm}=-\omega Y \pm i \omega X=\pm i \omega S_{\pm}.\tag{3.11}\]

Рішення цих двох рівнянь дає\(S_{\pm}(t)=S_{\pm}(0) e^{\pm i \omega t}\) результат, і це призводить до

\ [\ почати {вирівняний}
X (t) &=\ розриву {S_ {+} (t) +S_ {-} (t)} {2} =\ розриву {S_ {+} (0) e^ {i\ омега т} +S_ {-} (0) e^ {-i\ омега т}} {2}\
&=\ frac {1} {2}\ ліворуч [X (0) e^ {i\ омега т} +i Y (0) e^ {i\ омега т} +X (0) e^ {-i\ омега т} -i Y (0) e^ {-i\ омега т}\ праворуч]\\
&= X (0)\ cos (\ омега т) -Y (0) \ sin (\ омега т).
\ end {вирівняний}\ tag {3.12}\]

Вас просять показати, що\(Y(t)=Y(0) \cos (\omega t)+X(0) \sin (\omega t)\) у вправі 3.

Ми зараз беремо\(\left|\psi_{H}\right\rangle=|0\rangle\) і\(X(0)=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)\),\(Y(0)=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)\). Очікуване значення\(X(t)\) потім легко обчислюється, щоб бути

\[\langle 0|X(t)| 0\rangle=\cos (\omega t)\langle 0|X(0)| 0\rangle-\sin (\omega t)\langle 0|Y(0)| 0\rangle=0\tag{3.13}\]

Як варіант, коли\(\left|\psi_{H}\right\rangle=|\pm\rangle\), ми знаходимо

\[\langle+|X(t)|+\rangle=\cos (\omega t) \quad \text { and } \quad\langle+|Y(t)|+\rangle=\sin (\omega t)\tag{3.14}\]

Це кругові рухи в часі:

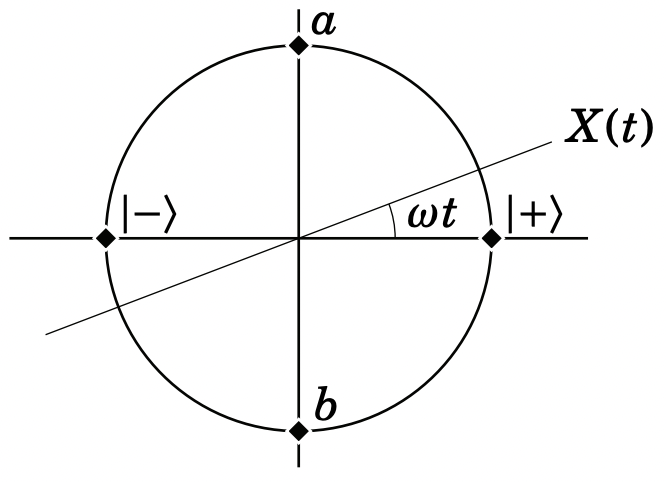
Власний стан\(X(\pi / 2)\) - точка\(a\), а власний стан\(X(-\pi / 2)\) - точка\(b\). Крім того\(X(\pm \pi / 2)=\mp Y(0)\), і стани в точці\(a\) і\(b\), отже, є власними станами\(Y\):

\[\left|\psi_{a}\right\rangle=\frac{|0\rangle-i|1\rangle}{\sqrt{2}} \quad \text { and } \quad\left|\psi_{b}\right\rangle=\frac{|0\rangle+i|1\rangle}{\sqrt{2}}\tag{3.15}\]

Природне питання, яке потрібно задати, - де держави\(|0\rangle\) і\(|1\rangle\) вписуються в цю картину. Це власні стани оператора\(Z\), які ми використовували для генерації унітарної еволюції часу. Зрозуміло, що стани на колі ніколи не стають\(|0\rangle\) або\(|1\rangle\), тому нам потрібно додати ще один вимір:

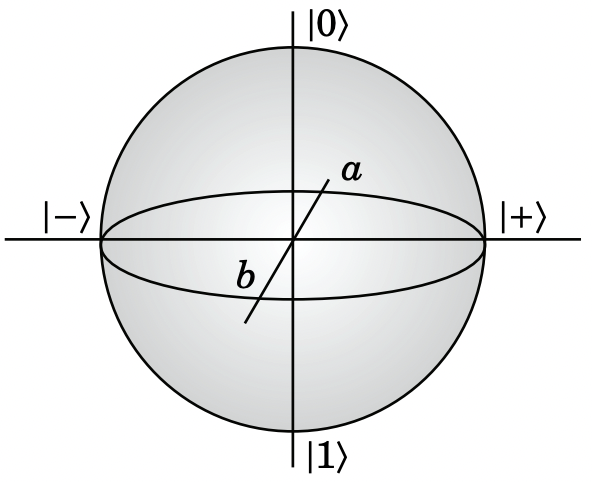
Це називається сферою Блоха, а оператори представлені прямими лініями через початок. Вісь обертання для прямих, що обертаються з часом, визначається гамільтоном. У наведеному вище випадку гамільтоніан був пропорційний\(Z\), а це означає, що прямі лінії обертаються навколо осі через власні\(Z\), які є\(|0\rangle\) і\(|1\rangle\).