2: Постулати квантової механіки

Вся структура квантової механіки (включаючи її релятивістське розширення) може бути сформульована з точки зору станів і операцій в гільбертовому просторі. Нам потрібні правила, які відображають фізичні величини, такі як стани, спостережувані та вимірювання, до математичної структури векторних просторів, векторів та операторів. Існує кілька способів, за допомогою яких це можна зробити, і тут ми узагальнюємо ці правила в плані п'яти постулатів.

Існує ряд важливих аспектів цього постулату. По-перше, той факт, що стани - це промені, а не вектори, означає, що загальна фаза$e^{i \varphi}$ стану не має ніяких фізично спостережуваних наслідків, і$e^{i \varphi}|\psi\rangle$ являє собою той же стан, що і$|\psi\rangle$. По-друге, держава містить всю інформацію про систему. Зокрема, в цій стандартній формулюванні квантової механіки немає прихованих змінних. Нарешті, розмірність$\mathscr{H}$ може бути нескінченною, що має місце, наприклад,$\mathscr{H}$ коли простір інтегровних квадратів функцій.

Як приклад цього постулату розглянемо дворівневу квантову систему (кубіт). Цю систему можна описати двома ортонормальними станами$|0\rangle$ і$|1\rangle$. Завдяки лінійності гільбертового простору суперпозиція знову$\alpha|0\rangle+\beta|1\rangle$ є станом системи, якщо вона має норму 1, або

$$(\alpha ^ { * } \langle0|+\beta^{*}\langle 1|)(\alpha|0\rangle+\beta|1\rangle)=1 \quad \text { or } \quad|\alpha|^{2}+|\beta|^{2}=1\tag{2.1}$$

Це називається принципом суперпозиції: будь-яка нормалізована суперпозиція дійсних квантових станів знову є дійсним квантовим станом. Це прямий наслідок лінійності векторного простору, і, як ми побачимо пізніше, цей принцип має деякі химерні наслідки, які були підтверджені в багатьох експериментах.

Ми використовуємо капелюх, щоб розрізняти спостережуваного і оператора, але зазвичай це розмежування не є необхідним. У цих замітках ми будемо використовувати головні убори тільки тоді, коли є небезпека плутанини.

Як приклад візьмемо оператор$X$:

$$X|0\rangle=|1\rangle \quad \text { and } \quad X|1\rangle=|0\rangle.\tag{2.2}$$

Цей оператор можна інтерпретувати як бітове перевертання кубіта. У матричних позначеннях вектори стану можуть бути записані як

$$|0\rangle=\left(\begin{array}{l}1 \\ 0 \end{array}\right) \quad \text { and } \quad|1\rangle=\left(\begin{array}{l} 0 \\ 1 \end{array}\right),\tag{2.3}$$

що означає,$X$ що написано як

\ [X=\ лівий (\ begin {масив} {ll}
0 & 1\
1 & 0
\ end {масив}\ праворуч)\ tag {2.4}\]

з власними значеннями ±1. Власні стани$X$ є

$$|\pm\rangle=\frac{|0\rangle \pm|1\rangle}{\sqrt{2}}.\tag{2.5}$$

Ці стани утворюють ортонормальну основу.

$A$Очікувана величина по відношенню до стану системи$|\psi\rangle$ позначається$\langle A\rangle$, і оцінюється як

$$\langle A\rangle=\langle\psi|A| \psi\rangle=\langle\psi|(\sum_{j} a_{j}|a_{j}\rangle\langle a_{j}|)| \psi\rangle=\sum_{j} p(a_{j}) a_{j}\tag{2.8}$$

Це середньозважене значення результатів вимірювань. Розкид результатів вимірювань (або невизначеність) задається дисперсією

$$(\Delta A)^{2}=\left\langle(A-\langle A\rangle)^{2}\right\rangle=\left\langle A^{2}\right\rangle-\langle A\rangle^{2}\tag{2.9}$$

Поки ми в основному мали справу з дискретними системами на скінченновимірних гільбертових просторах. Але як щодо безперервних систем, таких як частка в коробці або гармонійний генератор? Ми все ще можемо записати спектральне розкладання оператора A, але суму потрібно замінити інтегралом:

$$A=\int d a f_{A}(a)|a\rangle\langle a|\tag{2.10}$$

де$|a\rangle$ є власним станом$A$. Як правило, виникають проблеми з нормалізацією$|a\rangle$, що пов'язано з неможливістю підготовки системи саме в такому стані$|a\rangle$. Ми не будемо вивчати ці тонкощі далі в цьому курсі, але ви повинні знати, що вони існують. Очікувана$A$ величина

$$\langle A\rangle=\langle\psi|A| \psi\rangle=\int d a f_{A}(a)\langle\psi \mid a\rangle\langle a \mid \psi\rangle \equiv \int d a f_{A}(a)|\psi(a)|^{2},\tag{2.11}$$

де ми визначили хвильову функцію$\psi(a)=\langle a \mid \psi\rangle$, і$|\psi(a)|^{2}$ правильно інтерпретується як щільність ймовірності, яку ви пам'ятаєте з квантової механіки другого року.

Імовірність знаходження власного значення оператора$A$ в інтервалі$a$ та$a+d a$ заданому стані$|\psi\rangle$ дорівнює

$$\langle\psi|(|a\rangle\langle a| d a)| \psi\rangle \equiv d p(a),\tag{2.12}$$

так як обидві сторони повинні бути нескінченно малі. Тому ми вважаємо, що

$$\frac{d p(a)}{d a}=|\psi(a)|^{2}\tag{2.13}$$

Ми можемо записати стан системи в той час$t$ як$|\psi(t)\rangle$, а в якийсь час$t_{0}<t$ як$\left|\psi\left(t_{0}\right)\right\rangle$. Четвертий постулат говорить нам про те, що існує унітарний оператор$U\left(t, t_{0}\right)$, який перетворює державу$t_{0}$ в момент часу в державу$t$:

$$|\psi(t)\rangle=U\left(t, t_{0}\right)\left|\psi\left(t_{0}\right)\right\rangle\tag{2.14}$$

Оскільки еволюція від часу$t$ до$t$ позначається$U(t, t)$ і повинна дорівнювати ідентичності, ми виводимо, що$U$ залежить лише від різниці в часі:$U\left(t, t_{0}\right)=U\left(t-t_{0}\right)$, і$U(0)=\mathbb{I}$.

Як приклад,$U(t)$ нехай генеруються ермітовим оператором$A$ відповідно до

$U(t)=\exp \left(-\frac{i}{\hbar} A t\right)\tag{2.15}$

Аргумент експоненціальної повинен бути безрозмірним, тому$A$ повинен бути пропорційний$\hbar$ раз кутової частоті (іншими словами, енергії). Припустимо, що$|\psi(t)\rangle$ це стан кубіта, і що$A=\hbar \omega X$. Якщо$|\psi(0)\rangle=|0\rangle$ ми хочемо обчислити стан системи на час$t$. Ми можемо написати

$$|\psi(t)\rangle=U(t)|\psi(0)\rangle=\exp (-i \omega t X)|0\rangle=\sum_{n=0}^{\infty} \frac{(-i \omega t)^{n}}{n !} X^{n}\tag{2.16}$$

Зауважте$X^{2}=\mathbb{I}$, що, таким чином, ми можемо розділити ряди степенів на парні та непарні значення n:

$$|\psi(t)\rangle=\sum_{n=0}^{\infty} \frac{(-i \omega t)^{2 n}}{(2 n) !}|0\rangle+\sum_{n=0}^{\infty} \frac{(-i \omega t)^{2 n+1}}{(2 n+1) !} X|0\rangle=\cos (\omega t)|0\rangle-i \sin (\omega t)|1\rangle\tag{2.17}$$

Іншими словами, стан коливається між$|0\rangle$ і$|1\rangle$.

Четвертий постулат також призводить до рівняння Шредінгера. Візьмемо нескінченно малу форму Eq. (2.14):

$$|\psi(t+d t)\rangle=U(d t)|\psi(t)\rangle\tag{2.18}$$

Ми вимагаємо, що$U(d t)$ генерується деяким ермітовим оператором$H$:

$$U(d t)=\exp \left(-\frac{i}{\hbar} H d t\right)\tag{2.19}$$

$H$повинні мати розміри енергії, тому ми ототожнюємо її з енергетичним оператором, або гамільтоном. Тепер ми можемо взяти розширення Тейлора$|\psi(t+d t)\rangle$ до першого порядку в dt:

$$|\psi(t+d t)\rangle=|\psi(t)\rangle+d t \frac{d}{d t}|\psi(t)\rangle+\ldots,\tag{2.20}$$

і ми також розширюємо унітарний оператор до першого порядку в dt:

$$U(d t)=1-\frac{i}{\hbar} H d t+\ldots\tag{2.21}$$

Поєднуємо це в

$$|\psi(t)\rangle+d t \frac{d}{d t}|\psi(t)\rangle=\left(1-\frac{i}{\hbar} H d t\right)|\psi(t)\rangle,\tag{2.22}$$

які можна переробити в рівняння Шредінгера:

$$i \hbar \frac{d}{d t}|\psi(t)\rangle=H|\psi(t)\rangle\tag{2.23}$$ Тому рівняння Шредінгера випливає безпосередньо з постулатів!

Це сумнозвісний постулат проекції, названий так, тому що вимірювання «проектує» систему до власного стану, відповідного вимірюваному значенню. Цей постулат має як помітний наслідок, що друге вимірювання відразу після першого також знайде результат$a_{j}$. Кожен результат вимірювання$a_{j}$ відповідає оператору проекції$P_{j}$ на підпросторі, що охоплюється власним вектором (ами), що належать$a_{j}$. (ідеальне) вимірювання можна описати, застосувавши проектор до стану, і перенормалізувати:

$$|\psi\rangle \rightarrow \frac{P_{j}|\psi\rangle}{\| P_{j}|\psi\rangle \|}\tag{2.24}$$

Це також працює для вироджених власних значень.

Ми встановили раніше, що очікуване значення$A$ можна записати у вигляді сліду:

$$\langle A\rangle=\operatorname{Tr}(|\psi\rangle\langle\psi| A)\tag{2.25}$$

Тепер замість оператора$A$ full обчислюємо слід$P_{j}=\left|a_{j}\right\rangle\left\langle a_{j}\right|$:

$$\left\langle P_{j}\right\rangle=\operatorname{Tr}\left(|\psi\rangle\langle\psi| P_{j}\right)=\operatorname{Tr}\left(|\psi\rangle\left\langle\psi \mid a_{j}\right\rangle\left\langle a_{j}\right|\right)=\left|\left\langle a_{j} \mid \psi\right\rangle\right|^{2}=p\left(a_{j}\right)\tag{2.26}$$

Таким чином, ми можемо обчислити ймовірність результату вимірювання, взявши очікуване значення оператора проекції, яке відповідає власному стану результату вимірювання. Це один з основних розрахунків в квантовій механіці, який ви повинні вміти робити.

Задача вимірювання

Проекційний постулат є дещо проблематичним для інтерпретації квантової механіки, оскільки він призводить до так званої проблеми вимірювання: Чому вимірювання індукує неунітарну еволюцію системи? Зрештою, вимірювальний апарат також може бути описаний квантово механічно ² і тоді система плюс вимірювальний апарат еволюціонує одинично. Але тоді ми повинні викликати новий прилад, який вимірює комбіновану систему та вимірювальний апарат. Однак це в свою чергу можна описати квантово механічно і так далі.

З іншого боку, ми бачимо певні результати вимірювань, коли проводимо експерименти, тому на якомусь рівні проекційний постулат необхідний, і десь повинен бути «колапс хвильової функції». Шредінгер вже боровся з цим питанням, і придумав свій знаменитий думковий експеримент про кота в коробці з наповненим отрутою флаконом, прикріпленим до лічильника Гейгера, що контролює радіоактивний атом (рис. 1). Коли атом розпадається, він спрацьовує лічильник Гейгера, що, в свою чергу, викликає викид отрути, що вбиває кота. Коли ми не заглядаємо всередину коробки (точніше: коли з коробки не вислизає жодна інформація про систему атом-контр-флакон-кішка), вся система знаходиться в квантовій суперпозиції. Однак, коли ми відкриваємо коробку, ми знаходимо кота або мертвим, або живим. Одне з рішень проблеми, здається, полягає в тому, що квантовий стан представляє наші знання про систему, і що, дивлячись всередину коробки, просто оновлює нашу інформацію про атом, лічильник, флакон і кішку. Так що нічого не «руйнується», крім нашого власного душевного стану.

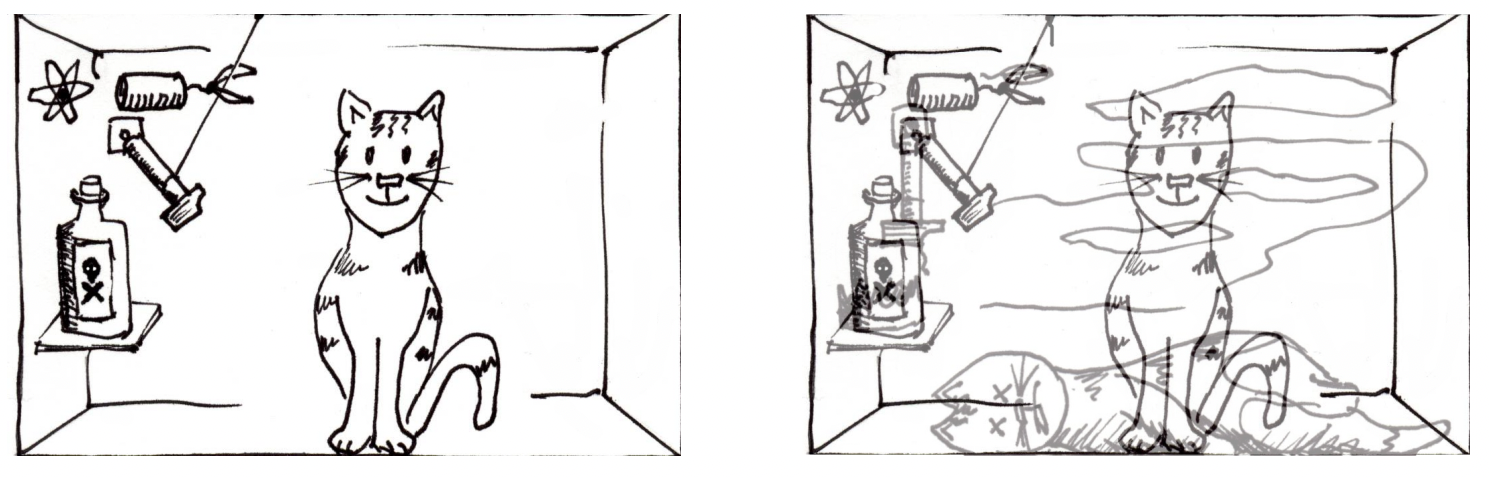Малюнок 1: Кіт Шредінгера.

Однак це не може бути цілою історією, тому що квантова механіка явно стосується не лише нашої думки про котів та розкладаються атоми. Зокрема, якщо ми підготуємо електрон у стані «вгору»$|\uparrow\rangle$, то щоразу, коли ми вимірюємо спін вздовж$z$ -напрямку, ми знайдемо результат вимірювання «вгору», незалежно від того, що ми думаємо про електрони та квантову механіку. Так що, здається, є якась фізична властивість, пов'язана з електроном, яке визначає результат вимірювання і описується квантовим станом.

Різні інтерпретації квантової механіки намагаються вирішити ці (та інші) питання. Оригінальна інтерпретація квантової механіки була в основному висунута Нільсом Бором, і називається Копенгагенської інтерпретацією. Загалом, це говорить про те, що квантовий стан - це зручна художня література, яка використовується для обчислення результатів вимірювань, і що систему не можна вважати окремою від вимірювального апарату. Крім того, існують інтерпретації квантової механіки, такі як інтерпретація Гірарді-Ріміні-Вебера, які приписують якусь реальність стану системи, і в цьому випадку повинен бути наведений фізичний механізм колапсу хвильової функції. Багато з цих інтерпретацій можна класифікувати як приховані теорії змінних, які постулюють, що існує більш глибока фізична реальність, описана деякими «прихованими змінними», які ми повинні усереднити. Це, в свою чергу, пояснює ймовірнісний характер квантової механіки. Проблема таких теорій полягає в тому, що ці приховані змінні повинні бути досить дивними: вони можуть миттєво змінюватися залежно від подій світлових років3, порушуючи тим самим теорію особливої відносності Ейнштейна. Багатьом фізикам не подобається цей аспект прихованих змінних теорій.

Крім того, квантову механіку можна інтерпретувати з точки зору «багатьох світів»: інтерпретація Багато світів стверджує, що існує один вектор стану для всього Всесвіту, і що кожне вимірювання розбиває Всесвіт на різні гілки, що відповідають різним результатам вимірювань. Це привабливо, оскільки здається філософськи послідовною інтерпретацією, і хоча вона набуває все більшої кількості прихильників протягом останніх років ⁴, багато фізиків мають глибоку відраза до ідеї паралельних всесвітів.

Нарешті, існує епістемічна інтерпретація, яка дуже схожа на Копенгагенську інтерпретацію в тому, що вона розглядає квантовий стан значною мірою як міра наших знань про квантову систему (і вимірювальний апарат). У той же час він заперечує глибшу базову реальність (тобто відсутність прихованих змінних). Привабливою особливістю цієї інтерпретації є те, що вона вимагає мінімальної кількості суєти і природно вписується в сучасні дослідження квантової теорії інформації. Мінусом є те, що доводиться відмовитися від простого наукового реалізму, що дозволяє говорити про властивості електронів і фотонів, і багато фізики не готові до цього робити.

Як бачите, квантова механіка змушує нас відмовитися від деяких глибоко вкорінених (класичних) переконань про Природу. Залежно від ваших уподобань, вас можуть тягнути до тієї чи іншої інтерпретації. В даний час не відомо, яке тлумачення є правильним.

Вправи

1. Обчисліть власні значення та власні стани оператора бітового$X$ фліпа, і показати, що власні стани утворюють ортонормальну основу. Обчисліть очікуване значення$X$ для$|\psi\rangle=1 / \sqrt{3}|0\rangle+i \sqrt{2 / 3}|1\rangle$.
2. Показати, що дисперсія$A$$|\psi\rangle$ зникає, коли є власним станом$A$.
3. Доведіть, що оператор Ермітіана, якщо і тільки якщо він має реальні власні значення.
4. Показати, що кубіт у невідомому стані$|\psi\rangle$ неможливо скопіювати. Це теорема про відсутність клонування. Підказка: почніть зі стану$|\psi\rangle|i\rangle$ для якогось початкового стану$|i\rangle$, і вимагайте, щоб для$|\psi\rangle=|0\rangle$ і$|\psi\rangle=|1\rangle$ процедура клонування була унітарною трансформацією$|0\rangle|i\rangle \rightarrow|0\rangle|0\rangle$ і$|1\rangle|i\rangle \rightarrow|1\rangle|1\rangle$.
5. Принцип невизначеності.
   1. Використовуйте нерівність Коші-Шварца, щоб отримати наступне співвідношення між спостережуваними, що не комутуються,$A$ і$B$:

      $$(\Delta A)^{2}(\Delta B)^{2} \geq \frac{1}{4}|\langle[A, B]\rangle|^{2}\tag{2.27}$$

      Підказка: визначте$|f\rangle=(A-\langle A\rangle)|\psi\rangle$ і$|g\rangle=i(B-\langle B\rangle)|\psi\rangle$, і використовуйте це$|\langle f \mid g\rangle| \geq \frac{1}{2} \mid\langle f \mid g\rangle+\langle g|f\rangle|$.

   2. Покажіть, що це зводиться до співвідношення невизначеності Гейзенберга, коли$A$ і$B$ є канонічно сполученими спостережуваними, наприклад, позицією та імпульсом.
   3. Чи працює цей метод для виведення принципу невизначеності між енергією та часом?
6. Розглянемо гамільтоніан$H$ і стан,$|\psi\rangle$ дане

   \ [H = E\ лівий (\ почати {масив} {ccc}
   0 & я & 0\\
   -i & 0\\ 0 &
   0 & 0 & 0 & -1
   \ кінець {масив}\ праворуч)\ квад\ текст {і}\ quad|\ psi\ rangle=\ frac {1} {\ sqrt {5}}\ ліворуч (\ почати {масив} {c}
   
   1-i \\
   1
   \ end {масив}\ право)\ tag {2.28}\]

   де$E$ - константа з розмірами енергії. Обчисліть енергетичні власні значення і очікуване значення гамільтоніана.

7. Покажіть, що імпульс і сумарна енергія можна виміряти одночасно тільки тоді, коли потенціал всюди постійний. Що означає постійний потенціал з точки зору динаміки частинки?

---

¹ У гільбертових просторах нескінченної розмірності існують тонкі відмінності між самоспряженими та ермітовими операторами. Ми ігноруємо ці тонкощі тут, тому що ми будемо мати справу в основному з скінченновимірними просторами.

² Це те, чого більшість людей вимагають від фундаментальної теорії: квантова механіка не повинна просто руйнуватися для макроскопічних об'єктів. Дійсно, експериментальні докази макроскопічних суперпозицій були знайдені у вигляді «котячих станів».

³., навіть якщо усереднення над прихованими змінними означає, що ви ніколи не можете сигналізувати швидше, ніж світло.

⁴ Здається, є деякі докази того, що інтерпретація «Багато світів» добре поєднується з останніми космологічними моделями, заснованими на теорії струн.