4.2: Квадратний потенційний бар'єр
- Page ID
- 76895
Розглянемо частинку маси\(m\) і енергії, що\(E>0\) взаємодіють з простим квадратним потенційним бар'єром
\ begin {рівняння} V (x) =\ left\ {\ begin {масив} {ll}
V_ {0} &\ text {для} 0\ leq x\ leq a\\
0 &\ text {інакше}
\ end {масив}\ справа. \ end {рівняння}
де\(V_0>0\). У областях ліворуч і праворуч від бар'єру,\(\psi(x)\) задовольняє, \[\label{e5.15} \frac{d^{\,2} \psi}{d x^{\,2}} = - k^{\,2}\,\psi,\]де\(k\) задано рівнянням ([e5.6]).
Приймемо наступне рішення попереднього рівняння зліва від бар'єру (тобто\(x<0\)):\[\psi(x) = {\rm e}^{\,{\rm i}\,k\,x} + R\,{\rm e}^{-{\rm i}\,k\,x}.\] Це рішення складається з плоскої хвилі одиничної амплітуди, що рухається вправо [оскільки залежна від часу хвильова функція множиться на\(\exp(-{\rm i}\,\omega\,t)\), де\(\omega=E/\hbar>0\)], і a плоска хвиля складної амплітуди\(R\) рухається вліво. Першу плоску хвилю ми інтерпретуємо як вхідну частку (а точніше, потік вхідних частинок), а другу як частинку (або потік частинок), відбиту потенційним бар'єром. Звідси і\(|R|^{\,2}\) є ймовірність роздумів. У цьому можна переконатися, обчисливши струм ймовірності ([eprobc]) в області\(x<0\), який набуває вигляду,\[j_l=v\,(1-|R|^{\,2}),\] де\(v = p/m=\hbar\,k/m\) знаходиться класична швидкість частинок.
Приймемо наступне рішення рівняння ([e5.15]) праворуч від бар'єру (тобто\(x>a\)):\[\psi(x) = T\,{\rm e}^{\,{\rm i}\,k\,x}.\] Це рішення складається з плоскої хвилі складної амплітуди, що\(T\) рухається вправо. Ми інтерпретуємо це як частинку (або потік частинок), що передається через бар'єр. Звідси і\(|T|^{\,2}\) є ймовірність передачі. Струм ймовірності в області\(x>a\) набуває вигляду\[j_r = v\, |T|^{\,2}.\] Now, згідно Equation ([ediffp]), в стаціонарному стані (тобто\(\partial |\psi|^{\,2}/\partial t = 0\)) струм ймовірності є просторовою константою (тобто\(\partial j/\partial x = 0\)). Отже, ми повинні мати\(j_l=j_r\), або \[\label{e5.20} |R|^{\,2} + |T|^{\,2} = 1.\]Іншими словами, ймовірності відображення та передачі суми до одиниці, як це повинно бути, оскільки відображення та передача є єдиними можливими наслідками для частинки, що падає на бар'єр.
Усередині бар'єру (тобто\(0\leq x \leq a\)),\(\psi(x)\) задовольняє \[\label{e5.21} \frac{d^{\,2} \psi}{d x^{\,2}} = - q^{\,2}\,\psi,\]де\[q^{\,2} = \frac{2\,m\,(E-V_0)}{\hbar^{\,2}}.\]
Розглянемо, перш за все, випадок де\(E> V_0\). У цьому випадку загальне рішення рівняння ([e5.21]) всередині бар'єру набуває вигляду\[\psi(x) = A\,{\rm e}^{\,{\rm i}\,q\,x} +B\,{\rm e}^{-{\rm i}\,q\,x},\] де\(q=\sqrt{2\,m\,(E-V_0)/\hbar^{\,2}}\).
Тепер граничні умови на краях бар'єру (тобто в\(x=0\) і\(x=a\)) є такими\(\psi\) і\(d\psi/d x\) є суцільними. Ці граничні умови гарантують, що струм ймовірності ([eprobc]) залишається скінченним і безперервним по краях кордону, як це повинно бути, якщо він повинен бути просторовою константою.
Неперервність\(\psi\) і\(d\psi/d x\) на лівому краю бар'єру (тобто\(x=0\)) дає\[\begin{aligned} 1 + R &= A+B,\\[0.5ex] k\,(1-R) &= q\,(A-B).\end{aligned}\] Аналогічно, безперервність\(\psi\) і\(d\psi/d x\) на правому краю бар'єру (тобто\(x=a\)) дає\[\begin{aligned} A\, {\rm e}^{\,{\rm i}\,q\,a}+ B \,{\rm e}^{-{\rm i}\,q\,a} &= T\,{\rm e}^{\,{\rm i}\,k\,a},\\[0.5ex] q\left(A\,{\rm e}^{\,{\rm i}\,q\,a} -B \,{\rm e}^{-{\rm i}\,q\,a}\right) &=k\,T\,{\rm e}^{\,{\rm i}\,k\,a}.\end{aligned}\] Після значної алгебри попередні чотири рівняння дають \[\label{e5.28} |R|^{\,2} = \frac{(k^{\,2}-q^{\,2})^{\,2}\,\sin^2(q\,a)}{4\,k^{\,2}\,q^{\,2} + (k^{\,2}-q^{\,2})^{\,2}\,\sin^2(q\,a)},\]і \[\label{e5.29} |T|^{\,2} = \frac{4\,k^{\,2}\,q^{\,2}}{4\,k^{\,2}\,q^{\,2} + (k^{\,2}-q^{\,2})^{\,2}\,\sin^2(q\,a)}.\]Зверніть увагу, що попередні два вирази задовольняють обмеженню ([e5.20]).
Повчально порівнювати квантові механічні ймовірності відбиття та передачі - ([e5.28]) та ([e5.29]) відповідно - з тими, що походять з класичної фізики. Тепер, згідно з класичною фізикою, якщо частинка енергії\(E\) падає на потенційний бар'єр висоти,\(V_0<E\) то частинка сповільнюється при проходженні через бар'єр, але в іншому випадку не впливає. Іншими словами, класична ймовірність відображення дорівнює нулю, а класична ймовірність передачі - одиниця.
Малюнок 10: Вірогідності передачі (твердої кривої) та відбиття (штрихової кривої) для квадратного потенційного бар'єру ширини\(\begin{equation}a=1.25 \lambda\end{equation}\), де\(\lambda\) довжина хвилі вільного простору де Броля, як функція співвідношення висоти бар'єру, \(\begin{equation}V_{0}\end{equation}\), до енергії\(\begin{equation}E\end{equation}\), падаючої частинки.
Малюнок 11: Передача (тверда крива) і відбиття (штрихова крива) ймовірності для частинки енергії
\(\begin{equation}V_{0}=0.75 E\end{equation}\), що падає на квадратний потенційний бар'єр висоти, як функція відношення ширини бар'єру\(\begin{equation}a\end{equation}\), до вільного -простір довжини хвилі Броля,\(\lambda\)
Імовірності відображення і передачі, отримані з рівнянь ([e5.28]) і ([e5.29]) відповідно, побудовані на малюнках [fb1] і [fb2]. З малюнка [fb1] видно, що класичний результат,\(|R|^{\,2}=0\) причому\(|T|^{\,2}=1\), виходить в тій межі, де висота бар'єру відносно невелика (тобто\(V_0\ll E\)). Однак, коли\(V_0\) в порядку\(E\), існує істотна ймовірність того, що падаюча частинка буде відображена бар'єром. Відповідно до класичної фізики, рефлексія неможлива при\(V_0 < E\).
Також видно, з малюнка [fb2], що при певних ширині бар'єру ймовірність відображення йде до нуля. Виявляється, це вірно незалежно від енергії падаючої частинки. З Equation ([e5.28]) видно, що ці спеціальні ширини бар'єру відповідають\[q\,a = n\,\pi,\] де\(n=1,2,3,\cdots\). Іншими словами, ширина спеціальних бар'єрів є цілими числами кратними половині довжини хвилі де Броля частинки всередині бар'єру. Відбиття на спеціальній ширині бар'єру немає, оскільки при цих ширині зворотна бігова хвиля, відбита від лівого краю бар'єру, руйнівно заважає подібній хвилі, відбитій від правого краю бар'єру, щоб дати нульову чисту відбиту хвилю.
Давайте тепер розглянемо випадок\(E< V_0\). У цьому випадку загальне рішення рівняння ([e5.21]) всередині бар'єру набуває вигляду\[\psi(x) = A\,{\rm e}^{\,q\,x} + B\,{\rm e}^{-q\,x},\] де\(q=\sqrt{2\,m\,(V_0-E)/\hbar^{\,2}}\). Неперервність\(\psi\) і\(d \psi/d x\) на лівому краю бар'єру (тобто\(x=0\)) дає\[\begin{aligned} 1 + R &=A+B,\\[0.5ex] {\rm i}\,k\,(1-R) &= q\,(A-B).\end{aligned}\] Аналогічно, безперервність\(\psi\) і\(d\psi/d x\) на правому краю бар'єру (тобто\(x=a\)) дає\[\begin{aligned} A\, {\rm e}^{\,q\,a}+ B \,{\rm e}^{-q\,a} &= T\,{\rm e}^{\,{\rm i}\,k\,a},\\[0.5ex] q\left(A\, {\rm e}^{\,q\,a}-B \,{\rm e}^{-q\,a}\right) &= {\rm i}\,k\,T\,{\rm e}^{\,{\rm i}\,k\,a}.\end{aligned}\] Після значної алгебри попередні чотири Рівняння вихід \[\label{e5.36} |R|^{\,2} = \frac{(k^{\,2}+q^{\,2})^{\,2}\,\sinh^2(q\,a)}{4\,k^{\,2}\,q^{\,2} + (k^{\,2}+q^{\,2})^{\,2}\,\sinh^2(q\,a)},\]і \[\label{e5.37} |T|^{\,2} = \frac{4\,k^{\,2}\,q^{\,2}}{4\,k^{\,2}\,q^{\,2} + (k^{\,2}+q^{\,2})^{\,2}\,\sinh^2(q\,a)}.\]Ці вирази також можуть бути отримані з Рівняння ([e5.28]) і ([e5.29]) шляхом підстановки\(q\rightarrow -{\rm i}\,q\). Зверніть увагу, що рівняння ([e5.36]) і ([e5.37]) задовольняють обмеженню ([e5.20]).
Знову повчально порівнювати квантові механічні ймовірності відбиття та транс-місії— ([e5.36]) та ([e5.37]) відповідно - з тими, що походять з класичної фізики. Тепер, згідно з класичною фізикою, якщо частинка енергії\(E\) падає на потенційний бар'єр висоти,\(V_0>E\) то частинка відбивається. Іншими словами, класична ймовірність відображення - це одиниця, а класична ймовірність передачі дорівнює нулю.
Малюнок 12: Вірогідності передачі (твердої кривої) та відбиття (штрихової кривої) для квадратного потенційного бар'єру ширини\(\begin{equation}a=0.5 \lambda \text { , where } \lambda \text { is }\end{equation}\) хвилі вільного простору де Броля, як функція відношення енергії, вхідної частинки до висоти, \(\begin{equation}V_{0}\end{equation}\), бар'єру.
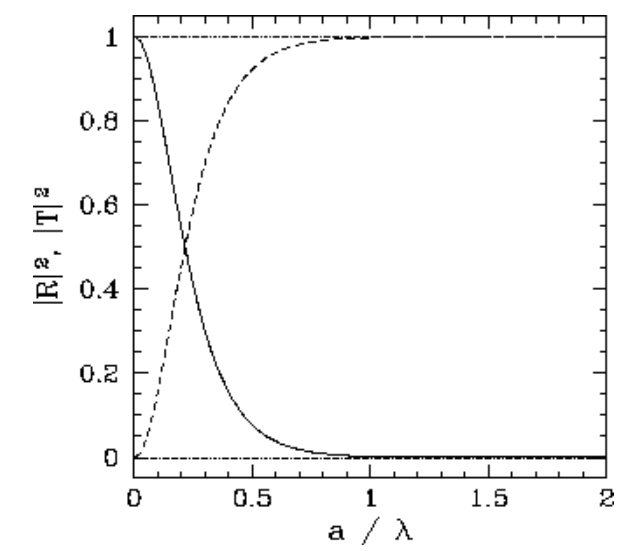
Малюнок 13: Вірогідності передачі (тверда крива) та відбиття (штрихова крива) для частинки енергії\(\begin{equation}V_{0}=(4 / 3) E\end{equation}\), що падає на квадратний потенційний бар'єр висоти, як функція відношення ширини бар'єру
, до вільного простору де Довжина хвилі Broglie,\(\lambda\)
Імовірності відображення і передачі, отримані з Рівнянь ([e5.36]) і ([e5.37]), відповідно, побудовані на малюнках [fb3] і [fb4]. З малюнка [fb3] видно, що класичний результат,\(|R|^{\,2}=1\) причому\(|T|^{\,2}=0\), виходить для відносно тонких бар'єрів (тобто\(q\,a\sim 1\)) в тій межі, де висота бар'єру відносно велика (тобто\(V_0\gg E\)). Однак, коли\(V_0\) в порядку\(E\), існує істотна ймовірність того, що падаюча частинка буде передаватися бар'єром. Згідно з класичною фізикою, передача неможлива при\(V_0 > E\).
З малюнка [fb4] видно також, що ймовірність передачі зменшується експоненціально з збільшенням ширини бар'єру. Проте навіть для дуже широких бар'єрів (тобто\(q\,a\gg 1\)) існує невелика, але кінцева ймовірність того, що частка, що падає на бар'єр, буде передаватися. Це явище, незрозуміле в контексті класичної фізики, називається тунелюванням.