8.1: Обертові рамки відліку
- Page ID
- 77254
Цілі навчання
- Поясніть систему координат обертання та обертання
Немає синхронізації годин
Панелі 1 та 2 малюнка\(\PageIndex{1}\) повторюють результат Прикладу 1.4.6. Набір з трьох годинників, закріплених на землі в\(\PageIndex{1}\) (1), були синхронізовані за допомогою синхронізації Ейнштейна (приклад 1.1.4), тобто шляхом обміну спалахами світла. Три годинники на борту рухомого поїзда\(\PageIndex{1}\) (2) були синхронізовані таким же чином, а події, які були одночасними відповідно до кадру 1, не є одночасними у кадрі 2. Відбувається систематичний зсув часу, який представлений терміном\(t' = ... - vγx\) в перетворенні Лоренца (Рівняння 1.4.1).
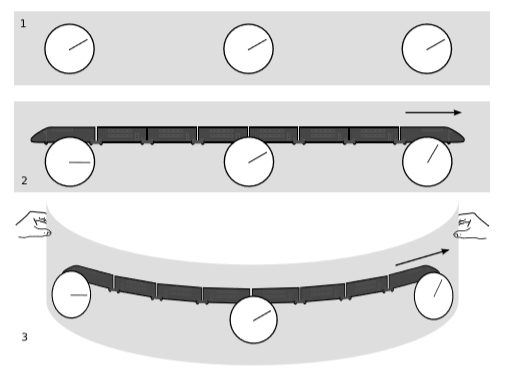
Тепер припустимо, ми беремо схему поїзда і обертаємо її навколо,\(\PageIndex{1}\) (3). Якщо ми продовжимо і замкнемо петлю, зробивши ланцюжок в коло, як кольє ланцюжка, у нас проблема. Тенденція часу годинника може тривати, поки вона не обернеться назад до початку, але тоді буде невідповідність.
Зроблено висновок, що годинник не можуть бути синхронізовані в обертовій системі відліку. Такий кадр не допускає універсальної часової координати, оскільки синхронізація Ейнштейна не є перехідною: синхронізація годинника A з годинником B, а B з C, не означає, що A синхронізується з C. Ця неперехідність є одним із способів визначення того, що ми маємо на увазі під обертанням. Тобто, якщо оперативне визначення інерційного кадру, наведене в розділі 5.1, показує, що наш кадр неінерційний, і ми хочемо дізнатися більше про те, чому він неінерційний, тестування на цю неперехідність - це спосіб з'ясувати, чи це через обертання.
Обертання локально визначається
Люди на борту кругового поїзда знають, що їхні спроби синхронізації зазнають невдачі, тому вони можуть сказати, без прив'язки до чогось зовнішнього, що вони йдуть по колу.
Хоча це книга про особливу, а не загальну, відносності, цікаво відзначити наступну можливість. Припустимо, що ми перевіряємо шляхом локальних експериментів, що у нас є хороша, необертається, інерційна система відліку. Тоді можна уявити, що якщо ми розглянемо далекі галактики з цього кадру, ми побачимо, як вони обертаються з деякою кутовою частотою\(Ω\) навколо якоїсь осі на небесній сфері. Якщо це спостерігається, то ми повинні зробити висновок, що це Всесвіт в цілому, а не наша лабораторія! — тобто обертається. Такий ефект шукали, і, наприклад, верхня межа\(\Omega \lesssim 10^{-7}\) радіан/рік була виведена Клеменсом. 1 Загально-релятивістські моделі таких обертових космологій мають кращий вектор, що становить напрямок осі, навколо якої матерія обертається, але глобального центру обертання немає. Поточні\(Ω\) верхні межі на досить хороші, щоб виключити будь-який істотний вплив на космологічне розширення за рахунок відцентрових сил.
Ефект Саньяка
Хоча сценарій поїзда, очевидно, нереальний, часовий зсув далеко не гіпотетичний. Цей тип ефекту, званий ефектом Саньяка, вперше спостерігав М.Жорж Саньяк в 1913 році, і він відноситься до принципу кільцевого лазерного гіроскопа (приклад 1.1.4), використовуваного в пасажирських струменях. (Назва французька, і вимовляється\ Сах-няхк.») Щоб кількісно знайти ефект Саньяка, відзначимо, що в прикладі кругового поїзда (ігноруючи знаки) відповідний термін у перетворенні Лоренца\(v\gamma x\), накопичило б після однієї повної схеми синхронізації Ейнштейна невідповідність,\(\delta\) рівну окружності кола множиться на\(v\gamma\). Якщо радіус кола\(r\) і кутова швидкість\(\omega\), ми маємо\(\Delta t = 2\pi \gamma r^2\omega\). Це може бути переписано з точки зору площі кола\(A\) як\(\Delta t = 2A\omega\), або, повторно вставляючи фактори\(c\) для розміщення одиниць СІ,\(\Delta t = \frac{2A\omega }{c^2}\). Пропорційність закритій площі не випадковість; продукт\(vx\) має форму цілісного,\(F\cdot ds\) що відбувається в теоремі Стокса.
Приклад\(\PageIndex{1}\): Sagnac effect in the Hafele-Keating experiment
Годинник на екваторі землі обертається\(ω\) з частотою\(2π\) радіанів в сидеричний день, страждаючи ефектом Sagnac\(210\: ns\) в день. Подорожуючі атомні годинники в експерименті Хафела-Кітінга обійшли світ в обох напрямках і порівнювалися з третім набором годинників, які залишилися у Вашингтоні, округ Колумбія. Оскільки час, необхідний для польоту навколо землі, також був на порядку одного дня, відмінності у значеннях\(ω\) для трьох наборів годин були на тому ж порядку, що і землі, і тому ми очікуємо кумулятивних\(ω\) диференціальних ефектів Sagnac, які також знаходяться на порядку. сто нано секунд. Ці ефекти існують лише у обертовому кадрі землі, але вимірювані речі належні часи, а належний час є скалярним, тому експериментальні результати не залежать від того, яка система відліку використовується для їх обчислення. Оскільки пілоти авіакомпанії надавали Hafele та Keating навігаційні дані, що стосуються обертової землі, вони проаналізували свої результати в обертовій рамці, в якій був ефект Sagnac. Вони могли б однаково добре перетворити свої дані в кадр зірок, і в цьому випадку був би передбачений той самий результат, але він був би описаний як випливає з кінематичного розширення часу.
Приклад\(\PageIndex{2}\): Ring laser gyroscope
Кільцевий лазерний гіроскоп на фото в прикладі 1.1.4 виглядає так, ніби він має площу на порядку\(10^2\: cm^2\) і використовує червоне світло. Для використання в навігації, людина хоче мати можливість виявити зміни в курсі, скажімо, одного ступеня в нашу годину, або\(ω ∼5×10^{-6}\: radian/s\). Результатом є зсув часу\(∆t ∼ 10^{-24}\: s\), який для червоного світла є фазовим зсувом тільки\(∆φ = 4πAω/cλ ∼3×10^{-9}\) радіан. У оригінальних експериментах дев'ятнадцятого століття цей фазовий зсув повинен був бути виміряний шляхом створення перешкод між двома променями та вимірювання зміни інтенсивності, що виникає внаслідок цієї зміни фази. Наша оцінка\(φ\) показує, що це недоцільно для портативного інструменту. У сучасному кільцевому лазерному гіроскопі в петлю вставляється активне лазерне середовище, і в результаті петля резонує на частоті, яка зрушена від власної частоти лазера на\(∆f ∼ ∆φc/L\), де\(L\) знаходиться окружність. Результатом є зсув частоти на кілька Гц, який легко виміряти. Альтернативна техніка, яка використовується в волоконно-оптичному гіроскопі, полягає в обертанні\(N\) витків оптичного волокна по колу, ефективно\(A\) змінюючись на\(NA\).
Обертається система координат
Система GPS є практичним прикладом випадку, коли ми, природно, хочемо використовувати обертову систему координат. Туристи і моряки, врешті-решт, хочуть знати, де вони знаходяться щодо земної обертової поверхні. Оскільки місця потрібно визначати з точністю до метрів, час сигналів потрібно робити з точністю до чогось подібного\((1 m)/c\), що становить кілька наносекунд. Ось чому супутники GPS мають атомні годинники на борту, і час до цієї точності явно вимагає врахування релятивістських ефектів. Тому нам потрібна не обертова ньютонівська система координат, а обертається релятивістська. Почнемо з кадру, що не обертається, і визначимо координати\((t,r,θ,z)\), причому просторовою частиною\((r,θ,z)\) є звичайні циліндричні координати. Для простоти ми нехтуємо\(z\) координатою в наступному. Розширюючи результат задачі Q1 в главі 7 від\(2 + 0\) вимірів до\(2 + 1\), ми маємо метрику
\[ds^2 = dt^2 - dr^2 - r^2 d\theta ^2\]
Наведені вище результати показують, що ми не очікуємо, що зможемо визначити цілком задовільну часову координату в обертовому кадрі, тому давайте почнемо з мінімальної зміни\((t,r,θ) → (t,r,θ')\), де\(θ' = θ - ωt\). Цього, принаймні, достатньо, щоб світові лінії постійних\(θ'\) були тими, які обертаються навколо походження з відповідною частотою. Підставляючи\(dθ = dθ' + ω dt\), знаходимо
\[ds^2 = (1 - \omega ^2r^2)dt^2 - dr^2 - r^2 d\theta '^2 - 2\omega r^2 d\theta 'dt\]
Визнаючи\(ωr\) як швидкість одного кадру відносно іншого, і\((1 - ω^2r^2) {-1/2}\) як\(γ\), ми бачимо, що у нас є ефект релятивістського розширення часу в\(dt^2\) терміні. Але\(dr^2\) і\(dθ'^2\) терміни виглядають так само, як і в Рівняння\(\PageIndex{1}\). Чому ми не бачимо жодного стиснення Лоренца шкали довжини в азимутальному напрямку?
Відповідь полягає в тому, що координати в відносності є довільними, і тільки тому, що ми можемо записати певний набір координат, це не означає, що вони мають спеціальну фізичну інтерпретацію. Координати фізично\((t,r,θ')\) не відповідають величинам, які обертається спостерігач\(R\) вимірював би за допомогою годинників та метрових паличок. Якщо\(R\) використовується лінійка для вимірювання короткої дуги уздовж окружності кола\(r = r'\), відстань - це відстань, яка вимірюється між подіями в просторові/часі, які є одночасними в іншому кадрі лінійки, і вони не відбуваються в часовому значенні координати часу\(t\). У перетворенні Лоренца, для лінійного руху, це\(-vγx\) термін, застосований до часу, який виправляє ці проблеми і змушує t0 належним чином представляти одночасність у новому кадрі. У нашій обертальної версії ми могли б спробувати зробити щось подібне, визначаючи часову координату\(t' = t + fθ'\), де\(f\) є функція,\(r\) яка розроблена таким чином, що\(dθ'dt\) перехресний термін в метриці буде йти. Це можна зробити (функція\(f\), яка працює, виявляється\(ωr^2/(1 - ω^2r^2)\)), але проблема полягає в тому, що\(t'\) координата не є однозначною, в тому сенсі, що\((t,r,θ)\) і не\((t,r,θ + 2π)\) буде виробляти те ж саме\(t'\). Це неминуче, як ми бачили на початку цього розділу, тому ми не можемо покращити координати\((t,r,θ')\) та метрику (рівняння\(\PageIndex{2}\)).
\((t,r,θ')\)Координати з метрикою (Рівняння\(\PageIndex{2}\)) - це ті, що використовуються в системі GPS, і в цьому контексті називаються координатами з центром Землі (ECI). (Інша назва - координати Born.) Їх часова координата - це не час, виміряний годинником у обертовому кадрі, а просто часова координата необертається системи відліку, прив'язаної до центру землі. Концептуально ми можемо уявити цю часову координату як таку, яка встановлюється шляхом надсилання електромагнітного сигналу «тік-так» з центру землі, при цьому кожен супутник коригує фазу сигналу на основі часу поширення, виведеного з його власного\(r\). Насправді це досягається шляхом зв'язку з головною станцією управління в Колорадо-Спрінгс, яка спілкується з супутниками через реле на Кваджалейн, Острів Вознесіння, Дієго-Гарсія та мисі Канаверал.
