Skip to main content
LibreTexts - Ukrayinska

13.3: Сектори

  1. Last updated
  2. Save as PDF
  • Page ID
    77910

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    На малюнку XIII.2 показана частина еліптичної (або іншого конічного перерізу) орбіти, і вона показує радіуси векторів положення планети в моменти часу\(t_1, \ t_2\) і\(t_3\).

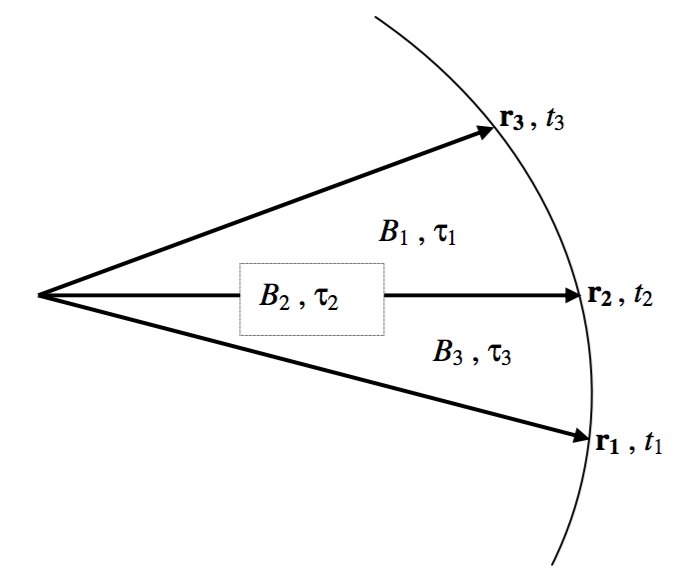
    Малюнок 13.2.png
    \(\text{FIGURE XIII.2}\)

    Позначення, яке я збираюся використовувати, виглядає наступним чином:

    • Площа сектора, утвореного з'єднанням кінчиків орбіти\(\textbf{r}_2\) і\(\textbf{r}_3\) навколо неї, становить\(B_1\).
    • Площа сектора, утвореного з'єднанням кінчиків орбіти\(\textbf{r}_3\) і\(\textbf{r}_1\) навколо неї, становить\(B_2\).
    • Площа сектора, утвореного з'єднанням кінчиків орбіти\(\textbf{r}_1\) і\(\textbf{r}_2\) навколо неї, становить\(B_3\).
    • Часовий інтервал\(t_3 − t_2\) дорівнює\(τ_1\).
    • Часовий інтервал\(t_3 − t_1\) дорівнює\(τ_2\).
    • Часовий інтервал\(t_2 − t_1\) дорівнює\(τ_3\).

    За умови, що дуга досить мала, то до хорошого наближення (іншими словами ми можемо наблизити сектори трикутниками), ми маємо

    \[B_2 \textbf{r}_2 \approx B_1 \textbf{r}_1 + B_3 \textbf{r}_3 . \label{13.3.1} \]

    Тобто,

    \[\textbf{r}_2 \approx b_1 \textbf{r}_1 + b_3 \textbf{r}_3 , \label{13.3.2} \]

    де

    \[b_1 = B_1/B_2 \label{13.3.3} \]

    і

    \[b_3 = B_3 / B_2 \label{13.3.4} \]

    Коефіцієнти\(b_1\) і\(b_3\) є секторними коефіцієнтами, а коефіцієнти\(a_1\) і\(a_3\) є коефіцієнтами трикутника.

    За другим законом Кеплера площі секторів пропорційні часовим інтервалам.

    Тобто\[b_1 = τ_1 / τ_2 \label{13.3.5} \]

    і\[b_3 = τ_3 / τ_2 . \label{13.3.6} \]

    Таким чином, відомі коефіцієнти в Equation\ ref {13.3.2}. Наша мета полягає в тому, щоб використати це наближене рівняння, щоб знайти приблизні значення геліоцентричних відстаней у моменти трьох спостережень, а потім уточнити їх, щоб задовольнити точне рівняння 13.2.5. Ми почнемо нашу спробу зробити це в розділі 13.6, але спочатку слід розглянути наступні три розділи.