Skip to main content
LibreTexts - Ukrayinska

6.9: Довжина року

  1. Last updated
  2. Save as PDF
  • Page ID
    78048

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Час, необхідний для того, щоб Земля оберталася навколо Сонця щодо зірок, що є тим самим, що і час, необхідний для того, щоб Видатне Сонце рухатись навколо екліптики щодо зірок, є сидеричним роком\(365^{\text{d}} .25636\), тобто, де «d» позначає середній сонячний день. Тривалість сезонів, однак, визначається рухом Явного Сонця щодо\(\Upsilon\). Оскільки\(\Upsilon\) рухається на захід уздовж екліптики, час, який Видатне Сонце займає для переміщення навколо екліптики щодо\(\Upsilon\), яка називається Тропічним роком, трохи менше, ніж сидеричний рік. Однак ми бачили, що рух\(\Upsilon\) уздовж екліптики не зовсім рівномірний, і ми повинні усереднити наслідки нутації. Таким чином, Середній тропічний рік - це середній час екліптичної довготи видимого Сонця, щоб збільшити на\(360^\circ\), що є\(365^\text{d} .24219\).

    Календар, який ми використовуємо в повсякденному житті, - це григоріанський календар, в якому існує 365 днів у більшості років, але 366 днів у роках, які діляться на 4, якщо вони також не діляться на 100, крім тих, які також діляться на 400. Таким чином, високосні роки (ті, що мають 366 днів) включають 1996, 2000, 2004, але не 2005 або 1900. (2000 був високосним роком, оскільки, хоча він ділиться на 100, він також ділиться на 400.) Середня довжина григоріанського року становить 365.2425, що досить близько до Середнього тропічного року для сучасних цілей, але який викликає занепокоєння календарних реформаторів і буде викликати певну стурбованість наших віддалених нащадків.

    Аномалістичний рік - інтервал між послідовними проходами Землі через перигелій. Перигелій орбіти Землі повільно просувається в тому ж напрямку, що і рух Землі, тому аномалістичний рік трохи довше, ніж сидеричний рік, і дорівнює\(365^\text{d} .25964\).

    Малюнок\(\text{VI.9}\) ілюструє спосіб мислення про зв'язок між сидеричним і тропічним роками. Дивлячись вниз на екліптику з боку північного полюса екліптики. Ми бачимо, як Сонце рухається проти годинникової стрілки з кутовою швидкістю\(ω_\text{sid}\) і рухається за годинниковою стрілкою з\(ω_\Upsilon\) Кутова швидкість Сонця щодо\(\Upsilon\)

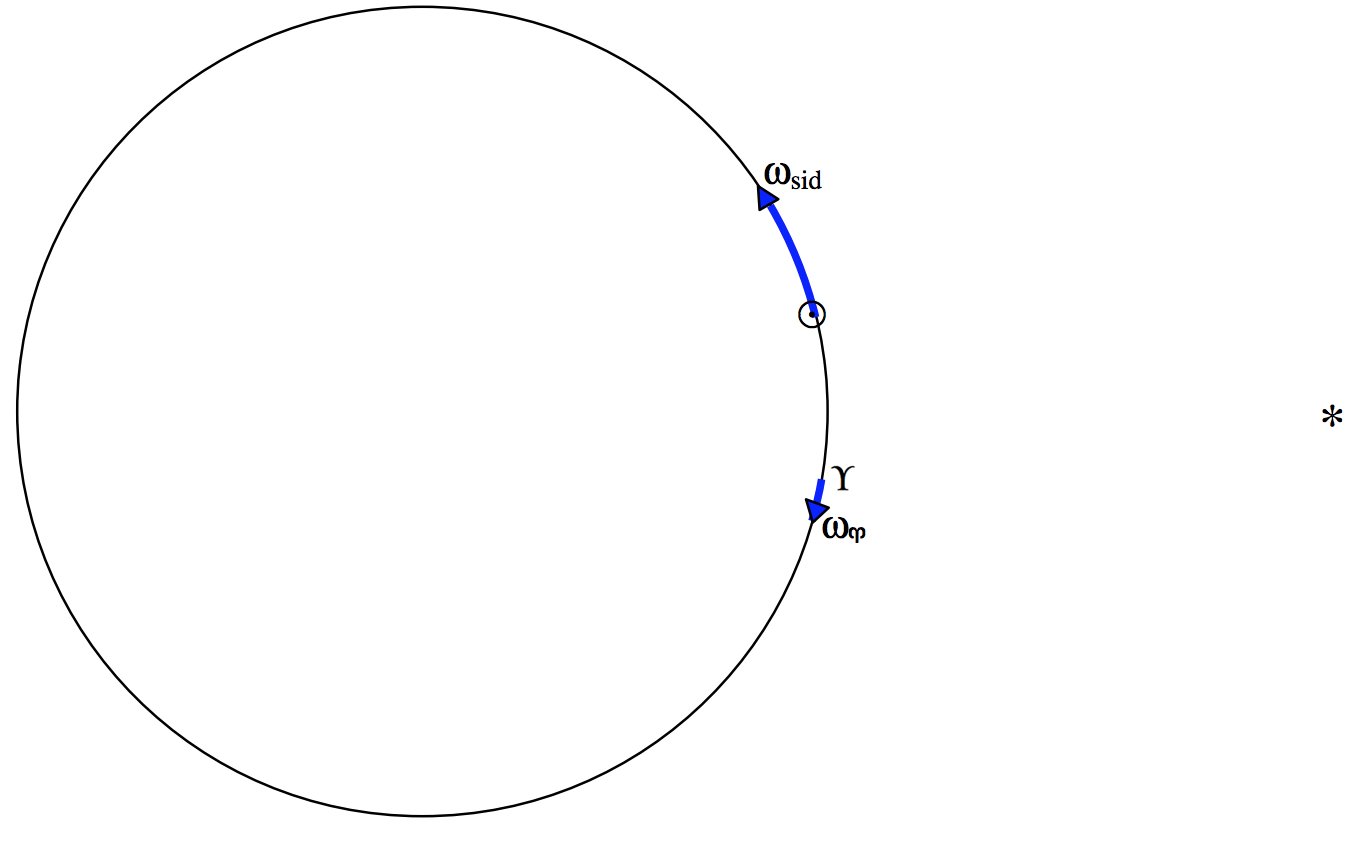
    Малюнок 6.9 copy.png
    \(\text{FIGURE VI.9}\)

    є\(ω_\text{trop} = ω_\text{sid} + ω_\Upsilon\). Але період\(P\) і кутова швидкість\(ω\) пов'язані між собою\(ω = 2π/P\).

    Тому:\[\frac{1}{P_\text{trop}} = \frac{1}{P_\text{sid}} + \frac{1}{P_\Upsilon}. \label{6.9.1} \tag{6.9.1}\]

    Таким чином\(P_\text{sid} = 365^\text{d} .25636\) і\(P_\Upsilon = 25800 \ \text{years} = 9.424 \times 10^6 \ \text{days}\). Звідси\(P_\text{trop} = 365^\text{d} .2422\). Використовуючи той самий аргумент, подивіться, чи можете ви обчислити, скільки часу потрібно перигелію орбіти Землі, щоб просунутися\(360^\circ\) - маючи на увазі, що перигелій просувається, а не регресує.

    Ще один момент, який варто відзначити, полягає в тому, що протягом сидеричного року Сонце пройшло верх через меридіан 365,25636 разів, тоді як фіксована зірка переходила 366,25636 разів. Виражається по-іншому, в той час як Земля обертається на своїй осі 365,25636 разів щодо Сонця, щодо зірок вона зробила один додатковий оборот під час свого обертання навколо Сонця. Таким чином

    \[\frac{\text{Length of sidereal day}}{\text{Length of solar day}} = \frac{365.25636}{366.25636}. \]

    Таким чином довжина сидеричного дня становить\(23^\text{h} \ 56^\text{m} \ 04^\text{s}\).