6.7: Прецесія

Перша точка Овна - точка, де екліптика перетинає екватор в точці, зайнятій Сонцем на березневому рівнодення. Це точка, з якої вимірюються праві піднесення. Ми досі ставилися до нього так, ніби він був зафіксований щодо зірок, хоча час від часу натякали, що це не зовсім так. Дійсно, ми говорили, що важливо, заявляючи про правильне сходження та схиляння зірки, вказати дату рівнодення, до якої вона посилається.

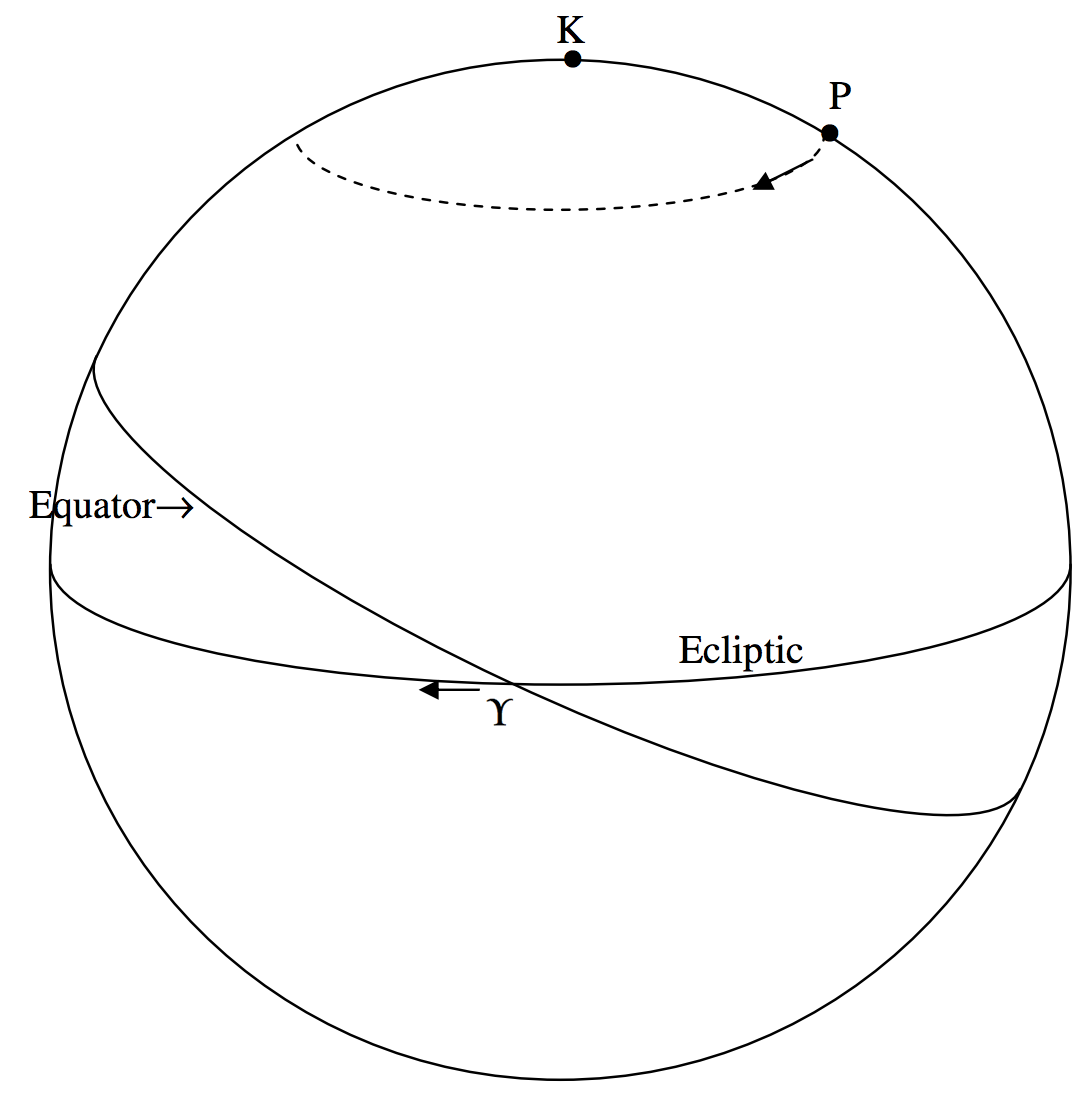
На малюнку$\text{VI.6}$ я намалював екліптику горизонтально, а небесний екватор нахилений під кутом$23^\circ .4$. Ви можете побачити північний полюс екліптики$\text{K}$, і північний небесний полюс$\text{P}$. Велике коло$\text{P} \Upsilon$ (не намальоване) - рівноцінний колір, а правильне сходження$\Upsilon$ є$0^h$. Правильне піднесення і схиляння$\text{K}$ є$18^h$$+66^\circ .6$, що є точкою між зірками$δ$ і$ζ$ Драконісом.

Однак ні північний небесний полюс,$\text{P}$ ні «Перша точка Овна» не$\Upsilon$ зафіксовані. Північний небесний полюс$\text{P}$ описує мале коло радіуса$23^\circ .4$ навколо$\text{K}$, а рівнодення регресує на захід уздовж екліптики в період 25 800 років. Цей рух, який називається прецесією рівнодення (або просто «прецесія» коротше), не зовсім рівномірний, але майже так і буде розглядатися як такий у цьому розділі. Повний цикл 25 800 років відповідає західній регресії$\Upsilon$ вздовж екліптики$50^{\prime \prime}.2$ на рік або$0^{\prime \prime}.137$ на добу. Складова цього руху вздовж небесного екватора становить$0^{\prime \prime}.137$$\cos 23^\circ .4 = 0^{\prime \prime} .126 = 0^{\text{s}} .008$ добу. Саме тому довжина середнього сидеричного дня (який визначається як інтервал між двома послідовними верхніми меридіанними транзитами першої точки Овна)$0^{\text{s}} .008$ коротша за період сидеричного обертання Землі.

Прецесія$\text{P}$ навколо$\text{K}$ означає, що вся система екваторіальних координат (правильне сходження і схилення) безперервно рухається, а правильні підйоми і схиляння всіх зірок безперервно змінюються. Незалежно від того, де$\text{P}$ знаходиться його подорож навколо$\text{K}$, однак, екваторіальні координати$\Upsilon$ і завжди$0^{\text{h}}$,$0^{\text{o}}$ і$18^\text{h}$,$+66^\text{o} .5$.$\text{K}$ Однак екваторіальні координати зірок завжди слід відносити до рівнодення та екватора заявленої епохи.

$\text{FIGURE VI.6}$

Протягом більшої частини двадцятого століття епоха, на яку йдеться багато каталогів та атласів, була$\text{B}1950.0$. Це початок Бессельського року 1950 року, в той момент (незадовго до півночі в ніч на 1949 31 груду/1950 січня 1), коли було правильне сходження Середнього Сонця$18^\text{h} 40^\text{m}$. Більшість каталогів, починаючи з 1984 року, віднесли права і відміни до середнього рівнодення і екватора$\text{J}2000.0$. Це початок юліанського року 2000, в той момент, коли середній час за Гринвічем (UT) вказав опівночі. Наприклад, у старих каталогах правильне сходження і схиляння Арктура було б дано як

$$α_{1950.0} = 14^\text{h} \quad 13^\text{m}.4 \quad δ_{1950.0} = +19^\circ 26^\prime,$$

тоді як в більш пізніх каталогах вони наведені як

$$α_{2000.0} = 14^\text{h} \quad 15^\text{m}.8 \quad δ_{2000.0} = +19^\circ 11^\prime .$$

Таким чином, видно, що для точної роботи різниця зовсім не незначна, і констатувати екваторіальні координати об'єкта, не вказуючи також епоху рівнодення та екватора, до яких посилаються координати, взагалі не корисно. Звичайно, встановлюючи кола телескопа для нічних спостережень, потрібно правильне сходження та схилення, що відноситься до рівнодення та екватора дати - тобто для дати, про яку йде мова. Тому практичному спостерігачеві важливо знати, як виправити прецесію.

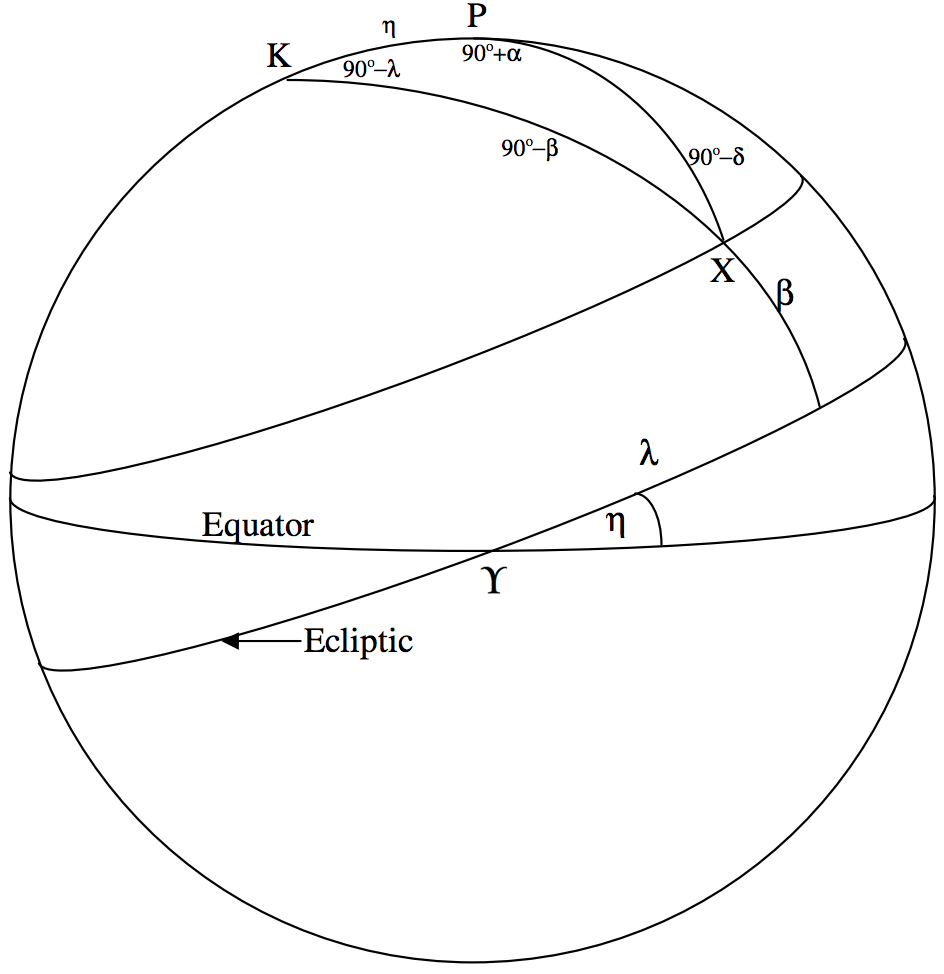
$\text{FIGURE VI.7}$

Застосуйте формулу косинуса (Рівняння 3.5.2) до трикутника$\text{PKX}$, щоб отримати

$$\sin δ = \cos η \sin β + \sin η \cos β \sin λ. \label{6.7.1} \tag{6.7.1}$$

$\Upsilon$Оскільки регресує вниз екліптика,$λ$ екліптична довгота зірки$\text{X}$ збільшується. Якщо вона збільшується$\ref{6.7.1}$ зі швидкістю на$\dot{λ}$$(= 50^{\prime \prime}.2$ рік), швидкість зміни його відмінювання можна отримати шляхом диференціації Рівняння по відношенню до часу, маючи на увазі, що$β$ і$η$ є постійними:

$$\cos δ \dot{δ} = \sin η \cos β \cos λ \dot{λ} . \label{6.7.2} \tag{6.7.2}$$

Але$(\cos β \cos λ)/\cosδ$ виходить з синусоїдальної формули (Рівняння 3.5.1):

$$\frac{\cos β}{\cos α} = \frac{\cos δ}{\cos λ} . \label{6.7.3} \tag{6.7.3}$$

Звідси отримаємо для швидкості зміни схиляння зірки внаслідок прецесії:

$$\dot{δ} = \dot{λ} \sin η \cos α . \label{6.7.4} \tag{6.7.4}$$

Щоб отримати швидкість зміни правого вознесіння, ми можемо записати Рівняння$\ref{6.7.3}$ як

$$\cos α = \cos β \sec δ \cos λ \label{6.7.5} \tag{6.7.5}$$

а потім диференціювати по відношенню до часу:

$$-\sin α \dot{α} = \cos β \sec δ (\tan δ \dot{δ} \cos λ - \sin λ \dot{λ}), \label{6.7.6} \tag{6.7.6}$$

який я збираюся написати як

$$-\sin α \dot{α} = \cos β \sec δ \cos λ ( \tan δ \dot{δ} - \tan λ \dot{λ}). \label{6.7.7} \tag{6.7.7}$$

Ми можемо отримати$\cos β \sec δ \cos λ$ від Рівняння$\ref{6.7.5}$, і, звичайно, ми маємо$δ$ з Рівняння$\ref{6.7.4}$, але нам все одно потрібно знайти вираз для$\tan λ$ екваторіальних координат. Ми можемо зробити це за формулою котангенса (Рівняння 3.5.4), в якій внутрішній кут є,$90^\circ + α$ а внутрішня сторона$η$:

$$-\cos η \sin α = \sin η \tan δ - \cos α \tan λ . \label{6.7.8} \tag{6.7.8}$$

При заміщенні рівнянь\ ref {6.7.4},\ ref {6.7.5} та\ ref {6.7.8} на рівняння\ ref {6.7.7} отримаємо, після дуже невеликої кількості алгебри, швидкість зміни правого сходження зірки внаслідок прецесії:

$$\dot{α} = \dot{λ} ( \cos η + \sin α \tan δ \sin η). \label{6.7.9} \tag{6.7.9}$$

З$\dot{λ} = 50^{\prime \prime}.2$ на рік і$η = 23^\circ .4$ рівняння\ ref {6.7.4} і\ ref {6.7.9} стають

$$\dot{δ} = 19^{\prime \prime} .9 \cos α \quad \text{per year} \label{6.7.10} \tag{6.7.10}$$

і $$\dot{α} = 46^{\prime \prime} .1 + 19^{\prime \prime} .9 \sin α \tan δ \quad \text{per year} \label{6.7.11} \tag{6.7.11}$$

або $$\dot{α} = 3^{s} .07 + 1^{\text{s}} .33 \sin α \tan δ \quad \text{per year}. \label{6.7.12} \tag{6.7.12}$$

Ці формули повинні бути адекватними для всіх, але дуже точних розрахунків.

Проблема: Використовуйте рівняння\ ref {6.7.10} і\ ref {6.7.12} для перевірки даних про Arcturus - і, будь ласка, дайте мені знати, якщо це не так!

За часів Гіппаркоса (який відкрив явище прецесії ще в другому столітті до н.е.) весняне рівнодення було в сузір'ї Овна — дійсно на його східній межі. Звідси її і назвали Першою точкою Овна. Протягом століть прецесія несла рівнодення на захід прямо через сузір'я Овен, і через це, разом з тим, як кордони сузір'я були офіційно закріплені в 1928 році, рівнодення зараз знаходиться поблизу західного кордону Риб і знаходиться всього в декількох градусах від Водолія. Його досі називають, однак, традиційною назвою Перша точка Овна. До речі, екліптика фактично проходить через сузір'я Змієносця, яке не є одним з традиційних дванадцяти «Знаків Зодіаку», і іноді говорять, що це результат прецесії протягом століть. Це не так. Прецесія не змінює площину екліптики, і екліптика продовжує проходити через одні й ті ж сузір'я незалежно від того, де рівнодення знаходиться вздовж неї. Включення Змієносця є лише результатом того, як кордони сузір'я були офіційно закріплені в 1928 році.

Фізична причина прецесії

Щоденний рух зірок навколо північного небесного полюса - це, звичайно, відображення обертання Землі на її осі; а річний рух Сонця по екліптиці, яка нахилена$23^\circ .4$ до небесного екватора, є відображенням річного орбітального руху Землі навколо Сонця, площини обертального екватора Землі, що нахиляється$23^\circ .4$ до площини її орбіти — тобто до екліптики. Хоча ця$23^\circ .4$ конусність приблизно постійна, напрямок осі обертання Землі не зафіксовано, але вона перегинається навколо нормалі до площини екліптики з періодом 25 800 років.

З точки зору класичної механіки Земля - сплющена симетрична вершина. Тобто він має вісь симетрії і два його основних моменти інерції рівні і менше моменту інерції навколо осі симетрії. Явища прецесії такого тіла добре вивчені і вивчаються на курсах класичної механіки. Однак необхідно чітко усвідомлювати різницю між прецесією без крутного моменту та прецесією, спричиненою крутним моментом.

Явище прецесії без крутного моменту - це прецесія, яка виникає, коли симетрична вершина обертається навколо осі, яка не збігається з її віссю симетрії, і вона вільно обертається без зовнішніх крутних моментів, що діють на неї. В таких умовах вектор кутового моменту фіксується за величиною і напрямком. Вісь симетрії переступає навколо фіксованого вектора кутового моменту, а миттєва вісь обертання переступає навколо осі симетрії. Обертання Землі дійсно демонструє такий тип поведінки, але це не прецесія, про яку ми говоримо у зв'язку з прецесією рівнодення. Миттєва вісь обертання Землі знаходиться всього в декількох метрах від її осі симетрії, а період прецесії без крутного моменту становить близько 432 днів. Це породжує явище, відоме як зміна широти, і це призводить до того, що широти місць розташування поверхні Землі змінюються квазіперіодично з амплітудою менше п'ятої секунди дуги. Прецесія рівнодення, про яку ми обговорювали в цьому розділі, - це щось зовсім інше.

Фігура Землі приблизно сплющена сфероїд. Якщо ми називаємо екваторіальний радіус$a$ і полярний радіус$c$, геометрична еліптичність$(a − c)/ a$ приблизно$1/297.0$. Якщо назвати відповідні основні моменти інерції$A$ і$C$, то динамічна еліптичність$(C − A)/ A$ приблизно$1/305.1$. Земний екватор нахилений до екліптики, і через екваторіальної опуклості обертається Земля схильна до крутним моментам як від Сонця, так і від Місяця (орбіта якої нахилена до екліптики приблизно на 5 градусів). Величина крутного моменту пропорційна діаметру Землі, що перевищує градієнт гравітаційного поля$2GM/r^3$, а напрямок вектора крутного моменту перпендикулярно вектору моменту.

Вправа$\PageIndex{1}$

Подивіться вгору маси Сонця і Місяця, і їх середні відстані від Землі. Покажіть, що$M/r^3$ для Місяця приблизно в два рази більше, ніж для Сонця. Таким чином, крутний момент на Землі, що чиниться Місяцем, приблизно вдвічі перевищує крутний момент, який надає Сонце.

Тепер, якщо симетрична вершина обертається навколо своєї осі симетрії з кутовим імпульсом$\textbf{L}$ і якщо вона піддається зовнішньому крутному моменту$\boldsymbol{\tau}$, його кутовий момент зміниться (не за величиною, а в напрямку), і$\textbf{L}$ буде переходити з кутовою швидкістю,$\boldsymbol{\Omega}$ заданою

$$\boldsymbol{\tau} = \boldsymbol{\Omega} \times \textbf{L}. \label{6.7.13} \tag{6.7.13}$$

Рівняння\ ref {6.7.13} не дає$\boldsymbol{\Omega}$ однозначного напрямку — що залежить від початкових умов. Малюнок$\text{VI.8}$ ілюструє ситуацію.

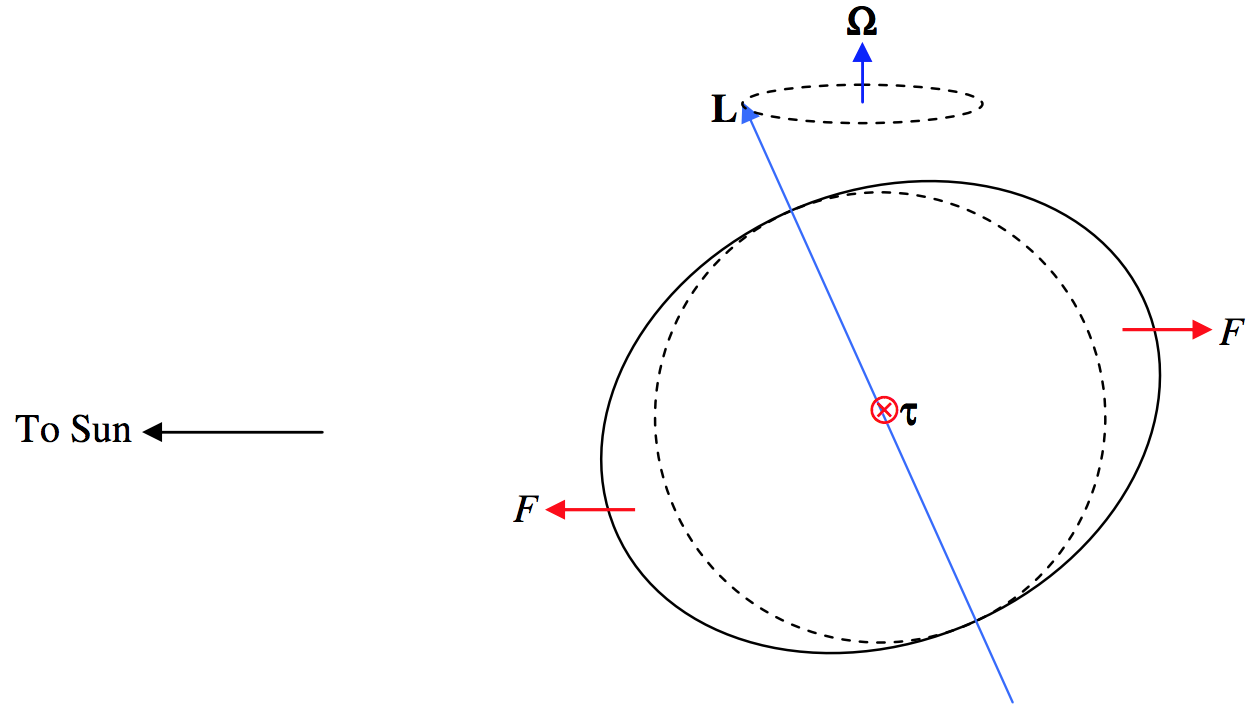
$\text{FIGURE VI.8}$

Екваторіальна опуклість набагато перебільшена. Фігура намальована в опорній рамці, яка обертається навколо Сонця з Землею, тому на Землі немає чистої гравітаційної сили (гравітаційному притяганню Сонця протидіє відцентрова сила). У цьому кадрі є невелика сила, що$F$ діє до Сонця на опуклість, звернену до сонця, і рівна сила, що діє від Сонця на протилежному боці. Це становить крутний момент величини$\tau = Fd \sin η$, де$η$ - конусність екліптики і$d$ діаметр Землі. Таким чином, якщо зрівняти величини обох сторін рівняння\ ref {6.7.13}, то отримаємо для кутової швидкості прецесії

$$\Omega = Fd / L , \label{6.7.14} \tag{6.7.14}$$

який є незалежним від$η$. Це, значить, є причиною прецесії рівнодення, хіба що, з метою фігури$\text{VI.8}$, я посилався тільки на Сонце. Ви самі підрахували, що вплив Місяця приблизно в два рази більше, ніж Сонця, а сукупний вплив Місяця і Сонця називається луні-сонячної прецесією. Існує невелика додаткова прецесія, що виникає внаслідок впливу інших планет Сонячної системи.

Дописувач

• Template:ContribTatum