32.3: Вектори

У цьому розділі ми розглянемо кілька понять, які ви, мабуть, знаєте зі своїх курсів фізики. Цей розділ не має наміру висвітлювати цю тему всебічно, а натомість торкнеться кількох понять, які ви будете використовувати на заняттях з фізичної хімії.

Вектор - це величина, яка має як величину, так і напрямок, і як така вони використовуються для визначення положення, швидкості та імпульсу частинки або для визначення сили. Вектори зазвичай позначаються жирним шрифтом (наприклад$\mathbf{u}$) або стрілкою над символом (наприклад$\vec{u}$). Тільда, розміщена над або під назвою вектора, також зазвичай використовується в скороченні ($\widetilde{u}$,$\underset{\sim}{u}$).

Якщо помножити число$a$ на вектор$\mathbf{v}$, ми отримаємо новий вектор, який паралельний оригіналу, але з довжиною, яка в$a$ рази перевищує довжину$\mathbf{v}$. Якщо$a$ негативні$a\mathbf{v}$ моменти в протилежну сторону ніж$\mathbf{v}$. Ми можемо висловити будь-який вектор через так звані одиничні вектори. Ці вектори, які позначаються$\hat{\mathbf{i}}$,$\hat{\mathbf{j}}$ і$\hat{\mathbf{k}}$, мають одиничну довжину і точку уздовж позитивної$x, y$ і$z$ осі декартової системи координат (рис.$\PageIndex{1}$). Символ$\hat{\mathbf{i}}$ читається «i-hat». Капелюхи використовуються для позначення того, що вектор має одиницю довжини.

Малюнок$\PageIndex{1}$: Ліворуч: Одиничні вектори. Праворуч: Вектор$\mathbf{u}$ може бути виражений через одиничні вектори як$\mathbf{u}=u_x\hat{\mathbf{i}}+u_y\hat{\mathbf{}j}+u_z\hat{\mathbf{k}}$ (CC BY-NC-SA; Marcia Levitus)

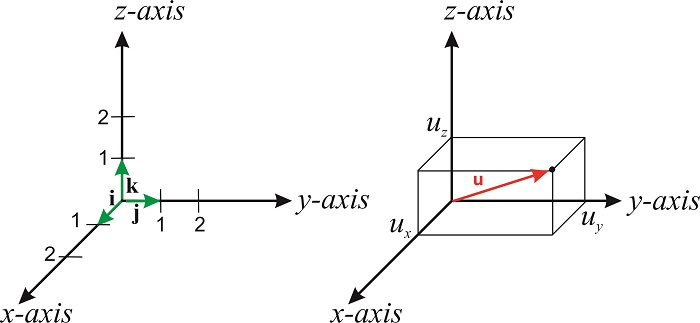
Довжина$\mathbf{u}$ - це його величина (або модуль), і зазвичай позначається$u$:

$$\label{eq:vectors1} u=|u|=(u_x^2+u_y^2+u_z^2)^{1/2}$$

Якщо у нас є два вектори$\mathbf{u}=u_x\hat{\mathbf{i}}+u_y \hat{\mathbf{j}}+u_z \hat{\mathbf{k}}$ і$\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}$, ми можемо додати їх для отримання

$$\mathbf{u}+\mathbf{v}=(u_x+v_x)\hat{\mathbf{i}}+(u_y+v_y)\hat{\mathbf{j}}+(u_z+v_z)\hat{\mathbf{k}} \nonumber$$

або відніміть їх, щоб отримати:

$$\mathbf{u}-\mathbf{v}=(u_x-v_x)\hat{\mathbf{i}}+(u_y-v_y)\hat{\mathbf{j}}+(u_z-v_z)\hat{\mathbf{k}} \nonumber$$

Коли справа доходить до множення, ми можемо виконати добуток двох векторів двома різними способами. Перший, який дає скаляр (число) в результаті, називається скалярним добутком або точковим добутком. Друге, що дає вектор в результаті, називається векторним (або перехресним) добутком. Обидва є важливими операціями з фізичної хімії.

Скалярний добуток

Скалярний добуток векторів$\mathbf{u}$ і$\mathbf{v}$, також відомий як крапковий добуток або внутрішній добуток, визначається як (зверніть увагу на крапку між символами, що представляють вектори)

$$\mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}|\cos \theta \nonumber$$

де$\theta$ - кут між векторами. Зверніть увагу, що точковий добуток дорівнює нулю, якщо два вектори перпендикулярні один одному, і дорівнює добутку їх абсолютних значень, якщо вони паралельні. Це легко довести, що

$$\mathbf{u}\cdot \mathbf{v}=u_xv_x+u_yv_y+u_zv_z \nonumber$$

Приклад$\PageIndex{1}$

Показати, що вектори

$$\begin{align*} \mathbf{u_1} &=\dfrac{1}{\sqrt{3}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_2} &=\dfrac{1}{\sqrt{6}}\hat{\mathbf{i}}-\dfrac{2}{\sqrt{6}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{6}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_3} &=-\dfrac{1}{\sqrt{2}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{2}}\hat{\mathbf{k}} \end{align*} \nonumber$$

мають одиницю довжини і взаємно перпендикулярні.

Рішення

Довжина векторів:

$$\begin{align*} |\mathbf{u_1}|&=\left[\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2\right]^{1/2}=\left[\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}\right]^{1/2}=1 \\[4pt] |\mathbf{u_2}| &=\left[\left(\dfrac{1}{\sqrt{6}}\right)^2+\left(-\dfrac{2}{\sqrt{6}}\right)^2+\left(\dfrac{1}{\sqrt{6}}\right)^2\right]^{1/2}=\left[\dfrac{1}{6}+\dfrac{4}{6}+\dfrac{1}{6}\right]^{1/2}=1 \\[4pt] |\mathbf{u_3}| &=\left[\left(-\dfrac{1}{\sqrt{2}}\right)^2+\left(\dfrac{1}{\sqrt{2}}\right)^2\right]^{1/2}=\left[\dfrac{1}{2}+\dfrac{1}{2}\right]^{1/2}=1 \end{align*} \nonumber$$

Щоб перевірити, чи два вектори перпендикулярні, виконуємо крапковий добуток:

$$\begin{align*} \mathbf{u_1}\cdot \mathbf{u_2}&=\left(\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{3}}\dfrac{2}{\sqrt{6}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}\right)=0 \\[4pt] \mathbf{u_1}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}\right)=0 \\[4pt] \mathbf{u_2}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}\right)=0 \end{align*} \nonumber$$

Тому ми тільки що довели, що три пари взаємно перпендикулярні, а три вектори мають одиничну довжину. Іншими словами, ці вектори є векторами$\hat{\mathbf{i}}$,$\hat{\mathbf{j}}$ і$\hat{\mathbf{k}}$ обертаються в просторі.

Якщо точковий добуток двох векторів (будь-якої розмірності) дорівнює нулю, ми говоримо, що два вектори ортогональні. Якщо вектори мають одиничну довжину, ми говоримо, що вони нормалізовані. Якщо два вектори є нормалізованими і вони ортогональні, ми говоримо, що вони ортонормальні. Набір векторів, показаний у попередньому прикладі, утворює ортонормальну множину. [vectors:orthonormal] Ці поняття також застосовуються до векторів, що містять складні записи, але як ми виконуємо точковий добуток у цьому випадку?

Загалом, квадрат модуля вектора дорівнює

$$|\mathbf{u}|^2=\mathbf{u}\cdot \mathbf{u}=u_x^2+u_y^2+u_z^2. \nonumber$$

Однак це не працює належним чином для складних векторів. Квадрат$i$ дорівнює -1, це означає, що ми ризикуємо мати непозитивні абсолютні значення. Для вирішення цього питання введемо більш загальну версію точкового добутку:

$$\mathbf{u}\cdot \mathbf{v}=u_x^*v_x+u_y^*v_y+u_z^*v_z, \nonumber$$

де «$*$» відноситься до складного сполученого. Тому для обчислення модуля вектора,$\mathbf{u}$ що має складні записи, використовуємо його складний сполучений:

$$|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u} \nonumber$$

Приклад$\PageIndex{2}$: Calculating the Modulus of a vector

Обчисліть модуль наступного вектора:

$$\mathbf{u}=\hat{\mathbf{i}}+i \hat{\mathbf{j}} \nonumber$$

Рішення

$$|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u}=(\hat{\mathbf{i}}-i \hat{\mathbf{j}})(\hat{\mathbf{i}}+i \hat{\mathbf{j}})=(1)(1)+(-i)(i)=2\rightarrow |\mathbf{u}|=\sqrt{2} \nonumber$$

Аналогічно, якщо вектори містять складні записи, ми можемо перевірити, чи є вони ортогональними чи ні, перевіряючи точковий добуток$\mathbf{u}^*\cdot \mathbf{v}$.

Приклад$\PageIndex{3}$: Confirming orthogonality

Визначте, чи є наступна пара векторів ортогональними (не плутайте ірраціональне число$i$ з одиничним вектором$\hat{\mathbf{i}}$!)

$$\mathbf{u}=\hat{\mathbf{i}}+(1-i)\hat{\mathbf{j}} \nonumber$$

і

$$\mathbf{v}=(1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}} \nonumber$$

Рішення

$$\mathbf{u}^*\cdot \mathbf{v}=(\hat{\mathbf{i}}+(1+i)\hat{\mathbf{j}})((1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}})=(1)(1+i)+(1+i)(1)=2+2i\neq 0 \nonumber$$

Тому вектори не ортогональні.

Векторний добуток

Векторний добуток двох векторів - вектор, який визначається як

$$\mathbf{u}\times \mathbf{v}=|\mathbf{u}| |\mathbf{v}| \mathbf{n} \sin\theta \nonumber$$

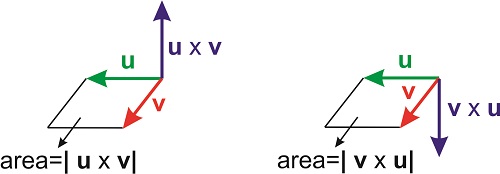
де$\theta$ знову кут між двома векторами, і$\mathbf{n}$ - одиничний вектор, перпендикулярний площині, утвореної$\mathbf{u}$ і$\mathbf{v}$. Напрямок вектора$\mathbf{n}$ задається правилом правої руки. Простягніть праву руку і наведіть вказівний палець у напрямку$\mathbf{u}$ (вектор на лівій стороні$\times$ символу) і вказівним пальцем у напрямку$\mathbf{v}$. Напрямок$\mathbf{n}$, який визначає напрямок$\mathbf{u}\times \mathbf{v}$, - це напрямок великого пальця. Якщо ви хочете повернути множення, і виконати$\mathbf{v}\times \mathbf{u}$, вам потрібно вказати вказівний палець у напрямку,$\mathbf{v}$ а вказівний палець у напрямку$\mathbf{u}$ (все ще використовуючи праву руку!). Отриманий вектор буде вказувати в протилежну сторону (рис.$\PageIndex{1}$).

Величина$\mathbf{u}\times \mathbf{v}$ - добуток величин окремих векторів разів$\sin \theta$. Ця величина має цікаву геометричну інтерпретацію: це площа паралелограма, утворена двома векторами (рис.$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Векторний добуток (CC BY-NC-SA; Марсія Левітус)

Перехресний добуток також може бути виражений як детермінант:

$$\mathbf{u}\times \mathbf{v}= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix} \nonumber$$

Приклад$\PageIndex{1}$:

Задано$\mathbf{u}=-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}$ і$\mathbf{v}=3 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}$, обчислити$\mathbf{w}=\mathbf{u}\times \mathbf{v}$ і перевірити, що результат перпендикулярний обох$\mathbf{u}$ і$\mathbf{v}$.

Рішення

$$\begin{align*} \mathbf{u}\times \mathbf{v} &= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix}=\begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ -2&1&1\\ 3&-1&1\\ \end{vmatrix} \\[4pt] &=\hat{\mathbf{i}}(1+1)-\hat{\mathbf{j}}(-2-3)+\hat{\mathbf{k}}(2-3) \\[4pt] &=\displaystyle{\color{Maroon}2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}-\hat{\mathbf{k}}} \end{align*} \nonumber$$

Щоб перевірити, що два вектори перпендикулярні, ми виконуємо крапковий добуток:

$$\mathbf{u} \cdot \mathbf{w}=(-2)(2)+(1)(5)+(1)(-1)=0 \nonumber$$

$$\mathbf{v} \cdot \mathbf{w}=(3)(2)+(-1)(5)+(1)(-1)=0 \nonumber$$

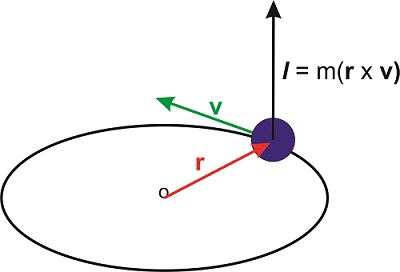
Важливе застосування перехресного виробу передбачає визначення моменту моменту. Якщо частка з масою$m$ рухає швидкість$\mathbf{v}$ (вектор), її (лінійний) імпульс дорівнює$\mathbf{p}=m\mathbf{v}$. $\mathbf{r}$Дозволяти положення частинки (інший вектор), тоді кутовий момент частки визначається як

$$\mathbf{l}=\mathbf{r}\times\mathbf{p} \nonumber$$

Таким чином, кутовий імпульс є вектором, перпендикулярним обом$\mathbf{r}$ і$\mathbf{p}$. Оскільки положення частинки потрібно визначити щодо певного походження, це походження потрібно вказати при визначенні кутового моменту.

Малюнок$\PageIndex{2}$: Кутовий момент частинки положення$\mathbf{r}$ від початку та імпульсу$\mathbf{p}=m\mathbf{v}$ (CC BY-NC-SA; Marcia Levitus)

Векторна нормалізація

Вектор будь-якої заданої довжини можна розділити за модулем, щоб створити одиничний вектор (тобто вектор одиничної довжини). Ми побачимо застосування одиничних (або нормалізованих) векторів у наступному розділі.

Наприклад, вектор

$$\mathbf{u}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+i\hat{\mathbf{k}} \nonumber$$

має величину:

$$|\mathbf{u}|^2=1^2+1^2+(-i)(i)=3\rightarrow |\mathbf{u}|=\sqrt{3} \nonumber$$

Тому для нормалізації цього вектора розділимо всі складові на його довжину:

$$\hat{\mathbf{u}}=\frac{1}{\sqrt{3}}\hat{\mathbf{i}}+\frac{1}{\sqrt{3}}\hat{\mathbf{j}}+\frac{i}{\sqrt{3}}\hat{\mathbf{k}} \nonumber$$

Зверніть увагу, що ми використовуємо «капелюх», щоб вказати, що вектор має одиницю довжини.

Потрібна допомога? Посилання нижче містять розв'язані приклади.

Операції з векторами: http://tinyurl.com/mw4qmz8

Зовнішні посилання:

• Точковий твір: http://patrickjmt.com/vectors-the-dot-product/
• Перехресний продукт: http://patrickjmt.com/the-cross-product/
• Точковий і хрестовий твір: http://www.youtube.com/watch?v=enr7JqvehJs