32.4: Сферичні координати

Цілі

• Зрозумійте поняття площі та об'ємних елементів у декартових, полярних та сферичних координатах.
• Вміти інтегрувати функції, виражені в полярних або сферичних координатах.
• Зрозумійте, як нормалізувати орбіталі, виражені в сферичних координатах, і виконувати обчислення за участю потрійних інтегралів.

Системи координат

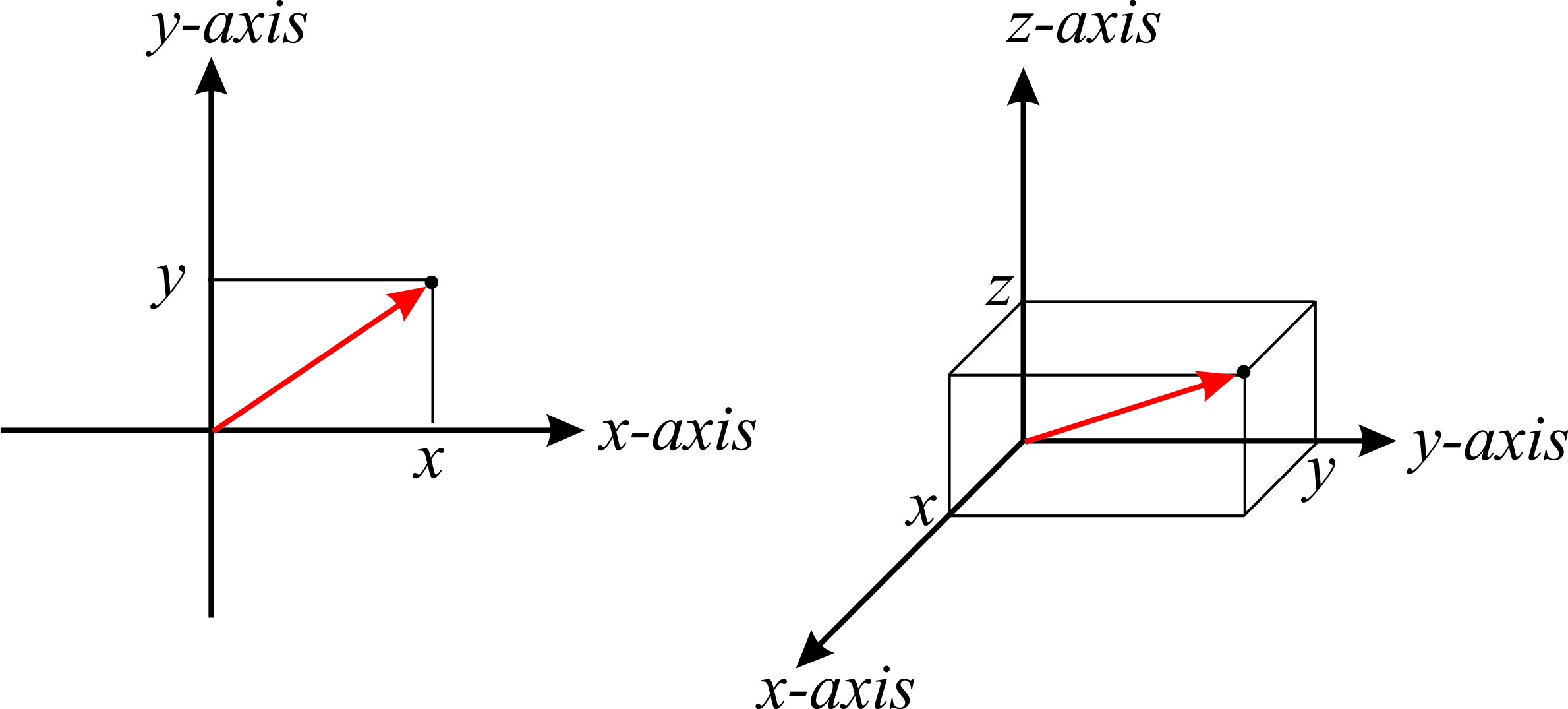
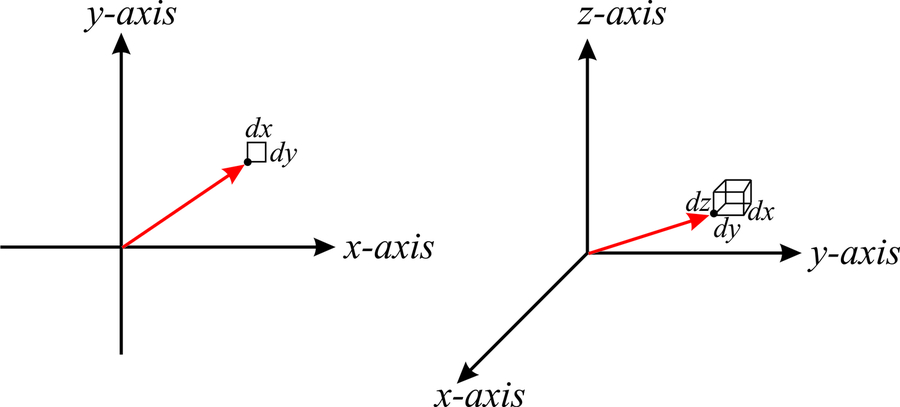
Найпростіша система координат складається з осей координат, орієнтованих перпендикулярно один одному. Ці координати відомі як декартові координати або прямокутні координати, і ви вже знайомі з їх двовимірним і тривимірним зображенням. У площині будь-яку точку$P$ можна представити двома підписаними числами, зазвичай записуються як$(x,y)$, де координата$x$ - відстань, перпендикулярна$x$ осі, а координата$y$ - відстань, перпендикулярне$y$ осі (рис.$\PageIndex{1}$, зліва). У просторі точка представлена трьома знаковими числами, зазвичай записуються як$(x,y,z)$ (рис.$\PageIndex{1}$, праворуч).

Часто позиції зображуються вектором$\vec{r}$, показаним червоним кольором на малюнку$\PageIndex{1}$. У трьох вимірах цей вектор може бути виражений через значення координат як$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$, де$\hat{i}=(1,0,0)$,$\hat{j}=(0,1,0)$ і$\hat{z}=(0,0,1)$ є так званими одиничними векторами.

Малюнок$\PageIndex{1}$: Декартові координати (CC BY-NC-SA; Марсія Левітус)

Ми вже знаємо, що часто симетрія проблеми робить її природною (і простішою!) використовувати інші системи координат. У двох вимірах полярна система координат визначає точку на площині двома числами: відстань$r$ до початку та кут,$\theta$ який вектор положення формує з$x$ віссю -. Зверніть увагу на різницю між$\vec{r}$, вектор$r$, і, відстань до початку (а отже, і модуль вектора). Вектори часто позначаються жирним шрифтом (наприклад, r) без стрілки зверху, тому будьте обережні, щоб не переплутати його з$r$, яка є скаляром.

Малюнок$\PageIndex{2}$: Плоскі полярні координати (CC BY-NC-SA; Марсія Левітус)

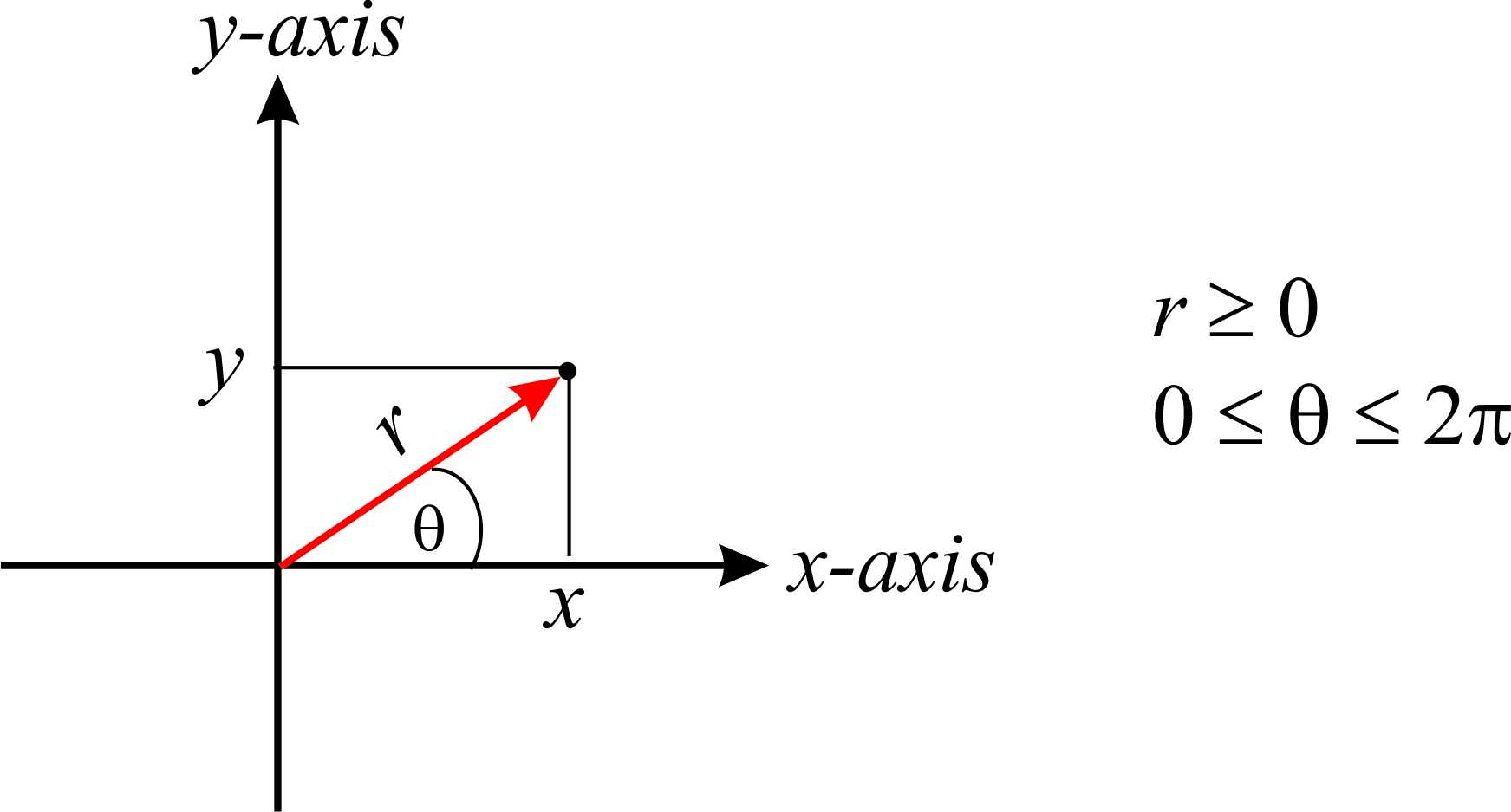
У той час як в декартових координатах$x$$y$ (і$z$ в тривимірних) можуть приймати значення від$-\infty$ до$\infty$, в полярних координатах$r$ є додатним значенням (узгоджується з відстанню), і$\theta$ може приймати значення в діапазоні$[0,2\pi]$.

Взаємозв'язок між декартовими і полярними координатами у двох вимірах можна узагальнити як:

$$\label{eq:coordinates_1} x=r\cos\theta$$

$$\label{eq:coordinates_2} y=r\sin\theta$$

$$\label{eq:coordinates_3} r^2=x^2+y^2$$

$$\label{eq:coordinates_4} \tan \theta=y/x$$

У трьох вимірах сферична система координат визначає точку в просторі трьома числами: відстань$r$ до початку, полярний кут,$\phi$ який вимірює кут між позитивною$x$ -віссю та лінією від початку до точки, що$P$ проектується на$xy$ -площину , і кут, який$\theta$ визначається як кут між$z$ -віссю і лінією від початку до точки$P$:

Малюнок$\PageIndex{3}$: Сферичні координати (CC BY-NC-SA; Марсія Левітус)

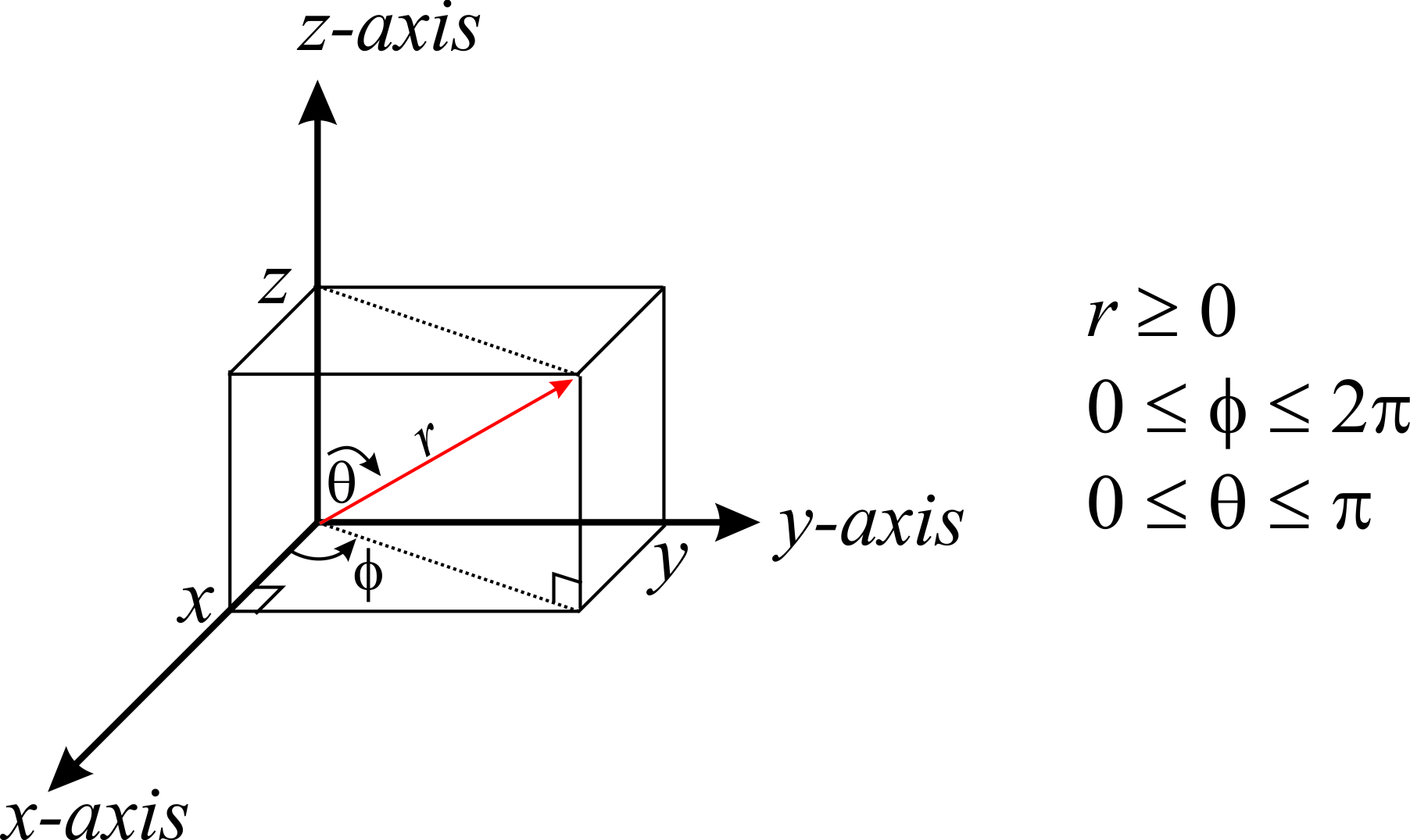
Перш ніж рухатися далі, важливо згадати, що залежно від поля, ви можете побачити грецьку букву$\theta$ (замість$\phi$), яка використовується для кута між позитивною$x$ віссю та лінією від початку до точки, що$P$ проектується на$xy$ площину -plane. Тобто$\theta$ і$\phi$ можуть з'явитися поміняні. Це може бути дуже заплутаним, тому доведеться бути обережним. При використанні сферичних координат важливо, щоб ви бачили, як ці два кути визначені, щоб ви могли визначити, який є який.

Сферичні координати корисні при аналізі систем, які симетричні щодо точки. Наприклад, сфера, яка має декартове рівняння,$x^2+y^2+z^2=R^2$ має дуже просте рівняння$r = R$ в сферичних координатах. Сферичні координати - це природні координати для фізичних ситуацій, коли існує сферична симетрія (наприклад, атоми). Взаємозв'язок між декартовими координатами та сферичними координатами можна узагальнити як:

$$\label{eq:coordinates_5} x=r\sin\theta\cos\phi$$

$$\label{eq:coordinates_6} y=r\sin\theta\sin\phi$$

$$\label{eq:coordinates_7} z=r\cos\theta$$

Ці відносини не важко вивести, якщо врахувати трикутники, показані на малюнку$\PageIndex{4}$:

Малюнок$\PageIndex{4}$: Сферичні координати (CC BY-NC-SA; Марсія Левітус)

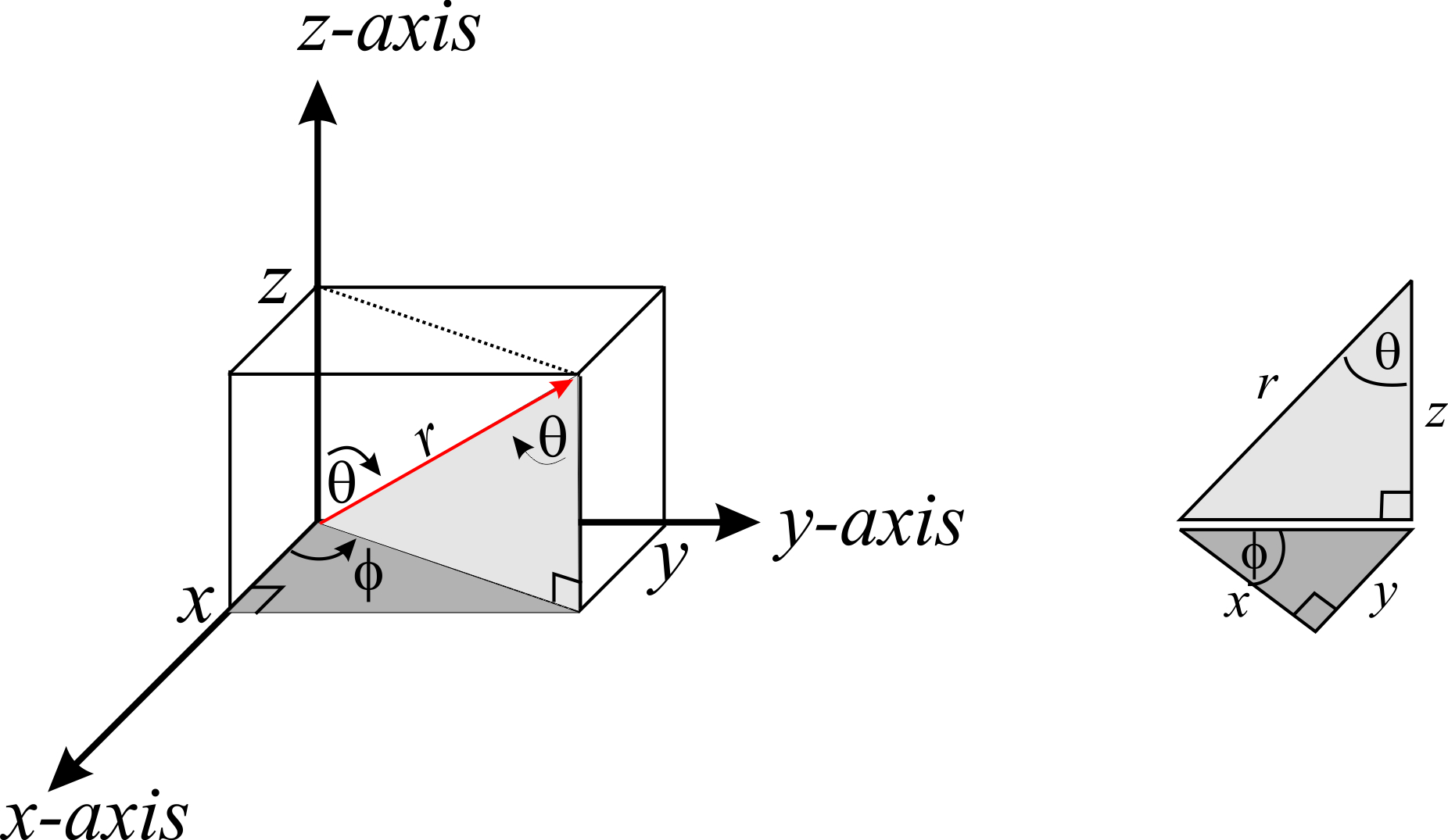
Елементи площі та об'єму

У будь-якій системі координат корисно визначити диференціальну площу та елемент диференціального об'єму. У декартових координатах елемент диференціальної площі просто$dA=dx\;dy$ (рис.$\PageIndex{1}$), а об'ємний елемент просто$dV=dx\;dy\;dz$.

Рисунок$\PageIndex{1}$: Елементи площі та об'єму в декартових координатах (CC BY-NC-SA; Marcia Levitus)

Ми вже виконували подвійні та потрійні інтеграли в декартових координатах і використовували елементи площі та об'єму, не звертаючи особливої уваги. Наприклад, у прикладі [c2v:c2vex1] нам було потрібно інтегрувати функцію${\left | \psi (x,y,z) \right |}^2$ по всьому простору, і, не замислюючись, ми використовували елемент volume$dx\;dy\;dz$ (див. сторінку). Ми також знали, що «весь простір» означає$-\infty\leq x\leq \infty$,$-\infty\leq y\leq \infty$ і$-\infty\leq z\leq \infty$, тому ми писали:

$$\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=1 \nonumber$$

Але що робити, якщо нам довелося інтегрувати функцію, яка виражається в сферичних координатах? Ми б просто замінити$dx\;dy\;dz$ на$dr\; d\theta\; d\phi$? Відповідь - ні, тому що елемент об'єму в сферичних координатах залежить також від фактичного положення точки. Це матиме більше сенсу через хвилину. Повертаючись до координат у двох вимірах, інтуїтивно зрозуміло, чому елемент площі в декартових координатах$dA=dx\;dy$ не залежить від значень$x$ і$y$. Це показано в лівій частині малюнка$\PageIndex{2}$. Однак в полярних координатах ми бачимо, що площі сірих ділянок, які як будуються$r$ збільшенням на$dr$, так і$\theta$ збільшенням на$d\theta$, залежать від фактичного значення$r$. Зверніть увагу, що область, виділена сірим кольором, збільшується, коли ми віддаляємося від початку.

Рисунок$\PageIndex{2}$: Диференціал площі в декартових і полярних координатах (CC BY-NC-SA; Marcia Levitus)

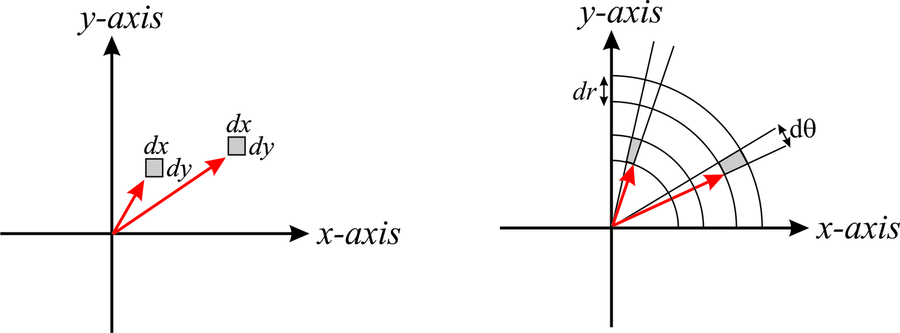
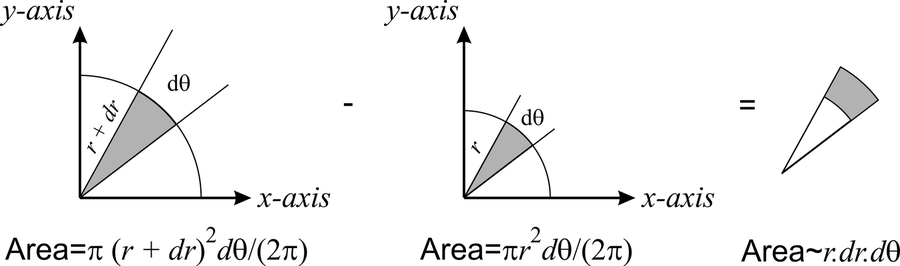
Площа, показана сірим кольором, може бути обчислена з геометричних аргументів як

$$dA=\left[\pi (r+dr)^2- \pi r^2\right]\dfrac{d\theta}{2\pi}.$$

Тому що$dr<<0$, можна знехтувати$(dr)^2$ терміном і$dA= r\; dr\;d\theta$ (див. Рис.$10.2.3$).

Малюнок$\PageIndex{3}$: Диференціал площі в полярних координатах (CC BY-NC-SA; Marcia Levitus)

Давайте подивимося, як це впливає на подвійний інтеграл на прикладі з квантової механіки. Хвильова функція наземного стану двовимірного гармонічного осцилятора становить:$\psi(x,y)=A e^{-a(x^2+y^2)}$. Ми знаємо, що величина$|\psi|^2$ являє собою щільність ймовірності, і як така, її потрібно нормалізувати:

$$\int\limits_{all\;space} |\psi|^2\;dA=1 \nonumber$$

Це твердження вірно незалежно від того, виражена функція в полярних або декартових координатах. Однак межі інтеграції та вираз, який використовується для$dA$, залежатимуть від системи координат, яка використовується в інтеграції.

У декартових координатах «весь простір» означає$-\infty<x<\infty$ і$-\infty<y<\infty$. Диференціал площі становить$dA=dxdy$:

$$\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty} A^2e^{-2a(x^2+y^2)}\;dxdy=1 \nonumber$$

У полярних координатах «весь простір» означає$0<r<\infty$ і$0<\theta<2\pi$. Диференціал площі є$dA=r\;drd\theta$. Функція$\psi(x,y)=A e^{-a(x^2+y^2)}$ може бути виражена в полярних координатах як:$\psi(r,\theta)=A e^{-ar^2}$

$$\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=1 \nonumber$$

Обидві версії подвійного інтеграла еквівалентні, і обидві можуть бути вирішені, щоб знайти значення константи нормалізації ($A$), що робить подвійний інтеграл рівним 1. У полярних координатах:

$$\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=A^2\int\limits_{0}^{\infty}e^{-2ar^2}r\;dr\int\limits_{0}^{2\pi}\;d\theta =A^2\times\dfrac{1}{4a}\times2\pi=1 \nonumber$$

Тому ¹,$A=\sqrt{2a/\pi}$. Таке ж значення, звичайно, отримується шляхом інтеграції в декартові координати.

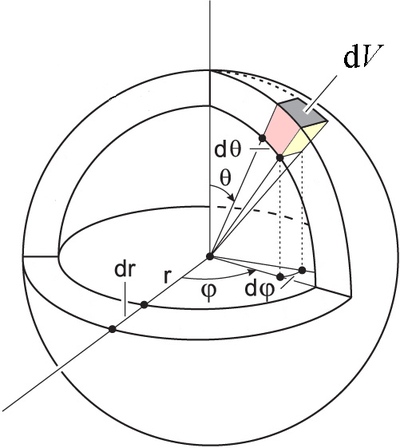
Настав час звернути нашу увагу на потрійні інтеграли в сферичних координатах. У декартових координатах диференціальний об'ємний елемент просто$dV= dx\,dy\,dz$, незалежно від значень$x, y$ і$z$. Використовуючи ті самі аргументи, які ми використовували для полярних координат в площині, ми побачимо, що диференціала об'єму в сферичних координатах немає$dV=dr\,d\theta\,d\phi$. Геометричне виведення об'єму трохи складніше, але з малюнка$\PageIndex{4}$ ви повинні бути в змозі побачити, що$dV$ залежить від$r$ і$\theta$, але не від$\phi$. Обсяг затіненої області дорівнює

$$\label{eq:dv} dV=r^2\sin\theta\,d\theta\,d\phi\,dr$$

Рисунок$\PageIndex{4}$: Диференціал об'єму в сферичних координатах (CC BY-NC-SA; Marcia Levitus)

Ми наведемо приклад використання потрійних інтегралів у сферичних координатах з деякими задачами квантової механіки. Ми вже ввели рівняння Шредінгера і навіть розв'язали його для простої системи в розділі 5.4. Ми також згадували, що сферичні координати є очевидним вибором при написанні цього та інших рівнянь для таких систем, як атоми, які симетричні навколо точки.

Як ми бачили у випадку з частинкою в коробці (Розділ 5.4), рішення рівняння Шредінгера має довільну мультиплікативну константу. Через імовірнісну інтерпретацію хвильових функцій ми визначаємо цю константу шляхом нормалізації. Така ж ситуація виникає в трьох вимірах, коли ми вирішуємо рівняння Шредінгера для отримання виразів, які описують можливі стани електрона в атомі водню (тобто орбіталі атома). Рівняння Шредінгера - це рівняння з частинними похідними в трьох вимірах, і розв'язками будуть хвильові функції, які є функціями$r, \theta$ і$\phi$. Найнижчий енергетичний стан, який в хімії ми називаємо орбітальною 1s, виявляється:

$$\psi_{1s}=Ae^{-r/a_0} \nonumber$$

Ця конкретна орбіталь залежить$r$ тільки від того, що не повинно дивувати хіміка, враховуючи, що електронна щільність у всіх$s$ -орбіталів сферично симетрична. Ми побачимо, що$p$ і$d$ орбіталі залежать і від кутів. Незалежно від орбітальної, і системи координат, умова нормалізації говорить, що:

$$\int\limits_{all\;space} |\psi|^2\;dV=1 \nonumber$$

Для хвильової функції, вираженої в декартових координатах,

$$\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\psi^*(x,y,z)\psi(x,y,z)\,dxdydz \nonumber$$

де ми використовували те, що$|\psi|^2=\psi^* \psi$.

У сферичних координатах «весь простір» означає$0\leq r\leq \infty$,$0\leq \phi\leq 2\pi$ і$0\leq \theta\leq \pi$. Диференціал$dV$ є$dV=r^2\sin\theta\,d\theta\,d\phi\,dr$, так

$$\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber$$

Давайте подивимося, як ми можемо нормалізувати орбіталі за допомогою потрійних інтегралів у сферичних координатах.

Приклад$\PageIndex{1}$

При вирішенні рівняння Шредінгера для атома водню отримаємо$\psi_{1s}=Ae^{-r/a_0}$, де$A$ знаходиться довільна константа, яку потрібно визначити шляхом нормалізації. Знайти$A$.

Рішення

У сферичних координатах,

$$\int\limits_{all\; space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber$$

тому що ця орбітальна є реальною функцією,$\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)=\psi^2(r,\theta,\phi)$. В даному випадку,$\psi^2(r,\theta,\phi)=A^2e^{-2r/a_0}$.

Тому,

$$\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi) \, r^2 \sin\theta \, dr d\theta d\phi=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber$$

$$\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr \nonumber$$

Результатом є добуток трьох інтегралів в одну змінну:

$$\int\limits_{0}^{2\pi}d\phi=2\pi \nonumber$$

$$\int\limits_{0}^{\pi}\sin\theta \;d\theta=-\cos\theta|_{0}^{\pi}=2 \nonumber$$

$$\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=? \nonumber$$

З листа формул:

$$\int_{0}^{\infty}x^ne^{-ax}dx=\dfrac{n!}{a^{n+1}}, \nonumber$$

де$a>0$ і$n$ - натуральне число.

У цьому випадку$n=2$ і$a=2/a_0$, так:

$$\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=\dfrac{2!}{(2/a_0)^3}=\dfrac{2}{8/a_0^3}=\dfrac{a_0^3}{4} \nonumber$$

Збираємо три частини разом:

$$A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=A^2\times2\pi\times2\times \dfrac{a_0^3}{4}=1 \nonumber$$

$$A^2\times \pi \times a_0^3=1\rightarrow A=\dfrac{1}{\sqrt{\pi a_0^3}} \nonumber$$

Отже, нормалізована орбітальна 1s є:

$$\displaystyle{\color{Maroon}\dfrac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}} \nonumber$$