7.2: Ентропна еластичність

Ідеальна модель ланцюга

Більшість полімерних ланцюгів мають поворотні зв'язки, а також кути зв'язку вздовж полімерної магістралі, які відрізняються від 180$^\circ$. Це призводить до гнучкості ланцюга. Навіть якщо обертання не вільні, а породжують лише$n_\mathrm{rot}$ ротамерні стани на обертовий зв'язок, кількість можливих конформацій ланцюга стає величезною. Для$N_{rot}$ обертових зв'язків кількість різних конформацій становить$n_\mathrm{rot}^{N_\mathrm{rot}}$. Найпростішою корисною моделлю для такої гнучкої ланцюга є вільно з'єднана модель ланцюга. Тут ми припускаємо вектори зв'язку$l = |\vec{r}_i|$, які мають однакову довжину, де$\vec{r}_i$ вектор зв'язку$i^\mathrm{th}$ зв'язку. Якщо ми далі припустимо кут$\theta_{ij}$ між послідовними векторами зв'язку, ми можемо записати скалярний добуток послідовних векторів зв'язків як

$$\vec{r}_i \cdot \vec{r}_j = l^2 \cos \theta_{ij} \ . \label{eq:fjc_cons}$$

Цей скалярний твір представляє інтерес, оскільки ми можемо використовувати його для обчислення середньоквадратичної$\langle R^2 \rangle$ наскрізної відстані ансамблю ланцюгів, що є найпростішим параметром, що характеризує просторову розмірність ланцюга. З наскрізним вектором відстані ланцюга з$n$ зв'язками,

$$\vec{R}_n = \sum_{i=1}^n \vec{r}_i \ ,$$

у нас є

$$\begin{align} \langle R^2 \rangle & = \langle \vec{R}_n^2 \rangle \\ & = \langle \vec{R}_n \cdot \vec{R}_n \rangle \\ & = \left\langle \left( \sum_{i=1}^n \vec{r}_i \right) \cdot \left( \sum_{j=1}^n \vec{r}_j \right) \right\rangle \\ & = \sum_{i=1}^n \sum_{j=1}^n \langle \vec{r}_i \cdot \vec{r}_j \rangle \ .\end{align}$$

Використовуючи рівняння\ ref {eq:fjc_cons}) ми знаходимо

$$\langle R^2 \rangle = l^2 \sum_{i=1}^n \sum_{j=1}^n \langle \cos \theta_{ij} \rangle \ . \label{eq:fjc_double_sum}$$

У моделі вільно з'єднаних ланцюгів ми далі припускаємо, що немає кореляцій між напрямками різних векторів зв'язку,$\langle \cos \theta_{ij} \rangle = 0$ для$i \neq j$. Тоді подвійна сума в Equation\ ref {eq:fjc_double_sum}) має лише$n$ ненульові члени для$i=j$ with$\cos \theta_{ij} = 1$. Отже,

$$\langle R^2 \rangle = n l^2 \ . \label{eq:eer_fjc}$$

Це знову здається грубою моделлю, але тепер ми врятуємо її, переглянувши$l$. В ідеальному полімерному ланцюжку ми можемо принаймні припустити, що немає взаємодії між мономерами, які розділені багатьма іншими мономерами,

$$\lim\limits_{|i-j| \rightarrow \infty} \langle \cos \theta_{ij} \rangle = 0 \ .$$

Крім того, для заданого вектора зв'язку сума$\vec{r}_i$ по всіх кореляціях з іншими векторами зв'язків збігається до деякого скінченного числа, яке залежить від$i$,

$$\sum_{j=1}^n \langle \cos \theta_{ij} \rangle = C'(i) \ .$$

Тому при включенні кореляцій рівняння\ ref {eq:fjc_double_sum}) все ще можна спростити до

$$\langle R^2 \rangle = l^2 \sum_{i=1}^n C'(i) = C_n n l^2 \ ,$$

де характеристичне співвідношення Флорі$C_n$ - середнє значення$C'(i)$ по всіх магістральних зв'язках ланцюга.

Загалом,$C_n$ залежить від$n$, але для дуже довгих ланцюгів він сходиться до значення$C_\infty$. Для досить довгих ланцюгів ми можемо таким чином наблизити

$$\langle R^2 \rangle \approx n C_\infty l^2 \ ,$$

яка має таку ж залежність від$n$ і$l$ як сирої моделі вільно з'єднаного ланцюга, Equation\ ref {eq:eer_fjc}). Отже, ми можемо визначити еквівалентну вільно з'єднану ланцюг з$N$ відрізками Куна довжиною$b$. Від

$$\langle R^2 \rangle = N b^2 \approx n C_\infty l^2 \label{eq:Kuhn_R2}$$

і довжину максимально розтягнутої еквівалентної ланцюга, довжину контуру$R_\mathrm{max}$,

$$R_\mathrm{max} = N b \ ,$$

отримуємо

$$N = \frac{R_\mathrm{max}^2}{C_\infty n l^2}$$

і довжина Куна

$$b = \frac{\langle R^2 \rangle}{R_\mathrm{max}} = \frac{C_\infty n l^2}{R_\mathrm{max}} \ .$$

Типові значення$C_\infty$ для синтетичних полімерів коливаються від 4,6 для 1,4-полі (ізопрен) до 9,5 для атактичного полі (стирол) з відповідними довжинами Куна 8,2 Å до 18 Å відповідно.

На цьому етапі ми знайшли середньоквадратичну наскрізну відстань як параметр рівноважного макростану. Якщо ми розтягуємо ланцюг до більшої відстані від кінця до кінця, вона більше не знаходиться в рівновазі і повинна мати більшу вільну енергію. Частина цього збільшення вільної енергії повинна відбуватися від зменшення ентропії, що розтягнення індукує зменшенням кількості доступних ланцюгових конформацій. Виявляється, цей ентропний внесок є основною частиною збільшення вільної енергії, як правило, 90%. Тенденція полімерних ланцюгів скорочуватися після їх розтягування, таким чином, є головним чином ентропним ефектом. Щоб кількісно оцінити його, нам потрібен розподіл ймовірностей для наскрізних векторів, і з цією метою ми вводимо поняття, яке широко використовується в природничих науках.

Випадкова прогулянка

Модель вільно з'єднаного ланцюга явно передбачає, що напрямок наступного сегмента Куна не співвідноситься з напрямками всіх попередніх сегментів Куна. Де буде розташовуватися кінець ланцюга після наступного кроку, який подовжує ланцюг на один відрізок, залежить тільки від місця розташування поточного кінця ланцюга. Таким чином, вільно з'єднаний ланцюг має аспекти ланцюга Маркова. Кожен крок подовження - це випадкова подія і траєкторія ланцюга в просторі випадкової ходьби.

Багато процесів можуть бути дискретизовані на окремі етапи. Те, що відбувається на наступному кроці, може залежати лише від поточного стану, а також від того, що сталося на попередніх кроках. Якщо це залежить тільки від поточного стану, процес є незапам'ятовуваним і підходить під визначення марковського ланцюжка. Ланцюжок Маркова, де події є аналогічними кроками в деякому просторі параметрів, можна змоделювати як випадкову прогулянку. Випадкова прогулянка - це математично формалізована послідовність випадкових кроків. Випадкова прогулянка по решітці, де кожен крок може вести лише від точки решітки до безпосередньо сусідньої точки решітки, є особливо простою моделлю. [концепція: випадковий_прогулянка]

Ми можемо використовувати поняття випадкової ходьби в поєднанні з поняттями статистичної термодинаміки для вирішення проблеми розтягування і стиснення полімерного ланцюга. Задача вирішується, якщо знати залежність вільної енергії Гельмгольца від довжини наскрізного вектора. Це, в свою чергу, вимагає, щоб ми знали ентропію і, таким чином, розподіл ймовірностей довжини наскрізного вектора. Цей розподіл ймовірностей задається кількістю можливих випадкових прогулянок (траєкторій), які ведуть до певної наскрізної відстані$\sqrt{\vec{R}^2}$.

Для простоти ми починаємо з більш простого прикладу в одному вимірі, який згодом ми можемо розширити до трьох вимірів. Розглянемо стандартний приклад в цій галузі, п'яниця, щойно покинула паб. Припускаємо, що, починаючи з дверей пабу, він робить випадкові кроки вперед і назад по дорозі. Яка ймовірність того$P(N,x)$, що після$N$ кроків він знаходиться на відстані$x$ сходинок вгору по дорозі від дверей пабу? Задача еквівалентна знаходженню$W(N,x)$ кількості траєкторій довжини$N$, що закінчуються$x$ кроками від дверей пабу, та поділу її на загальну кількість траєкторій.

Будь-яка така траєкторія складається з$N_+$ кроків вгору по дорозі і$N_-$ сходинок вниз по дорозі, при цьому кінцева позиція є$x = N_+ - N_-$. Кількість таких траєкторій, знову ж таки, задається біноміальним розподілом (див. Розділ [binomial_distribution])

$$W(N,x) = \frac{\left( N_+ + N_-\right)!}{N_+! N_-!} = \frac{N!}{\left[ \left(N+x\right)/2\right] ! \left[ \left(N-x\right)/2\right] !} \ ,$$

тоді як загальна кількість траєкторій є$2^N$, оскільки п'яниця має дві можливості на кожному кроці. Отже,

$$P(N,x) = \frac{1}{2^N} \cdot \frac{N!}{\left[ \left(N+x\right)/2\right] ! \left[ \left(N-x\right)/2\right] !} \ ,$$

приводячи до

$$\ln P(N,x) = -N \ln 2 + \ln(N!) - \ln \left(\frac{N+x}{2}\right)! - \ln \left(\frac{N-x}{2}\right)! \ .$$

Останні два терміни з правого боку можна переписати як

$$\begin{align} \ln \left(\frac{N + x}{2}\right)! = \ln \left(\frac{N}{2}\right)! + \sum_{s=1}^{x/2} \ln \left( \frac{N}{2} + s \right) \ \textrm{and} \\ \ln \left(\frac{N - x}{2}\right)! = \ln \left(\frac{N}{2}\right)! - \sum_{s=1}^{x/2} \ln \left( \frac{N}{2} + 1 - s \right) \ ,\end{align}$$

що призводить до

$$\ln P(N,x) = -N \ln 2 + \ln(N!) - 2\ln \left(\frac{N}{2}\right)! - \sum_{s=1}^{x/2} \ln \left( \frac{N/2 + s}{N/2 + 1 - s} \right) \ . \label{eq:P_N_X_0}$$

Тепер ми припускаємо довгу траєкторію. У діапазоні де$x \ll N$, який реалізується в переважній частці всіх траєкторій, логарифми чисельника і знаменника в останньому семестрі праворуч Equation\ ref {eq:p_n_x_0}) можуть бути наближені розширенням рядів,$\ln(1+y) \approx y$ для$|y| \ll 1$, що дає

$$\begin{align} \ln \left( \frac{N/2 + s}{N/2 + 1 -s} \right) & = \ln \left( \frac{1 + 2s/N}{1 -2s/N + 2/N} \right) \\ & = \ln \left( 1 + \frac{2s}{N} \right) - \ln\left( 1 - \frac{2s}{N} + 2/N \right) \\ & \approx \frac{4s}{N} - \frac{2}{N} \ . \label{eq:Gauss_approx_0}\end{align}$$

Отже,

$$\begin{align} \sum_{s=1}^{x/2} \ln \left( \frac{N/2 + s}{N/2 + 1 - s} \right) & = \sum_{s=1}^{x/2} \left( \frac{4s}{N} - \frac{2}{N} \right) \\ & = \frac{4}{N} \sum_{s=1}^{x/2} s - \frac{2}{N} \sum_{s=1}^{x/2} 1 \\ & = \frac{4}{N} \cdot \frac{(x/2)(x/2+1)}{2} - \frac{x}{N} \\ & = \frac{x^2}{2N} \ . \label{eq:Gauss_approx}\end{align}$$

Вставка рівняння\ ref {EQ:Gauss_apcol} в рівняння\ ref {EQ:P_n_x_0}) забезпечує,

$$P(N,x) \approx \frac{1}{2^N} \cdot \frac{N!}{(N/2)!(N/2)!} \cdot \exp\left( - \frac{x^2}{2N} \right) \ ,$$

де ми визнаємо, в останньому факторі праворуч, наближення біноміального розподілу розподілом Гаусса, який ми обговорювали в розділі [binomial_distribution]. Використовуючи вдосконалену формулу Стірлінга, Equation\ ref {EQ:Stirling_better}), для вираження факторіалів ми маємо

$$\frac{1}{2^N} \cdot \frac{N!}{(N/2)!(N/2)!} = \frac{1}{2^N} \frac{\sqrt{2 \pi N} N^N \exp(-N)}{\left(\sqrt{\pi N} (N/2)^{N/2} \exp(-N/2)\right)^2} = \sqrt{\frac{2}{\pi N}} \ ,$$

що призводить до надзвичайно простого результату:

$$P(N,x) = \sqrt{\frac{2}{\pi N}} \exp\left( - \frac{x^2}{2N} \right) \ .$$

П'яниця, якщо приділяється достатньо часу і не засинає, прекрасно імітує гауссовое розподіл.

Ми можемо ще більше спростити цей результат, запитуючи про середнє$\langle x^2 \rangle$ квадратне зміщення, яке дається

$$\langle x^2 \rangle = \int_{-\infty}^{\infty} x^2 P(N,x) \mathrm{d}x = \sqrt{\frac{2}{\pi N}} \int_{-\infty}^{\infty} x^2 \exp\left( - \frac{x^2}{2N} \right) \mathrm{d}x = N \ .$$

Перш ніж ми продовжимо, нам потрібно виправити проблему, яка виникає, коли ми інтерпретуємо дискретні ймовірності, обчислені в цей момент, як безперервний розподіл щільності ймовірностей$x$. У дискретному випадку$W(N,x)$ може бути ненульовим тільки для парних або непарних$x$, в залежності від того,$N$ парний або непарний. Таким чином, щоб прийти до правильного розподілу ймовірностей, нам потрібно розділити на 2. Отже, ми можемо виразити розподіл щільності ймовірності для одновимірної випадкової ходьби як

$$\rho_\mathrm{1d}(x) = \frac{1}{\sqrt{2\pi \langle x^2 \rangle}} \exp\left( - \frac{x^2}{2\langle x^2 \rangle} \right) \ .$$

Цей результат більше не залежить від розміру кроку, навіть неявно, тому що ми прибрали залежність від номера кроку$N$. Тому його можна узагальнити до трьох вимірів. Оскільки випадкові прогулянки по трьох попарно ортогональних напрямках в декартовому просторі незалежні один від одного, ми маємо

$$\rho_\mathrm{3d}(x,y,z) \mathrm{d}x \mathrm{d} y \mathrm{dz} = \rho_\mathrm{1d}(x) \mathrm{d}x \cdot \rho_\mathrm{1d}(y) \mathrm{d}y \cdot \rho_\mathrm{1d}(z) \mathrm{d}z \ .$$

На цьому етапі ми пов'язуємо результат з конформаційним ансамблем ідеального полімерного ланцюга, використовуючи модель Куна, розглянуту в розділі [subsect:ideal_chain]. Поставлено питання про розподіл середньоквадратичних наскрізних відстаней$\left\langle \vec{R}^2 \right\rangle$ з декартовими складовими наскрізного вектора$\vec{R}$ буття$x = R_x$$y = R_y$, і$z = R_z$. Відповідно до рівняння\ ref {EQ:KUHN_R2}), ми маємо

$$\begin{align} \left\langle \vec{R}^2 \right\rangle & = \left\langle R_x^2 \right\rangle + \left\langle R_y^2 \right\rangle + \left\langle R_z^2 \right\rangle \label{eq:R2_xyz} \\ & = N b^2 \ .\end{align}$$

З міркувань симетрії ми маємо,

$$\left\langle R_x^2 \right\rangle = \left\langle R_y^2 \right\rangle = \left\langle R_z^2 \right\rangle = \frac{N b^2}{3} \ ,$$

приводячи до

$$\rho_\mathrm{1d}(N,x) = \sqrt{\frac{3}{2 \pi N b^2}} \exp \left( -\frac{3R_x^2}{2N b^2} \right)$$

і аналогічні вирази для$\rho_\mathrm{1d}(y)$ і$\rho_\mathrm{1d}(z)$. Ми знову ввели параметр$N$, який тепер є кількістю сегментів Куна. Однак, обговорюючи безперервний розподіл густини ймовірностей, ми усунули залежність від ґратчастої моделі. Це необхідно, так як ступені за розмірами$x$$y$, і$z$ відрізняються для кожного сегмента Куна. Використовуючи рівняння\ ref {EQ:R2_xYZ}), знаходимо

$$\rho_\mathrm{3d}(N,\vec{R}) = \left( \frac{3}{2 \pi N b^2} \right)^{3/2} \exp \left(-\frac{3 \vec{R}^2}{2 N b^2} \right) \ . \label{eq:rho3d_chain}$$

Щільність ймовірності досягає максимуму при нульовому наскрізному векторі.

Малюнок$\PageIndex{1}$: Наскрізний розподіл відстані ідеального ланцюга. (A) Розподіл щільності$\rho_\mathrm{3d}(N,R)$ ймовірностей нормованих відстаней від кінця до кінця$R/(b\sqrt{N})$. (B) Сукупний розподіл ймовірностей, що вказує на ймовірність знайти ланцюг з наскрізною відстанню менше$R/(b\sqrt{B})$. Трохи більше 60% всіх ланцюгів (червона пунктирна горизонтальна лінія) мають нормовану відстань від кінця до кінця$R/(b\sqrt{N}) \leq 1$.

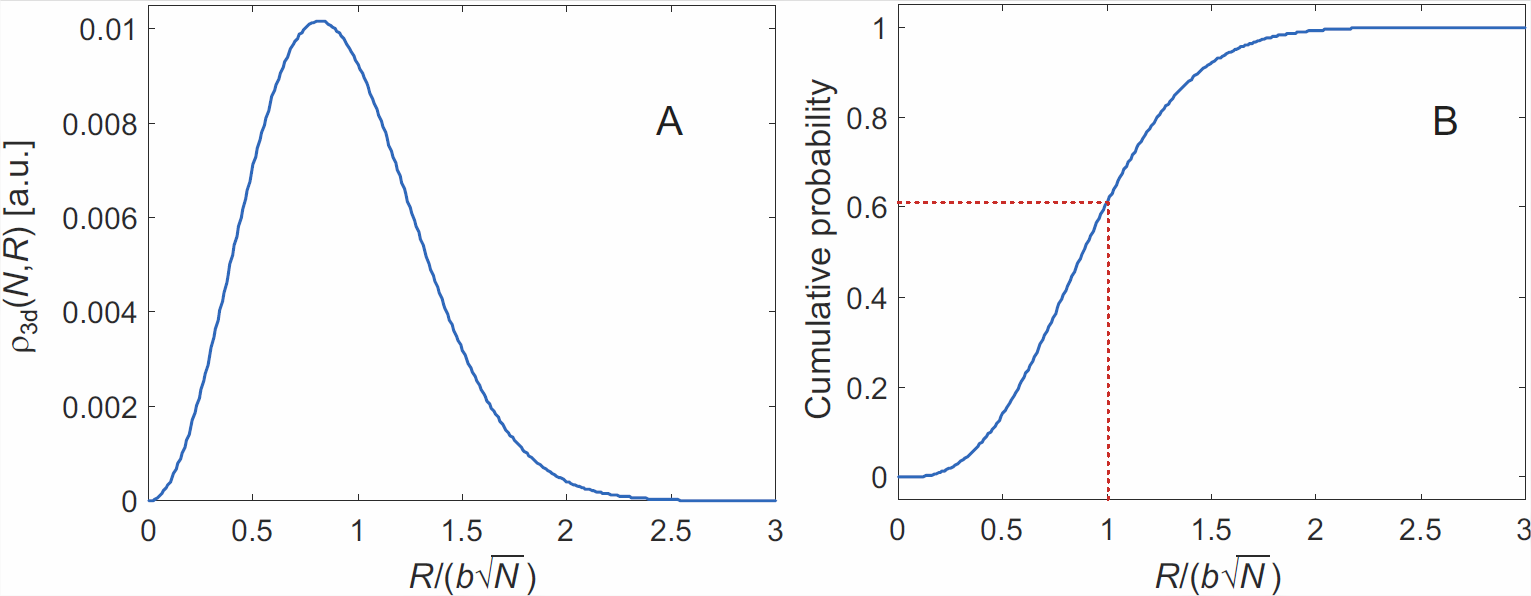
Нарешті, ми можемо поставити наступне питання: Якщо ми дозволимо всім ланцюжкам ансамблю починатися в одній точці, як кінці ланцюга розподіляються в просторі? Це найкраще зображено у сферичній системі координат. Симетрія диктує, щоб розподіл був рівномірним щодо полярних кутів$\theta$ і$\phi$. Полярна координата$R$ еквівалентна наскрізній відстані ланцюга. Щоб знайти розподіл ймовірностей для цієї наскрізної відстані, нам потрібно включити площу$4\pi R^2$ сферичних оболонок. Отже,

$$\rho_\mathrm{3d}(N,R) \cdot 4 \pi R^2 \mathrm{d} R = 4 \pi \left( \frac{3}{2 \pi N b^2} \right)^{3/2} \exp \left(-\frac{3 R^2}{2 N b^2} \right) R^2 \mathrm{d} R \ .$$

Через це масштабування з об'ємом нескінченно тонкої сферичної оболонки розподіл щільності ймовірності (рис.$\PageIndex{1A}$) для наскрізної відстані не пік на нульовій відстані. Як видно на малюнку$\PageIndex{1B}$, дуже навряд чи можна зіткнутися з ланцюгом с$R > 2b\sqrt{N}$. Так як довжина контуру є$R_\mathrm{max} = Nb$, можна зробити висновок, що при рівновазі майже всі ланцюги мають наскрізні відстані коротше, ніж$2 R_\mathrm{max} / \sqrt{N}$.

Потрібно обговорити достовірність результату, оскільки при апроксимуванні дискретного біноміального розподілу неперервним гаусовим розподілом ймовірностей ми зробили припущення$x \ll N$. В рамках ідеальної моделі ланцюга це припущення відповідає відстані від кінця до кінця, яка набагато коротша за довжину контуру$N b$. Якщо$R$ наближається$Nb$, то розподіл Гаусса завищує істинну щільність ймовірності. Насправді розподіл Гаусса пророкує невелику, але кінцеву ймовірність того, що ланцюг буде довшою за довжину її контуру, що є нефізичним. Модель може бути доопрацьована, включивши випадки такого сильного розтягування ланцюга. Для якісного обговорення ентропної еластичності не надто далеко від рівноваги, ми можемо задовольнитися рівнянням\ ref {eq:rho3d_chain}).

Конформаційна ентропія та вільна енергія

Тепер ми можемо поставити питання про залежність вільної енергії від розширення ланцюга$\vec{R}$. З визначенням ентропії Больцмана, Equation\ ref {eq:Boltzmann_entropy}) і звичайної ідентифікації$k = k_\mathrm{B}$ ми маємо

$$S(N,\vec{R}) = k_\mathrm{B} \ln \Omega(N,\vec{R}) \ .$$

Розподіл густини ймовірності в Equation\ ref {eq:rho3d_chain}) пов'язаний зі$\Omega$ статистичною вагою

$$\rho_\mathrm{3d}(N,\vec{R}) = \frac{\Omega(N,\vec{R})}{\int \Omega(N,\vec{R}) \mathrm{d} \vec{R}} \ ,$$

тому що$\rho_\mathrm{3d}$ це частка всіх конформацій, які мають наскрізний вектор в нескінченно малому інтервалі між$\vec{R}$ і$\vec{R} + \mathrm{d}\vec{R}$. Значить, ²²

$$\begin{align} S(N,\vec{R}) & = k_\mathrm{B} \ln \rho_\mathrm{3d}(N,\vec{R}) + k_\mathrm{B} \ln \left[ \int \Omega(N,\vec{R}) \mathrm{d} \vec{R} \right] \\ & = -\frac{3}{2} k_\mathrm{B} \frac{\vec{R}^2}{N b^2} + \frac{3}{2} k_\mathrm{B} \ln \left( \frac{3}{2 \pi N b^2} \right) + k_\mathrm{B} \ln \left[ \int \Omega(N,\vec{R}) \mathrm{d} \vec{R} \right] \ . \label{eq:s_N_R_ideal_chain}\end{align}$$

Останні два терміни не залежать$\vec{R}$ і, таким чином, складають внесок ентропії$S(N,0)$, який однаковий для всіх наскрізних відстаней, але залежить від кількості мономерів$N$,

$$S(N,\vec{R}) = -\frac{3}{2} k_\mathrm{B} \frac{\vec{R}^2}{N b^2} + S(N,0) \ .$$

Оскільки за визначенням сегменти Куна ідеальної ланцюга не взаємодіють один з одним, внутрішня енергія не залежить від$\vec{R}$. Таким чином, вільна енергія Гельмгольца$F(N,\vec{R}) = U(N,\vec{R}) - T S(N,\vec{R})$ може бути записана як

$$F(N,\vec{R}) = \frac{3}{2} k_\mathrm{B} T \frac{\vec{R}^2}{N b^2} + F(N,0) \ .$$

Звідси випливає, що вільна енергія окремого ланцюга досягає мінімуму при нульовому наскрізному векторі, згідно з нашим висновком у Розділі [subsect:random_walk], що щільність ймовірності максимальна для нульового наскрізного вектора. При довших наскрізних векторах ентропія ланцюга зменшується квадратично з довжиною вектора. Значить, ланцюг можна розглядати як ентропну пружину. Подовження пружини відповідає поділу кінців ланцюга на відстань$R \ll N b$. Сила, необхідна для цього подовження, є похідною вільної енергії Гельмгольца по відношенню до відстані. За один вимір отримуємо

$$f_x = -\frac{\partial F\left( N, \vec{R} \right)}{\partial R_x} = -\frac{3 k_\mathrm{B} T}{N b^2} \cdot R_x \ .$$

Для тривимірного випадку сила - це вектор, який є лінійним в$\vec{R}$,

$$\vec{f} = -\frac{3 k_\mathrm{B} T}{N b^2} \cdot \vec{R} \ ,$$

тобто ентропна весна задовольняє закон Гука. Константа ентропної пружини є$3 k_\mathrm{B} T/(Nb^2)$.

Таким чином, полімери тим легше розтягуються, чим більше їх ступінь полімеризації (пропорційна$N$), тим довше сегмент Куна$b$ і тим нижче температура$T$. Зокрема, температурна залежність є неінтуїтивною. Полімерний ланцюг під деформацією буде стискатися, якщо температура підвищена, так як ентропний внесок у вільну енергію Гельмгольца, яка протидіє деформації, потім збільшується.