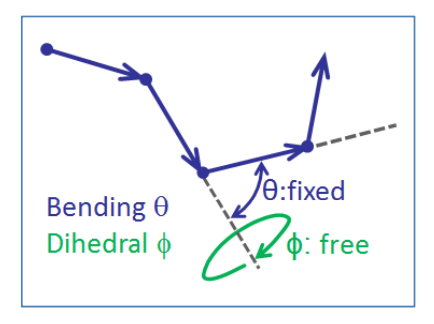
7.1: Сегментні моделі

Сегментні моделі ¹

• \((n + 1)\)намистини зв'язують\(n\) відрізками або зв'язками довжини\(\ell\).
• Кожна намистина має своє положення\(\vec{r_i}\).
• Кожному зв'язку присвоюється вектор,\(\vec{\ell_i} = \vec{r_i} - \vec{r_{i - 1}}\).
• Кут вигину між сусідніми сегментами\(i\) і\((i + 1)\) становить\(\theta_i\):\(\cos \theta = \vec{\ell_i} \cdot \vec{\ell_{i - 1}}\)
• Для кожного кута вигину існує пов'язаний двогранний кут, який\(\phi_i\) визначається як поворот сегмента за\((i+1)\) межі площини, визначеної сегментами\(i\) і\((i - 1)\).
• Розрізняють\(n - 1\) окремі згинальні і двогранні кути.

Статистичні змінні для макромолекул

Відстань від кінця до кінця

Довжина контуру - це повна довжина полімеру по контуру ланцюга:

\[L_C = n \ell\nonumber\]

Кожен ланцюг має однакову довжину контуру, але різні розміри в просторі, що є результатом конформаційної гнучкості. Первинною структурною змінною для вимірювання цієї конформаційної варіації є наскрізний вектор між першим і останнім\(\vec{R} = \vec{r_n} - \vec{r_0}\) кулькою, або еквівалентно

\[\vec{R} = \sum_{i = 1}^{n} \vec{\ell_i}\nonumber\]

Статистично розміри полімеру можна охарактеризувати статистикою наскрізної відстані. Розглянемо його середньоквадратичне значення:

\[\langle \vec{R}^2 \rangle = \langle \vec{R} \cdot \vec{R} \rangle = \left \langle \left (\sum_{i = 1}^{n} \vec{\ell_i} \right ) \cdot \left (\sum_{j= 1}^{n} \vec{\ell_j} \right ) \right \rangle\]

Після розширення цих сум ми можемо зібрати два набори термінів: (1) самовизначення з\(i = j\) і (2) міжзв'язкові кореляції\((i \ne j)\):

\[\begin{array} {rcl} {\langle \vec{R}^2 \rangle } & = & {n \ell^2 + \sum_{j \ne i} \langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle} \\ {} & = & {n \ell^2 + \ell^2 \sum_{j \ne i} \langle \cos \theta_{ij} \rangle} \end{array} \label{eq7.1.1}\]

\(\theta_{ij}\)Ось кут між відрізками\(i\) і\(j\). Цей другий термін описує будь-які можливі конформаційні переваги між сегментами по ланцюжку. Ми будемо називати множник\(\langle \cos \theta_{ij} \rangle\) кореляційною функцією орієнтації сегмента, яка також записується

\[\begin{array} {rcl} {g(k)} & = & {\langle \cos \theta_k \rangle} \\ {\theta_k} & = & {\vec{\ell_i} \cdot \vec{\ell_{i + k}} \ \ \ \ \ \ \ \ k = |j - i|} \end{array}\]

Тут\(k\) мається на увазі поділ між двома сегментами. Ця кореляційна функція може варіюватися за значенням від 1 до -1, де +1 представляє високо вирівняний або розширений ланцюг, а негативні значення будуть дуже стиснутими або компактними. Для розміщення сегментів випадковою прогулянкою не\((g = 0)\) передбачається жодних міжсмугових кореляцій.

Внутрішньозв'язкова кореляція може бути вставлена в сегментні моделі, як за допомогою спеціальних правил, так і шляхом застосування енергетичної функції, яка обмежує міжсегментні взаємодії. Наприклад, функція енергії кручення нижче\(U_{\text{conf}}\), буде використовуватися для зважування ймовірності того, що сусідні сегменти приймають певний кут кручення. Загальна функція енергії кручення\(U_{\text{conf}} (\Theta)\) включає всі\(2(n-1)\) можливі кути\(\Theta = \{\theta_1, \phi_1, \theta_2, \phi_2, ... \theta_{n-1}, \phi_{n-1} \}\), щільність ймовірності суглоба для прийняття певної конформації становить

\[P(\Theta) = \dfrac{e^{-U_{\text{conf}} (\Theta)/k_B T}}{\int d \Theta e^{-U_{\text{conf}} (\Theta)/k_B T}} \nonumber\]

Інтеграл над\(\Theta\) відображає\(2(n - 1)\) інтеграли над полярними координатами для всіх сусідніх відрізків,

\[\int d \Theta = \int_{0}^{\pi} \int_{0}^{2\pi} \sin \theta_1 d \theta_1 d \phi_1 \cdots \int_{0}^{\pi} \int_{0}^{2\pi} \sin \theta_{n - 1} d \theta_{n - 1} d \phi_{n - 1} \nonumber\]

Тоді функція кореляції вирівнювання

\[\langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 \int d \Theta \cos \theta_{ij} P (\Theta) \nonumber\]

Це не практична форма, тому зробимо спрощені припущення про форму такого розподілу ймовірностей. Наприклад, якщо конфігурація сегментів залежить тільки від найближчих сусідів\(P(\Theta) = P(\theta, \phi)^{(n - 1)}\).

Стійкість Довжина

Для будь-якого полімеру вирівнювання будь-якої пари векторів в ланцюжку стає некорельованим по досить довгій послідовності відрізків. Щоб кількісно оцінити цю відстань, ми визначаємо «довжину стійкості»\(\ell_p\).

\[\ell_p = \langle \hat{\ell_i} \cdot \sum_{j = 1}^{n} \vec{\ell_j} \rangle \ \ \ \ \hat{\ell_i} = \dfrac{\vec{\ell_i}}{|\ell |} \nonumber\]

Це характерна відстань по ланцюгу для розпаду для орієнтаційної кореляційної функції між векторами зв'язку,

\[g(k) = \ell ^2 \langle \cos^k \theta \rangle \nonumber\]

Як це буде вести себе? Якщо врахувати\(|\cos \theta | < 1\), що, то\(\langle \cos^k \theta \rangle \) буде падати зі збільшенням\(k\), наближаючись до нуля як\(k \to \infty\). Тобто пам'ять про вирівнювання між двома векторами зв'язку падає з їх поділом, де шкала відстані для втрати кореляції є\(\ell_p\). Таким чином, ми очікуємо монотонно розкладається форма цієї функції:

\[g(k) = \ell^2 e^{-k \ell / \ell_p} \label{eq7.1.3}\]

Для суцільних тонких стрижневих моделей полімеру цей вираз пишеться через контурну відстань\(s\), зміщення по контуру ланцюга\(s = \ell k\) (т. Е.

\[g(s) = \ell^2 e^{- |s|/\ell_p} \nonumber\]

Як ми ставимося\(\theta\) і\(\ell_p\)? ² Написання\(\langle \cos^k \theta \rangle \approx \exp (k \ln [\langle \cos \theta \rangle ])\) та прирівнювання цього до екв. (\(\ref{eq7.1.3}\)) вказує на те, що

\[\ell_p = -\ell \ln \langle \cos \theta \rangle \nonumber\]

Для жорстких ланцюгів ми можемо наблизити\(\ln (x) \approx (1 - x)\), так

\[\ell_p \approx \dfrac{\ell }{1 - \langle \cos \theta \rangle} \nonumber\]

Радіус обертання

Радіус обертання - ще одна важлива структурна змінна, яка тісно пов'язана з експериментальними спостережуваними. Тут розміри полімеру виражаються як розширення щодо центру мас для ланцюга.

Це виявляється корисним для розгалужених полімерів та гетерополімерів (таких як білки). Позначивши положення і масу\(i^{\text{th}}\) кульки як\(\vec{r_i}\) і\(m_i\), визначаємо центр маси для полімеру як середньозважений по масі положення кульок в просторі:

\[\vec{R_0} = \dfrac{\sum_{i = 0}^{n} m_i \vec{r_i}}{\sum_{i = 0}^{n} m_i} \nonumber\]

Індекс суми, що починається з 0, призначений для відображення суми над\(n+1\) намистинами. Знаменником цього виразу є загальна маса полімеру\(M = \sum_{i = 0}^{n} m_i\). Якщо всі намистини мають однакову масу, то\(m_i/M = 1/(n + 1)\) і\(R_0\) є геометричним середнім їх положенням.

\[\vec{R_0} = \dfrac{1}{n + 1} \sum_{i = 0}^{n} \vec{r_i}\nonumber\]

Радіус обертання\(R_G\) для конфігурації полімеру описує масово зважений розподіл кульок\(R_0\) і визначається через

\[\langle R_G^2 \rangle = \dfrac{1}{n + 1} \sum_{i = 0}^n \langle \vec{S_i^2} \rangle \nonumber\]

де\(\vec{S_i}\) радіус обертання, тобто радіальна відстань\(i^{\text{th}}\) кульки від центру маси

\[\begin{array} {rcl} {\vec{S}_i^2 = \dfrac{m_i }{M} (\vec{r_i} - \vec{R}_0)^2} & \ & {\text{(mass-weighted)}} \\ {\vec{S}_i^2 = \dfrac{1}{n + 1} (\vec{r_i} - \vec{R}_0)^2} & \ & {\text{(equal mass beads)}} \end{array}\nonumber\]

Крім того, ми можемо показати, що середній квадрат радіус обертання пов'язаний із середнім поділом всіх бісерин ланцюга.

\[\langle R_G^2 \rangle = \dfrac{1}{(n + 1)^2} \sum_{i = 0}^n \sum_{j = 0}^n \langle (\vec{r_i} - \vec{r_j})^2 \rangle \nonumber\]

Вільно з'єднаний ланцюг

Вільно з'єднана ланцюг описує макромолекулу як кістяк, для якого всі\(\phi\) можливі\(\theta\) і однаково вірогідні, і немає кореляцій між сегментами. Він відомий як «ідеальний ланцюг», оскільки між намистинами немає взаємодій або виключеного обсягу, а конфігурація полімерного хребта слідує за випадковою ходьбою. Якщо ми розмістимо першу намистину на\(r = 0\), ми виявимо\(\langle R \rangle = 0\), що, як і очікувалося для випадкової прогулянки, і екв. (\(\ref{eq7.1.1}\)) Зводить до

\[\langle R^2 \rangle = n \ell^2 \nonumber\]

\[\text{ or } R_{rms} = \langle R^2 \rangle^{1/2} = \sqrt{n} \ell \nonumber\]

Хоча середня відстань від кінця до кінця може дорівнювати нулю, дисперсія в наскрізному розподілі дорівнює

\[\sigma_r = \sqrt{\langle R^2 \rangle - \langle R \rangle^2} = \sqrt{n} \ell \nonumber\]

Радіус обертання для ідеального ланцюга дорівнює:

\[R_G = \sqrt{\dfrac{\langle R^2 \rangle }{6}} = \sqrt{\dfrac{n \ell^2}{6}}\nonumber\]

Гаусова випадкова котушка

Вільно з'єднаний ланцюг також відомий як гаусова випадкова котушка, оскільки статистика її конфігурації повністю описується\(\langle R \rangle\) і\(\langle R^2 \rangle\), перші два моменти гауссового наскрізного розподілу ймовірностей\(P(R)\). Наскрізну щільність ймовірності в одному вимірі можна отримати з випадкової ходьби з\(n\) однаково розмірними кроками довжини\(\ell\) в одному вимірі, де однаково вірогідні кроки вперед і назад. Якщо перша намистина у нього\(x_0 = 0\) встановлена, то остання намистина укладається останнім кроком в положенні\(x\). У безперервному ліміті:

\[P(x, n) = \sqrt{\dfrac{1}{2\pi n \ell^2}} e^{-x^2/2n \ell^2}\label{eq7.1.4} \]

\(P(x, n) dx\)це ймовірність знаходження кінця ланцюжка з\(n\) намистинами на відстані між\(x\) і\(x+dx\) від її першої намистини. Зверніть увагу, що це прирівнює середньоквадратичну відстань до кінця зі стандартним відхиленням для цього розподілу:\(\langle R^2 \rangle = \sigma^2 = n \ell^2\).

Узагальнити eq. (\(\ref{eq7.1.4}\)) до тривимірного ланцюга, ми визнаємо, що поширення в\(x, y\), і\(z\) розміри однаково вірогідні, так що щільність ймовірності 3D може бути отримана з добутку щільності ймовірності 1D\(P(r) = P(x) P(y) P(z)\). Крім того, нам потрібно врахувати обмеження, що розподіл наскрізних відстаней однаковий у кожному вимірі:

\[\langle \vec{R}^2 \rangle = \sigma_x^2 + \sigma_y^2 + \sigma_z^2 = n \ell^2 \nonumber\]

і з тих пір\(\sigma_x^2 = \sigma_y^2 = \sigma_z^2\),

\[\langle \vec{R}^2 \rangle = 3 \sigma_x^2 = n \ell^2 \nonumber\]

Тому,

\[\begin{array} {rcl} {P(r, n)} & = & {\sqrt{1}{2\pi \sigma_x^2} e^{-x^2/2 \sigma_x^2} \sqrt{1}{2\pi \sigma_y^2} e^{-x^2/2 \sigma_y^2} \sqrt{1}{2\pi \sigma_z^2} e^{-x^2/2 \sigma_z^2} } \\ {} & = & {\left (\dfrac{3}{2\pi \sigma^2} \right )^{3/2} e^{-3r^2/2\sigma^2}} \end{array} \nonumber\]

Для спрощення визначено параметр масштабування з розмірами зворотної довжини

\[\beta = \sqrt{\dfrac{3}{2n \ell^2}} = \sqrt{\dfrac{3}{2}} \langle R^2 \rangle^{-1/2} \nonumber\]

Потім щільність ймовірності в декартових координатах,

\[P(x, y, z, n) = \dfrac{\beta^3}{\pi^{3/2}} e^{-\beta^2 r^2} \ \ \ \text{ where } r^2 = x^2 + y^2 + z^2 \nonumber\]

Зверніть увагу, що одиниці\(P(x, y, z, n)\) - це зворотний об'єм або концентрація. Імовірність знаходження кінця ланцюжка з\(n\) бісеру в коробці об'ємом dx dy dz в положенні\(x, y, z\) дорівнює\(P(x, y, z, n)\ dx\ dy\ dz\). Ця функція ілюструє, що найбільш ймовірна відстань від кінця до кінця для випадкового полімеру ходьби знаходиться на початку. З іншого боку, ми також можемо висловити це як радіальну щільність ймовірності, яка дає ймовірність знаходження кінця ланцюга в радіусі між\(r\) і\(r+dr\) від початку. Так як обсяг сферичної оболонки зростає пропорційно площі її поверхні:

\[P(r, n) dr = 4 \pi r^2 P(x, y, z, n) dr\nonumber\]

\[P(r, n) = 4\pi r^2 \left (\dfrac{3}{2\pi n \ell^2} \right )^{3/2} \exp \left [-\dfrac{3}{2} \dfrac{r^2}{n \ell^2} \right ]\]

Одиниці\(P(r, n)\) - зворотна довжина. Для вільно з'єднаної ланцюга ми бачимо, що\(\beta^{-1} = \sqrt{2\langle R^2 \rangle /3}\) це найбільш вірогідна відстань впритул.

Вільно обертається ланцюг

Розширення до вільно з'єднаного ланцюга, що додає єдине конфігураційне обмеження, яке краще нагадує справжнє склеювання в полімерах, - це вільно обертається ланцюг. При цьому кут хребта\(\theta\) має фіксовану величину, а двогранний кут\(\phi\) може вільно обертатися.

Для опису розмірів ланцюга нам потрібно оцінити кутові зв'язкові кореляції між сегментами. Орієнтуючись спочатку на сусідні сегменти, ми знаємо\(\phi\), що після усереднення по всьому фіксований\(\theta\) гарантує це\(\langle \vec{\ell_i} \cdot \vec{\ell_{i+1}} \rangle = \ell^2 \cos \theta\). Для наступного сегмента в серії лише компонент, паралельний до,\(\vec{\ell_{j + 1}}\) сприятиме послідовним зв'язкам, як ми усереднюємо\(\phi_{i + 2}\):

\[\begin{array} {rcl} {\langle \vec{\ell_i} \cdot \vec{\ell_{i + 2}} \rangle} & = & {\langle \cos (\theta_i) \cos (\theta_{i + 1}) - \sin (\theta_i) \sin (\theta_{i + 1}) \cos (\phi_{i + 1}) \rangle} \\ {} & = & {\ell^2 \cos^2 \theta} \end{array}\nonumber\]

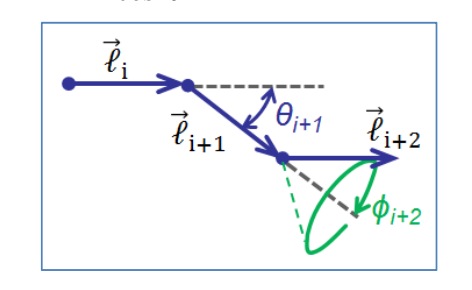
Розширення цього міркування призводить до спостереження

\[\langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 (\cos \theta)^{j - i} \nonumber\]

Для оцінки зв'язкових кореляцій у цьому виразі корисно визначити індекс поділу між двома векторами зв'язків:

\[k = j - i\nonumber\]

і

\[\alpha = \cos \theta \nonumber\]

Тоді функція кореляції орієнтації сегмента

\[g(k) = \langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 \alpha^k \nonumber\]

Для поділу\(k\) на ланцюжку довжини\(n\)\(n-k\) можливі комбінації кутів зв'язку,

\[\sum_{j \ne i} \langle (\cos \theta)^{j - i} \rangle = \sum_{k = 1}^{n - 1} (n - k) \alpha^k \nonumber\]

\[\therefore \ \ \ \ \ \langle R^2 \rangle = n \ell^2 + \ell^2 \sum_{k = 1}^{n - 1} (n - k) \alpha^k \nonumber\]

З цього можна отримати

\[\langle R^2 \rangle = n \ell^2 \left (\dfrac{1 + \alpha}{1 - \alpha} - \dfrac{2\alpha (1 - \alpha^n)}{n (1 - \alpha)^2} \right ) \nonumber\]

У межі довгих ланцюгів (\(n \to \infty\)) знаходимо

\[\langle R^2 \rangle \to n \ell^2 \left ( \dfrac{1 + \alpha}{1 - \alpha} \right )\nonumber\]

і

\[R_G = \sqrt{\dfrac{n \ell^2}{6} \left ( \dfrac{1 + \alpha}{1 - \alpha} \right )}\nonumber\]

Обмежені дигідралі

Коли вільно обертається ланцюг також змінюється, щоб обмежити двогранний кут\(\phi\), ми можемо вирішити середню квадратну відстань від кінця до кінця в межі\(n \to \infty\). З огляду на середній двогранний кут,

\[\beta = \langle \cos \phi \rangle \nonumber\]

\[\langle R^2 \rangle = n \ell^2 \left (\dfrac{1 + \alpha}{1 - \alpha} \right ) \left (\dfrac{1 + \beta}{1 - \beta} \right ) \nonumber\]

Неідеальна поведінка

Співвідношення характеристик флори

Справжні полімери жорсткі і виключають обсяг, але поведінка\(R \sim \sqrt{n}\) масштабування зазвичай тримається на великих розмірах\(n (R \gg \ell_p)\). Для характеристики неідеальності скористаємося характеристичним співвідношенням Флорі:

\[C_n = \dfrac{\langle R^2 \rangle}{n \ell^2} \nonumber\]

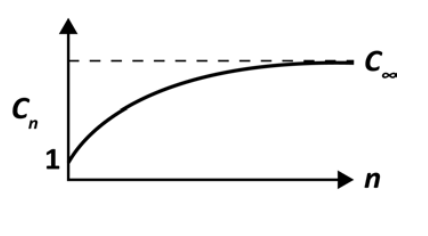
Для вільно з'єднаних ланцюгів\(C_n = 1\). Для неідеальних ланцюгів з кутовими кореляціями,\(C_n > 1\). Cn залежить від довжини ланцюга\(n\), але повинен мати асимптотичне значення для великих\(n\):\(C_{\infty}\). Наприклад, якщо розглядати довгі вільно обертаються ланцюга

\[C_{\infty} = \lim_{n \to \infty} \dfrac{\langle R^2 \rangle}{n \ell^2} = \dfrac{1 + \alpha}{1 - \alpha} \ \ \ \ \ \alpha = \cos \theta \nonumber\]

(На практиці ця межа зазвичай дотримується\(n > 30\)). Розглянемо чотиригранно пов'язаний полімер з повним кутом\(109^{\circ}\) (\(\theta = 54^{\circ}\)). потім\(\cos \theta = 1/3\), і\(C_n = 2\). На практиці ми досягаємо межі довгого ланцюга\(C_{\infty}\) на\(n \approx 10\). Це співвідношення добре працює для полігліцину і поліетиленгліколю (ПЕГ).

Статистичний відрізок або довжина Куна

Наскільки жорсткий або гнучкий полімер, залежить від довжини шкали спостереження. Те, що жорстке в одній шкалі, є гнучким для іншого. Для нескінченно довгого полімеру завжди можна знайти шкалу довжини, для якої його статистика є статистикою гаусової випадкової котушки. В результаті для сегментного полімеру можна уявити масштаб безперервних сегментів на один більш довгий «ефективний сегмент», який може не представляти атомних розмірів, а скоріше визначається для того, щоб відповідати випадковому полімеру ходьби, з\(C_n = 1\). Потім ефективна довжина сегмента\(\ell_e\) (також відома як довжина Куна), а кількість ефективних сегментів -\(n_e\). Тоді застосовуються вільно з'єднані рівняння ланцюга:

\[\begin{array} {c} {L_C = n_e \ell_e} \\ {\langle R^2 \rangle = n_e \ell_e^2} \end{array} \nonumber\]

З цих рівнянь,\(\ell_e = \langle R^2 \rangle /L_C\). Ми бачимо, що\(\ell_e \gg \ell\) стосується жорстких ланцюгів, тоді як\(\ell_e \approx \ell\) гнучкі.

Ми також можемо записати довжину контуру як\(L_C = \gamma n \ell\), де\(\gamma\) геометричний коефіцієнт < 1, який описує обмеження на кути зв'язку. Для вільно обертається ланцюга:\(\gamma = \cos (\theta /2)\). Використовуючи вирази довгого ланцюга ланцюга\((n \to \infty)\):\(\langle R^2 \rangle = C_{\infty} n \ell^2\), знаходимо

\[\begin{array} {c} {\ell_e = \left (\dfrac{C_{\infty}}{\gamma } \right ) \ell} \\ {n _{\ell} = \left (\dfrac{\gamma^2}{C_{\infty}} \right ) n} \\ {\ell_p = \left (\dfrac{C_{\infty} + 1}{2} \right ) \ell } \end{array} \nonumber\]

Представницькі значення для моделей полімерних сегментів

	\(C_{\infty}\)	\((n_e/n)\)	\(\ell\)(нм)	\(\ell_e\)(нм)	\(\gamma\)	\(\ell_p\)(нм)
Поліетилен	\ (C_ {\ infty}\) ">6.7	\ ((n_e/n)\) "> (n > 10)	\ (\ ell\) (нм) ">0.154	\ (\ ell_e\) (нм) ">1.24	\ (\ гамма\) ">0.83	\ (\ ell_p\) (нм) ">
КІЛОЧОК	\ (C_ {\ infty}\) ">3.8	\ ((n_e/n)\) ">	\ (\ ell\) (нм) ">	\ (\ ell_e\) (нм) ">0.34	\ (\ гамма\) ">	\ (\ ell_p\) (нм) ">
Поліаланін	\ (C_ {\ infty}\) ">9	\ ((n_e/n)\) "> (n > 70)	\ (\ ell\) (нм) ">0.38	\ (\ ell_e\) (нм) ">3.6	\ (\ гамма\) ">0,95	\ (\ ell_p\) (нм) ">0.5
Поліпролін	\ (C_ {\ infty}\) ">90	\ ((n_e/n)\) "> (n > 700)	\ (\ ell\) (нм) ">	\ (\ ell_e\) (нм) ">	\ (\ гамма\) ">	\ (\ ell_p\) (нм) ">5-10
dsDNA	\ (C_ {\ infty}\) ">86	\ ((n_e/n)\) ">	\ (\ ell\) (нм) ">0,35	\ (\ ell_e\) (нм) ">30-100	\ (\ гамма\) ">1	\ (\ ell_p\) (нм) ">50
SSDNA	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (нм) ">	\ (\ ell_e\) (нм) ">	\ (\ гамма\) ">	\ (\ ell_p\) (нм) ">1.5
Целюлоза	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (нм) ">	\ (\ ell_e\) (нм) ">	\ (\ гамма\) ">	\ (\ ell_p\) (нм) ">6.2
Актин	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (нм) ">	\ (\ елл_е\) (нм) ">16700	\ (\ гамма\) ">	\ (\ ell_p\) (нм) ">10000-20000

____________________________________________

1. Кантор і П.Р. Шіммель, Біофізична хімія Частина III: Поведінка біологічних макромолекул. (Фрімен, Сан-Франциско, 1980), гл. 18; К. Ділл і С.Бромберг, Молекулярні рушійні сили: Статистична термодинаміка в біології, хімії, фізиці та нанонауці. (Тейлор і Френсіс Груп, Нью-Йорк, 2010); П.Дж. Флорі, Принципи хімії полімерів. (Корнельська університетська преса, Ітака, 1953).
2. Кантор і П.Р. Шіммель, Біофізична хімія Частина III: Поведінка біологічних макромолекул. (У.Х. Фрімен, Сан-Франциско, 1980), гл. 19 с. 1033.