Skip to main content
LibreTexts - Ukrayinska

4.9: Модуль, температура, час

  1. Last updated
  2. Save as PDF
  • Page ID
    19918

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Модуль зберігання вимірює опір деформації в пружному твердому тілі. Це пов'язано з постійною пропорційності між стресом і деформацією в законі Гука, який стверджує, що розширення збільшується з силою. У динамічному механічному аналізі ми дивимося на напругу (σ), яка є силою на одиницю площі поперечного перерізу, необхідною для того, щоб викликати розширення в зразку, або деформацію (ε).

    \[E = \dfrac{σ}{ ε}\]

    Крім того, в експерименті зі зсувом:

    \[G = \dfrac{σ}{ε}\]

    Динамічний механічний аналіз відрізняється від простого випробування на розтяг проведенням експерименту циклічно. Зразок розтягується і звільняється (або стрижеться і відпускається). Потім його можна піддати додатковому навантаженню і знову звільнити. Тут задіяний елемент часу. Зокрема, оскільки експеримент є циклічним, його можна проводити на різних частотах. Коли ви це зробите, і ви будуєте отриманий модуль проти частоти, ви можете отримати додаткову інформацію про зразок. Результати, як правило, будуть представлені на графіку, подібному до цього:

    CPDMAfreq.png

    Графік говорить нам про те, що частота чітко має значення. Коли експеримент виконується на більш високих частотах, модуль зберігання вище. Матеріал здається більш жорстким. Навпаки, модуль втрат нижчий на цих високих частотах; матеріал поводиться набагато менше, як в'язка рідина. Зокрема, різке падіння модуля втрат пов'язане з часом релаксації матеріалу. У цьому контексті саме цей час потрібен ланцюгам, щоб перетікати в нові конформації у відповідь на прикладене напруження. Якщо вони не встигнуть витікати, то ця в'язка реакція матеріалу втрачається. Матеріал поводиться набагато більше як пружне тверде тіло при підданні високочастотної циклічної деформації. Це важливо знати, тому що матеріал може піддаватися вібраціям або іншим стимулам під час щоденного використання, і його властивості можуть відповідно змінюватися.

    Ще одна варіація такого роду експерименту називається динамічним механічним термічним аналізом. Замість того, щоб змінювати частоту подразника протягом усього експерименту, частота тримається постійною, а температура змінюється замість цього. В результаті ми можемо знову побачити, як матеріал реагує в різних умовах, що може сказати нам, як він буде вести себе в повсякденному застосуванні. Результатом експерименту може бути графік, подібний до наведеного нижче:

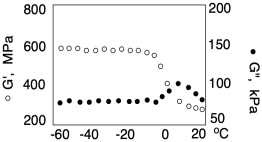
    CPDMA.png

    На даний момент ви вже знайомі зі скляним переходом. Не варто дивуватися, що властивості залежать від температури. При температурі скляного переходу розширюється обсяг матеріалу зі збільшенням температури стає достатнім для забезпечення ланцюгового потоку. В результаті матеріал раптом поводиться набагато більше, як в'язка рідина. Збільшується модуль втрат. Жорсткість матеріалу падає, оскільки заплутані ланцюги вже не так сильно протистоять деформації. Модуль зберігання зменшується.

    Таким чином, динамічний механічний термічний аналіз забезпечує альтернативний спосіб визначення температури скляного переходу. Оскільки він насправді вимірює інше фізичне явище, ніж диференціальна скануюча калориметрія, T g, отриманий в результаті експерименту DMTA, може не точно погодитися з одним, отриманим в результаті експерименту DSC. Проте часто корисно мати різні способи оцінки властивостей.

    Для полегшення аналізу T g в цьому експерименті зазвичай відображається інша кількість. Tan delta - це всього лише відношення модуля втрат до модуля зберігання. Він пік при температурі скляного переходу.

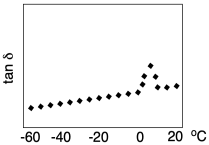
    CPDMAtandelta.png

    Термін «дельта засмаги» відноситься до математичної обробки модуля зберігання; це те, що відбувається в фазі з (або одночасно з) застосуванням напруги, тоді як модуль втрат відбувається поза фазою із застосуванням напруги. Оскільки це займе деякий час, щоб ланцюги перейшли в нове підтвердження, коли вони піддаються стресу, деформація фактично відстає від напруги в цих експериментах.

    CPstresstraintimelag.png

    Дельта відноситься до фазового відставання, кількості часу між прикладанням напруги та спостереженням максимальної деформації. Ви можете пам'ятати, що крива синуса і крива косинуса знаходяться поза фазою один з одним. Модуль зберігання описується як пропорційний cos δ, тоді як модуль втрат пропорційний sinδ. Ставлення cosδ до sinδ якраз tanδ.

    Чому tanδ пік при температурі склопереходу? Зрозуміло, що в міру того, як ланцюги починають рухатися вільніше, модуль втрат збільшується. Отже, матеріал також стає менш жорстким і більш гумовим. Модуль зберігання падає. Якщо tan delta - це відношення модуля втрат до модуля зберігання, він повинен збільшитися в цей момент - і це відбувається. Чому він знову падає? Це тому, що модуль втрат відноситься до втрати енергії, але оскільки матеріал став м'якшим, менше напруження (і менше енергії) вводиться в зразок в першу чергу, тому втрати енергії також стають меншими. Як результат, дельта засмаги піднімається на скляному переході, але знову падає незабаром за цю точку.

    Проблема РР9.1.

    Оцініть зберігання і втрати, модуль пружності в склоподібній фазі і гумову фазу в кожному з наступних випадків.

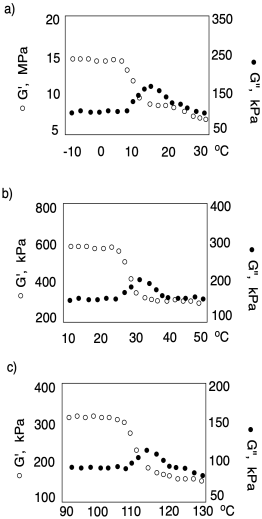
    CPdmtaQ.png

    Проблема РП9.2.

    Оцініть T g в кожному з наступних випадків.

    CPDMAtandeltaQ.png