4.7: Відносини стрес-деформації

Якщо подумати про матеріали, виготовлені з полімерів, пара речей може легко прийти в голову. Ви можете подумати про повсюдне використання пластмас у конструкціях навколо нас, таких як автомобільні бампери. Ви можете подумати про гумку, яку ви використовуєте для кріплення чогось міцніше, або вдома, або в лабораторії. У будь-якому випадку функція матеріалу спирається на його реакцію на подразники. Ми хочемо, щоб він був гнучким, щоб змінити форму, але потім прив'язати назад до того, звідки вона взялася? Наскільки нам потрібно гнучкості? Де компроміс між гнучкістю і міцністю?

Ці питання важливі в хімії полімерів. Отже, нам часто потрібно досліджувати, як матеріали поводяться в різних умовах, щоб ми знали, як їх можна використовувати найбільш ефективно.

Випробування на розрив є одним з найпростіших способів зондування того, як матеріал реагує на напругу. Пам'ятайте, що напруга в цьому контексті означає силу, що чиниться на матеріал на одиницю площі поперечного перерізу. Як такий, він має одиниці тиску, такі як Паскаль (Па). Для проведення експерименту два кінці зразка прикріплюються до двох затискачів, один з яких є рухомим. Рухомий затискач потім натягується так, щоб зразок став розтягнутим. Реєструється сила, необхідна для витягування зразка і, враховуючи площу поперечного перерізу зразка перпендикулярно силі, зусилля перетворюється в одиниці деформації.

Експеримент також вимірює відстань, на яку проба розтягується (деформація). Ця відстань зазвичай виражається у вигляді співвідношення, порівнюючи зміну довжини з початковою довжиною зразка. Його можна записати або у вигляді дробу, або у відсотках.

На приблизному ескізі нижче ми бачимо, що зазвичай відбувається в такому експерименті. Зразок розтягується (напруга збільшується), і його стає важче розтягувати, як видно з зростаючої сили (і, отже, збільшення напруги), яка необхідна для його розтягування. Зрештою, напруга падає, через пробу розривається.

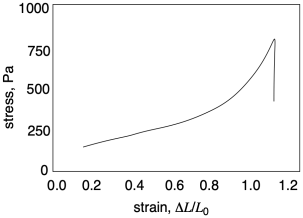
Вже на цьому графіку ми можемо побачити пару важливих частин інформації, яку ми можемо дізнатися з випробувань на розтяг. Номер один, наскільки ми можемо розтягнути цей матеріал, перш ніж він зламається? Ця кількість називається «штамом при розриві». У цьому зразку деформація при розриві виглядає приблизно на 1,1 або 110%; це означає, що зразок був розтягнутий до удвічі більшої початкової довжини, а потім деякої. Номер два, скільки напруги може підтримувати зразок, не порушуючи? Ця кількість називається «граничною міцністю на розрив». У цьому зразку гранична міцність на розрив становить трохи більше 750 Па.

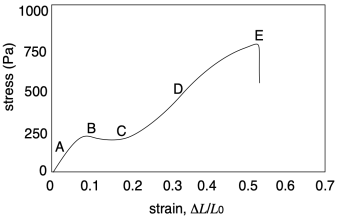
Якщо ми уважніше подивимося на графік з іншого зразка, то отримаємо третю важливу величину, і побачимо деякі додаткові можливості. Важливу величину можна вивести з першої частини кривої (А), в якій напруга зростає лінійно з деформацією. У цьому лінійному регіоні матеріал поводиться як «хукеанське тверде тіло», тобто він підпорядковується Закону Гука. Закон Гука говорить, що стрес і напруга повинні бути прямо пропорційними. У його оригінальних словах розширення пропорційно силі:

F = кс

в якому F - сила, x - розширення твердого тіла, а k - константа пропорційності.

Закон Гука зазвичай застосовується до поведінки механічних пружин, але він також стосується інших твердих матеріалів. Нахил у лінійній області графіка (A) дорівнював би цій константі пропорційності, k, оскільки графік показує співвідношення F/x. У матеріалознавстві цей схил частіше називають «модулем Юнга». Вона є мірою властивої матеріалу жорсткості.

Модуль Юнга: E = σ /ε

в якому σ = напруга і ε = розтяжна деформація.

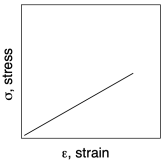
Розширювальна деформація - це лише деформація, що спостерігається при розтягуванні матеріалу. На графіку, показаному вище, модуль Юнга знаходиться навколо:

250 Па/0,1 = 2500 Па.

Цю початкову область кривої, в якій підкоряється Закону Гука, іноді називають «лінійною пружною областю». Слово «еластичний» має безпосередній відтінок у повсякденній англійській мові, приводячи до уваги гумку, яку можна розтягнути, тому ми думаємо про розтягуючу частину, коли чуємо слово «еластичний». Однак зворотний рух є важливою особливістю еластичної поведінки. Гумка завжди повертається до первісної форми. Так само в межах лінійної еластичної області будь-який твердий матеріал повертається до початкової форми після того, як він деформується під напругою.

З більшістю твердих речовин, таких як алюміній або бетон, лінійна пружна область охоплює дуже вузький діапазон деформацій. Просто подивившись, ми б не помітили, що ці матеріали деформуються. Однак ця лінійна залежність напруження-деформація характерна для твердих тіл. У реології така поведінка описується як еластична. Звичайно, з багатьма полімерами зразок може бути розтягнутий настільки, що ви можете побачити зміни неозброєним оком, і він все одно повертається до тієї первісної форми.

Чим відрізняються полімери? Довголанцюгова структура полімерів змушує їх поводитися інакше, ніж інші матеріали. Ці ланцюги можуть зазнавати конформаційні зміни: кожна зв'язок уздовж ланцюга може обертатися, перетворюючи полімерну ланцюг в трохи іншу форму. Ця здатність надає «м'якому матеріалу» велику гнучкість. Конформації ланцюгів можуть адаптуватися до напруги, переміщуючи ланцюги в нові форми, які пропонують упаковку з меншою енергією між собою. Коли напруга знімається, ланцюги врешті-решт ковзають назад у свої початкові конформації. Вони повертаються до своїх рівноважних форм.

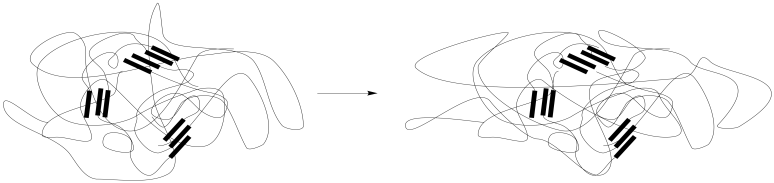
Наявність фізичних або хімічних зшивальних зв'язків допомагає матеріалу повернутися до початкової форми, функціонуючи як опорні точки, щоб ланцюги не збивалися занадто далеко. Ці взаємодії можуть бути знайдені в жорсткофазних взаємодіях у матеріалі, розділеному мікрофазою, як показано тут, хоча вони також можуть бути знайдені в однорідному матеріалі.

Лінійна пружна область - це не все, що ми бачимо в кривій напруження-деформації вище. У точці (B) лінійна залежність раптово втрачається. Стрес може навіть впасти, як це видно в цьому конкретному випадку. Ця ознака на графіку називається «точкою плинності». Напруга, яку відчуває матеріал, і результуюча деформація стали достатніми для подолання природної еластичної поведінки твердого тіла. Як зазначалося раніше, фізичні зшивання, такі як водневі зв'язки, допомагають посилити еластичну поведінку зразка полімеру. Якщо в якийсь момент ці взаємодії будуть подолані, ланцюги почнуть легше ковзати один за одного.

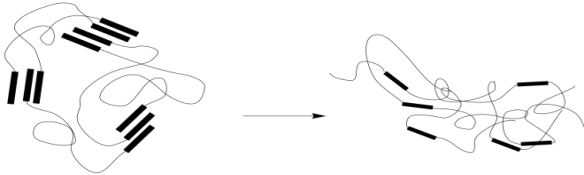
В результаті матеріал втрачає еластичність. Коли напруга звільняється, матеріал все одно пружиниться назад, коли ланцюги осідають у нову конформаційну рівновагу. Однак ця рівновага не буде такою ж, як раніше. Нові фізичні зшивання утворюватимуться, коли групи утворюють міжмолекулярні взаємодії з найближчими сусідами, з якими вони стикаються. Малоймовірно, що це завжди будуть ті ж групи, з якими вони взаємодіяли раніше. В результаті матеріал осяде трохи іншу форму. Ви, напевно, бачили, як це сталося раніше, коли гумка була розтягнута занадто далеко, занадто часто або занадто довго. Ланцюги відкинули свої старі взаємодії і підібрали нові, які легше формувалися в розширеній формі.

У точці (С) графіка прикладу нахил кривої починає збільшуватися. Така ж зміна напруги призводить до менших і менших змін деформації; матеріал стає жорсткішим. Це явище називається «деформаційне загартовування». Ця особливість не завжди спостерігалася б, але якби це сталося, чим би це пояснити? У полімерів одне пояснення може полягати в тому, що обсяг матеріалу повинен залишатися постійним у міру його розтягування. Якщо зразок стає довшим, це означає, що він також стає все вужчим.

Внаслідок цього звужується поперечний переріз, ланцюги стискаються між собою. У якийсь момент між сусідніми ланцюгами починають виникати фізичні зшивання. Ці зшивання не відбуваються в рівноважних положеннях, з полімерними ланцюгами, згорнутими навколо один одного, як вони були в оригінальному зразку. Ці зшивання виникають, коли ланцюги витягнуті, що лежать паралельно один одному, на більш близьких контактних відстанях, ніж зазвичай.

Ми можемо бачити протилежний вид речі відбувається в (D), коли нахил кривої зменшується замість збільшення. Це явище називається «розм'якшення штаму». Знову ж таки, це може спостерігатися не у всіх зразках. Коли це відбувається, що викликає це? У цьому випадку відповідь простіше. Подолавши взаємодії, які утримували ланцюги разом, нічого не залишається, щоб протистояти подальшій деформації. У міру того, як ланцюги починають розплутуватися один від одного, їх стає ще легше витягувати, полегшуючи розгинання або розтягування зразка.

Зрештою, в точці розриву (Е) ланцюги починають втрачати контакт один з одним в деякому місці зразка, в результаті чого відбувається катастрофічний розрив зразка.

Проблема ПП7.1.

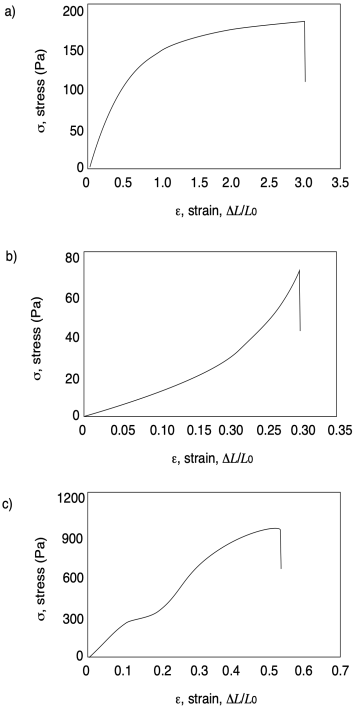
У кожній з наступних кривих оцініть граничну міцність на розрив і деформацію при розриві.

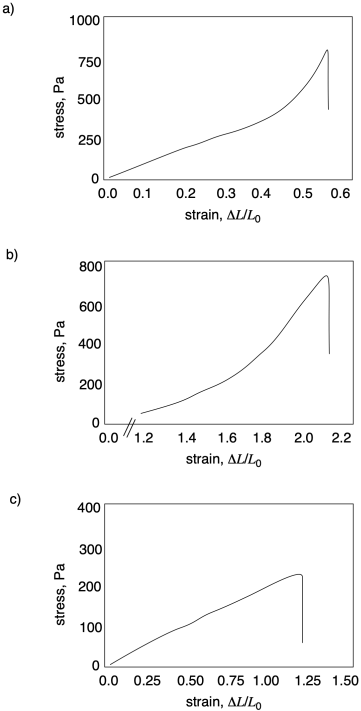
Проблема ПП7.2.

У кожній з наступних кривих обчислити модуль Юнга.

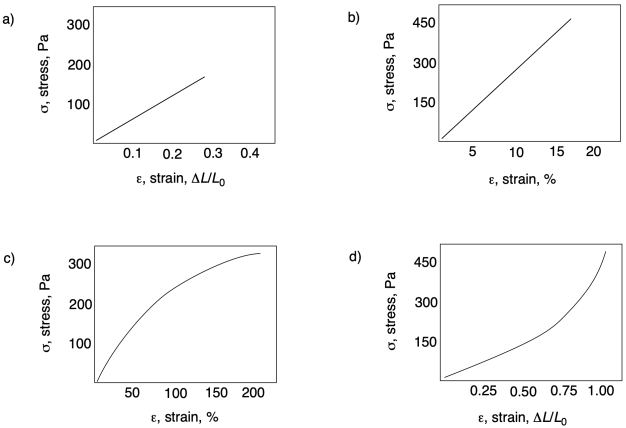
Проблема п.7.3.

У кожній з наступних кривих визначте будь-які діагностичні особливості.