4.10: Розділ 3 Рішення

Last updated
Save as PDF

Page ID: 19951

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Проблема ПП1.1.

а) При більш короткому часі елюції I має більш високу молекулярну масу, ніж II. Більш вузький пік означає, що I має більш вузьку дисперсність, ніж II.

б) При більш короткому часі елюції III має більш високу молекулярну масу, ніж IV. Більш широкий пік означає, що III має більш широку дисперсність, ніж IV.

в) При більш високому часі елюції V має меншу молекулярну масу, ніж VI. Більш широкий пік означає, що V має більш широку дисперсність, ніж VI.

Проблема ПП1.2.

а) одиниця повторення: 109 х (С ₄ Н ₆ О ₂) = 109 х 86.09 г/моль = 9,383,81 г/моль

кінцеві групи: С ₉ Н ₁₁ + Бр = 119,19+ 79,9 = 199,09 г/моль

всього: 9,383,81 + 199.09 = 9,582,90 г/моль

б) одиниця повторення: 763 х (С ₈ Н ₈) = 763 х 104,15 г/моль = 79,466,45 г/моль

кінцеві групи: С ₄ Н ₉ + Н = 57,12 + 1,008 = 58,13 г/моль

всього: 79,466,45 + 58,13 = 79,524,58 г/моль

в) одиниця повторення: 48 х (C ₄ H ₆ O ₂) = 48 х 86.09 г/моль = 4,132,32 г/моль

кінцеві групи: С ₄ Н ₉ + С ₇ Н ₅ S ₂ = 57,12+ 153,26 = 210,38 г/моль

всього: 4,132,32 + 210,38 = 4 342,70 г/моль

Проблема ПП1.3.

Ставлення інтеграла одиниці повторення на протон до кінцевої групи протона на інтеграл дає ступінь полімеризації. Ми могли б взяти всю інтеграцію кінцевої групи і розділити її на всю кількість протонів у цій групі, або вибрати одну позицію для представлення кінцевої групи. Аналогічно, ми можемо вибрати одну позицію для представлення одиниці повторення.

а) повторити одиницю інтеграла на протон = 36,0/2H = 18

інтеграл кінцевої групи на протон = 0,32/ 2H = 0,16

ступінь полімеризації = 18/0,16 = 112

б) повторити одиницю інтеграла на протон = 26,0/1Н = 26

інтеграл кінцевої групи на протон = 1,32/ 9Н = 0,15

ступінь полімеризації = 26/0,15 = 173

в) повторити одиницю інтеграла на протон = 54,0/4H = 13,5

інтеграл кінцевої групи на протон = 0,49/ 1Н = 0,49

ступінь полімеризації = 13,5/0,49 = 28

Проблема ПП2.1.

α - нахил, який є [підйом]/[біг]. Ось приблизно [4,0-2,4]/[6,6-4,4] = 1,6/2,2 = 0,73.

K - y-перехоплення. Рівняння для прямої лінії y = mx +b; у цьому випадку y = 0.73x+ b Якщо ми виберемо точку на прямій, наприклад (x, y) = (4.9, 2.0), ми можемо замінити ці значення на x і y, щоб отримати b.

Так 2,0 = 0,73 (4,9) + б, або б = 2,0 - 3,56 = -1,56.

Проблема ПП2.2.

Якщо молекулярна маса дорівнює мільйону г/моль, то log (M _w) = 6. Інтерполяція, журнал ([η]) = 4, або [η] = 10000 мл/г.

Проблема ПП2.3.

Якщо внутрішня в'язкість, [η] = 800 мл/г, то лог ([η]) = 2,9. Інтерполяція, лог (M _w) = 5.1, або M _w = 126 000 г/моль.

Проблема РР2.4.

Етиленгліколь може утворювати водневі зв'язки на будь-якому кінці молекули, утворюючи надмолекулярну збірку, подібну до полімеру. В результаті він має набагато більший опір в розчині, більш високу в'язкість.

Проблема ПП3.1.

Мед являє собою концентрований розчин простих цукрів, які представляють собою дрібні молекули. Патока, хоч і схожа на мед в чомусь, також містить крохмалі, які є полімерами. Цей полімерний вміст призводить до поведінки зсуву.

Проблема ПП4.1.

а) Існує скляний перехід при температурі близько -18° C.

б) Існує температура плавлення близько 125° C.

в) Існує скляний перехід при температурі близько -4° C.

г) Існує скляний перехід при температурі близько 117° C і температура плавлення близько 146° C.

Проблема РП5.1.

а) T _g спостерігається при температурі близько 78° C, T _m спостерігається при температурі близько 117° C, а T _c спостерігається при температурі близько 104° C.

б) T _g спостерігається при температурі близько 134° C, а T _m спостерігається при температурі близько 167° C, але T _c не спостерігається; зразок не встиг кристалізуватися, але залишився аморфним твердим тілом.

в) T _m спостерігається при температурі близько 194° C, а T _c спостерігається при температурі близько 187° C. t _g не спостерігається і, ймовірно, зустрічається нижче 150° C

г) T _g спостерігається при температурі близько 123° C, але T _m не спостерігається. Експеримент перевіряв набагато вище Т _г (понад сто градусів), тому матеріал може бути аморфним твердим тілом.

Проблема ПП6.1.

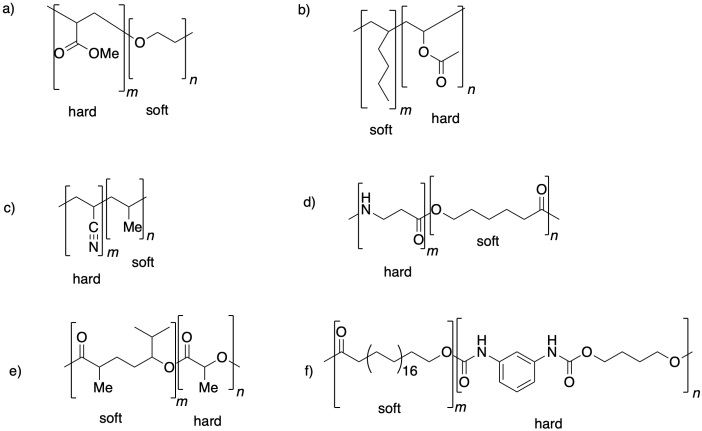
Проблема ПП6.2.

а) д = (2 х 3,14)/0,40 = 16 Å; д = (2 х 3,14)/0,70 = 9,0 Å

б) д = (2 х 3,14)/0,25 = 25 Å; д = (2 х 3,14)/0,85 = 7,4 Å

в) д = (2 х 3,14)/0,25 = 25 Å; д = (2 х 3,14)/0,52 = 12 Å; д = (2 х 3,14)/0,66 = 10 Å

Проблема ПП7.1.

а) гранична міцність на розрив = 800 Па; деформація при розриві = 55%

б) гранична міцність на розрив = 750 Па; деформація при розриві = 215%

в) гранична міцність на розрив = 220 Па; деформація при розриві = 120%

Проблема ПП7.2.

а) Е = σ/ε = 180 Па/0,30 = 600 Па

б) Е = σ/ε = 450 Па/0,15 = 3000 Па

в) Е = σ/ε = 50 Па/0,25 = 200 Па

г) Е = σ/ε = 75 Па/0,30 = 250 Па

Проблема п.7.3.

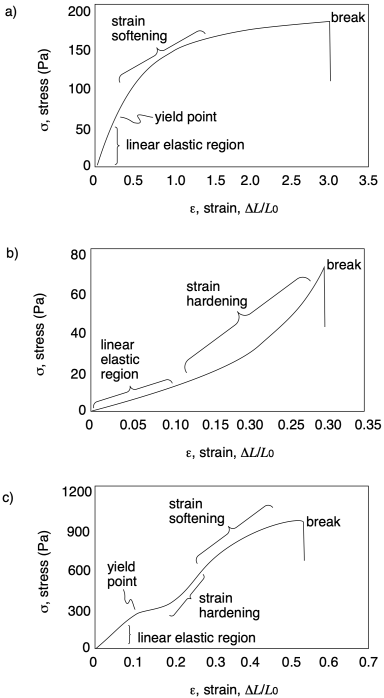
Проблема РП8.1.

1 Па = 1 Па

1 кПа = 1,000 Па

1 МПа = 1 000 000 Па

1 ГПа = 1 000 000 000 Па

Проблема РР9.1.

а) склоподібний: модуль зберігання = 15 МПа; модуль втрат = 70 кПа

гума: модуль зберігання = 7 МПа; модуль втрат = 80 кПа

б) склоподібний: модуль зберігання = 600 кПа; модуль втрат = 140 кПа

гума: модуль зберігання = 130 кПа; модуль втрат = 150 кПа

в) склоподібний: модуль зберігання = 320 кПа; модуль втрат = 80 кПа

гума: модуль зберігання = 70 кПа; модуль втрат = 70 кПа

Проблема РП9.2.

а) 89 °C

б) 170° C

в) 124 °C