16.2: Ентропія

Цілі навчання

• Визначення ентропії
• Поясніть взаємозв'язок між ентропією і кількістю мікростанів
• Прогнозувати ознаку зміни ентропії для хімічних і фізичних процесів

У 1824 році, у віці 28 років, Ніколя Леонард Саді Карно (рис.\(\PageIndex{2}\)) опублікував результати великого дослідження щодо ефективності парових теплових двигунів. У більш пізньому огляді висновків Карно Рудольф Клаузіус представив нову термодинамічну властивість, яка пов'язує спонтанний тепловий потік, що супроводжує процес, з температурою, при якій відбувається процес. Ця нова властивість була виражена як співвідношення оборотного тепла (q _rev) і температури Кельвіна (T). Термін оборотний процес відноситься до процесу, який відбувається з такою повільною швидкістю, що він завжди знаходиться в рівновазі, і його напрямок може бути змінений (його можна «змінити») нескінченно невеликою зміною - це якась умова. Зауважте, що ідея оборотного процесу - це формалізм, необхідний для підтримки розвитку різних термодинамічних концепцій; ніякі реальні процеси не є дійсно оборотними, скоріше вони класифікуються як незворотні.

Малюнок\(\PageIndex{1}\): (а) Дослідження Ніколаса Леонарда Саді Карно в галузі парових машин та (б) Пізніше дослідження Рудольфа Клаузіуса цих висновків призвели до новаторських відкриттів щодо спонтанних процесів теплового потоку.

Подібно до інших термодинамічних властивостей, ця нова величина є функцією стану, і тому її зміна залежить лише від початкового та кінцевого станів системи. У 1865 році Клаузіус назвав цю властивість ентропії (S) і визначив її зміну для будь-якого процесу наступним чином:

\[ΔS=\dfrac{q_\ce{rev}}{T} \label{Eq1} \]

Зміна ентропії для реального, незворотного процесу тоді дорівнює тому, що для теоретичного оборотного процесу, який включає ті ж початкові та кінцеві стани.

Ентропія і мікростани

Після роботи Карно і Клаузіуса Людвіг Больцман розробив молекулярно-масштабну статистичну модель, яка пов'язувала ентропію системи з кількістю мікростанів, можливих для системи. Мікростан (\(\Omega\))це специфічна конфігурація місць розташування та енергій атомів або молекул, які складають таку систему:

\[S=k \ln \Omega \label{Eq2} \]

Тут k - константа Больцмана і має значення\(1.38 \times 10^{−23}\, J/K\).

Що стосується інших функцій стану, то зміна ентропії для процесу - це різниця між його кінцевими (S _f) і початковими (S _i) значеннями:

\[\begin{align} ΔS &=S_\ce{f}−S_\ce{i} \nonumber \\[4pt] &=k \ln \Omega_\ce{f} − k \ln \Omega_\ce{i} \nonumber \\[4pt] &=k \ln\dfrac{\Omega_\ce{f}}{\Omega_\ce{i}} \label{Eq2a} \end{align} \]

Для процесів, пов'язаних зі збільшенням кількості мікростанів системи\(\Omega_f > \Omega_i\), підвищується ентропія системи,\(ΔS > 0\). І навпаки, процеси, що зменшують кількість мікростанів в системі\(\Omega_f < \Omega_i\), дають зниження ентропії системи,\(ΔS < 0\). Ця молекулярно-масштабна інтерпретація ентропії дає посилання на ймовірність того, що процес відбудеться, як показано в наступних параграфах.

Малюнок\(\PageIndex{2}\): Показані шістнадцять мікростанів, пов'язаних з розміщенням чотирьох частинок у двох коробках. Мікростани збираються у п'ять розподілів - (a), (b), (c), (d) та (e) - на основі кількості частинок у кожній коробці.

П'ять рядків діаграм, схожих на доміно, показані та позначені a, b, c, d та e Рядок a має одне «доміно», яке має чотири точки з лівого боку, червону, зелену, синю та жовту за годинниковою стрілкою у верхній лівій частині та без крапок праворуч. Рядок b має чотири «доміно», кожен з яких має три крапки зліва та одну крапку праворуч. Перший показує «доміно» із зеленим, жовтим і синім зліва та червоним праворуч. Друге «доміно» має жовтий, синій і червоний зліва і зелений справа. Третій «доміно» має червоний, зелений та жовтий зліва та синій праворуч, а четвертий - червоний, зелений та синій зліва та жовтий праворуч. Рядок c має шість «доміно», кожен з яких має дві точки з обох сторін. Перший має червоний і зелений зліва і синьо-жовтий праворуч. Другий має червоний і синій зліва і зелений і жовтий праворуч, а третій - жовтий і червоний зліва і зелений і синій праворуч. Четвертий має зелений і синій зліва і червоний і жовтий справа. П'ятий має зелений і жовтий зліва і червоний і синій праворуч. Шостий має синій і жовтий зліва і зелений і червоний праворуч. Рядок d має чотири «доміно», кожен з яких має одну крапку зліва і три праворуч. Перше «доміно» має червоний зліва і синій, зелений і жовтий справа. Другий має зелений зліва і червоний, жовтий і синій праворуч. Третій має синій зліва і червоний, зелений і жовтий справа. Четвертий має жовтий зліва і червоний, зелений і синій праворуч. Рядок е має 1 «доміно» без крапок ліворуч і чотири точки праворуч, які є червоними, зеленими, синіми та жовтими.

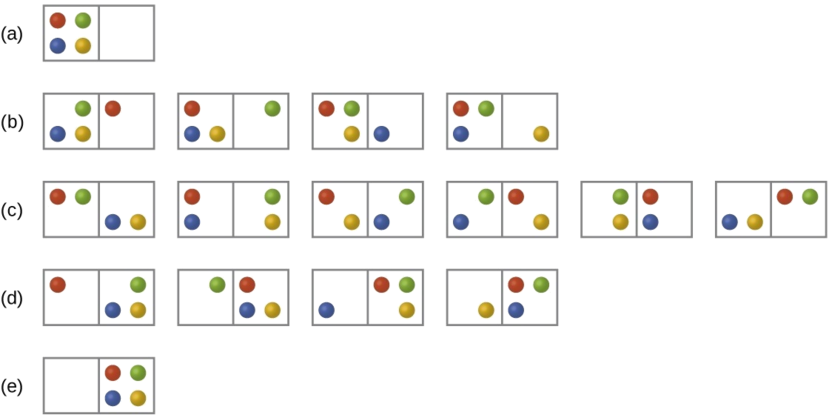
Розглянемо загальний випадок системи, що складається з N частинок, розподілених між n коробками. Кількість мікростанів, можливих для такої системи, дорівнює n ^N. Наприклад, розподіл чотирьох частинок між двома коробками призведе до 2 ⁴ = 16 різних мікростанів, як показано на малюнку\(\PageIndex{2}\). Мікростани з еквівалентними розташуваннями частинок (не враховуючи окремих ідентичностей частинок) групуються разом і називаються розподілами (іноді їх називають макростанами або конфігураціями). Імовірність того, що система буде існувати з її компонентами в заданому розподілі, пропорційна кількості мікростанів у розподілі. Оскільки ентропія зростає логарифмічно з кількістю мікростанів, найбільш ймовірним розподілом є, отже, найбільша ентропія.

Для цієї системи найбільш ймовірною конфігурацією є одне з шести мікростанів, пов'язаних з розподілом (c), де частинки рівномірно розподілені між коробками, тобто конфігурація двох частинок у кожній коробці. Імовірність знаходження системи в даній конфігурації дорівнює

 

\[\dfrac{6}{16} = \dfrac{3}{8} \nonumber \]

Найменш ймовірною конфігурацією системи є така, в якій всі чотири частинки знаходяться в одній коробці, що відповідає розподілам (а) і (е), кожна з ймовірністю

\[\dfrac{1}{16} \nonumber \]

Імовірність знаходження всіх частинок лише в одному полі (лівому або правому полі)

\[\left(\dfrac{1}{16}+\dfrac{1}{16}\right)=\dfrac{2}{16} = \dfrac{1}{8} \nonumber \]

 

У міру додавання більшої кількості частинок в систему кількість можливих мікростанів збільшується експоненціально (2 ^N). Макроскопічна (лабораторного розміру) система, як правило, складається з родимок частинок (N ~ 10 ²³), і відповідна кількість мікростанів буде надзвичайно величезною. Незалежно від кількості частинок в системі, однак, розподіли, в яких приблизно однакова кількість частинок знаходиться в кожній коробці, завжди є найбільш ймовірними конфігураціями.

Таким чином, найбільш імовірним розподілом є найбільша ентропія.

Попередній опис ідеального газу, що розширюється у вакуум, є макроскопічним прикладом цієї моделі частинок в коробці. Для цієї системи найбільш ймовірним розподілом підтверджується той, в якому речовина найбільш рівномірно розсіюється або розподіляється між двома колбами. Спонтанний процес, при якому газ, що міститься спочатку в одній колбі, розширюється, заповнюючи обидві колби однаково, тому дає збільшення ентропії для системи.

Малюнок\(\PageIndex{3}\): На цьому показана модель мікростану, що описує потік тепла від гарячого об'єкта до холодного об'єкта. (a) Перед тим, як відбувається тепловий потік, об'єкт, що складається з частинок A і B, містить обидві одиниці енергії і представлений розподілом трьох мікростанів. (b) Якщо тепловий потік призводить до рівномірного розсіювання енергії (одна енергетична одиниця передається), відбувається розподіл чотирьох мікростанів. (c) Якщо передаються обидві одиниці енергії, отриманий розподіл має три мікростану.

Показано три рядки з позначками a, b та c, кожен з яких містить прямокутники з двома сторонами, де ліва сторона позначена: «A» та «B», а праворуч позначено «C» та «D». Рядок a має три прямокутники, де перший має крапку над і нижче букви A, другий має крапку над A і B, а третій, який має крапку над і нижче букви B. Рядок b має чотири прямокутники; перший має крапку вище A і C, другий має крапку вище A і D, третій має крапку над B і C і четвертий має крапку над B і D. Рядок c має три прямокутники; перший має крапку над і нижче букви C, другий має крапку вище C і D, а третій має крапку над і нижче букви D.

Подібний підхід може бути використаний для опису спонтанного потоку тепла. Розглянемо систему, що складається з двох об'єктів, кожен з яких містить дві частинки, і двох одиниць енергії (представлених як «*») на рис\(\PageIndex{3}\). Гарячий об'єкт складається з частинок A і B і спочатку містить обидві одиниці енергії. Холодний об'єкт складається з частинок C і D, які спочатку не мають енергетичних одиниць. Розподіл (а) показує три мікростану, можливі для початкового стану системи, причому обидві одиниці енергії містяться в гарячому об'єкті. Якщо передається одна з двох одиниць енергії, результатом є розподіл (б), що складається з чотирьох мікростанів. Якщо передаються обидві одиниці енергії, то результатом є розподіл (в), що складається з трьох мікростанів. І так, ми можемо описати цю систему в цілому десятьма мікростанами. Імовірність того, що тепло не тече при контакті двох об'єктів, тобто, що система залишається в розподілі (а), є\(\frac{3}{10}\). Більш імовірно, що потік тепла дає один з двох інших розподілу, сукупна ймовірність бути\(\frac{7}{10}\). Найбільш вірогідним результатом є потік тепла для отримання рівномірного розсіювання енергії, представленої розподілом (b), ймовірність такої конфігурації є\(\frac{4}{10}\). Що стосується попереднього прикладу розгону речовини, екстраполяція цієї обробки на макроскопічні колекції частинок різко збільшує ймовірність рівномірного розподілу щодо інших розподілів. Це підтримує загальне спостереження, що розміщення гарячих і холодних предметів в контакті призводить до спонтанного теплового потоку, який в кінцевому підсумку вирівнює температуру об'єктів. І, знову ж таки, цей спонтанний процес також характеризується підвищенням ентропії системи.

Приклад\(\PageIndex{1}\): Determination of ΔS

Розглянемо наведену тут систему. Яка зміна ентропії для процесу, який перетворює систему з розподілу (a) на (c)?

 

Діаграма показує один прямокутник з двома сторонами, який має чотири точки, червоні, зелені, жовті та сині написані на лівій стороні. Стрілка, спрямована вправо, веде до ще шести двосторонніх прямокутників, кожен з яких має дві точки на лівій і правій стороні. Перший прямокутник має червону та зелену крапку зліва та синьо-жовту праворуч, а другий - червоний та синій ліворуч, а зелений та жовтий праворуч. Третій прямокутник має червону та жовту крапку зліва та синьо-зелену праворуч, а четвертий - зелений та синій ліворуч, а червоно-жовтий - праворуч. П'ятий прямокутник має жовту та зелену крапку зліва та синьо-червону праворуч, а шостий - жовтий та синій зліва та зелений та червоний праворуч.

Рішення

Нас цікавить наступна зміна:

Початкова кількість мікростанів - одне, останні шість:

\[\begin{align} ΔS &=k \ln\dfrac{\Omega_\ce{c}}{\Omega_\ce{a}} \nonumber \\[4pt] &= 1.38×10^{−23}\:J/K × \ln\dfrac{6}{1} \nonumber \\[4pt] &= 2.47×10^{−23}\:J/K \nonumber \end{align} \nonumber \]

Ознака цього результату узгоджується з очікуванням; оскільки мікростанів можливо більше, ніж для початкового стану, зміна ентропії має бути позитивним.

Вправа\(\PageIndex{1}\)

Розглянемо систему, зображену на малюнку\(\PageIndex{3}\). Яка зміна ентропії для процесу, коли вся енергія передається від гарячого об'єкта (АВ) до холодного об'єкта (CD)?

Відповідь

0 ДЖ/К

Прогнозування знака Δ S

Описані раніше взаємозв'язки між ентропією, мікростанами та розсіюванням речовини/енергії дозволяють зробити узагальнення щодо відносних ентропій речовин і прогнозувати ознаку змін ентропії для хімічних і фізичних процесів. Розглянемо фазові зміни, проілюстровані на малюнку\(\PageIndex{4}\). У твердій фазі атоми або молекули обмежені майже фіксованими позиціями відносно один одного і здатні лише скромні коливання щодо цих положень. Маючи по суті фіксовані місця для частинок компонентів системи, кількість мікростанів відносно невелика. У рідкій фазі атоми або молекули можуть вільно переміщатися один від одного і навколо, хоча вони залишаються у відносно безпосередній близькості один від одного. Ця підвищена свобода руху призводить до більшої зміни можливих місць розташування частинок, тому кількість мікростанів відповідно більша, ніж для твердого тіла. В результаті S _рідина > S _тверда речовина і процес перетворення речовини з твердого в рідке (плавлення) характеризується збільшенням ентропії, Δ S > 0. За тією ж логікою зворотний процес (заморожування) проявляє зниження ентропії, Δ S < 0.

Малюнок\(\PageIndex{4}\): Ентропія речовини збільшується (ΔS > 0), коли вона перетворюється з відносно впорядкованої твердої речовини в менш впорядковану рідину, а потім до ще менш впорядкованого газу. Ентропія зменшується (ΔS < 0), коли речовина перетворюється з газу в рідину, а потім у тверду речовину.

Три закриті колби показані зі стрілками вправо та вліво між ними; перша позначена вище як «дельта S більше 0», а нижче як «дельта S менше 0», тоді як друга позначена вище як «дельта S більше 0», а нижче як «дельта S менше 0». Довга, спрямована вправо стрілка намальована над усіма колбами і позначена «Збільшення ентропії». Ліва колба містить двадцять сім частинок, розташованих в кубі в нижній частині колби і позначена нижче «Кристалічне тверде тіло». Середня колба містить двадцять сім частинок, диспергованих випадковим чином на дні колби і позначена нижче «Рідина». Права колба містить двадцять сім частинок, диспергованих всередині колби і швидко рухаються і має маркування «Газ» нижче.

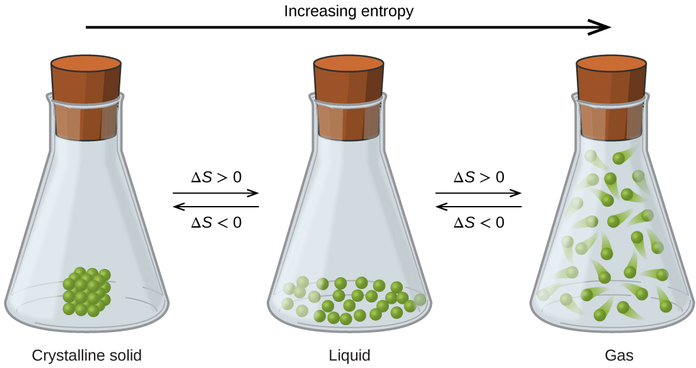
Тепер розглянемо парову або газову фазу. Атоми або молекули займають набагато більший об'єм, ніж у рідкій фазі; тому кожен атом або молекулу можна знайти в набагато більшій кількості місць, ніж у рідкій (або твердій) фазі. Отже, для будь-якої речовини S _газ > S _рідина > S _тверда речовина, і процеси випаровування і сублімації аналогічно передбачають збільшення ентропії, Δ S > 0. Аналогічно, зворотні фазові переходи, конденсація та осадження, включають зменшення ентропії, Δ S < 0.

Відповідно до кінетико-молекулярної теорії температура речовини пропорційна середній кінетичній енергії його частинок. Підвищення температури речовини призведе до більш широких коливань частинок у твердих тілах та швидшому переміщенню частинок у рідини та гази. При більш високих температурах розподіл кінетичних енергій між атомами або молекулами речовини також ширше (більш дисперсне), ніж при більш низьких температурах. Таким чином, ентропія для будь-якої речовини зростає з температурою (рис.\(\PageIndex{5}\)).

Малюнок\(\PageIndex{5}\): Ентропія збільшується з підвищенням температури речовини, що відповідає більшому поширенню кінетичних енергій. Коли речовина плавиться або випаровується, воно відчуває значне збільшення ентропії.

Показані два графіки. Вісь Y лівого графіка позначена як «Дракція молекул», а вісь x позначена «Швидкість, v (м/s)» і має значення від 0 до 1500 вздовж осі з кроком 500. На цьому графіку нанесено чотири лінії. Перший, позначений «100 K», досягає піків близько 200 м/с, тоді як другий, позначений «200 К», досягає піків близько 300 м/с і трохи нижче по осі y, ніж перший. Третя лінія, позначена «500 К», досягає позначки близько 550 м/с і нижче перших двох на осі Y. Четверта лінія, позначена «1000 К», досягає піку близько 750 м/с і є найнижчою з чотирьох на осі y. Кожна лінія стає все більш широкою. Другий графік має вісь y з позначенням «Ентропія, S» зі стрілкою вгору та віссю x з позначкою «Температура (K)» та стрілкою вправо. Графік має три однаково розташовані стовпці на задньому плані, позначені: «Тверда», «Рідина» та «Газ» зліва направо. Лінія простягається трохи вгору через перший стовп в невеликому напрямку вгору, потім йде прямо вгору в переході між першими двома стовпчиками. Потім просувається в невеликому напрямку вгору через другу колону, потім різко йде вгору між другим і третім колонами, потім продовжується в невеликому напрямку вгору ще раз. Перша вертикальна область цієї лінії позначена «Плавлення», а друга - «Кипіння».

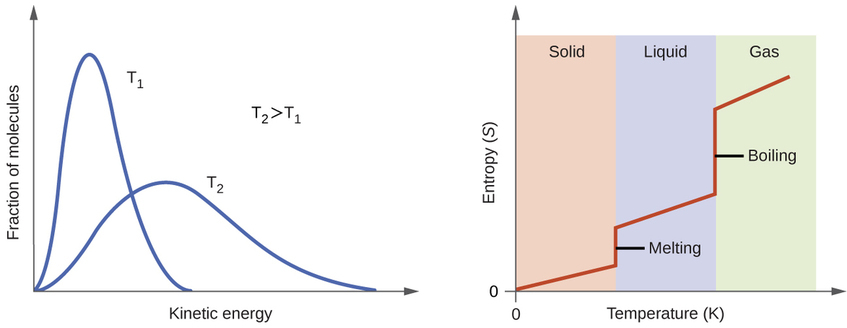
На ентропію речовини впливає структура частинок (атомів або молекул), що входять до складу речовини. Що стосується атомних речовин, то важчі атоми мають більшу ентропію при заданій температурі, ніж легші атоми, що є наслідком зв'язку між масою частинки та інтервалом квантованих рівнів поступальної енергії (що є темою поза межами нашого лікування). Для молекул більша кількість атомів (незалежно від їх маси) збільшує способи, за допомогою яких молекули можуть вібрувати, і, отже, кількість можливих мікростанів та ентропії системи.

Нарешті, варіації типів частинок впливають на ентропію системи. У порівнянні з чистою речовиною, в якому всі частинки ідентичні, ентропія суміші двох і більше різних типів частинок більше. Це пов'язано з додатковими орієнтаціями та взаємодіями, які можливі в системі, що складається з неідентичних компонентів. Наприклад, коли тверда речовина розчиняється в рідині, частинки твердого речовини відчувають як більшу свободу руху, так і додаткові взаємодії з частинками розчинника. Це відповідає більш рівномірному розгону речовини і енергії і більшій кількості мікростанів. Таким чином, процес розчинення включає збільшення ентропії, Δ S > 0.

Враховуючи різні фактори, що впливають на ентропію, ми можемо робити обґрунтовані прогнози знака Δ S для різних хімічних та фізичних процесів, як показано на прикладі.

Приклад\(\PageIndex{2}\): Predicting the Sign of ∆S

Прогнозують ознаку зміни ентропії для наступних процесів. Вкажіть причину кожного з ваших прогнозів.

1. Один моль рідкої води кімнатної температури,\(⟶\) один моль, рідка вода при 50 °С.
2. \(\ce{Ag+}(aq)+\ce{Cl-}(aq)⟶\ce{AgCl}(s)\)
3. \(\ce{C6H6}(l)+\dfrac{15}{2}\ce{O2}(g)⟶\ce{6CO2}(g)+\ce{3H2O}(l)\)
4. \(\ce{NH3}(s)⟶\ce{NH3}(l)\)

S рішення

1. позитивний, підвищується температура
2. негативні, зменшення кількості іонів (частинок) в розчині, зниження розсіювання речовини
3. негативне, чисте зменшення кількості газоподібних видів
4. позитивний, фазовий перехід від твердого до рідкого, чисте збільшення розгону речовини

Вправа\(\PageIndex{2}\)

Прогнозують ознаку зміни ентальпії для наступних процесів. Дайте привід для свого прогнозу.

1. \(\ce{NaNO3}(s)⟶\ce{Na+}(aq)+\ce{NO3-}(aq)\)
2. замерзання рідкої води
3. \(\ce{CO2}(s)⟶\ce{CO2}(g)\)
4. \(\ce{CaCO}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)\)

Відповідь на

Позитивний; Тверда речовина розчиняється, даючи збільшення рухливих іонів у розчині.

Відповідь б

Негативний; Рідина стає більш впорядкованою твердою речовиною.

Відповідь c

Позитивний; Відносно впорядковане тверде тіло стає газом

Відповідь d

Позитивний; Існує чистий видобуток одного моля газу.

Резюме

Ентропія (\(S\)) - це функція стану, яка може бути пов'язана з кількістю мікростанів для системи (кількість способів, якими система може бути організована) та співвідношенням оборотного тепла до температури Кельвіна. Це може трактуватися як міра розгону або розподілу речовини та/або енергії в системі, і це часто описується як представляє «розлад» системи. Для даної речовини\(S_{solid} < S_{liquid} \ll S_{gas}\) в даному фізичному стані при заданій температурі ентропія, як правило, більша для більш важких атомів або більш складних молекул. Ентропія збільшується при нагріванні системи і при утворенні розчинів. Використовуючи ці вказівки, можна достовірно передбачити ознаку зміни ентропії для деяких хімічних реакцій.

Ключові рівняння

• \(ΔS=\dfrac{q_\ce{rev}}{T}\)
• S = к пн Ш
• \(ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}\)

Глосарій

ентропія (S)

функція стану, яка є мірою речовини та/або розсіювання енергії всередині системи, визначається кількістю мікростанів системи, часто описується як міра розладу системи

мікростан (Вт)

можлива конфігурація або розташування речовини та енергії всередині системи

оборотний процес

процес, який відбувається так повільно, щоб бути здатним змінити напрямок у відповідь на нескінченно малу зміну умов; гіпотетична конструкція, яка може бути наближена лише реальними процесами, видаленими