12.5: Теорія зіткнень

Last updated
Save as PDF

Page ID: 22580

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Використовуйте постулати теорії зіткнень, щоб пояснити вплив фізичного стану, температури та концентрації на швидкість реакції
Визначте поняття енергії активації та перехідного стану
Використовуйте рівняння Арреніуса в розрахунках, що стосуються констант швидкості з температурою

Ми не повинні дивуватися тому, що атоми, молекули або іони повинні зіткнутися, перш ніж вони зможуть реагувати один з одним. Атоми повинні бути близько один до одного, щоб утворити хімічні зв'язки. Ця проста передумова є основою для дуже потужної теорії, яка пояснює багато спостережень щодо хімічної кінетики, включаючи фактори, що впливають на швидкість реакції. Теорія зіткнень заснована на наступних постулатах:

Постулати теорії зіткнень

Швидкість реакції пропорційна швидкості зіткнень реагентів:\[\mathrm{reaction\: rate ∝ \dfrac{\#\,collisions}{time}} \nonumber \]
Реагуючі види повинні зіткнутися в орієнтації, яка дозволяє контактувати між атомами, які будуть пов'язані між собою у продукті.
Зіткнення повинно відбуватися з достатньою енергією, щоб дозволити взаємне проникнення валентних оболонок реагуючих видів, щоб електрони могли переставляти та утворювати нові зв'язки (і нові хімічні види).

Ми можемо побачити важливість двох фізичних факторів, зазначених у постулатах 2 і 3, орієнтації та енергії зіткнень, якщо розглядати реакцію чадного газу з киснем:

\[\ce{2CO}(g)+\ce{O2}(g)⟶\ce{2CO2}(g) \nonumber \]

Окис вуглецю - забруднююча речовина, що утворюється при спалюванні вуглеводневого палива. Щоб зменшити цей забруднювач, автомобілі мають каталітичні нейтралізатори, які використовують каталізатор для проведення цієї реакції. Це також побічна реакція згоряння пороху, що призводить до спалаху дула для багатьох вогнепальної зброї. Якщо чадний газ і кисень присутні в достатній кількості, реакція спонтанна при високій температурі і тиску.

Першим кроком газофазної реакції між чадним газом і киснем є зіткнення двох молекул:

\[\ce{CO}(g)+\ce{O2}(g)⟶\ce{CO2}(g)+\ce{O}(g) \nonumber \]

Хоча існує багато різних можливих орієнтацій, які дві молекули можуть мати відносно один одного, розглянемо дві представлені на малюнку\(\PageIndex{1}\). У першому випадку киснева сторона молекули чадного газу стикається з молекулою кисню. У другому випадку вуглецева сторона молекули чадного газу стикається з молекулою кисню. Другий випадок явно частіше призводить до утворення вуглекислого газу, який має центральний атом вуглецю, пов'язаний з двома атомами кисню\(\ce{(O=C=O)}\). Це досить простий приклад того, наскільки важлива орієнтація зіткнення в плані створення потрібного продукту реакції.

альт — Малюнок\(\PageIndex{1}\): Ілюстровані два зіткнення, які можуть мати місце між чадним газом і молекулами кисню. Орієнтація стикаються молекул частково визначає, чи відбудеться реакція між двома молекулами.

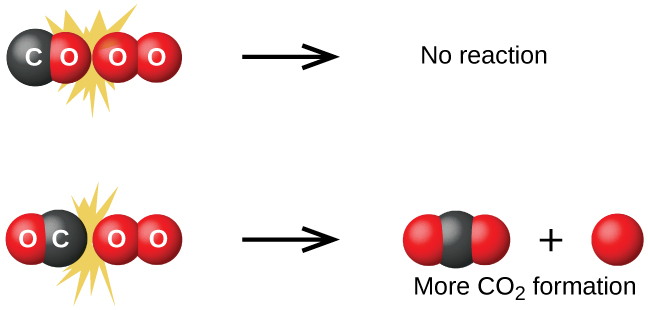
Якщо зіткнення все-таки відбудеться при правильній орієнтації, все одно немає гарантії, що реакція продовжиться з утворенням вуглекислого газу. Кожна реакція вимагає певної кількості енергії активації, щоб вона протікала в прямому напрямку, отримуючи відповідний активований комплекс на цьому шляху. Як\(\PageIndex{2}\) показує малюнок, навіть зіткнення з правильною орієнтацією може не сформувати продукт реакції. При вивченні механізмів реакції кожне з цих трьох розташування атомів називається запропонованим активованим комплексним або перехідним станом.

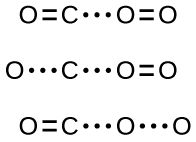
У більшості обставин неможливо виділити або виявити перехідний стан або активований комплекс. У реакції між чадним газом і киснем з утворенням вуглекислого газу активовані комплекси спостерігалися лише спектроскопічно в системах, які використовують гетерогенний каталізатор. Газофазова реакція відбувається занадто швидко, щоб виділити будь-яке подібне хімічна сполука.

Теорія зіткнень пояснює, чому більшість швидкостей реакції збільшуються зі збільшенням концентрацій. Зі збільшенням концентрації будь-якого реагуючого речовини шанси на зіткнення між молекулами збільшуються, оскільки молекул на одиницю об'єму більше. Більше зіткнень означає більш швидку швидкість реакції, припускаючи, що енергія зіткнень адекватна.

Енергія активації та рівняння Арренія

Мінімальна енергія, необхідна для формування продукту при зіткненні між реагентами, називається енергією активації y (\(E_a\)). Кінетична енергія молекул реагентів відіграє важливу роль у реакції, оскільки енергія, необхідна для формування продукту, забезпечується зіткненням молекули реагенту з іншою молекулою реагенту. (В однореактивних реакціях енергія активації може забезпечуватися зіткненням молекули реагенту зі стінкою реакційної судини або з молекулами інертного забруднювача.) Якщо енергія активації набагато більша за середню кінетичну енергію молекул, реакція буде відбуватися повільно: лише кілька швидко рухаються молекул матимуть достатньо енергії, щоб реагувати. Якщо енергія активації набагато менша за середню кінетичну енергію молекул, частка молекул, що володіють необхідною кінетичною енергією, буде великою; більшість зіткнень між молекулами призведе до реакції, і реакція буде відбуватися швидко.

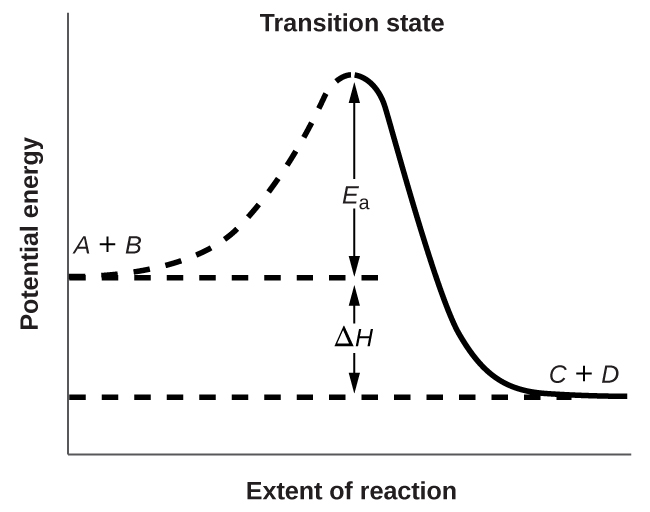
\(\PageIndex{3}\)На малюнку показані енергетичні зв'язки для загальної реакції молекули\(A\) з молекулою з\(B\) утворенням молекул\(C\) і\(D\):

\[A+B⟶C+D \nonumber \]

На малюнку видно, що енергія перехідного стану вище, ніж у реагентів\(A\) і\(B\) на величину, рівну\(E_a\), енергії активації. Таким чином, сума кінетичних енергій\(A\) і\(B\) повинна бути дорівнює або більше Е _а для досягнення перехідного стану. Після того, як перехідний стан досягнуто, і як\(C\) і\(D\) починає формуватися, система втрачає енергію до тих пір, поки її загальна енергія не виявиться нижчою, ніж у вихідної суміші. Ця втрачена енергія передається іншим молекулам, даючи їм достатньо енергії для досягнення перехідного стану. Тому пряма реакція (що між молекулами\(A\) і\(B\)) має тенденцію протікати легко, як тільки реакція почалася. На\(\PageIndex{3}\) малюнку\(ΔH\) представлена різниця в ентальпії між реагентами (\(A\)і\(B\)) і продуктами (\(C\)і\(D\)). Сума\(E_a\) і\(ΔH\) являє собою енергію активації для зворотної реакції:

\[C+D⟶A+B \nonumber \]

Ми можемо використовувати рівняння Арренія, щоб зв'язати енергію активації та постійну швидкості, k, заданої реакції:

\[k=Ae^{−E_a/RT} \label{Arrhenius} \]

У цьому рівнянні

\(R\)ідеальна газова константа, яка має значення 8,314 Дж/моль/К,
\(T\)це температура за шкалою Кельвіна,
\(E_a\)енергія активації в джоулі на моль,
\(e\)є постійною 2.7183, і
\(A\)це константа, яка називається частотним фактором, яка пов'язана з частотою зіткнень і орієнтацією реагуючих молекул.

Обидва постулати теорії зіткнення швидкостей реакції розміщені в рівнянні Арренія. Коефіцієнт частоти А пов'язаний зі швидкістю, з якою відбуваються зіткнення, що мають правильну орієнтацію. Експоненціальний термін пов'язаний з часткою зіткнень\(e^{−E_a/RT}\), що забезпечують адекватну енергію для подолання бар'єру активації реакції.

В одній крайності система не містить достатньо енергії для зіткнень для подолання бар'єру активації. У таких випадках ніякої реакції не відбувається. З іншого боку, система має стільки енергії, що кожне зіткнення з правильною орієнтацією може подолати бар'єр активації, змушуючи реакцію протікати. У таких випадках реакція протікає практично миттєво.

Рівняння Арренія (Equation\ ref {Arrhenius}) описує кількісно більшу частину того, що ми вже обговорювали про швидкість реакції. Для двох реакцій при однаковій температурі реакція з більшою енергією активації має меншу постійну швидкість і повільнішу швидкість. Більша величина\(E_a\) призводить до меншого значення для\(e^{−E_a/RT}\), що відображає меншу частку молекул з достатньою енергією для реакції. Як варіант, реакція з меншими\(E_a\) має більшу частку молекул з достатньою енергією для реакції. Це буде відображено як більша величина\(e^{−E_a/RT}\), більша постійна швидкість, і більш швидка швидкість реакції.

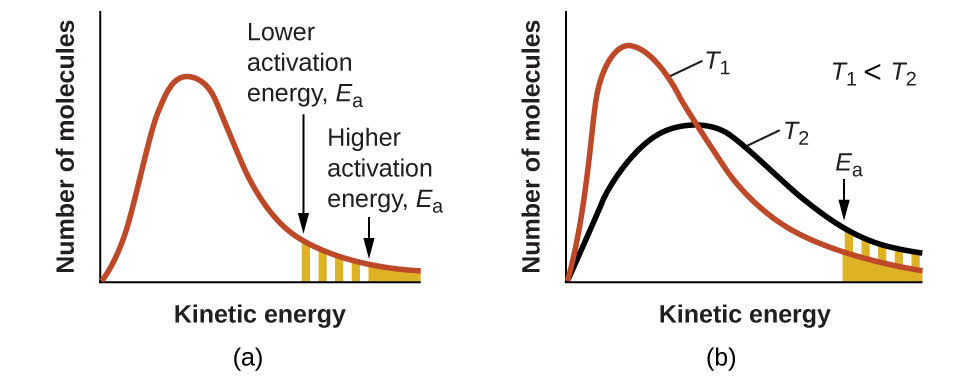
Малюнок\(\PageIndex{4}\): (а) Коли енергія активації реакції зменшується, кількість молекул з принаймні такою великою енергією збільшується, як показано затіненими ділянками. (b) При більш високій температурі Т2 більше молекул мають кінетичні енергії більше, ніж Ea, як показано жовтою затіненою областю.

Підвищення температури має такий же ефект, як і зниження енергії активації. Більша частка молекул має необхідну енергію для реакції (рис.\(\PageIndex{4}\)), про що свідчить збільшення значення\(e^{−E_a/RT}\). Постійна швидкості також прямо пропорційна коефіцієнту частоти,\(A\). Звідси зміна умов або реагентів, що збільшує кількість зіткнень зі сприятливою орієнтацією для реакції, призводить до збільшення\(A\) і, отже, збільшення\(k\).

Зручний підхід до визначення\(E_a\) для реакції передбачає вимірювання\(k\) при різних температурах і використання альтернативного варіанту рівняння Арренія, що приймає форму лінійного рівняння:

\ [\ почати {вирівнювати*}
\ ln k&=\ лівий (\ dfrac {−e_a} {R}\ праворуч)\ лівий (\ dfrac {1} {T}\ праворуч) +\ ln A\\
y&=mx+b
\ end {align*}\ nonumber\]

Таким чином, ділянка\(\ln k\) проти\(\dfrac{1}{T}\) дає пряму лінію з ухилом\(\dfrac{-E_\ce{a}}{R}\), з якого Е _а може бути визначена. Перехоплення дає значення\(\ln A\). Це іноді називають Arrhenius Plot.

Приклад\(\PageIndex{1}\)

Визначення Е _а Тут наведено варіацію константи швидкості з температурою для розкладання HI (g) до H ₂ _{(g) і I 2} (g). Яка енергія активації для реакції?

\[\ce{2HI}(g)⟶\ce{H2}(g)+\ce{I2}(g) \nonumber \]

зміна константи швидкості з температурою для розкладання HI (g) до H2 (g) і I2 (g)
Т (К)	k (л/моль/с)
555	3,52 × 10 ⁻⁷
575	1,22 × 10 ⁻⁶
645	8,59 × 10 ⁻⁵
700	1,16 × 10 ⁻³
781	3,95 × 10 ⁻²

Рішення

Значення\(\dfrac{1}{T}\) і ln k є:

Рішення до прикладу 12.5.1
\(\mathrm{\dfrac{1}{T}\:(K^{−1})}\)	пн м
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)» стиль = "вирівнювання тексту: центр; ">1.80 × 10 ⁻³	−14.860
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)» стиль = "вирівнювання тексту: центр; ">1.74 × 10 ⁻³	−13.617
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)» стиль = "вирівнювання тексту: центр; ">1.55 × 10 ⁻³	−9.362
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)» стиль = "вирівнювання тексту: центр; ">1.43 × 10 ⁻³	−6.759
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)» стиль = "вирівнювання тексту: центр; ">1.28 × 10 ⁻³	−3.231

Рисунок\(\PageIndex{5}\) - це графік ln k проти\(\dfrac{1}{T}\). Для визначення нахилу прямої нам знадобляться два значення ln k, які визначаються з прямої при двох значеннях\(\dfrac{1}{T}\) (краще по одному біля кожного кінця прямої). Наприклад, значення ln k визначається з рядка, коли\(\dfrac{1}{T}=1.25×10^{−3}\) дорівнює −2,593; значення, коли\(\dfrac{1}{T}=1.78×10^{−3}\) дорівнює −14,447.

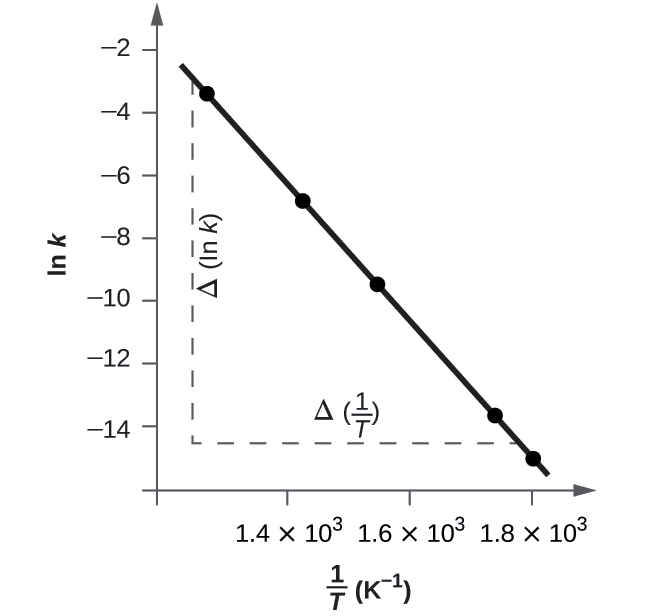
Нахил цієї лінії задається наступним виразом:

\ [\ почати {вирівнювати*}
\ ce {нахил} &=\ dfrac {Δ (\ ln k)} {Δ\ ліворуч (\ dfrac {1} {T}\ праворуч)}\\
&=\ mathrm {\ dfrac {(−14.447) − (−2.593)} {(1.78×10^ {-3}\ :K^ {−1}) − (1.25×10^ {−3}\ :K^ {−1})}}\\
&=\ матхрм {\ dfrac {−11.854} {0.53×10^ {−3}\ :K^ {−1}} =2,2×10^4\ :K}\\
&=−\ dfrac {E_\ ce {a}} {R}
\ кінець {align*}\ nonumber\]

Таким чином:

\[ \begin{align*} E_\ce{a} &=\mathrm{−slope×\mathit R=−(−2.2×10^4\:K×8.314\: J\: mol^{−1}\:K^{−1})} \\[4pt] &=\mathrm{1.8×10^5\:J\: mol^{−1}} \end{align*} \nonumber \]

У багатьох ситуаціях можна отримати розумну оцінку енергії активації, не проходячи весь процес побудови ділянки Арренія. Рівняння Арренія:

\[\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A \nonumber \]

можна переставити, як показано, щоб дати:

\[\dfrac{Δ(\ln k)}{Δ\left(\dfrac{1}{T}\right)}=−\dfrac{E_\ce{a}}{R} \nonumber \]

або

\[\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right) \nonumber \]

Це рівняння можна переставити, щоб дати одноступінчастий розрахунок для отримання оцінки енергії активації:

\[E_\ce{a}=−R\left( \dfrac{\ln k_2−\ln k_1}{\left(\dfrac{1}{T_2}\right)−\left(\dfrac{1}{T_1}\right)}\right ) \nonumber \]

Використовуючи експериментальні дані, представлені тут, ми можемо просто вибрати два записи даних. Для цього прикладу ми вибираємо перший запис і останній запис:

Перший і останній запис
Т (К)	k (л/моль/с)	\(\dfrac{1}{T}\:(K^{-1})\)	пн м
555	3,52 × 10 ⁻⁷	\ (\ dfrac {1} {T}\: (K^ {-1})\)» стиль = "вирівнювання тексту: центр; ">1.80 × 10 ⁻³	−14.860
781	3,95 × 10 ⁻²	\ (\ dfrac {1} {T}\: (K^ {-1})\)» стиль="вирівнювання тексту: центр; ">1.28 × 10 ⁻³	−3.231

Після обчислення\(\dfrac{1}{T}\) і ln k ми можемо підставити в рівняння:

\[E_\ce{a}=\mathrm{−8.314\:J\:mol^{−1}\:K^{−1}\left(\dfrac{−3.231−(−14.860)}{1.28×10^{−3}\:K^{−1}−1.80×10^{−3}\:K^{−1}}\right)} \nonumber \]

_{і результат Е а = 185 900 Дж/моль.}

Цей метод дуже ефективний, особливо коли для цікавить реакції доступна обмежена кількість залежних від температури констант швидкості.

Вправа\(\PageIndex{1}\)

Постійна швидкості розкладання N ₂ O ₅ до NO і O ₂ в газовій фазі становить 1,66 л/моль/с при 650 К і 7,39 л/моль/с при 700 К:

\[\ce{2N2O5}(g)⟶\ce{4NO}(g)+\ce{3O2}(g) \nonumber \]

Припускаючи, що кінетика цієї реакції узгоджується з рівнянням Арренія, обчисліть енергію активації для цього розкладання.

Відповідь: 113 000 Дж/моль

Резюме

Хімічні реакції вимагають зіткнень між видами реагентів. Ці зіткнення реагентів повинні мати належну орієнтацію та достатню енергію, щоб призвести до утворення продукту. Теорія зіткнень дає просте, але ефективне пояснення впливу багатьох експериментальних параметрів на швидкість реакції. Рівняння Арренія описує зв'язок між константою швидкості реакції та енергією її активації, температурою та залежністю від орієнтації зіткнення.

Ключові рівняння

\(k=Ae^{−E_a/RT}\)
\(\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A\)
\(\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right)\)

Глосарій

активований комплекс: (також, перехідний стан) нестабільна комбінація видів реагентів, що представляють найвищий енергетичний стан реакційної системи

енергія активації (Е _а): енергія, необхідна для того, щоб відбулася реакція

Рівняння Арренія: математична залежність між постійною швидкості та енергією активації реакції

теорія зіткнення: модель, яка підкреслює енергію та орієнтацію молекулярних зіткнень для пояснення та прогнозування кінетики реакції

коефіцієнт частоти (А): константа пропорційності в рівнянні Арренія, пов'язана з відносною кількістю зіткнень, що мають орієнтацію, здатну привести до формування продукту