12.4: Закони про інтегровані ставки
- Page ID
- 22563
- Поясніть форму і функції інтегрованого нормового закону
- Виконання інтегрованих розрахунків закону швидкості для реакцій нуль-, першого та другого порядку
- Визначте період напіврозпаду і проведіть відповідні розрахунки
- Визначте порядок реакції на основі даних концентрації/часу
Закони швидкості, які ми бачили до цього часу, стосуються швидкості та концентрації реагентів. Ми також можемо визначити другу форму кожного закону норми, яка пов'язує концентрації реагентів і час. Вони називаються інтегрованими нормовими законами. Ми можемо використовувати інтегрований закон швидкості для визначення кількості реагенту або продукту, присутнього через певний проміжок часу, або для оцінки часу, необхідного для того, щоб реакція протікала певною мірою. Наприклад, інтегрований закон ставки використовується для визначення тривалості часу зберігання радіоактивного матеріалу, щоб його радіоактивність розпалася до безпечного рівня.
Використовуючи обчислення, закон диференціальної швидкості для хімічної реакції може бути інтегрований щодо часу, щоб дати рівняння, яке пов'язує кількість реагенту або продукту, присутнього в реакційній суміші, з минулим часом реакції. Цей процес може бути як дуже простим, так і дуже складним, залежно від складності закону диференціальної ставки. Для обговорення ми зосередимося на результуючих інтегрованих законів ставок для реакцій першого, другого та нульового порядку.
Реакції першого порядку
Рівняння, що стосується постійної швидкості\(k\) до початкової концентрації\([A]_0\) та концентрації,\([A]_t\) присутньої через будь-який заданий час,\(t\) може бути виведено для реакції першого порядку і показано як:
\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber \]
або альтернативно
\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber \]
або
\[[A]=[A]_0e^{−kt} \nonumber \]
Константа швидкості розкладання циклобутану першого порядку\(\ce{C4H8}\) при 500 °С становить 9,2 × 10 −3 с −1:
\[\ce{C4H8⟶2C2H4} \nonumber \]
Скільки часу знадобиться для розкладання 80.0% зразка C 4 H 8?
Рішення
Ми використовуємо інтегровану форму закону про ставки, щоб відповісти на питання щодо часу:
\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber \]
Є чотири змінні в закон ставки, так що якщо ми знаємо три з них, ми можемо визначити четвертий. У цьому випадку ми знаємо [A] 0, [A], і k, і потрібно знайти t.
Початкова концентрація C 4 H 8, [A] 0, не передбачена, але положення про те, що 80.0% зразка розклалося, є достатньою інформацією для вирішення цієї проблеми. Нехай х - початкова концентрація, в цьому випадку концентрація після 80,0% розкладання становить 20,0% х або 0,200 х. перестановка закону норми для виділення t і заміщення наданих величин дає:
\ [\ почати {вирівнювати*}
t&=\ ln\ dfrac {[x]} {[0.200x]} ×\ dfrac {1} {k}\ [4pt]
&=\ mathrm {\ ln\ dfrac {0.100\ :моль\: L^ {−1}} {0,020\ :моль\: L^ {−1}} ×\ dfrac {1} {9.2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ математика {1.609×\ dfrac {1} {9.2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ матрм {1,7 × 10^ 2\ :s}
\ end {align*}\ nonumber\]
Йод-131 - радіоактивний ізотоп, який використовується для діагностики та лікування деяких форм раку щитовидної залози. Йод-131 розпадається до ксенон-131 відповідно до рівняння:
\[\textrm{I-131 ⟶ Xe-131 + electron} \nonumber \]
Розпад першого порядку з константою швидкості 0,138 d −1. Весь радіоактивний розпад - це перший порядок. Скільки днів знадобиться для розпаду 90% йоду−131 у 0,500 М розчині цієї речовини до Xe-131?
- Відповідь
-
16.7 днів
Ми можемо використовувати інтегровані закони швидкості з експериментальними даними, які складаються з інформації про час і концентрацію, щоб визначити порядок і константу швидкості реакції. Інтегрований закон швидкості може бути перебудований у стандартний формат лінійного рівняння:
\ [\ begin {вирівнювання}
\ ln [A] & =( −k) (t) +\ ln [A] _0\ мітка {in1st}\\ [4pt]
y&=mx+b
\ end {вирівнювання}\ nonumber\]
Сюжет\(\ln[A]\) проти\(t\) для реакції першого порядку являє собою пряму лінію з нахилом\(−k\) і перехопленням\(\ln[A]_0\). Якщо набір даних швидкості побудовані таким чином, але не призводять до прямої лінії, реакція не перший порядок\(A\).
Покажіть, що дані на цьому малюнку можуть бути представлені законом швидкості першого порядку шляхом графіків ln [H 2 O 2] проти часу. Визначте постійну швидкості для швидкості розкладання Н 2 О 2 з цих даних.
Рішення
Дані з цього малюнка з додаванням значень ln [H 2 O 2] наведені на рис\(\PageIndex{1}\).
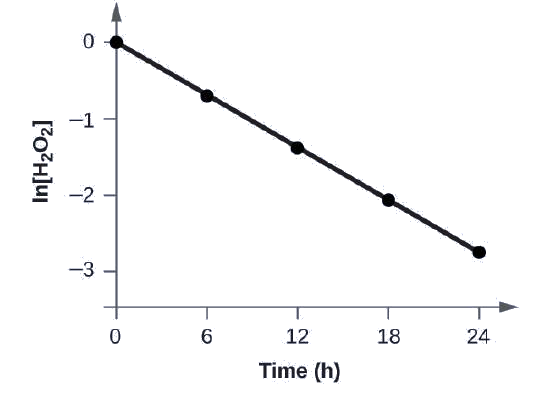
| Пробна версія | Час (ч) | [Н 2 О 2] (М) | лн [Н 2 О 2] |
|---|---|---|---|
| 1 | 0 | 1.000 | 0.0 |
| 2 | 6.00 | 0,500 | −0.693 |
| 3 | 12.00 | 0,250 | −1,386 |
| 4 | 18.00 | 0,125 | −2.079 |
| 5 | 24.00 | 0.0625 | −2.772 |
Графік ln [H 2 O 2] проти часу є лінійним, тому ми перевірили, що реакція може бути описана законом швидкості першого порядку.
Константа швидкості для реакції першого порядку дорівнює негативному нахилу ділянки ln [H 2 O 2] проти часу, коли:
\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber \]
Для того щоб визначити нахил лінії, нам знадобляться два значення ln [H 2 O 2] при різних значеннях t (краще по одному біля кожного кінця лінії). Наприклад, значення ln [H 2 O 2], коли t дорівнює 6,00 h, дорівнює −0,693; значення, коли t = 12,00 h, дорівнює −1,386:
\ [\ почати {вирівнювати*}
\ ce {нахил} &=\ математика {\ dfrac {−1.386− (−0.693)} {12.00\: h−6.00\: h}}\ [4pt]
&=\ математика {\ dfrac {−0.693} {6.00\: h}}\\ [4pt]
&=\ математика {−1.155 × 10^ {−2}\ :h^ {−1}}\\ [4pt]
k&=\ матхрм {−нахил = − (−1,155 × 10^ {−1}\ :h^ {−1}) =1,155 × 10^ {−1}\ :h^ {−1} }
\ end {вирівнювати*}\ nonumber\]
Графік наступних даних, щоб визначити, чи\(A⟶B+C\) є реакція першого порядку.
| Пробна версія | Час (и) | [A] |
|---|---|---|
| 1 | 4.0 | 0,220 |
| 2 | 8.0 | 0.144 |
| 3 | 12.0 | 0.110 |
| 4 | 16.0 | 0,088 |
| 5 | 20.0 | 0.074 |
- Відповідь
-
Ділянка ln [A] vs. t не є прямою лінією. Рівняння не першого порядку:
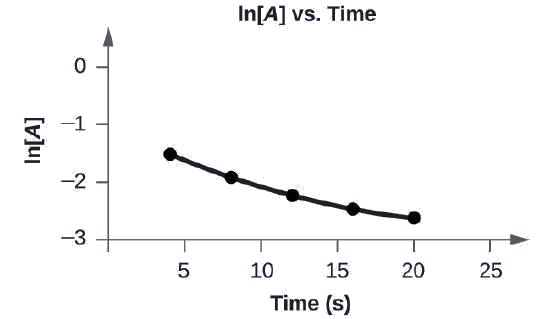
Буде показано графік, позначений вище як «l n [A] vs Time». Вісь x позначено «Час (s)», а вісь y позначена «l n [A]». Вісь X показує маркування на 5, 10, 15, 20 і 25 годин. Вісь Y показує позначки на негативних 3, негативних 2, негативних 1 і 0. Проводиться невелика крива, що з'єднує п'ять точок в координатах приблизно (4, від'ємний 1,5), (8, негативний 2), (12, негативний 2.2), (16, негативний 2.4) і (20, негативний 2.6).
Реакції другого порядку
Рівняння, які пов'язують концентрації реагентів і константу швидкості реакцій другого порядку, досить складні. Обмежимося найпростішими реакціями другого порядку, а саме тими, з показниками, які залежать лише від концентрації одного реагенту і описуються законом диференціальної швидкості:
\[\ce{Rate}=k[A]^2 \nonumber \]
Для цих реакцій другого порядку інтегрованим нормовим законом є:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd} \]
де члени в рівнянні мають свої звичні значення, визначені раніше.
Реакція газу бутадієну (С 4 Н 6) з самим собою виробляє газ С 8 Н 12 наступним чином:
\[\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber \]
Реакція другого порядку з постійною швидкістю, рівною 5,76 × 10 −2 л/моль/хв при певних умовах. Якщо початкова концентрація бутадієну становить 0,200 М, яка концентрація залишається після 10,0 хв?
Рішення
Ми використовуємо інтегровану форму закону про ставки, щоб відповісти на питання, що стосуються часу. Для реакції другого порядку ми маємо:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
Ми знаємо три змінні в цьому рівнянні: [A] 0 = 0,200 моль/л, k = 5,76 × 10 −2 л/моль/хв, і t = 10,0 хв. Тому ми можемо вирішити для [A], четверту змінну:
\ [\ почати {вирівнювати*}
\ dfrac {1} {[A]} &=\ математика {(5.76×10^ {−2}\ :L\: моль^ {−1}\ :min^ {−1}) (10\ :хв) +\ dfrac {1} {0.200\ :mol^ {−1}}}\\ [4pt]
\ dfrac {1} {[A]} &=\ математика {(5.76×10^ {−1}\ :L\: моль^ {−1}) +5.00\ :L\: моль^ {−1}}\\ [4pt]
\ dfrac {1} {[A]} &=\ матрм {5.58\ :L\: моль^ {−1}}\ 4 пт]
[A] &=\ математика {1.79×10^ {−1}\ :моль\: L^ {−1}}
\ кінець {align*}\ number\]
Тому 0,179 моль/л бутадієну залишаються в кінці 10,0 хв порівняно з 0,200 моль/л, який спочатку був присутній.
Якщо початкова концентрація бутадієну становить 0,0200 М, яка концентрація залишається після 20,0 хв?
- Відповідь
-
0,0196 моль/л
Інтегрований закон швидкості для наших реакцій другого порядку має вигляд рівняння прямої:
\ [\ почати {вирівнювати*}
\ dfrac {1} {[A]} &=kt+\ dfrac {1} {[A] _0}\\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
Ділянка\(\dfrac{1}{[A]}\) проти t для реакції другого порядку являє собою пряму лінію з нахилом k і перехопленням\(\dfrac{1}{[A]_0}\). Якщо ділянка не пряма, то реакція не другого порядку.
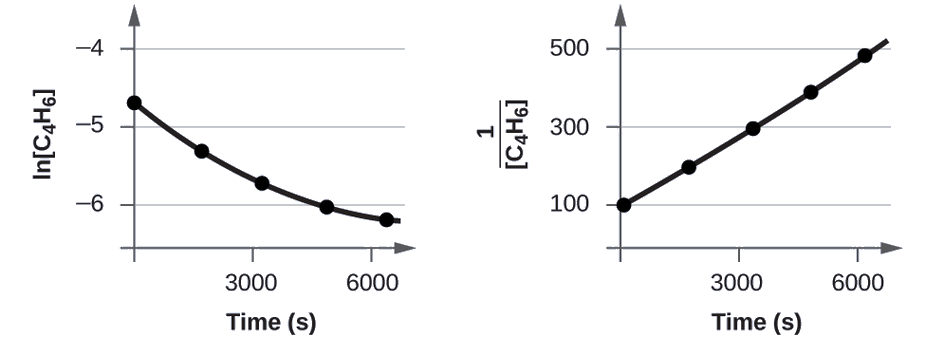
Перевірте дані, щоб показати, чи димеризація C 4 H 6 є реакцією першого або другого порядку.
Рішення
| Пробна версія | Час (и) | [C 4 Ч 6] (М) |
|---|---|---|
| 1 | 0 | 1,00 × 10 −2 |
| 2 | 1600 | 5,04 × 10 −3 |
| 3 | 3200 | 3,37 × 10 −3 |
| 4 | 4800 | 2,53 × 10 −3 |
| 5 | 6200 | 2,08 × 10 −3 |
Для того, щоб відрізнити реакцію першого порядку від реакції другого порядку, ми будуємо ln [C 4 H 6] проти t і порівняємо її з графіком\(\mathrm{\dfrac{1}{[C_4H_6]}}\) проти t. Значення, необхідні для цих ділянок, слідують.
| Час (и) | \(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\) | лн [С 4 Н 6] |
|---|---|---|
| 0 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)» стиль = "вирівнювання тексту: центр; ">100 | −4.605 |
| 1600 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)» стиль = "вирівнювання тексту: центр; ">198 | −5.289 |
| 3200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)» стиль = "вирівнювання тексту: центр; ">296 | −5.692 |
| 4800 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)» стиль ="вирівнювання тексту: центр; ">395 | −5.978 |
| 6200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)» стиль ="вирівнювання тексту: центр; ">481 | −6.175 |
Сюжети наведені на малюнку\(\PageIndex{2}\). Як бачите, сюжет ln [C 4 H 6] проти t не лінійний, тому реакція не першого порядку. Графік\(\dfrac{1}{[\ce{C4H6}]}\) проти t лінійний, що вказує на те, що реакція другого порядку.
Чи відповідають наступні дані закону про ставку другого порядку?
| Пробна версія | Час (и) | [А] (М) |
|---|---|---|
| 1 | 5 | 0,952 |
| 2 | 10 | 0,625 |
| 3 | 15 | 0,465 |
| 4 | 20 | 0,370 |
| 5 | 25 | 0,308 |
| 6 | 35 | 0,230 |
- Відповідь
-
Так. Сюжет\(\dfrac{1}{[A]}\) vs. t лінійний:
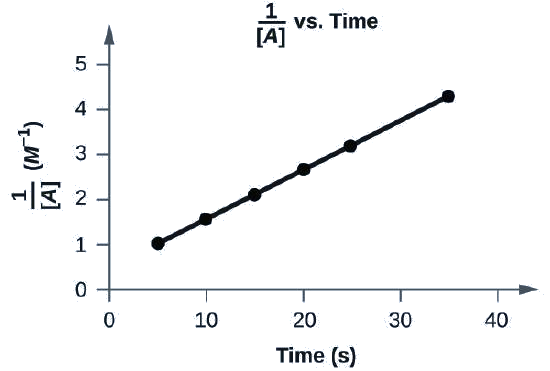
На осі x показано графік із назвою «1, розділений на [A] проти часу», з міткою «Час (и)». Ліворуч від осі y з'являється мітка «1, розділена на [A]». Вісь x показує маркування, що починається з нуля і продовжується з інтервалом від 10 до 40 включно. Вісь Y зліва показує позначки, що починаються з 0 і збільшуються з інтервалами від 1 до 5 включно. Лінія зі зростаючим трендом проводиться через шість точок приблизно (4, 1), (10, 1,5), (15, 2.2), (20, 2,8), (26, 3.4) та (36, 4.4).
Реакції нульового порядку
Для реакцій нульового порядку закон диференціальної швидкості дорівнює:
\[\ce{Rate}=k[A]^0=k \nonumber \]
Таким чином, реакція нульового порядку проявляє постійну швидкість реакції незалежно від концентрації її реагентів.
Інтегрований закон швидкості для реакції нульового порядку також має вигляд рівняння прямої:
\ [\ begin {align*}
[A] &=−kt+ [A] _0\ мітка {intzero}\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
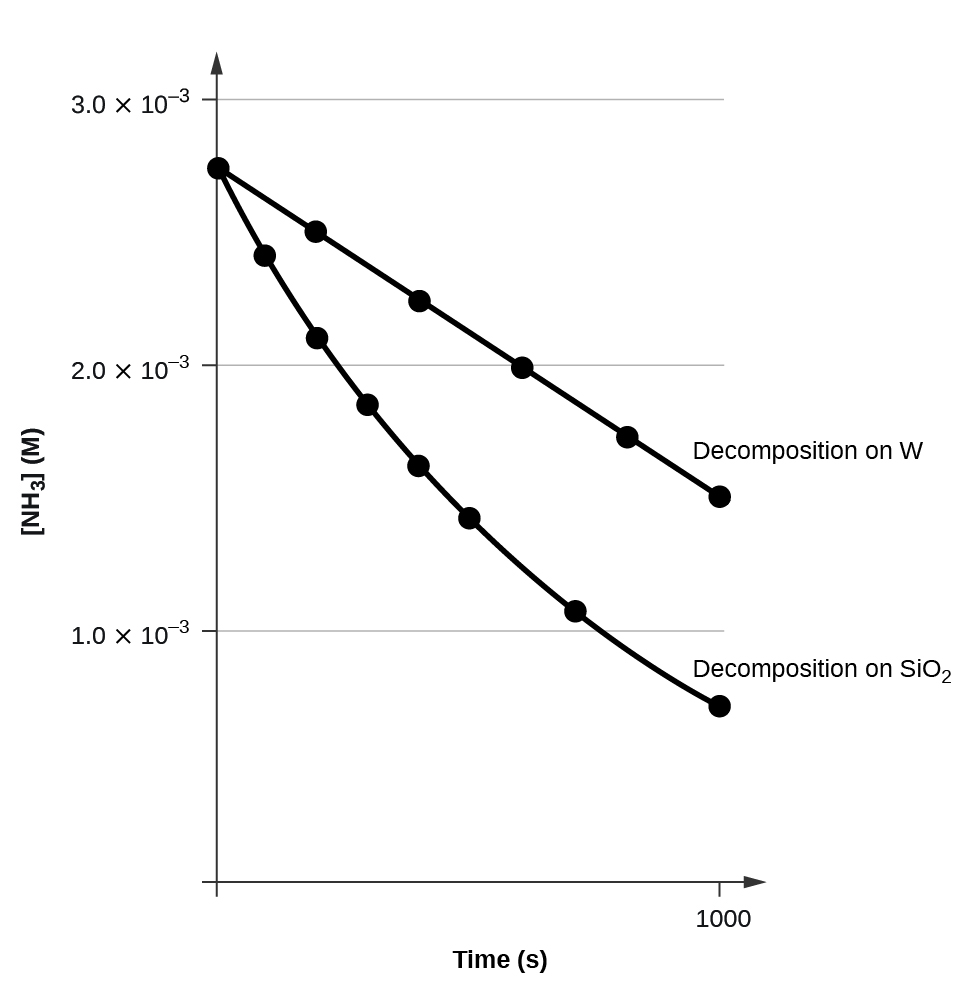
Графік\([A]\) проти\(t\) для реакції нульового порядку є прямою лінією з нахилом −k і перехопленням [A] 0. \(\PageIndex{3}\)На малюнку показаний графік [NH 3] проти t для розкладання аміаку на гарячому вольфрамовому дроті і для розкладання аміаку на гарячому кварці (SiO 2). Розкладання NH 3 на гарячому вольфрамі дорівнює нульовому порядку; ділянка - пряма лінія. Розкладання NH 3 на гарячому кварці не нульовий порядок (це перший порядок). З нахилу лінії для розкладання нульового порядку можна визначити константу швидкості:
\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber \]
Період напіврозпаду реакції
Період напіввиведення реакції (t 1/2) - це час, необхідний для споживання половини заданої кількості реагенту. У кожному наступному період напіврозпаду витрачається половина залишилася концентрації реагенту. На прикладі розкладання перекису водню виявимо, що протягом першого періоду напіввиведення (від 0,00 годин до 6,00 год) концентрація Н 2 О 2 зменшується з 1.000 М до 0.500 М. Протягом другого періоду напіввиведення (з 6.00 годин до 12.00 год) він зменшується з 0,500 М до 0,250 М; протягом третього періоду напіввиведення зменшується з 0,250 М до 0,125 М. Концентрація Н 2 О 2 зменшується вдвічі протягом кожного наступного періоду 6,00 годин. Розпад перекису водню є реакцією першого порядку, і, як можна показати, період напіввиведення реакції першого порядку не залежить від концентрації реагенту. Однак період напіврозпаду реакцій з іншими порядками залежить від концентрації реагентів.
Реакції першого порядку
Ми можемо вивести рівняння для визначення періоду напіврозпаду реакції першого порядку з альтернативної форми інтегрованого закону швидкості наступним чином:
\ [\ почати {вирівнювати*}
\ ln\ dfrac {[A] _0} {[A]} &=kt\\ [4pt]
t&=\ ln\ dfrac {[A] _0} {[A]} ×\ dfrac {1} {k}
\ кінець {вирівнювати*}\ номер\]
Якщо встановити час t рівне періоду напіврозпаду\(t_{1/2}\), то відповідна концентрація А в цей час дорівнює половині його початкової концентрації. Звідси, коли\(t=t_{1/2}\),\([A]=\dfrac{1}{2}[A]_0\).
Тому:
\ [\ почати {вирівнювати*}
t_ {1/2} &=\ ln\ dfrac {[A] _0} {\ dfrac {1} {A] _0} ×\ dfrac {1} {k}\\ [4pt]
&=\ ln 2×\ dfrac {1} {k} {k} =0.693×\ dfrac {1} {k}
кінець {вирівнювати*}\ nonumber\]
Таким чином:
\[t_{1/2}=\dfrac{0.693}{k} \nonumber \]
Ми бачимо, що період напіврозпаду реакції першого порядку обернено пропорційний постійній швидкості k. Швидка реакція (коротший період напіврозпаду) матиме більший k; повільна реакція (довший період напіврозпаду) матиме менший k.
Обчисліть константу швидкості розкладання пероксиду водню першого порядку у воді при 40 °С, використовуючи дані, наведені на рис\(\PageIndex{4}\).
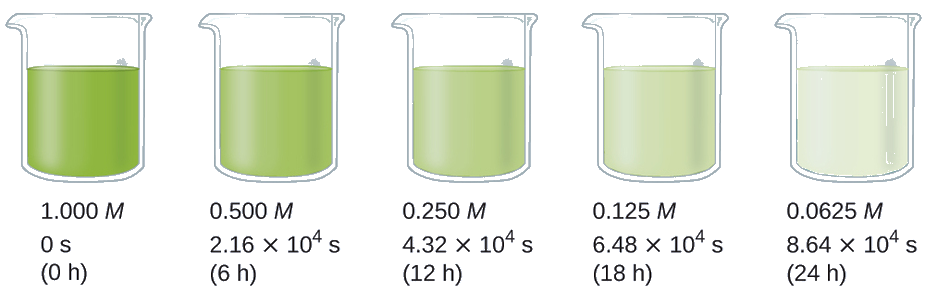
Розчин Період напіввиведення при розкладанні Н 2 О 2 становить 2,16 × 10 4 с:
\ [\ почати {вирівнювати*}
t_ {1/2} &=\ dfrac {0.693} {k}\\ [4pt]
k&=\ dfrac {0.693} {t_ {1/2}} =\ dfrac {0.693} {2.16×10^4\:\ ce s} =3.21×10^ {−5}\:\ ce s^ {−1}
\ end {вирівнювати*}\ nonumber\]
Радіоактивний розпад йоду-131 першого порядку демонструє константу швидкості 0,138 d −1. Який період напіврозпаду для цього розпаду?
- Відповідь
-
5.02 д.
Реакції другого порядку
Ми можемо вивести рівняння для обчислення періоду напіврозпаду другого порядку наступним чином:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
або
\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber \]
Якщо
\[t=t_{1/2} \nonumber \]
потім
\[[A]=\dfrac{1}{2}[A]_0 \nonumber \]
і ми можемо написати:
\ dfrac {1} {\ dfrac {1} {2} [A] _0} −\ dfrac {1} {[A] _0} &=kt_ {1/2}\ [4pt]
2 [A] _0−\ dfrac {1} {[A] _0} &=kt_ {1/2}\ [4pt]
\ dfrac {1} {[A] _0} &=kt_ {1/2}
\ кінець {вирівнювати*}\)
Таким чином:
\[t_{1/2}=\dfrac{1}{k[A]_0} \nonumber \]
Для реакції другого порядку\(t_{1/2}\) обернено пропорційний концентрації реагенту, а період напіввиведення збільшується в міру протікання реакції, оскільки концентрація реагенту зменшується. Отже, ми вважаємо, що використання концепції напіврозпаду є більш складним для реакцій другого порядку, ніж для реакцій першого порядку. На відміну від реакцій першого порядку, константа швидкості реакції другого порядку не може бути розрахована безпосередньо з періоду напіврозпаду, якщо не відома початкова концентрація.
Реакції нульового порядку
Ми можемо вивести рівняння для розрахунку періоду напіврозпаду реакції нульового порядку наступним чином:
\[[A]=−kt+[A]_0 \nonumber \]
Коли половина початкової кількості реагенту була витрачена\(t=t_{1/2}\) і\([A]=\dfrac{[A]_0}{2}\). Таким чином:
\ [\ почати {вирівнювати*}
\ dfrac {[A] _0} {2} &=−kt_ {1/2} + [A] _0\ [4pt]
kt_ {1/2} &=\ dfrac {[A] _0} {2}
\ кінець {align*}\ nonumber\]
і
\[t_{1/2}=\dfrac{[A]_0}{2k} \nonumber \]
Період напіввиведення реакції нульового порядку збільшується зі збільшенням початкової концентрації. Рівняння як для диференціальних, так і інтегральних законів швидкості та відповідних періодів напіврозпаду для реакцій нуль, першого та другого порядку зведені в табл\(\PageIndex{1}\).
| Нульовий порядок | Першого порядку | другого порядку | |
|---|---|---|---|
| ставка закон | швидкість = k | швидкість = k [A] | швидкість = k [A] 2 |
| одиниці постійної швидкості | М с −1 | s −1 | М −1 с −1 |
| інтегрована ставка закон | [A] = − kt + [A] 0 | ln [A] = − kt + на [А] 0 | \(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\) |
| графік, необхідний для лінійного підгонки даних швидкості | [A] проти т | ln [A] проти т | \(\dfrac{1}{[A]}\)проти т |
| зв'язок між нахилом лінійного графіка та постійною швидкості | k = −нахил | k = −нахил | k = +ухил |
| період напіврозпаду | \(t_{1/2}=\dfrac{[A]_0}{2k}\) | \(t_{1/2}=\dfrac{0.693}{k}\) | \(t_{1/2}=\dfrac{1}{[A]_0k}\) |
Резюме
Диференціальні закони ставок можуть визначатися методом початкових ставок або іншими методами. Вимірюється значення початкових швидкостей реакції при різних концентраціях реагентів. З цих вимірів визначаємо порядок реакції в кожному реагенті. Інтегровані закони ставок визначаються шляхом інтеграції відповідних законів диференціальної ставки. Константи швидкості для цих законів швидкості визначаються з вимірювань концентрації в різний час під час реакції.
Період напіввиведення реакції - це час, необхідний для зменшення кількості даного реагенту на половину. Період напіввиведення реакції нульового порядку зменшується, оскільки початкова концентрація реагенту в реакції зменшується. Період напіввиведення реакції першого порядку не залежить від концентрації, і період напіввиведення реакції другого порядку зменшується зі збільшенням концентрації.
Ключові рівняння
- інтегрований закон швидкості для реакцій нульового порядку (Equation\ ref {intzero}):
\([A]=−kt+[A]_0\)з\(t_{1/2}=\dfrac{[A]_0}{2k}\)
- інтегрований закон швидкості для реакцій першого порядку (Equation\ ref {in1st}):
\(\ln[A]=−kt+ \ln[A]_0\)з\(t_{1/2}=\dfrac{0.693}{k}\)
- інтегрований закон швидкості для реакцій другого порядку (Equation\ ref {int2nd}):
\(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\)з\(t_{1/2}=\dfrac{1}{[A]_0k}\)
Глосарій
- період напіввиведення реакції (т л/2)
- час, необхідний для споживання половини заданої кількості реагенту
- інтегрована ставка закон
- рівняння, яке пов'язує концентрацію реагенту з минулим часом реакції
