5.3: Ентальпія

Цілі навчання

• Створити перший закон термодинаміки
• Визначте ентальпію і поясніть її класифікацію як функцію стану
• Написати і збалансувати термохімічні рівняння
• Обчисліть зміни ентальпії для різних хімічних реакцій
• Поясніть закон Гесса і використовуйте його для обчислення ентальпії реакцій

Термохімія - це галузь хімічної термодинаміки, науки, яка займається взаємозв'язками між теплом, роботою та іншими формами енергії в контексті хімічних і фізичних процесів. Оскільки ми зосереджуємося на термохімії в цьому розділі, нам потрібно розглянути деякі широко використовувані поняття термодинаміки.

Речовини виступають в ролі резервуарів енергії, тобто енергію можна додавати до них або видаляти з них. Енергія зберігається в речовині, коли кінетична енергія її атомів або молекул підвищується. Більша кінетична енергія може бути у вигляді збільшених перекладів (подорожі або прямолінійних рухів), вібрацій або обертань атомів або молекул. Коли теплова енергія втрачається, інтенсивність цих рухів зменшується і кінетична енергія падає. Загальна кількість всіх можливих видів енергії, присутніх в речовині, називається внутрішньою енергією (U), іноді символізується як Е.

Оскільки система зазнає змін, її внутрішня енергія може змінюватися, а енергія може передаватися від системи до оточення, або від оточення до системи. Енергія передається в систему, коли вона поглинає тепло (q) з навколишнього середовища або коли оточення працює (w) на системі. Наприклад, енергія передається в металевий дріт кімнатної температури, якщо вона занурена в гарячу воду (провід поглинає тепло від води), або якщо ви швидко згинаєте дріт вперед і назад (провід стає тепліше через виконану на ньому роботи). Обидва процеси збільшують внутрішню енергію проводу, що відбивається на підвищенні температури проводу. І навпаки, енергія передається з системи, коли тепло втрачається від системи, або коли система працює над навколишнім середовищем.

Зв'язок між внутрішньою енергією, теплом і роботою можна представити рівнянням:

\[ΔU=q+w \label{5.4.1} \]

як показано на малюнку\(\PageIndex{1}\). Це одна з версій першого закону термодинаміки, і він показує, що внутрішня енергія системи змінюється через тепловий потік в або з системи (позитивний q - це тепловий потік в; негативний q - тепловий потік) або робота, виконана на або системою. Робота, w, позитивна, якщо вона виконана в системі, і негативна, якщо вона виконується системою.

Малюнок\(\PageIndex{1}\): Внутрішня енергія, U, системи може бути змінена тепловим потоком і роботою. Якщо тепло надходить в систему, q _in, або проводиться робота над системою, w _на, її внутрішня енергія збільшується, ΔU > 0. Якщо тепло витікає з системи, q _{виходить}, або робота виконується системою, w _by, її внутрішня енергія зменшується, ΔU < 0.

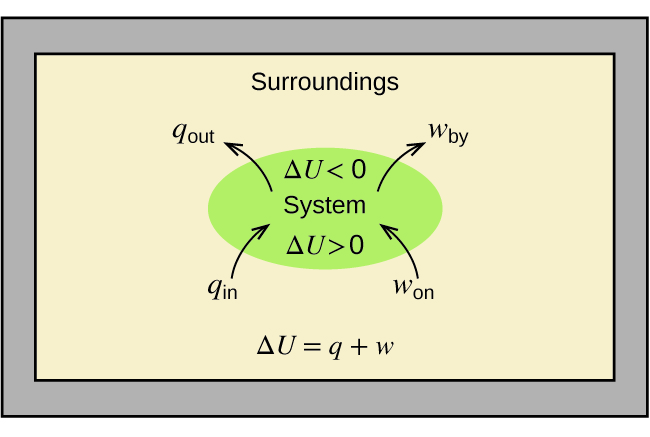
Тип роботи, який називається роботою з розширенням (або роботою за обсягом тиску), виникає, коли система відштовхує оточення проти стримуючого тиску або коли оточення стискає систему. Приклад цього відбувається під час роботи двигуна внутрішнього згоряння. Реакція бензину і кисню екзотермічна. Частина цієї енергії віддається як тепло, а деякі працюють штовхаючи поршень в циліндрі. Речовини, що беруть участь в реакції, - це система, а двигун і решта Всесвіту - це оточення. Система втрачає енергію як при нагріванні, так і при виконанні робіт над навколишнім середовищем, а її внутрішня енергія зменшується. (Двигун здатний тримати автомобіль в русі, оскільки цей процес повторюється багато разів на секунду під час роботи двигуна.) Як визначити обсяг робіт, пов'язаних з хімічним або фізичним зміною, ми розглянемо в розділі, присвяченому термодинаміці.

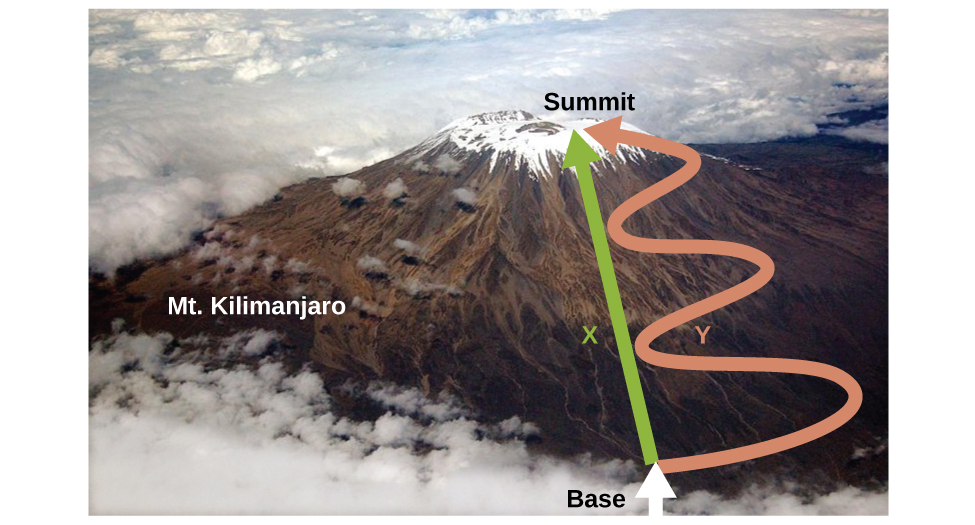
Як обговорювалося, зв'язок між внутрішньою енергією, теплом і роботою можна представити як Δ U = q + w. Внутрішня енергія - це тип величини, відомий як функція стану (або змінна стану), тоді як тепло та робота не є функціями стану. Значення функції стану залежить тільки від стану, в якому знаходиться система, а не від того, як цей стан досягається. Якщо величина не є функцією стану, то її значення залежить від того, як буде досягнуто стан. Прикладом функції стану є висота або висота. Якщо ви стоїте на вершині гори. Кіліманджаро, ви перебуваєте на висоті 5895 м, і неважливо, поїхали ви туди в похід або каталися на парашуті. Відстань, яку ви пройшли до вершини Кіліманджаро, однак, не є державною функцією. Піднятися на вершину можна було прямим маршрутом або більш кільцевим, кільцевим шляхом (рис.\(\PageIndex{2}\)). Пройдені відстані будуть відрізнятися (відстань не є функцією стану), але досягнута висота була б однаковою (висота - це функція стану).

Малюнок\(\PageIndex{2}\): Шляхи X і Y представляють два різних маршрути до вершини гори. Кіліманджаро Обидва мають однакову зміну висоти (висота або висота на горі є функцією стану; це не залежить від шляху), але вони мають дуже різні пройдені відстані (пройдена відстань не є функцією стану; це залежить від шляху). (кредит: модифікація роботи Пола Шафнера)

Аерофотознімок зображує вид на гору Кіліманджаро. Пряма зелена стрілка з позначкою X проводиться від терміну «база», написаного внизу гори, до терміна «Вершина», написаного на вершині гори. Інша стрілка з міткою Y малюється від основи до вершини поряд із зеленою стрілкою, але ця стрілка рожева і має три великі S-образні криві по довжині.

Хіміки зазвичай використовують властивість, відому як ентальпія (\(H\)) для опису термодинаміки хімічних та фізичних процесів. Ентальпія визначається як сума внутрішньої енергії системи (\(U\)) та математичного добутку її тиску (\(P\)) та обсягу (\(V\)):

\[H=U+PV \label{5.4.2} \]

Оскільки він походить від трьох функцій стану (\(U\),\(P\), і\(V\)), ентальпія також є функцією стану. Значення ентальпії для конкретних речовин неможливо виміряти безпосередньо; можна визначити лише зміни ентальпії для хімічних або фізичних процесів. Для процесів, що протікають при постійному тиску (загальна умова багатьох хімічних і фізичних змін), зміна ентальпії (\(ΔH\)) - це:

\[ΔH=ΔU+PΔV\label{5.4.3} \]

Математичний твір\(PΔV\) являє собою роботу (\(w\)), а саме, розширення або тиск об'ємної роботи, як зазначено. За їх визначеннями арифметичні знаки ΔV і w завжди будуть протилежні:

\[PΔV=−w \label{5.4.4} \]

Підстановка рівняння\ ref {5.4.4} та визначення внутрішньої енергії (Рівняння\ ref {5.4.1}) в Рівняння\ ref {5.4.3} дає:

\[ \begin{align} ΔH&=ΔU+PΔV \\[4pt] &=q_\ce{p}+\cancel{w}−\cancel{w} \\[4pt] &=q_\ce{p} \label{5.4.5} \end{align} \]

де\(q_p\) - теплота реакції в умовах постійного тиску.

І так, якщо хімічний або фізичний процес здійснюється при постійному тиску з єдиною виконаною роботою, викликаної розширенням або стисненням, то тепловий потік (\(q_\ce{p}\)) і зміна ентальпії (\(ΔH\)) для процесу рівні.

Тепло, що виділяється при роботі пальника Бунзена, дорівнює ентальпійній зміні реакції згоряння метану, що відбувається, оскільки воно відбувається при істотно постійному тиску атмосфери. З іншого боку, тепло, вироблене реакцією, виміряною в калориметрі бомби, не дорівнює\(ΔH\) тому, що закритий металевий контейнер постійного обсягу запобігає виникненню роботи з розширенням. Хіміки зазвичай проводять експерименти в нормальних атмосферних умовах, при постійному зовнішньому тиску з\(q = ΔH\), що робить ентальпію найбільш зручним вибором для визначення теплоти.

Наступні конвенції застосовуються, коли ми використовуємо\(ΔH\):

1. Хіміки використовують термохімічне рівняння для представлення змін як речовини, так і енергії. У термохімічному рівнянні зміна ентальпії реакції показана як значення Δ H після рівняння реакції. Ця\(ΔH\) величина вказує на кількість тепла, пов'язаного з реакцією за участю кількості молів реагентів і продуктів, як показано в хімічному рівнянні. Наприклад, розглянемо таке рівняння:\[\ce{H2(g) + 1/2 O2(g) ⟶ H2O (l)} \;\; ΔH=\mathrm{−286\:kJ} \label{5.4.6} \] Це рівняння вказує на те, що при зміні 1 моля газоподібного водню і 12 моль газу кисню при деякій температурі і тиску на 1 моль рідкої води при тій же температурі і тиску в навколишнє середовище виділяється 286 кДж тепла. Якщо коефіцієнти хімічного рівняння множаться на якийсь коефіцієнт, зміна ентальпії потрібно помножити на той самий коефіцієнт (ΔH - велика властивість).

\[\begin {align*} &\textrm{(two-fold increase in amounts)}\label{5.4.7}\\ &\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\hspace{20px}ΔH=\mathrm{2×(−286\:kJ)=−572\:kJ}\\ &\textrm{(two-fold decrease in amounts)}\\ &\frac{1}{2}\ce{H2}(g)+\dfrac{1}{4}\ce{O2}(g)⟶\frac{1}{2}\ce{H2O}(l)\hspace{20px}ΔH=\mathrm{\frac{1}{2}×(−286\:kJ)=−143\:kJ} \end {align*} \label{5.4.6B} \]

2. Зміна ентальпії реакції залежить від фізичного стану реагентів та продуктів реакції (чи є у нас гази, рідини, тверді речовини або водні розчини), тому вони повинні бути показані. Наприклад, при зміні 1 моль газу водню і 12 моль газу кисню на 1 моль рідкої води при однаковій температурі і тиску виділяється 286 кДж тепла. Якщо утворюється газоподібна вода, виділяється всього 242 кДж тепла.

\[\ce{ H2(g) + 1/2 O2(g) ⟶ H2O(g)} \;\;\; ΔH=\ce{−242\:kJ} \label{5.4.7B} \]

 

3. Від'ємне значення зміни ентальпії, Δ H, вказує на екзотермічну реакцію; позитивне значення Δ Н вказує на ендотермічну реакцію. Якщо напрямок хімічного рівняння зворотне, то змінюється арифметичний знак його Δ H (процес, ендотермічний в одному напрямку, екзотермічний в протилежному напрямку).

Приклад\(\PageIndex{1}\): Measurement of an Enthalpy Change

Коли 0,0500 моль HCl (aq) реагує з 0,0500 моль NaOH (aq), утворюючи 0,0500 моль NaCl (aq), утворюється 2,9 кДж тепла. Що таке ΔH, зміна ентальпії, на моль кислоти, що реагує, для кислотно-лужної реакції, що протікає в описаних умовах?

\[\ce{HCl (aq) + NaOH(aq) \rightarrow NaCl (aq) + H2O(l)} \nonumber \]

Рішення

Для реакції 0,0500 моль кислоти (HCl) q = −2,9 кДж. Це співвідношення

\[\mathrm{\dfrac{−2.9 \; kJ}{0.0500\; mol\; HCl}} \nonumber \]

може використовуватися як коефіцієнт перетворення для пошуку тепла, що утворюється, коли 1 моль HCl реагує:

\[ΔH =\mathrm{1\; \cancel{mol\; HCl} \times \dfrac{ −2.9\; kJ}{0.0500 \;\cancel{ mol\; HCl}} =−58\; kJ} \nonumber \]

Зміна ентальпії, коли 1 моль HCl реагує, становить −58 кДж. Оскільки це кількість молів у хімічному рівнянні, ми запишемо термохімічне рівняння як:

\[\ce{HCl}_{(aq)}+\ce{NaOH}_{(aq)}⟶\ce{NaCl}_{(aq)}+\ce{H_2O}_{(l)} \;\;\; ΔH=\mathrm{−58\;kJ} \nonumber \]

Вправа\(\PageIndex{1}\)

Коли 1,34 г Zn (s) реагує з 60,0 мл 0,750 М HCl (aq), утворюється 3,14 кДж тепла. Визначити зміну ентальпії на моль цинку, що реагує на реакцію:

\[ \ce{Zn}_{(s)}+\ce{2HCl}_{(aq)}⟶\ce{ZnCl}_{(aq)}+\ce{H}_{2(g)} \nonumber \]

Відповідь

ΔН = −153 кДж

Обов'язково враховуйте як стехіометрію, так і граничні реагенти при визначенні Δ Н для хімічної реакції.

Приклад\(\PageIndex{2}\): Another Example of the Measurement of an Enthalpy Change

Клейкий ведмідь містить 2,67 г сахарози, С ₁₂ Н ₂₂ О ₁₁. При його реакції з 7,19 г хлорату калію утворюється KClO ₃, 43,7 кДж тепла. Визначте зміну ентальпії для реакції

\[\ce{C12H22O11}(aq)+\ce{8KClO3}(aq)⟶\ce{12CO2}(g)+\ce{11H2O}(l)+\ce{8KCl}(aq) \nonumber \]

S рішення

У нас є\(\mathrm{2.67\:\cancel{g}×\dfrac{1\:mol}{342.3\:\cancel{g}}=0.00780\:mol\:C_{12}H_{22}O_{11}}\) доступні, і

\(\mathrm{7.19\:\cancel{g}×\dfrac{1\:mol}{122.5\:\cancel{g}}=0.0587\:mol\:KClO_3}\)доступні.

Так як

\(\mathrm{0.0587\:mol\:KClO_3×\dfrac{1\:mol\:\ce{C12H22O11}}{8\:mol\:KClO_3}=0.00734\:mol\:\ce{C12H22O11}}\)

потрібен, С ₁₂ Н ₂₂ О ₁₁ - надлишок реагенту, а KClO ₃ - граничний реагент.

Реакція використовує 8 моль KClO ₃, а коефіцієнт перетворення є\(\mathrm{\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}}\), так що ми маємо\(ΔH=\mathrm{8\:mol×\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}=−5960\:kJ}\). Зміна ентальпії для цієї реакції становить −5960 кДж, а термохімічне рівняння:

\[\ce{C12H22O11 + 8KClO3⟶12CO2 + 11H2O + 8KCl}\hspace{20px}ΔH=\ce{−5960\:kJ} \nonumber \]

Вправа\(\PageIndex{2}\)

Коли 1,42 г заліза вступає в реакцію з 1,80 г хлору, утворюється 3,22 г\(\ce{FeCl}_{2(s)}\) і 8,60 кДж тепла. Що таке зміна ентальпії для реакції, коли\(\ce{FeCl2(s)}\) виробляється 1 моль?

Відповідь

ΔН = −338 кДж

Зміни ентальпії, як правило, табличні для реакцій, в яких як реагенти, так і продукти знаходяться в однакових умовах. Стандартний стан - загальноприйнятий набір умов, що використовуються в якості орієнтиру для визначення властивостей при інших різних умовах. Для хіміків стандартний стан IUPAC відноситься до матеріалів під тиском 1 бар і розчинів при 1 М, і не вказує температуру (вона використовується теж). У багатьох термохімічних таблицях наведені значення зі стандартним станом в 1 атм. Оскільки Δ H реакції змінюється дуже мало при таких малих змінях тиску (1 бар = 0,987 атм), величини Δ H (за винятком найбільш точно виміряних значень) по суті однакові за обох наборів стандартних умов. Ми включимо надшифроване «o» в символ зміни ентальпії для позначення стандартного стану. Так як звичайна (але не технічно стандартна) температура становить 298,15 К, для позначення цієї температури ми будемо використовувати підстрокове «298». Таким чином, символ (\(ΔH^\circ_{298}\)) використовується для позначення зміни ентальпії процесу, що відбувається в цих умовах. (Символ Δ H використовується для позначення зміни ентальпії для реакції, що відбувається в нестандартних умовах.)

Зміни ентальпії для багатьох типів хімічних і фізичних процесів доступні в довідковій літературі, в тому числі для реакцій горіння, фазових переходів і реакцій формування. Коли ми обговорюємо ці величини, важливо звернути увагу на велику природу змін ентальпії та ентальпії. Оскільки зміна ентальпії для даної реакції пропорційна кількості речовин, що беруть участь, це може бути повідомлено на цій основі (тобто як Δ H для конкретних кількостей реагентів). Однак ми часто вважаємо корисніше розділити одну велику властивість (Δ H) на іншу (кількість речовини) і повідомити про інтенсивне значення Δ H, часто «нормалізоване» на моль основі. (Зверніть увагу, що це схоже на визначення інтенсивної властивості питомої теплоти від великої властивості теплоємності, як це було показано раніше.)

Ентальпія горіння

Стандартна ентальпія згоряння n (\(ΔH_C^\circ\)) - це зміна ентальпії, коли 1 моль речовини згорає (енергійно поєднується з киснем) в стандартних умовах стану; її іноді називають «теплотою згоряння». Наприклад, ентальпія згоряння етанолу, −1366,8 кДж/моль, - це кількість тепла, що утворюється при повному згорянні одного моля етанолу при 25 °С і тиску 1 атмосфери, що дає продукти також при 25 °С і 1 атм.

\[\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}+\ce{3H2O}(l)\hspace{20px}ΔH_{298}^\circ=\mathrm{−1366.8\: kJ} \label{5.4.8} \]

Ентальпії горіння для багатьох речовин були виміряні; деякі з них наведені в табл\(\PageIndex{1}\). Багато легкодоступні речовини з великими ентальпіями горіння використовуються в якості палива, включаючи водень, вуглець (як вугілля або деревне вугілля) і вуглеводні (сполуки, що містять тільки водень і вуглець), такі як метан, пропан і основні компоненти бензину.

Таблиця\(\PageIndex{1}\): Стандартні молярні ентальпії горіння

Речовина	Реакція горіння	Ентальпія горіння\(ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)\)
вуглець	\(\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−393.5
водню	\(\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−285.8
магній	\(\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−601.6
сірки	\(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» style="вирівнювання тексту: центр; ">−296.8
окис вуглецю	\(\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−283.0
метан	\(\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−890.8
ацетилену	\(\ce{C2H2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{2CO2}(g)+\ce{H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−1301.1
етанолу	\(\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−1366.8
метанол	\(\ce{CH3OH}(l)+\dfrac{3}{2}\ce{O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−726.1
ізооктан	\(\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)\)	\ (Δh_c^\ circ\ ліворуч (\ mathrm {\ dfrac {кДж} {моль}\ :при\ :25°C}\ праворуч)\)» стиль = "вирівнювання тексту: центр; ">−5461

Приклад\(\PageIndex{3}\): Using Enthalpy of Combustion

Як\(\PageIndex{3}\) випливає з малюнка, згоряння бензину є високоекзотермічним процесом. Визначимо приблизну кількість тепла, що виробляється при спалюванні 1,00 л бензину, припускаючи, що ентальпія згоряння бензину така ж, як у ізооктану, загального компонента бензину. Щільність ізооктану становить 0,692 г/мл.

Малюнок\(\PageIndex{3}\): Горіння бензину дуже екзотермічно. (кредит: модифікація роботи «AlexEagle» /Flickr)

Рішення

Починаючи з відомої кількості (1,00 л ізооктану), ми можемо виконувати перетворення між одиницями, поки не досягнемо бажаної кількості тепла або енергії. Ентальпія горіння ізооктану забезпечує одне з необхідних перетворень. Таблиця\(\PageIndex{1}\) дає це значення як −5460 кДж на 1 моль ізооктану (C ₈ H ₁₈).

Використовуючи ці дані,

\[\mathrm{1.00\:\cancel{L\:\ce{C8H18}}×\dfrac{1000\:\cancel{mL\:\ce{C8H18}}}{1\:\cancel{L\:\ce{C8H18}}}×\dfrac{0.692\:\cancel{g\:\ce{C8H18}}}{1\:\cancel{mL\:\ce{C8H18}}}×\dfrac{1\:\cancel{mol\:\ce{C8H18}}}{114\:\cancel{g\:\ce{C8H18}}}×\dfrac{−5460\:kJ}{1\:\cancel{mol\:\ce{C8H18}}}=−3.31×10^4\:kJ} \nonumber \]

При згорянні 1,00 л ізооктану виробляється 33 100 кДж тепла. (Цієї кількості енергії достатньо, щоб розтопити 99,2 кг, або близько 218 фунтів, льоду.)

Примітка: Якщо ви робите цей розрахунок по одному кроку за раз, ви знайдете:

\ (\ почати {вирівнювати*}
&\ матрм {1,00\ :Л\:\ ce {C8H18} 1.00×10^3\ :мл\:\ ce {C8H18}}\\
&\ матрм {1,00×10^3\ :мл\:\ ce {C8H18} 692\ :g\:\ ce {C8H18}\\
&\ математика {692\ :g\:\ ce {C8H18} 6.07\ :моль\:\ ce {C8H18}}\\
&\ математика {692\ :g\:\ ce {C8H18} −3,31×10^4\ :kJ}
\ end {вирівнювати*}\)

Вправа\(\PageIndex{3}\)

Скільки тепла виробляється при згорянні 125 г ацетилену?

Відповідь

6,25 × 10 ³ кДж

Нові енергетичні технології на основі водоростей (біопаливо)

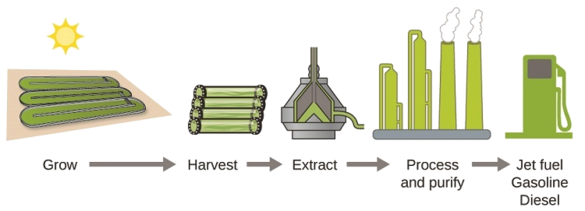
Оскільки запаси викопного палива зменшуються і стають дорожчими для видобутку, триває пошук запасних джерел палива на майбутнє. Серед найбільш перспективних біопалив - ті, що отримані з водоростей (рис.\(\PageIndex{4}\)). Використовувані види водоростей є нетоксичними, біологічно розкладаються та є одними з найбільш швидкозростаючих організмів у світі. Близько 50% ваги водоростей - це масло, яке можна легко перетворити на паливо, таке як біодизель. Водорості можуть дати 26 000 галонів біопалива на гектар - набагато більше енергії на акр, ніж інші культури. Деякі штами водоростей можуть процвітати в солонуватій воді, яка непридатна для вирощування інших культур. Водорості можуть виробляти біодизель, біобензин, етанол, бутанол, метан і навіть реактивне паливо.

Малюнок\(\PageIndex{4}\): (а) Крихітні водорості організми можна (б) вирощувати у великих кількостях і врешті-решт (в) перетворити на корисне паливо, таке як біодизель. (кредит а: модифікація роботи Міха Сіттіга; кредит b: модифікація роботи Роберта Кертона; кредит c: модифікація роботи Джона Вільямса)

За даними Міністерства енергетики США, лише 39 000 квадратних кілометрів (близько 0,4% сухопутної маси США або менше\(\dfrac{1}{7}\) площі, що використовується для вирощування кукурудзи) можуть виробляти достатню кількість водорослевого палива, щоб замінити все пальне на основі нафти, яке використовується в США. Вартість водорослевого палива стає все більш конкурентоспроможною - наприклад, ВПС США виробляють реактивне паливо з водоростей загальною вартістю менше 5 доларів за галон. Процес, що використовується для виробництва водоростей, полягає в наступному: вирощувати водорості (які використовують сонячне світло як джерело енергії та CO ₂ як сировину); збирати водорості; витягувати сполуки палива (або сполуки-попередники); процес за необхідності (наприклад, виконати реакцію переетерифікації, щоб зробити біодизель); очистити; і розподілити (рис.\(\PageIndex{5}\)).

Малюнок\(\PageIndex{5}\): Водорості перетворюють сонячне світло та вуглекислий газ у нафту, яку збирають, видобувають, очищують та перетворюють у різноманітні відновлювані види палива.

Стандартна ентальпія освіти

Стандартна ентальпія освіти\(ΔH^\circ_\ce{f}\) - це зміна ентальпії для реакції, при якій з вільних елементів утворюється рівно 1 моль чистої речовини в їх найбільш стійких станах при стандартних умовах стану. Ці значення особливо корисні для обчислення або прогнозування змін ентальпії для хімічних реакцій, які є непрактичними або небезпечними для проведення, або для процесів, для яких важко проводити вимірювання. Якщо у нас є значення для відповідних стандартних ентальпій освіти, ми можемо визначити зміну ентальпії для будь-якої реакції, яку ми будемо практикувати в наступному розділі про закон Гесса.

Стандартна ентальпія утворення СО ₂ (г) становить −393,5 кДж/моль. Це зміна ентальпії для екзотермічної реакції:

\[\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=−393.5\:\ce{kJ} \label{5.4.9} \]

починаючи з реагентів при тиску 1 атм і 25 °С (з вуглецем, присутнім у вигляді графіту, найбільш стабільною формою вуглецю в цих умовах) і закінчуючи одним молем СО ₂, також при 1 атм і 25 °С., Для діоксиду азоту\(\ce{NO}_{2(g)}\),\(ΔH^\circ_\ce{f}\) становить 33,2 кДж/моль. Це зміна ентальпії для реакції:

\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=+33.2\: \ce{kJ} \label{5.4.10} \]

Рівняння реакції з\(\frac{1}{2}\) молем N ₂ і 1 моль O ₂ є правильним у цьому випадку, оскільки стандартна ентальпія освіти завжди відноситься до 1 моль продукту, NO ₂ (g).

Таблицю стандартних ентальпій утворення багатьох поширених речовин ви знайдете в таблицях Т1 і Т2. Ці значення вказують на те, що реакції утворення варіюються від високоекзотермічних (наприклад, −2984 кДж/моль для утворення P ₄ O ₁₀) до сильно ендотермічних (наприклад, +226,7 кДж/моль для утворення ацетилену, C ₂ H ₂). За визначенням, стандартна ентальпія освіти елемента в його найбільш стійкому вигляді дорівнює нулю при стандартних умовах, що становить 1 атм для газів і 1 М для розчинів.

Приклад\(\PageIndex{4}\): Evaluating an Enthalpy of Formation

Озон, O ₃ (g), утворюється з кисню, O ₂ (g), шляхом ендотермічного процесу. Ультрафіолетове випромінювання є джерелом енергії, яка рухає цю реакцію у верхній атмосфері. Припускаючи, що і реагенти, і продукти реакції знаходяться в своїх стандартних станах, визначають стандартну ентальпію освіти, озону з\(ΔH^\circ_\ce{f}\) наступної інформації:

\[\ce{3O2}(g)⟶\ce{2O3}(g)\hspace{20px}ΔH^\circ_{298}=+286\: \ce{kJ} \nonumber \]

S olutio n\(ΔH^\circ_\ce{f}\) - зміна ентальпії для утворення одного моля речовини в його стандартному стані від елементів в їх стандартних станах. Таким чином,\(ΔH^\circ_\ce{f}\) для O ₃ (g) відбувається зміна ентальпії для реакції:

\[\dfrac{3}{2}\ce{O2}(g)⟶\ce{O3}(g) \nonumber \]

Для утворення 2 моль О ₃ (г),\(ΔH^\circ_{298}=+286\: \ce{kJ}\). Це співвідношення\(\mathrm{\left(\dfrac{286\:kJ}{2\:mol\:O_3}\right)}\), може бути використано як коефіцієнт перетворення для знаходження тепла, виробленого при утворенні 1 моль O ₃ (g), що є ентальпією освіти для O ₃ (g):

\[ΔH^\circ \ce{\:for\:1\:mole\: of\:O_3}(g)=\mathrm{1\:\cancel{mol\:O_3}×\dfrac{286\:kJ}{2\:\cancel{mol\:O_3}}=143\:kJ} \nonumber \]

Тому,\(ΔH^\circ_\ce{f}[\ce{O3}(g)]=\ce{+143\: kJ/mol}\).

Вправа\(\PageIndex{4}\)

Газ водню, Н ₂, вибухонебезпечно реагує з газоподібним хлором, Cl ₂, з утворенням хлористого водню, HCl (g). Що таке зміна ентальпії для реакції 1 моль Н ₂ (г) з 1 моль Cl ₂ (g), якщо і реагенти, і продукти знаходяться в стандартних умовах стану? Стандартна ентальпія освіти HCl (g) становить −92,3 кДж/моль.

Відповідь

Для реакції

\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{298}=\mathrm{−184.6\:kJ} \nonumber \]

Приклад\(\PageIndex{5}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)

Напишіть теплоту рівнянь реакції формування для:

1. \(\ce{C2H_5OH}_{(l)}\)
2. \(\ce{Ca_3(PO_4)}_{2(s)}\)

Рішення

Пам'ятаючи, що рівняння\(ΔH^\circ_\ce{f}\) реакції призначені для формування 1 моля сполуки зі складових його елементів в стандартних умовах, маємо:

1. \(\ce{2C}(s,\:\ce{graphite})+\ce{3H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OH}(l)\)
2. \(\ce{3Ca}(s)+\frac{1}{2}\ce{P4}(s)+\ce{4O2}(g)⟶\ce{Ca3(PO4)2}(s)\)

Примітка: Стандартним станом вуглецю є графіт, а фосфор існує як\(P_4\).

Вправа\(\PageIndex{5}\)

Напишіть теплоту рівнянь реакції формування для:

1. \(\ce{C_2H_5OC_2H}_{5(l)}\)
2. \(\ce{Na_2CO}_{3(s)}\)

Відповідь

\(\ce{4C}(s,\:\ce{graphite})+\ce{5H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OC2H5}(l)\);

Відповідь б

\(\ce{2Na}(s)+\ce{C}(s,\:\ce{graphite})+\dfrac{3}{2}\ce{O2}(g)⟶\ce{Na2CO3}(s)\)

Закон Гесса

Існує два способи визначити кількість тепла, що бере участь в хімічній зміні: виміряти його експериментально або обчислити з інших експериментально визначених змін ентальпії. Деякі реакції важко, якщо не неможливо, дослідити і зробити точні вимірювання для експериментально. І навіть коли реакцію не важко виконати або виміряти, зручно мати можливість визначити тепло, що бере участь у реакції, не виконуючи експеримент.

Цей тип обчислення зазвичай передбачає використання закону Гесса, який говорить: Якщо процес можна записати як суму декількох ступеневих процесів, зміна ентальпії загального процесу дорівнює сумі змін ентальпії різних кроків. Закон Гесса діє, оскільки ентальпія є функцією стану: зміни ентальпії залежать лише від того, де починається і закінчується хімічний процес, але не від шляху, який він проходить від початку до кінця. Наприклад, ми можемо думати про реакцію вуглецю з киснем з утворенням вуглекислого газу як відбувається безпосередньо, так і двоетапним процесом. Безпосередній процес пишеться:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)}\;\;\;ΔH^∘_{298}=\mathrm{−394\;kJ} \label{ 5.4.11} \]

При двоетапному процесі спочатку утворюється чадний газ:

\[\ce{C}_{(s)}+\dfrac{1}{2}\ce{O}_{2(g)}⟶\ce{CO}_{(g)}\;\;\;ΔH^∘_{298}=\mathrm{−111\;kJ} \label{ 5.4.12} \]

Потім чадний газ реагує далі з утворенням вуглекислого газу:

\[\ce{CO} {(g)}+\dfrac{1}{2}\ce{O2}(g)⟶\ce{CO}_2 {(g)}\;\;\;ΔH^∘_{298}=\mathrm{−283\;kJ} \label{ 5.4.13} \]

Рівняння, що описує загальну реакцію, є сумою цих двох хімічних змін:

\[\begin {align*} &\textrm{Step 1:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)\\ &\underline{\textrm{Step 2:} \:\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)}\\ &\textrm{Sum:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)+\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)+\ce{CO2}(g) \end {align*} \label{5.4.14} \]

Оскільки СО, вироблений на кроці 1, споживається на кроці 2, чиста зміна становить:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)} \label{5.4.15} \]

Згідно із законом Гесса, зміна ентальпії реакції дорівнюватиме сумі ентальпійних змін ступенів. Ми можемо застосувати дані експериментальних ентальпій горіння в таблиці,\(\PageIndex{1}\) щоб знайти зміну ентальпії всієї реакції з двох її етапів:

\ [\ почати {вирівнювати*}
&\ ce {C} (s) +\ розриву {1} {2}\ ce {O2} (g) ⟶\ ce {CO} (г) &&ΔH^\ circ_ {298} =\ mathrm {−111\ :KJ}\\
&\ ce {CO} (г) +\ frac {1} {2}\ ce O2} (g) ⟶\ ce {CO2} (г) &&ΔH^\ circ_ {298} =\ mathrm {−283\ :кДж}\\
&\ overline {\ ce {C} (s) +\ ce {O2} (g) ⟶\ ce {CO2} (г)\ hspace {25px}} & ; &\ верхня лінія {ΔH^\ circ_ {298} =\ mathrm {−394\ :kJ}}
\ кінець {align*}\ мітка {5.4.16}\]

Результат показаний на малюнку\(\PageIndex{6}\). Ми бачимо, що ΔH загальної реакції однакова, чи відбувається вона в один крок або два. Ця знахідка (загальний ΔH для реакції = сума значень Δ H для «кроків» реакції в загальній реакції) вірно в цілому для хімічних і фізичних процесів.

Малюнок\(\PageIndex{6}\): Утворення СО ₂ (g) з його елементів можна розглядати як відбувається в два етапи, які підсумовуються загальній реакції, як описано законом Гесса. Горизонтальні сині лінії представляють ентальпії. Для екзотермічного процесу продукти мають меншу ентальпію, ніж реагенти.

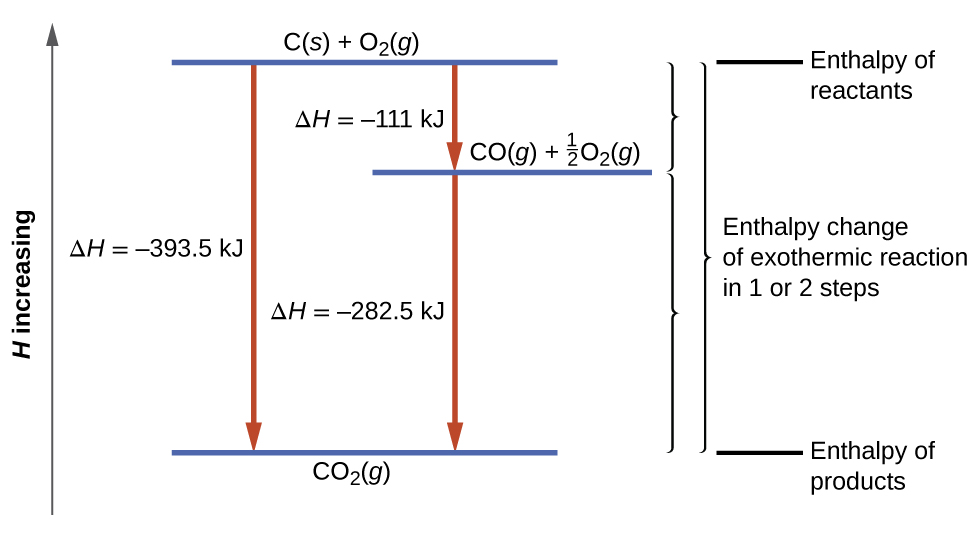
Перш ніж ми далі практикуємо використання закону Гесса, згадаємо дві важливі особливості Δ H.

1. Δ Н прямо пропорційна кількостям реагентів або продуктів. Наприклад, зміна ентальпії для реакції, що утворює 1 моль NO ₂ (g), становить +33,2 кДж:\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{+33.2\: kJ} \label{5.4.17} \]

   При утворенні _{2 родимок NO 2} (в два рази більше) Δ Н буде в два рази більше:\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g)\hspace{20px}ΔH=\mathrm{+66.4\: kJ} \label{5.4.18} \]

   Загалом, якщо помножити або розділити рівняння на число, то зміна ентальпії також слід помножити або розділити на одне і те ж число.

2. Δ H для реакції в одному напрямку дорівнює за величиною і протилежний за знаком Δ H для реакції в зворотному напрямку. Наприклад, враховуючи, що:\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH=\mathrm{−184.6\:kJ} \label{5.4.19} \]

   Потім для «зворотної» реакції зміна ентальпії також «зворотне»:\[\ce{2HCl}(g)⟶\ce{H2}(g)+\ce{Cl2}(g)\hspace{20px}ΔH=\mathrm{+184.6\: kJ} \label{5.4.20} \]

Приклад\(\PageIndex{6}\): Stepwise Calculation of \(ΔH^\circ_\ce{f}\)

Використовуючи закон Гесса Визначте ентальпію утворення FeCl ₃ (s) від ентальпійних змін наступного двоетапного процесу, що відбувається в стандартних умовах стану:\(ΔH^\circ_\ce{f}\)

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{20px}ΔH°=\mathrm{−341.8\:kJ} \nonumber \]

\[\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm \nonumber{−57.7\:kJ} \nonumber \]

Рішення

Ми намагаємося знайти стандартну ентальпію утворення FeCl3 (s), яка дорівнює ΔH° для реакції:

\[\ce{Fe}(s)+\frac{3}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH^\circ_\ce{f}=\:? \nonumber \]

Дивлячись на реакції, ми бачимо, що реакція, для якої ми хочемо знайти Δ H°, є сумою двох реакцій з відомими значеннями Δ H, тому ми повинні підсумувати їх Δ H s:

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{59px}ΔH°=\mathrm{−341.8\:kJ}\\ \underline{\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm{−57.7\:kJ}}\\ \ce{Fe}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{43px}ΔH°=\mathrm{−399.5\:kJ} \nonumber \]

Ентальпія освіти FeCl ₃ (s) становить −399,5 кДж/моль.\(ΔH^\circ_\ce{f}\)

Вправа\(\PageIndex{6}\)

Обчисліть ΔH для процесу:

\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g) \nonumber \]

з наступної інформації:

\[\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g)\hspace{20px}ΔH=\mathrm{180.5\:kJ} \nonumber \]

\[\ce{NO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{−57.06\:kJ} \nonumber \]

Відповідь

66,4 кДж

Ось менш простий приклад, який ілюструє розумовий процес, який бере участь у вирішенні багатьох юридичних проблем Гесса. Він показує, як ми можемо знайти багато стандартних ентальпій освіти (та інших значень Δ H), якщо їх важко визначити експериментально.

Приклад\(\PageIndex{7}\): A More Challenging Problem

Використовуючи закон Гесса, монофторид хлору може реагувати з фтором, утворюючи трифторид хлору:

(i)\(\ce{ClF}(g)+\ce{F2}(g)⟶\ce{ClF3}(g)\hspace{20px}ΔH°=\:?\)

Використовуйте реакції тут, щоб визначити ΔH° для реакції (i):

(ii)\(\ce{2OF2}(g)⟶\ce{O2}(g)+\ce{2F2}(g)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−49.4\:kJ}\)

(iii)\(\ce{2ClF}(g)+\ce{O2}(g)⟶\ce{Cl2O}(g)+\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{+205.6\: kJ}\)

(iv)\(\ce{ClF3}(g)+\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+266.7\: kJ}\)

Рішення

Наша мета полягає в тому, щоб маніпулювати та поєднувати реакції (ii), (iii) та (iv) таким чином, щоб вони складалися до реакції (i). Йдучи зліва направо в (i), ми спочатку бачимо,\(\ce{ClF}_{(g)}\) що потрібен як реагент. Це можна отримати шляхом множення реакції (iii) на\(\frac{1}{2}\), що означає, що зміна ΔH° також множиться на\(\frac{1}{2}\):

\[\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)\hspace{20px} ΔH°=\frac{1}{2}(205.6)=+102.8\: \ce{kJ} \nonumber \]

Далі ми бачимо,\(\ce{F_2}\) що також потрібен як реагент. Щоб отримати це, зворотна і вдвічі реакція (ii), що означає, що ΔH° змінюється знак і зменшується вдвічі:

\[\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)\hspace{20px}ΔH°=+24.7\: \ce{kJ} \nonumber \]

Щоб отримати CLF ₃ як добуток, зворотний (iv), змінюючи знак ΔH°:

\[\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)⟶\ce{ClF3}(g)+\ce{O2}(g)\hspace{20px}ΔH°=\mathrm{−266.7\: kJ} \nonumber \]

Тепер перевірте, щоб переконатися, що ці реакції складаються з реакції, яку ми хочемо:

\ [\ почати {вирівнювати*}
&\ ce {CLF} (г) +\ розрив {1} {2}\ ce {O2} (г) ˈFRAC {1} {2}\ ce {Cl2O} (г) +\ frac {1} {2}\ ce {OF2} (г) &&ΔH°=\ mathrm {+102.8\ кДж}\\
&\ розрив {1} {2}\ ce {O2} (г) +\ ce {F2} (г) ⟶\ ce {OF2} (г) &&ΔH°=\ матхрм {+24.7\: кДж}\\
&\ frac {1} {2}\ ce {Cl2O} (г) +\ dfrac {3} {2}\ се {OF2} (g) ⟶\ ce {ClF3} (g) +\ ce {O2} (г) &&ΔH°=\ математика {−266.7\ :кДж}\\
&\ оверлайн {\ ce {CLF} (г) +\ ce {F2} ˈce {CLF3} (г)\ hspace {130px}} &\ над лінією {ΔН°=\ математика {−139.2\ :kJ}}
\ кінець {вирівнює*}\ номер\]

Реагенти\(\frac{1}{2}\ce{O2}\) та\(\frac{1}{2}\ce{O2}\) скасовують продукт O ₂; продукт\(\frac{1}{2}\ce{Cl2O}\) скасовує реагент\(\frac{1}{2}\ce{Cl2O}\); а реагент\(\dfrac{3}{2}\ce{OF2}\) скасовується продуктами\(\frac{1}{2}\ce{OF2}\) та OF ₂. Це залишає тільки реагенти CLF (g) і F ₂ (g) і продукт ClF ₃ (g), які є те, що ми хочемо. Оскільки підсумовування цих трьох модифікованих реакцій дає реакцію, що цікавить, підсумовування трьох модифікованих величин ΔH° дасть бажаний ΔH°:

\(ΔH°=\mathrm{(+102.8\:kJ)+(24.7\:kJ)+(−266.7\:kJ)=−139.2\:kJ}\)

Вправа\(\PageIndex{7}\)

Хлорид алюмінію може утворюватися з його елементів:

(i)\(\ce{2Al}(s)+\ce{3Cl2}(g)⟶\ce{2AlCl3}(s)\hspace{20px}ΔH°=\:?\)

Використовуйте реакції тут, щоб визначити ΔH° для реакції (i):

(ii)\(\ce{HCl}(g)⟶\ce{HCl}(aq)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−74.8\:kJ}\)

(iii)\(\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{−185\:kJ}\)

(iv)\(\ce{AlCl3}(aq)⟶\ce{AlCl3}(s)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+323\:kJ/mol}\)

(v)\(\ce{2Al}(s)+\ce{6HCl}(aq)⟶\ce{2AlCl3}(aq)+\ce{3H2}(g)\hspace{20px}ΔH^\circ_{(v)}=\mathrm{−1049\:kJ}\)

Відповідь

−1407 кДж

Ми також можемо використовувати закон Гесса для визначення зміни ентальпії будь-якої реакції, якщо є відповідні ентальпії утворення реагентів і продуктів. Ми розглядаємо ступінчасті реакції: (i) розклади реагентів на їх складові елементи (для яких зміни ентальпії пропорційні негативним ентальпіям утворення реагентів), а потім (ii) повторні комбінації елементів для отримання продуктів (з ентальпією зміни, пропорційні ентальпіям утворення виробів). Отже, стандартна зміна ентальпії загальної реакції дорівнює: (ii) сумі стандартних ентальпій утворення всіх продуктів плюс (i) сума негативів стандартних ентальпій утворення реагентів. Зазвичай це трохи переставляється, щоб записати наступним чином,\(\sum\) представляючи «суму» та n, що стоїть для стехіометричних коефіцієнтів:

\[ΔH^\circ_\ce{reaction}=\sum n×ΔH^\circ_\ce{f}\ce{(products)}−\sum n×ΔH^\circ_\ce{f}\ce{(reactants)} \label{5.4.20B} \]

Наступний приклад детально показує, чому це рівняння є дійсним, і як його використовувати для обчислення зміни ентальпії для реакції, що цікавить.

Приклад\(\PageIndex{8}\): Using Hess’s Law

Що таке стандартна зміна ентальпії для реакції:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\hspace{20px}ΔH°=\:? \nonumber \]

Рішення 1. Використання рівняння

Крім того, ми могли б використовувати спеціальну форму закону Гесса, наведену раніше:

\[ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)} \nonumber \]

\[\begin {align*} &=\mathrm{\left[2\:\cancel{mol\:HNO_3}×\dfrac{−207.4\:kJ}{\cancel{mol\:HNO_3\:(\mathit{aq})}}+1\:\cancel{mol\: NO\:(\mathit{g})}×\dfrac{+90.2\: kJ}{\cancel{mol\: NO\:(\mathit{g})}}\right]}\\ &\mathrm{\:−\,\left[3\:\cancel{mol\:NO_2(\mathit{g})}×\dfrac{+33.2\: kJ}{\cancel{mol\:NO_2\:(\mathit{g})}}+1\:\cancel{mol\:H_2O\:(\mathit{l})}×\dfrac{−285.8\:kJ}{\cancel{mol\:H_2O\:(\mathit{l})}}\right]}\\ &=\mathrm{2(−207.4\:kJ)+1(+90.2\: kJ)−3(+33.2\: kJ)−1(−285.8\:kJ)}\\ &=\mathrm{−138.4\:kJ}\end {align*} \nonumber \]

S Рішення 2: Підтримуючи, чому загальне рівняння є дійсним

Ми можемо записати цю реакцію як суму розкладень 3NO ₂ (g) і 1H ₂ O (l) на їх складові елементи, так і утворення 2 HNO ₃ (aq) і 1 NO (g) з їх складових елементів. Виписуючи ці реакції, і відзначаючи їх зв'язок зі\(ΔH^\circ_\ce{f}\) значеннями для цих сполук (з таблиць Т1 і Т2), ми маємо:

\[\ce{3NO2}(g)⟶ \dfrac{3}{2} \ce{N2}(g)+ 3 \ce{O2}(g)\hspace{20px}ΔH^\circ_{1}=\mathrm{−99.6\:kJ} \nonumber \]

\[\ce{H2O}(l)⟶\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)\hspace{20px}ΔH^\circ_{2}=+285.8\: \ce{kJ}\:[−1×ΔH^\circ_\ce{f}(\ce{H2O})] \nonumber \]

\[\ce{H2}(g)+\ce{N2}(g)+ 3 \ce{O2}(g)⟶\ce{2HNO3}(aq)\hspace{20px}ΔH^\circ_{3}=−414.8\:kJ\:[2×ΔH^\circ_\ce{f}(\ce{HNO3 \nonumber})] \nonumber \]

\[\frac{1}{2}\ce{N2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO}(g)\hspace{20px}ΔH^\circ \nonumber_{4}=+90.2\: \ce{kJ}\:[1×(\ce{NO})] \nonumber \]

Підсумовування цих рівнянь реакції дає цікаву для нас реакцію:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g) \nonumber \]

Підсумовування їх ентальпійних змін дає значення, яке ми хочемо визначити:

\[\begin {align*} ΔH^\circ_\ce{rxn}&=ΔH^\circ_1+ΔH^\circ_2+ΔH^\circ_3+ΔH^\circ_4=\mathrm{(−99.6\:kJ)+(+285.8\: kJ)+(−414.8\:kJ)+(+90.2\: kJ)}\\ &=\mathrm{−138.4\:kJ} \end {align*} \nonumber \]

Отже, стандартна зміна ентальпії для цієї реакції становить Δ H° = −138,4 кДж.

Відзначимо, що такий результат був отриманий шляхом:

1. \(ΔH^\circ_\ce{f}\)множення кожного виробу на його стехіометричний коефіцієнт і підсумовуючи ці значення,
2. множивши кожен\(ΔH^\circ_\ce{f}\) реагент на його стехіометричний коефіцієнт і підсумовуючи ці значення, а потім
3. віднімання результату, знайденого на кроці 2, з результату, знайденого на кроці 1.

Це також процедура використання загального рівняння, як показано на малюнку.

Вправа\(\PageIndex{8}\)

Розрахуйте теплоту згоряння 1 моль етанолу, С ₂ Н ₅ ОН (л), коли утворюються Н ₂ О (л) і СО ₂ (г). Використовують такі ентальпії освіти: C ₂ H ₅ OH (l), −278 кДж/моль; H ₂ O (л), −286 кДж/моль; і CO ₂ (g), −394 кДж/моль.

Відповідь

−1368 кДж/моль

Резюме

Якщо хімічна зміна здійснюється при постійному тиску і єдина виконана робота викликана розширенням або стисненням, q для зміни називається зміною ентальпії з символом Δ H, або\(ΔH^\circ_{298}\) для реакцій, що відбуваються в стандартних умовах стану. Значення Δ Н для реакції в одному напрямку дорівнює за величиною, але протилежне за знаком, Δ Н для реакції в протилежному напрямку, а Δ H прямо пропорційно кількості реагентів і продуктів. Приклади змін ентальпії включають ентальпію горіння, ентальпія плавлення, ентальпія випаровування та стандартна ентальпія освіти. Стандартна ентальпія освіти - це зміна ентальпії\(ΔH^\circ_\ce{f}\), що супроводжує утворення 1 моль речовини з елементів в їх найбільш стабільних станах при 1 бар (стандартний стан). Багато процесів здійснюються при 298.15 К. Якщо ентальпії освіти доступні для реагентів і продуктів реакції, зміна ентальпії може бути розрахована за законом Гесса: Якщо процес можна записати як суму декількох ступеневих процесів, зміна ентальпії загального процесу дорівнює сумі змін ентальпії різних кроків.

Ключові рівняння

• \(ΔU=q+w\)
• \(ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}\)

Виноски

1. 1 Докладніше про водоросне паливо див. www.theguardian.com/environme... n-fuel-problem.

Глосарій

хімічна термодинаміка

область науки, яка займається взаємозв'язками між теплом, роботою та всіма формами енергії, пов'язаними з хімічними та фізичними процесами

ентальпія (Н)

сума внутрішньої енергії системи та математичний добуток її тиску та об'єму

зміна ентальпії (Δ H)

тепло, що виділяється або поглинається системою під постійним тиском під час хімічного або фізичного процесу

робота по розширенню (напірно-об'ємна робота)

робота, виконана як система розширюється або стискається проти зовнішнього тиску

перший закон термодинаміки

внутрішня енергія системи змінюється внаслідок теплового потоку в системі або поза нею або роботи, виконаної на або за допомогою системи

Закон Гесса

якщо процес може бути представлений у вигляді суми декількох кроків, зміна ентальпії процесу дорівнює сумі ентальпійних змін кроків

вуглеводнів

з'єднання, що складається тільки з водню і вуглецю; основний компонент викопного палива

внутрішня енергія (U)

всього всіх можливих видів енергії, присутніх у речовині або речовин

стандартна ентальпія горіння (\(ΔH^\circ_\ce{c}\))

тепло, що виділяється, коли один моль з'єднання піддається повному згорянню в стандартних умовах

стандартна ентальпія освіти (\(ΔH^\circ_\ce{f}\))

ентальпійна зміна хімічної реакції, при якій з її елементів утворюється 1 моль чистої речовини в їх найбільш стійких станах в умовах стандартного стану

стандарт держава

сукупність фізичних умов, прийнятих як загальні еталонні умови для повідомлення про термодинамічні властивості; 1 бар тиску та розчинів при 1 молярній концентрації, як правило, при температурі 298,15 К

держава функція

властивість залежно лише від стану системи, а не від шляху досягнення цього стану