14.2: Перший закон термодинаміки

Цілі навчання

Переконайтеся, що ви добре розумієте наступні основні поняття:

• Визначте: систему, оточення, властивості стану, зміну стану (як обчислюється останнє).
• Випишіть рівняння, яке визначає Перший Закон, і поясніть його фізичний сенс.
• Опишіть значення шляху в термодинаміці та те, як він пов'язаний з функціями стану.
• Прокоментуйте значення напірно-об'ємної роботи: як він розраховується? Які види хімічних реакцій передбачають роботу P-V?
• Визначте ізотермічні та адіабатичні процеси, і наведіть приклади кожного.
• На прикладі розширення газу констатувати принципову відмінність між оборотними та незворотними змінами з точки зору системи + оточення.
• Поясніть, як зміна ентальпії відноситься до внутрішньої енергії, і як її можна спостерігати експериментально.
• Визначте теплоємність; поясніть її фізичне значення, і чому існує різниця між С _р і С _v.

«Енергію неможливо створити або знищити» — цей фундаментальний закон природи, більш відомий як збереження енергії, знайомий кожному, хто вивчав науку. Під більш офіційною назвою Перший закон термодинаміки він регулює всі аспекти енергетики в науці та інженерних додатках. Особливе значення в хімії виникає через те, що практично всі хімічні реакції супроводжуються поглинанням або виділенням енергії. Однією з цікавих речей про термодинаміку є те, що, хоча вона стосується матерії, вона не робить припущень про мікроскопічну природу цієї матерії. Термодинаміка стосується матерії в макроскопічному сенсі; це було б справедливо, навіть якщо атомна теорія матерії була неправильною. Це важлива якість, оскільки це означає, що міркування, засновані на термодинаміці, навряд чи потребують змін, оскільки з'являться нові факти про атомну структуру та атомні взаємодії.

Термодинамічний погляд на світ

У термодинаміці ми повинні бути дуже точними у вживанні певних слів. Два найважливіших з них - система та оточення. Термодинамічна система - це та частина світу, на яку ми направляємо свою увагу. Все, що не є частиною системи, становить оточення. Система і оточення розділені межею.

Якщо наша система - це один моль газу в ємності, то межа - це просто внутрішня стінка самої ємності. Межа не повинна бути фізичним бар'єром; наприклад, якщо наша система є фабрикою чи лісом, то межа може бути там, де ми хочемо її визначити. Ми навіть можемо зосередити свою увагу на розчинених іонами у водному розчині солі, залишаючи молекули води як частину навколишнього середовища. Єдина властивість, якою повинна володіти межа, полягає в тому, що вона повинна бути чітко визначена, тому ми можемо однозначно сказати, чи є дана частина світу в нашій системі чи в оточенні.

Якщо матерія не здатна пройти через кордон, то система, як кажуть, закрита; інакше вона відкрита. Закрита система все ще може обмінюватися енергією з навколишнім середовищем, якщо система не є ізольованою, і в цьому випадку ні матерія, ні енергія не можуть пройти через межу. Чай у закритій пляшці Thermos наближається до закритої системи протягом короткого інтервалу часу.

Властивості системи - це такі величини, як тиск, об'єм, температура та її склад, які в принципі вимірюються і здатні приймати певні значення. Звичайно, існує багато властивостей, крім згаданих вище; щільність та теплопровідність - два приклади. Однак тиск, об'єм і температура мають особливе значення, оскільки вони визначають значення всіх інших властивостей; тому вони відомі як властивості стану, тому що якщо їх значення відомі, то система знаходиться в певному стані.

Маючи справу з термодинамікою, ми повинні мати можливість однозначно визначити зміну стану системи, коли вона проходить певний процес. Це робиться шляхом вказівки змін у значеннях різних властивостей стану за допомогою символу Δ (дельта), як показано тут для зміни обсягу:

\[ΔV = V_{final} – V_{initial} \label{1-1}\]

Ми можемо обчислити подібні дельта-значення для змін у P, V, n _i (кількість молів компонента i), а інші властивості стану ми зустрінемо пізніше.

Внутрішня енергія - це просто сукупність всіх форм кінетичної і потенційної енергії системи. Термодинаміка не робить різниці між цими двома формами енергії і вона не передбачає існування атомів і молекул. Але оскільки ми вивчаємо термодинаміку в контексті хімії, то можемо дозволити собі відійти від «чистої» термодинаміки досить, щоб вказати, що внутрішня енергія - це сума кінетичної енергії руху молекул, а потенційна енергія представлена хімічними зв'язками між атомами. і будь-які інші міжмолекулярні сили, які можуть бути оперативними.

Як ми можемо дізнатися, скільки внутрішньої енергії володіє система? Відповідь полягає в тому, що ми не можемо, принаймні, не на абсолютній основі; всі масштаби енергії довільні. Найкраще, що ми можемо зробити, це виміряти зміни в енергії. Однак ми абсолютно вільні визначити нульову енергію як енергію системи в якомусь довільному опорному стані, а потім говоримо, що внутрішня енергія системи в будь-якому іншому стані - це різниця енергій системи в цих двох різних станах.

Перший закон термодинаміки

Цей закон є одним з найбільш фундаментальних принципів фізичного світу. Також відомий як Закон збереження енергії, він стверджує, що енергія не може бути створена або знищена; вона може бути лише перерозподілена або змінена з однієї форми в іншу. Спосіб вираження цього закону, який, як правило, є більш корисним у хімії, полягає в тому, що будь-яка зміна внутрішньої енергії системи задається сумою тепла q, що протікає через її межі, і роботою w, виконаної над системою оточенням.

\[ΔU = q + w \label{2-1}\]

Це говорить про те, що існує два види процесів, тепло і робота, які можуть призвести до зміни внутрішньої енергії системи. Оскільки і тепло, і роботу можна виміряти та кількісно оцінити, це те саме, що сказати, що будь-яка зміна енергії системи повинна призвести до відповідної зміни енергії світу поза системою - іншими словами, енергія не може бути створена або знищена.

Існує важливий знак конвенції про тепло і роботу, які ви повинні знати. Якщо тепло надходить в систему або оточення, щоб зробити роботу над нею, внутрішня енергія збільшується, а знак q або w позитивний. І навпаки, тепловий потік з системи або робота, виконана системою, буде за рахунок внутрішньої енергії, а тому буде негативним. (Зверніть увагу, що це протилежність конвенції про знак, яка зазвичай використовувалася в більшій частині літератури до 1970 року.) Повне значення рівняння\(\ref{2-1}\) неможливо зрозуміти, не розуміючи, що U є функцією стану. Це означає, що задана зміна внутрішньої енергії Δ U може слідувати нескінченній різноманітності шляхів, відповідних всім можливим комбінаціям q і w, які можуть скласти до заданого значення Δ U.

Як простий приклад того, як цей принцип може спростити наше розуміння змін, розглянемо дві однакові ємності з водою спочатку однакової температури. Поміщаємо полум'я під одним, поки його температура не підвищиться на 1°C, воду в іншій ємності інтенсивно перемішують, поки її температура не збільшиться на таку ж кількість. Зараз не існує фізичного тесту, за допомогою якого можна було б визначити, яка проба води була прогріта, виконуючи на ній роботи, дозволяючи теплоті надходити в неї, або за допомогою якоїсь комбінації двох процесів. Іншими словами, немає підстав говорити про те, що один зразок води тепер містить більше «роботи», а інший більше «тепла». Єдине, що ми можемо знати напевно, це те, що обидві проби зазнали однакових збільшень внутрішньої енергії, і визначити величину можна просто шляхом вимірювання підвищення температури води.

Тисково-об'ємна робота

Вид робіт, найчастіше пов'язаний з хімічними змінами, відбувається при зміні обсягу системи внаслідок зникнення або утворення газоподібних речовин. Це іноді називають розширенням роботи або PV -роботою, і це найлегше зрозуміти, посилаючись на найпростішу форму матерії, з якою ми можемо мати справу, гіпотетичний ідеальний газ.

На малюнку показано кількість газу, укладеного в циліндрі за допомогою рухомого поршня. Ваги, розміщені зверху на поршень, надають силу f над площею поперечного перерізу A, створюючи тиск P = f/A, який точно протистоїть тиску газу, так що поршень залишається нерухомим. Тепер припустимо, що ми трохи нагріваємо газ; згідно із законом Чарльза, це призведе до розширення газу, тому поршень буде змушений вгору на відстань Δ x. Так як цьому руху протистоїть сила f, то величина роботи f Δ x буде виконуватися газом на поршні. За умовністю робота, виконана системою (в даному випадку газом) над навколишнім середовищем негативна, тому робота дається

\[w = – f Δx \label{3-1}\]

Маючи справу з газом, зручно думати з точки зору більш відповідних величин тиску і обсягу, а не сили і відстані. Ми можемо досягти цього, помноживши другий термін на A/A, що, звичайно, залишає його незмінним:

\[ w = -f Δx \dfrac{A}{A} \label{3-2}\]

Групуючи терміни по-іншому, але все одно нічого не змінюючи, отримуємо

\[ w = -\dfrac{f}{A} Δx A \label{3-3}\]

Оскільки тиск - це сила на одиницю площі, а добуток довжини А і площі має розміри об'єму, цей вираз стає

\[w = –P ΔV \label{3-4}\]

Важливо відзначити, що хоча\(P\) і\(V\) є державними функціями, робота не є (тому ми позначаємо її нижнім регістром w.) Як показано далі нижче, кількість виконаної роботи буде залежати від того, чи реалізується однакова зміна чистого обсягу за один крок (шляхом встановлення зовнішнього тиску на кінцевий тиск P), або в кілька етапів шляхом регулювання стримуючого тиску на газ до послідовно менших значень наближається до кінцевого значення\(P\).

Приклад\(\PageIndex{1}\)

Знайти обсяг виконаної роботи на околицях, коли 1 літр ідеального газу, спочатку при тиску в 10 атм, допускається розширювати при постійній температурі до 10 л на:

1. зниження зовнішнього тиску до 1 атм за один прийом,
2. зниження\(P\) спочатку до 5 атм, а потім до 1 атм,
3. дозволяючи газу розширюватися в евакуйоване простір, тому його загальний обсяг становить 10 літрів.

Рішення

По-перше, зверніть увагу\(ΔV\), що th at, який є функцією стану, однаковий для кожного шляху:

\[V_2 = (10/1) × (1 L) = 10 L\]

так

\[ΔV = 9\; L\]

Для шляху (a)

w = — (1 атм) × (9 л) = —9 L-атм.

Для шляху (б) робота розраховується для кожного етапу окремо:

w = — (5 атм) × (2—1 л) — (1 атм) × (10—2 л) = —13 L-атм

Для шляху (c) процес буде здійснюватися шляхом видалення всіх ваг з поршня на малюнку,\(\PageIndex{1}\) так що у газу розширюється до 10 л проти нульового зовнішнього тиску. У цьому випадку w = (0 атм) × 9 L = 0; тобто ніякої роботи не робиться, оскільки немає сили протистояти розширенню.

Адіабатичні та ізотермічні процеси

Коли газ розширюється, він працює над навколишнім середовищем; стиснення газу до меншого обсягу аналогічно вимагає, щоб оточення виконувало роботу на газі. Якщо газ термічно ізольований від навколишнього середовища, то процес, як кажуть, відбувається адіабатично. При адіабатичній зміні q = 0, тому Перший Закон стає Δ U = 0 + w. Оскільки температура газу змінюється разом з його внутрішньою енергією, випливає, що адіабатичне стиснення газу призведе до його нагрівання, тоді як адіабатичне розширення призведе до охолодження.

На відміну від цього, розгляньте газ, якому дозволяється повільно виходити з ємності, зануреної в ванну з постійною температурою. Коли газ розширюється, він працює на навколишнє середовище і, отже, має тенденцію до охолодження, але тепловий градієнт, який призводить до того, що тепло проходить в газ з навколишнього середовища, щоб точно компенсувати цю зміну. Це називається ізотермічним розширенням. В ізотермічному процесі внутрішня енергія залишається постійною, і ми можемо записати Перший Закон (Рівняння\(Ref{2-1}\)) як

\[0 = q + w\]

або

\[q = –w\]

Це ілюструє, що тепловий потік і виконана робота точно врівноважують один одного.

Оскільки ніяка теплоізоляція не ідеальна, по-справжньому адіабатичні процеси не відбуваються. Однак тепловий потік вимагає часу, тому стиснення або розширення, що відбувається швидше, ніж термічне врівноваження, можна вважати адіабатичним для практичних цілей. Якщо ви коли-небудь використовували ручний насос для накачування велосипедної шини, можливо, ви помітили, що дно стовбура насоса може досить нагрітися. Хоча невелика частина цього потепління може бути через тертя, це в основному результат роботи, яку ви (оточення) робите над системою (газом.)

Адіабатичне розширення і скорочення особливо важливі в розумінні поведінки атмосфери. Хоча ми зазвичай вважаємо атмосферу однорідною, це насправді не так, значною мірою через нерівномірне нагрівання та охолодження над локалізованими ділянками. Оскільки змішування та передача тепла між прилеглими ділянками повітря не відбувається швидко, багато поширених атмосферних явищ можна вважати принаймні квазіадіабатичними.

оборотні процеси

З Прикладу\(\PageIndex{1}\) ми бачимо, що коли газ розширюється в вакуум (\(P_{external} = 0\)виконана робота дорівнює нулю. Це мінімальна робота, яку може виконати газ; яку максимальну роботу може виконувати газ на навколишньому середовищі? Щоб відповісти на це, зверніть увагу, що більше роботи виконується, коли процес здійснюється в два етапи, ніж на одному етапі; простий розрахунок покаже, що ще більше роботи можна отримати, збільшивши кількість етапів - тобто, дозволяючи газу розширюватися проти ряду послідовно нижчих зовнішніх тисків. Для того щоб витягти з процесу максимально можливу роботу, розширення довелося б проводити в нескінченній послідовності нескінченно малих кроків. Кожен крок дає приріст роботи P Δ V, який може бути виражений як (RT/V) dV і інтегрований:

\[ \begin{align} w &= \int_{V_1}^{V_2} \dfrac{RT}{V} dv \\[4pt] &= RT \ln \dfrac{V_2}{V_1} \label{3-5} \end{align}\]

Хоча такий шлях (який відповідає тому, що називається оборотним процесом) не може бути реалізований на практиці, його можна наблизити так близько, як хочеться.

Незважаючи на те, що жоден реальний процес не може відбуватися оборотно (це займе нескінченно багато часу!) , оборотні процеси відіграють важливу роль у термодинаміці. Основна причина цього полягає в тому, що q _rev і w _rev - це функції стану, які важливі і легко обчислюються. Більш того, багато реальних процесів відбуваються досить поступово, щоб їх можна було розглядати як приблизно оборотні процеси для полегшення розрахунку.

Малюнок\(\PageIndex{1}\): Ці графіки ілюструють вплив різного ступеня оборотності на обсяг роботи, виконаної при розширенні газу, і роботу, яку необхідно виконати для того, щоб відновити його до початкового стану шляхом повторного стиснення. Робота, в кожному конкретному випадку, пропорційна затіненої площі на ділянці.

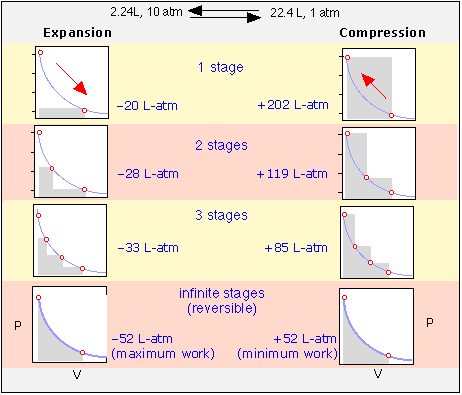
Кожен цикл розширення-стиснення залишає газ незмінним, але у всіх, крім того, що знаходиться в нижньому ряду, оточення назавжди змінюються, витративши більше роботи на стиснення газу, ніж виконувалося на ньому при розширенні газу. Тільки коли процеси виконуються в нескінченну кількість кроків, система та оточення будуть відновлені до своїх початкових станів - це сенс термодинамічної оборотності.

Тепло змінюється при постійному тиску: Ентальпія

Для хімічної реакції, яка не виконує жодної роботи над навколишнім середовищем, поглинене тепло таке ж, як зміна внутрішньої енергії: q = Δ U. Але багато хімічні процеси дійсно передбачають роботу в тому чи іншому вигляді:

• Якщо загальний обсяг продуктів реакції перевищує обсяг реагентів, то процес виконує роботу над оточенням в кількості P Δ V, в якому P - тиск, що чиниться оточенням (зазвичай атмосферою) на систему.
• Реакція, яка приводить електричний струм через зовнішній ланцюг, виконує електромонтажні роботи на навколишнє середовище.

Для ізотермічного процесу тисково-об'ємна робота впливає на теплоту q

Ми розглянемо тільки напірно-об'ємну роботу в цьому уроці. Якщо процес відбувається при постійному тиску, то робота дається P Δ V і зміна внутрішньої енергії буде

\[ΔU = q – PΔV \label{4-1}\]

Майте на увазі,\(q\) чому так важливо: потік тепла в систему або з неї безпосередньо вимірюється. Δ U, будучи «внутрішнім» для системи, безпосередньо не спостерігається. Таким чином, кількість тепла, яке проходить між системою і навколишнім середовищем, віддається

\[q = ΔU + PΔV \label{4-2}\]

Це означає, що якщо екзотермічна реакція супроводжується чистим збільшенням об'єму в умовах постійного тиску, деяке тепло, додаткове до Δ U, повинно бути поглинене, щоб забезпечити енергію, витрачену як роботу, виконану на навколишнє середовище, якщо температура повинна залишатися незмінною ( ізотермічний процес.)

Для більшості практичних цілей зміни обсягу системи істотні лише в тому випадку, якщо реакція супроводжується різницею молів газоподібних реагентів і продуктів.

Наприклад, в реакції H ₂ (g) + O ₂ (g) → ½H ₂ O (l) загальний об'єм системи зменшується від того, що відповідає 2 молям газоподібних реагентів до 0,5 моль рідкої води, яка займає всього 9 мл — обсяг настільки малий в порівняння з реагентами, якими можна нехтувати без суттєвої помилки. Отже, все, що нас дійсно хвилює, це різниця в кількості молів газу Δ n _g:

Δ n _г = (0 — 2) моль = —2 моль

Це відповідає чистому стисненню (негативному розширенню) системи, що означає, що оточення виконують роботу над системою.

Молярний об'єм ідеального газу при 25° С і 1 атм становить

(298/273) × (22,4 л моль ^—1) = 24,5 л моль ^—1

Пам'ятайте про знак умовності: потік тепла або виконання роботи, що постачає енергію, є позитивним; якщо він споживає енергію, то негативний. При цьому робота, що виконується оточенням, зменшує енергію оточення (w _surr < 0) і збільшує енергію системи (w _sys > 0).

і виконана робота (оточення на системі)

(1 атм) (—2 моль) (24,5 л моль ^—1) = —49,0 л атм.

Використовуючи коефіцієнт перетворення 1 Дж = 101,3 Дж, і маючи на увазі, що робота, що виконується на системі, постачає енергію в систему, робота, пов'язана виключно зі зміною обсягу системи, збільшує її енергію на

(101,3 Дж/л атм) (—49,0 л атм) = 4964 Дж = 4,06 кДж

Приклад\(\PageIndex{2}\)

Зазначену вище реакцію H ₂ (g) + ½ O ₂ (g) → H ₂ O (l) проводять при постійному тиску 1 атм і постійній температурі 25° С Яка кількість тепла q перетине межу системи (і в який бік?) Для цієї реакції зміна внутрішньої енергії дорівнює Δ U = —281,8 кДж/моль.

Рішення

281,8 кДж тепла. Роботи, що виконуються оточенням, подає в систему додаткову енергію P Δ V = 4,06 кДж. Загальна зміна енергії системи, таким чином

q = (—281,8 + 4,06) к Дж = —285,8 кДж

(Ур. 4.2 вище.) Щоб підтримувати постійну температуру 25°, еквівалентна кількість тепла повинна пройти від системи до навколишнього середовища.

Ця термінологія може бути дещо оманливою, якщо ви не маєте на увазі, що умови Δ P і Δ T стосуються відмінностей між початковим і кінцевим станами системи - тобто до і після реакції. За час протікання реакції температура суміші буде підвищуватися або падати, в залежності від того, чи є процес екзотермічним або ендотермічним. Але оскільки Δ T є функцією стану, її значення не залежить від того, що відбувається «між» початковим станом (реагентами) і кінцевим станом (продуктами). Те ж саме справедливо і з Δ V.

Ентальпія приховує роботу і зберігає її теж!

Оскільки більшість хімічних змін, з якими ми маємо справу, відбуваються при постійному тиску, було б нудно чітко мати справу з робочими деталями тиску та обсягу, які були описані вище. На щастя, хіміки знайшли спосіб обійти це; вони просто визначили нову державну функцію, яка включає і, таким чином, приховує в собі будь-які терміни, що стосуються випадкових видів робіт (P-V, електричні тощо). Оскільки і Δ P, і Δ V у\(\ref{4-2}\) рівнянні є функціями стану\(q_P\), то тепло, яке поглинається або виділяється, коли процес відбувається при постійному тиску, також має бути функцією стану і відоме як зміна ентальпії Δ H

\[ΔH ≡ q_P = ΔU + PΔV \label{4-3}\]

Оскільки більшість процесів, що відбуваються в лабораторії, на поверхні землі і в організмах роблять це під постійним тиском однієї атмосфери, Рівняння\(\ref{4-3}\) є формою Першого Закону, який представляє найбільший інтерес для більшості з нас більшу частину часу.

Приклад\(\PageIndex{3}\)

Хлористий водень легко розчиняється у воді, виділяючи 75,3 кДж/моль тепла в процесі. Якщо один моль HCl при тиску 298 К і 1 атм займає 24,5 літра, знайдіть Δ U для системи, коли один моль HCl розчиняється у воді в цих умовах.

Рішення

При цьому обсяг рідини залишається практично незмінним, тому Δ V = —24,5 л. Виконана робота

\[ \begin{align*} w &= –PΔV \\[4pt] &= –(1\; atm)(–24.5\; L) \\[4pt] &= 24.6 \;L-atm \end{align*}\]

(Робота позитивна, оскільки вона проводиться в системі, оскільки її обсяг зменшується через розчинення газу в набагато менший обсяг розчину.) Використовуючи коефіцієнт перетворення 1 L-атм = 101,33 J моль ^—1 та підставляючи в Рівняння\ ref {4-3} отримано

\[ \begin{align*} ΔU &= q +PΔV \\[4pt] = –(75,300\; J) + [101.33\; J/L-atm) (24.5\; L-atm)] \\[4pt] &= –72.82\; kJ \end{align*}\]

Іншими словами, якщо газоподібний HCl може розчинятися без зміни обсягу, тепло, що виділяється процесом (75,3 кДж), призведе до зменшення внутрішньої енергії системи на 75,3 кДж. Але зникнення газоподібної фази зменшує обсяг системи. Це еквівалентно стисненню системи тиском атмосфери, що виконує над нею роботу і споживає частину енергії, яка в іншому випадку була б звільнена, зменшуючи чисте значення Δ U до —72,82 к Дж.

Теплоємність

Для систем, в яких не відбувається зміни складу (хімічної реакції), справи йдуть ще простіше: до дуже хорошого наближення ентальпія залежить тільки від температури. Це означає, що температура такої системи може служити прямим заходом її ентальпії. Функціональне співвідношення між внутрішньою енергією і температурою задається теплоємністю, виміряної при постійному тиску:

\[ c_p =\dfrac{dH}{dT} \label{5-1}\]

(Або Δ H /Δ T за скінченною тривалістю) Аналогічна величина пов'язує теплоємність при постійному обсязі до внутрішньої енергії:

\[ c_v =\dfrac{dU}{dT} \label{5-2}\]

Чим більше теплоємність речовини, тим меншим буде вплив даного поглинання або втрати тепла на його температуру. Теплоємність може виражатися в джоулів або калоріях на моль на градус (молярна теплоємність), або в джоулі або калоріях на грам на градус; остання називається питомою теплоємністю або просто питомою теплоємністю. Різниця між\(c_p\) і\(c_v\) має важливе значення лише тоді, коли обсяг системи значно змінюється— тобто коли по обидва боки від хімічного рівняння з'являються різна кількість молів газів. Для реакцій беруть участь тільки рідини і тверді речовини,\(c_p\) і\(c_v\) для всіх практичних цілей ідентичні.