4.4: Урожайність реакції

Last updated
Save as PDF

Page ID: 22784

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть поняття теоретичного виходу і граничних реагентів/реагентів.
Вивести теоретичний вихід для реакції за заданих умов.
Обчисліть відсотковий вихід для реакції.

Відносні кількості реагентів і продуктів, представлених у збалансованому хімічному рівнянні, часто називають стехіометричними кількостями. Всі вправи попереднього модуля задіяні стехіометричні кількості реагентів. Наприклад, при розрахунку кількості продукту, що утворюється з заданої кількості реагенту, передбачалося, що будь-які інші необхідні реагенти були доступні в стехіометричних кількостях (або більших). У цьому модулі розглядаються більш реалістичні ситуації, при яких реагенти відсутні в стехіометричних кількостях.

обмежуючий реагент

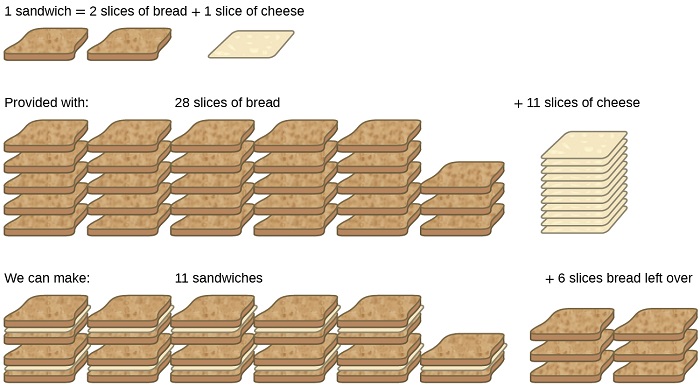
Розглянемо ще одну аналогію їжі, роблячи бутерброди з сиром на грилі (рис.\(\PageIndex{1}\)):

\[\text{1 slice of cheese} + \text{2 slices of bread} \rightarrow \text{1 sandwich} \label{4.5.A} \]

Стіхіометричні кількості інгредієнтів сендвіча для цього рецепта - це шматочки хліба та сиру в співвідношенні 2:1. За умови 28 скибочок хліба і 11 скибочок сиру, можна приготувати 11 бутербродів за наданою рецептурою, використовуючи весь наданий сир і залишивши шість скибочок хліба. При цьому сценарії кількість приготованих бутербродів була обмежена кількістю скибочок сиру, а хлібні скибочки були надані в надлишку.

Малюнок\(\PageIndex{1}\): Виготовлення сендвічів може проілюструвати поняття обмежуючих та надлишкових реагентів.

Розглянемо зараз це поняття щодо хімічного процесу, реакції водню з хлором з виходом хлористого водню:

\[\ce{H2}(g) + \ce{Cl2}(g)\rightarrow \ce{2HCl}(g) \nonumber \]

Збалансоване рівняння показує, що водень і хлор реагують у стехіометричному співвідношенні 1:1. Якщо ці реагенти надаються в будь-яких інших кількостях, один з реагентів майже завжди буде повністю споживатися, тим самим обмежуючи кількість продукту, який може генеруватися. Ця речовина є граничним реагентом, а інша речовина - надлишковим реагентом. Визначення граничних та надлишкових реагентів для даної ситуації вимагає обчислення молярних кількостей кожного наданого реагенту та порівняння їх зі стехіометричними кількостями, представленими у збалансованому хімічному рівнянні.

Наприклад, уявіть, що поєднують 6 родимок H ₂ і 4 родимки Cl ₂. Визначення граничного реагенту передбачає порівняння кількості продукту, очікуваного для повної реакції кожного реагенту. Кожна кількість реагенту використовується для окремого розрахунку кількості продукту, який буде утворюватися в стехіометрії реакції. Реагент, що дає меншу кількість продукту, є граничним реагентом.

Для прикладу в попередньому пункті повна реакція водню дасть

\[\mathrm{mol\: HCl\: produced=6\: mol\:H_2\times \dfrac{2\: mol\: HCl}{1\: mol\:H_2}=12\: mol\: HCl} \nonumber \]

Повна реакція наданого хлору буде виробляти

\[\mathrm{mol\: HCl\: produced=4\: mol\:Cl_2\times \dfrac{2\: mol\: HCl}{1\: mol\:Cl_2}=8\: mol\: HCl} \nonumber \]

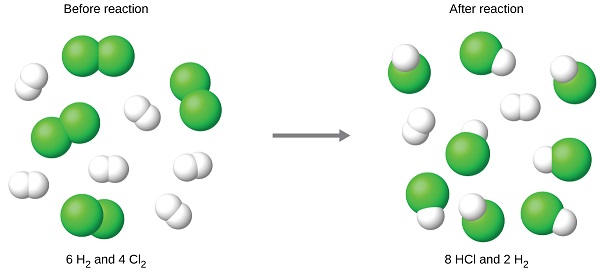
Хлор буде повністю споживатися після того, як буде вироблено 8 моль HCl. Оскільки було надано достатньо водню для отримання 12 молів HCl, після завершення цієї реакції залишиться нереагуючий водень. Тому хлор є граничним реагентом, а водень - надлишковим реагентом (рис.\(\PageIndex{2}\)). Для визначення кількості надлишку реагенту, яке залишилося, кількість водню, споживаного в реакції, можна відняти від вихідної кількості водню.

Кількість споживаного водню становить

\[\mathrm{mol\: H_2\: produced=8\: mol\:HCl\times \dfrac{1\: mol\: H_2}{2\: mol\:HCl}=4\: mol\: H_2} \nonumber \]

Відніміть витрачений водень з початкової кількості

\[\mathrm{mole\: of\: excess\:H_{2}=6\:mol\:H_{2}\:starting\:-\:4\:mol\:H_{2}\:consumed\:=\:2\:mol\:H_{2}\; excess} \nonumber \]

Малюнок\(\PageIndex{2}\): Коли H ₂ і Cl ₂ поєднуються в нестехіометричних кількостях, один з цих реагентів обмежить кількість HCl, який може бути вироблений. На цій ілюстрації показана реакція, в якій водень присутній в надлишку, а хлор є обмежуючим реагентом.

Приклад\(\PageIndex{1}\): Identifying the Limiting Reactant

Нітрид кремнію - це дуже тверда, стійка до високих температур кераміка, яка використовується як компонент лопатей турбін в реактивних двигунів. Його готують за наступним рівнянням:

\[\ce{3Si}(s)+\ce{2N2}(g)\rightarrow \ce{Si3N4}(s) \nonumber \]

Який граничний реагент, коли реагують 2,00 г Si і 1,50 г N ₂?

Рішення

Обчисліть надані молярні кількості реагентів, а потім порівняйте ці суми з збалансованим рівнянням, щоб визначити граничний реагент.

\[\mathrm{mol\: Si=2.00\:\cancel{g\: Si}\times \dfrac{1\: mol\: Si}{28.09\:\cancel{g\: Si}}=0.0712\: mol\: Si} \nonumber \]

\[\mathrm{mol\:N_2=1.50\:\cancel{g\:N_2}\times \dfrac{1\: mol\:N_2}{28.02\:\cancel{g\:N_2}}=0.0535\: mol\:N_2} \nonumber \]

Надане молярне співвідношення Si:N ₂ становить:

\[\mathrm{\dfrac{0.0712\: mol\: Si}{0.0535\: mol\:N_2}=\dfrac{1.33\: mol\: Si}{1\: mol\:N_2}} \nonumber \]

Стіхіометричне співвідношення SiN: ₂ становить:

\[\mathrm{\dfrac{3\: mol\: Si}{2\: mol\:N_2}=\dfrac{1.5\: mol\: Si}{1\: mol\:N_2}} \nonumber \]

Порівняння цих співвідношень показує, що Si забезпечується в меншій, ніж стехіометричної кількості, як і граничний реагент.

Крім того, обчислити кількість продукту, очікуваного для повної реакції кожного з наданих реагентів. 0.0712 молі кремнію дадуть

\[\mathrm{mol\:Si_3N_4\:produced=0.0712\: mol\: Si\times \dfrac{1\:mol\:Si_3N_4}{3\: mol\: Si}=0.0237\: mol\:Si_3N_4} \nonumber \]

тоді як 0,0535 молів азоту вироблятиме

\[\mathrm{mol\:Si_3N_4\:produced=0.0535\: mol\:N_2\times \dfrac{1\: mol\:Si_3N_4}{2\: mol\:N_2}=0.0268\: mol\:Si_3N_4} \nonumber \]

Оскільки кремній дає меншу кількість продукту, він є граничним реагентом.

Вправа\(\PageIndex{1}\)

Який граничний реагент, коли 5,00 г Н ₂ і 10,0 г O ₂ реагують і утворюють воду?

Відповідь: О ₂

Відсоток прибутковості

Кількість продукту, яке може бути отримано реакцією в заданих умовах, розраховане за стехіометрією відповідного збалансованого хімічного рівняння, називається теоретичним виходом реакції. На практиці кількість отриманого продукту називається фактичним виходом, і воно часто менше теоретичного виходу з ряду причин. Деякі реакції за своєю суттю неефективні, супроводжуючись побічними реакціями, які генерують інші продукти. Інші за своєю природою неповні (розглянемо часткові реакції слабких кислот і підстав, розглянуті раніше в цьому тексті). Деякі продукти важко зібрати без деяких втрат, і тому менш досконале відновлення знизить фактичну врожайність. Ступінь, в якій досягається теоретичний вихід реакції, зазвичай виражається як її відсотковий вихід:

\[\mathrm{percent\: yield=\dfrac{actual\: yield}{theoretical\: yield}\times 100\%} \nonumber \]

Фактичний і теоретичний вихід може виражатися як маси або молярні суми (або будь-яке інше відповідне властивість; наприклад, обсяг, якщо продукт є газом). Поки обидві врожайності виражаються з використанням однакових одиниць, ці одиниці скасовуватимуться, коли обчислюється відсоткова прибутковість.

Приклад\(\PageIndex{2}\): Calculation of Percent Yield

При реакції 1,274 г мідного купоросу з надлишком металу цинку отримано 0,392 г мідного металу за рівнянням:

\[\ce{CuSO4}(aq)+\ce{Zn}(s)\rightarrow \ce{Cu}(s)+\ce{ZnSO4}(aq) \nonumber \]

Що таке відсоткова прибутковість?

Рішення

Надана інформація ідентифікує мідний купорос як граничний реагент, і тому теоретичний вихід виявляється підходом, проілюстрованим у попередньому модулі, як показано тут:

\[\mathrm{1.274\:\cancel{g\:Cu_SO_4}\times \dfrac{1\:\cancel{mol\:CuSO_4}}{159.62\:\cancel{g\:CuSO_4}}\times \dfrac{1\:\cancel{mol\: Cu}}{1\:\cancel{mol\:CuSO_4}}\times \dfrac{63.55\:g\: Cu}{1\:\cancel{mol\: Cu}}=0.5072\: g\: Cu} \nonumber \]

Використовуючи цю теоретичну прибутковість і надане значення для фактичної прибутковості, відсоток прибутковості розраховується як

\[\mathrm{percent\: yield=\left(\dfrac{actual\: yield}{theoretical\: yield}\right)\times 100} \nonumber \]

\ [\ почати {вирівнювати*}
\ математика {відсоток\: вихід} &=\ математика {\ лівий (\ dfrac {0.392\: g\: Cu} {0.5072\: g\: Cu}\ праворуч)\ раз 100}\
&=77.3\%
\ end {вирівнювати*}\ nonumber\]

Вправа\(\PageIndex{2}\)

Який відсоток виходу реакції, яка виробляє 12,5 г газу фреон CF _{2 Cl ₂} з 32,9 г cCl ₄ і надлишок HF?

\[\ce{CCl4 + 2HF \rightarrow CF2Cl2 + 2HCl} \nonumber \]

Відповідь: 48,3%

Зелена хімія та атомна економіка

Цілеспрямоване проектування хімічних продуктів і процесів, що мінімізують використання екологічно небезпечних речовин і утворення відходів, відомо як зелена хімія. Зелена хімія - це філософський підхід, який застосовується до багатьох областей науки і техніки, і її практика узагальнена керівними принципами, відомими як «Дванадцять принципів зеленої хімії». Один з 12 принципів спрямований саме на максимальну ефективність процесів синтезу хімічних продуктів. Атомна економія процесу є мірою цієї ефективності, визначеною як відсоток за масою кінцевого продукту синтезу щодо мас усіх використовуваних реагентів:

\[\mathrm{atom\: economy=\dfrac{mass\: of\: product}{mass\: of\: reactants}\times 100\%} \nonumber \]

Хоча визначення атомної економіки на перший погляд здається дуже схожим на визначення відсоткового виходу, майте на увазі, що ця властивість являє собою різницю в теоретичній ефективності різних хімічних процесів. З іншого боку, відсоток виходу даного хімічного процесу оцінює ефективність процесу, порівнюючи вихід фактично отриманого продукту з максимальним виходом, прогнозованим стехіометрією.

Синтез загальних безрецептурних знеболюючих препаратів, ібупрофену, красиво ілюструє успіх зеленого хімії підходу (рис.\(\PageIndex{3}\)). Вперше продавався на початку 1960-х, ібупрофен вироблявся з використанням шестиступінчастого синтезу, який вимагав 514 г реагентів для генерації кожного моля (206 г) ібупрофену, атомна економіка 40%. У 1990-х роках компанія BHC (нині корпорація BHC) розробила альтернативний процес, який вимагає всього трьох кроків і має атомну економіку ~ 80%, майже вдвічі більше, ніж початковий процес. Процес BHC генерує значно менше хімічних відходів; використовує менш небезпечні та переробні матеріали; і забезпечує значну економію коштів виробнику (а згодом і споживачеві). На знак визнання позитивного впливу процесу BHC на навколишнє середовище компанія отримала нагороду «Екологічні синтетичні шляхи» Агентства з охорони навколишнього середовища в 1997 році.

Малюнок\(\PageIndex{3}\): (а) Ібупрофен - популярний безрецептурний знеболюючий препарат, який зазвичай продається у вигляді таблеток 200 мг. (б) Процес BHC для синтезу ібупрофену вимагає всього трьох етапів і демонструє вражаючу економію атомів. (Кредит: модифікація роботи Дерріка Коетзі)

Резюме

Коли реакції проводяться з використанням менш стехіометричних кількостей реагентів, кількість виробленого продукту буде визначатися граничним реагентом. Кількість продукту, що утворюється в результаті хімічної реакції, є його фактичним виходом. Цей вихід часто менше кількості продукту, передбаченого стехіометрією збалансованого хімічного рівняння, що представляє реакцію (її теоретичний вихід). Ступінь, в якій реакція генерує теоретичну кількість продукту, виражається як його відсотковий вихід.

Ключові рівняння

\(\mathrm{percent\: yield=\left(\dfrac{actual\: yield}{theoretical\: yield}\right)\times 100}\)

Глосарій

фактична прибутковість: кількість продукту, що утворюється в реакції

надлишок реагенту: реагент присутній в кількості, більшій, ніж потрібно стехіометрії реакції

обмежуючий реагент: реагент присутній в кількості, меншій, ніж потрібно стехіометрії реакції, тим самим обмежуючи кількість виробленого продукту

відсоток прибутковості: міра ефективності реакції, виражена у відсотках від теоретичного виходу

теоретична прибутковість: кількість продукту, який може бути отриманий із заданої кількості реагенту (ів) відповідно до стехіометрії реакції