11.5: Розрахунки рівноваги
- Page ID
- 19113
П'ять прикладів, представлених вище, були ретельно відібрані, щоб охопити діапазон типів проблем, які студенти, які навчаються на курсах хімії першого курсу коледжу, як очікується, зможуть мати справу з. Якщо ви в змозі відтворити ці рішення самостійно, вам слід бути добре підготовленим на цю тему.
- Першим кроком у вирішенні всіх, крім найпростіших задач рівноваги, є накреслення таблиці, яка показує для кожного компонента початкову концентрацію або тиск, зміну цієї величини (наприклад, +2 х) і значення рівноваги (наприклад,. 0036 + 2 х). При цьому послідовність розрахунків, необхідна для того, щоб дістатися до відповіді, зазвичай стає очевидною.
- Розрахунки рівноваги часто включають квадратні або вищі рівняння порядку. Оскільки концентрації, тиск і константи рівноваги рідко відомі з точністю більше, ніж кілька значущих цифр, немає необхідності шукати точні рішення. Ітераційні наближення (як у прикладі\(\PageIndex{3}\)) або використання графічного калькулятора (приклад\(\PageIndex{4}\)) адекватні та зручні.
- Рівноваги фазового розподілу відіграють важливу роль у процесах хімічного поділу як в лабораторних, так і в промислових масштабах. Вони також беруть участь в переміщенні хімічних речовин між різними частинами навколишнього середовища, і в біоконцентруванні забруднюючих речовин в харчовому ланцюзі.
На цій сторінці представлені приклади, які охоплюють більшість видів проблем рівноваги, з якими ви, ймовірно, зіткнетеся на першому курсі університету. Читання цієї сторінки не навчить вас працювати з проблемами рівноваги! Єдиний, хто може навчити вас тлумачити, розуміти і вирішувати проблеми - це ви самі. Тож не просто «читайте» це і думайте, що ви закінчили. Знайти і вирішувати подібні проблеми потрібно самостійно. Перегляньте проблеми в домашньому завданні або в кінці відповідної глави підручника, і подивіться, як вони вписуються в загальні типи, описані нижче. Коли ви зможете їх вирішити, не дивлячись на приклади нижче, ви будете добре на своєму шляху!
Обчислення констант рівноваги
Зрозуміло, що якщо концентрації або тиск всіх компонентів реакції відомі, то значення\(K\) можна знайти шляхом простої підміни. Однак дотримання індивідуальних концентрацій або парціального тиску може бути не завжди практичним. Якщо один з компонентів забарвлений, то ступінь, в якій він поглинає світло відповідної довжини хвилі, може служити показником його концентрації. Вимірювання тиску зазвичай здатні вимірювати лише загальний тиск газоподібної суміші, тому, якщо в рівноважній суміші присутні два або більше газоподібних продуктів, парціальний тиск одного, можливо, доведеться зробити висновок з тиску іншого, беручи до уваги стехіометрію реакції.
В експерименті, проведеному Тейлором і Крістом (J.Am. Хім. Soc. 1941:1377), було виявлено, що йодид водню 22,3% дисоційований при 730.8 К. Розрахувати\(K_c\) для
\[\ce{ 2 HI(g) <=> H2(g) + I2} \nonumber \]
Рішення
Явних молярних концентрацій не наведено, але ми знаємо, що для кожної\(n\)\(0.223n\) родимки\(\ce{HI}\), утворюються родимки кожного продукту і\((1–0.223)n = 0.777n\) родимки\(\ce{HI}\) залишків. Для простоти припустимо, що\(n=1\) і що реакція проводиться в посудині 1,00-л, так що ми можемо підставити необхідні терміни концентрації безпосередньо в рівноважний вираз для\(K_c\).
\[\begin{align*} K_c &= \dfrac{[\ce{H2}][\ce{I2}]}{[\ce{HI}]^2} \\[4pt] &= \dfrac{(0.223)(0.223)}{(0.777)^2} \\[4pt] &= 0.082 \end{align*}\]
Звичайний білий фосфор\(\ce{P4}\), утворює пар, який дисоціює на двоатомні молекули при високих температурах:
\[\ce{P4(g) <=> 2 P2(g)} \nonumber\]
У зразку білого фосфору при нагріванні до 1000°С утворюється пар, що має загальний тиск 0,20 атм і щільність 0,152 г л —1. Використовуйте цю інформацію для оцінки константи рівноваги\(K_p\) для цієї реакції.
Рішення
Перш ніж турбуватися про те, до чого має відношення щільність газової суміші\(K_p\), почніть звичайним способом з викладання інформації, необхідної для вираження\(K_p\) в терміні невідомого\(x\)
| Стіл ICE | \(P_{4(g)}\) | \(P_{2(g)}\) | коментар |
|---|---|---|---|
| I початковий (родимки) | \ (P_ {4 (g)}\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; "> 1 | \ (P_ {2 (g)}\)» style="вертикальне вирівнювання: середина; "> 0 | Так як\(K\) не залежить від кількості родимок, припустимо найпростіший початковий випадок. |
| Зміна C (родимки) | \ (P_ {4 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(-x\) | \ (P_ {2 (g)}\)» style="вертикальне вирівнювання: середина; ">\(2x\) | х - частка P 4, яка дисоціює. |
| Е рівновага (родимки) | \ (P_ {4 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(1-x\) | \ (P_ {2 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(2x\) | Знаменником є загальна кількість родимок: |
| Моль Фракція | \ (P_ {4 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(\chi_{P_4}=\dfrac{1-x}{1+x}\) | \ (P_ {2 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(\chi_{P_2}=\dfrac{2x}{1+x}\) | Знаменником є загальна кількість родимок: |
| Рівновага (тиск) |
\ (P_ {4 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(p_{P_4} = \chi_{P_4} 0.2 = \left( \dfrac{1-x}{1+x}\right) 0.2 \) | \ (P_ {2 (g)}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">\(p_{P_2} = \chi_{P_2} 0.2 = \left( \dfrac{2x}{1+x}\right) 0.2 \) | Парціальний тиск - моль частка, що перевищує загальний тиск. |
Парціальні тиски в нижньому ряду були виявлені шляхом множення мольної частки кожного газу на загальний тиск:
\[P_i = \chi_i P_{tot} \nonumber\]
з терміном в знаменнику кожного мольного дробу - це загальна кількість молів газу, присутніх при рівновазі:
\[P_{tot} = 1-x + 2x = 1+x \nonumber\]
Висловлюючи константу рівноваги з точки зору\(x\) дає
\[ \begin{align*} K_p &= \dfrac{p^2_{P_2}}{p_{P_4}} \\[4pt] &= \dfrac{\left(\dfrac{2x}{1+x}\right)^2 0.2^2} {\left(\dfrac{1-x}{1+x}\right) 0.2} \\[4pt] &= \left(\dfrac{4x^2}{(1-x)(1+x)}\right) 0.2 \\[4pt] &= \left(\dfrac{4x^2}{1+x^2}\right) 0.2 \end{align*}\]
Тепер нам потрібно знайти частку\(x\) дисоціації\(P_4\), і в цей момент ми сподіваємося, що ви пам'ятаєте ті газові закони, які вам сказали, що вам знадобиться пізніше в курсі! Щільність газу прямо пропорційна його молекулярній масі, тому потрібно розраховувати щільності чистих\(P_4\) і чистих\(P_2\) парів в умовах експерименту. Одна з цих щільностей буде більшою за 0.152 gL —1, а інша буде меншою; все, що вам потрібно зробити, це знайти, де виміряна щільність потрапляє між двома межами, і у вас буде частка дисоціації.
Молекулярна маса фосфору становить 31,97, що дає молярну масу 127,9 г для\(\ce{P4}\). Цю масу потрібно розділити на об'єм, щоб знайти щільність; припускаючи ідеальну поведінку газу, обсяг 127,9 г (1 моль)\(\ce{P4}\) задається RT/P, який працює до 522 л (пам'ятайте, що тут використовується абсолютна температура.) Щільність чистої\(\ce{P4}\) пари в умовах експерименту
\[\rho = \dfrac{m}{V} = (128\; g \;mol^{–1}) \times x = (522\; L mol^{–1}) = 0.245\; g\; L^{–1} \nonumber\]
Щільність чистого\(P_2\) становила б половину цієї, або 0,122 г L —1. Різниця між цими двома граничними щільностями становить 0,123 г L —1, а різниця між щільністю чистої\(\ce{P4}\) та щільністю рівноважної суміші становить (0,245-0,152) г L —1 або 0,093 г L —1. Отже, співвідношення 0,093/0,123 = 0,76 є часткою\(\ce{P4}\), що залишається, і його дробова дисоціація становить (1 - 0,76) = 0,24. Підставляючи в вираз рівноваги вище дає\(K_p = 1.2\).
Вирішити приклад,\(\PageIndex{2}\) використовуючи інший набір початкових умов, щоб продемонструвати, що початкові умови дійсно не впливають на визначення стану рівноваги і\(K_p\).
Розрахунок концентрацій рівноваги
Це, безумовно, найпоширеніший вид проблеми рівноваги, з якою ви зіткнетеся: починаючи з довільної кількості родимок кожного компонента, скільки родимок кожного буде присутнім, коли система прийде до рівноваги? Основне джерело плутанини і помилки для початківців стосується необхідності визначення значень декількох невідомих (концентрації або тиску для кожної складової) з одного рівняння, виразу рівноваги. Ключем до цього є використання стехіометричних взаємозв'язків між різними компонентами, які зазвичай дозволяють висловити рівноважний склад з точки зору однієї змінної. Найпростіший і безпомилковий спосіб зробити це - прийняти системний підхід, в якому ви створюєте та заповнюєте невелику таблицю, як показано в наступному прикладі проблеми. Потім ви підставляєте значення рівноваги в вираз постійної рівноваги і вирішуєте його для невідомого.
Це дуже часто включає в себе рішення квадратичного або вищого порядку рівняння. Квадратику, звичайно, можна вирішити за допомогою знайомої квадратичної формули, але часто простіше використовувати алгебраїчне або графічне наближення, а для рівнянь вищого порядку це єдиний практичний підхід. Практично ніколи не потрібно отримувати точну відповідь, оскільки константи рівноваги, з яких ви починаєте, рідко відомі все, що точно так чи інакше.
Фосген (\(\ce{COCl2}\)) - отруйний газ, який дисоціює при високій температурі на два інших отруйних гази, чадний газ і хлор. Константа рівноваги K p = 0,0041 при 600°С. Знайти рівноважний склад системи після 0,124 атм\(\ce{COCl2}\) дозволяє досягти рівноваги при цій температурі.
Рішення
Для початку нам потрібна збалансована хімічна реакція.
\[\ce{COCl_2 <=> CO(g) + Cl2(g)} \nonumber\]
Почніть зі складання таблиці із зазначенням взаємозв'язків між компонентами:
| Стіл ICE | \(COCl_2\) | \(CO_{(g)}\) | \(Cl_{2(g)}\) |
|---|---|---|---|
| I початковий (тиск) | \ (CoCl_2\)» style="вирівнювання тексту: центр; "> 0.124 атм | \ (CO_ {(g)}\)» style="вирівнювання тексту: центр; "> 0 | \ (Cl_ {2 (g)}\)» style="вирівнювання тексту: центр; "> 0 |
| Зміна C (тиск) | \ (CoCl_2\)» style="вирівнювання тексту: центр; ">-x | \ (CO_ {(g)}\)» style="вирівнювання тексту: центр; ">+x | \ (Cl_ {2 (g)}\)» style="вирівнювання тексту: центр; ">+x |
| Е рівновага (тиск) | \ (CoCl_2\)» style="вирівнювання тексту: центр; "> 0.124 — x | \ (CO_ {(g)}\)» style="вирівнювання тексту: центр; ">+x | \ (Cl_ {2 (g)}\)» style="вирівнювання тексту: центр; ">+x |
Заміна рівноважних тисків на вираз рівноваги дає
\[ \dfrac{x^2}{0.124 - x} = 0.0041 \nonumber\]
Цей вираз можна переставити в стандартну многочленную форму
\[x^2 +0.0041 x – 0.00054 = 0 \nonumber\]
і вирішується квадратичною формулою, але ми просто отримаємо приблизне рішення шляхом ітерації. Оскільки постійна рівноваги мала, ми знаємо, що х буде досить малим порівняно з 0,124, тому вищевказане відношення може бути наближено
\[ \dfrac{x^2}{0.124 - x} \approx \dfrac{x^2}{0.124}= 0.0041 \nonumber\]
що дає х = 0,0225. Щоб побачити, наскільки це добре, підставляємо це значення x у знаменник вихідного рівняння і вирішуємо ще раз:
\[ \dfrac{x^2}{0.124 - 0.0225} = \dfrac{x^2}{0.102}= 0.0041 \nonumber\]
Цього разу рішення для\(x\) дає 0.0204. Перебираючи ще раз, отримуємо
\[ \dfrac{x^2}{0.124 - 0.0204} = \dfrac{x^2}{0.104}= 0.0041 \nonumber\]
і x = 0,0206, який досить близький до попереднього, щоб вважатися кінцевим результатом. Кінцеві парціальні тиски тоді становлять 0.104 атм для CoCl 2, і 0.0206 атм кожен для CO і Cl 2.
Коментар: Використання квадратичної формули для пошуку точного розв'язку дає два корені —0.0247 (які ми ігноруємо) і 0.0206, які показують, що наше наближення є досить хорошим.
Газофазова дисоціація пентахлориду фосфору до трихлориду має\(K_p = 3.60\) при 540°С:
\[\ce{PCl5(g) <=> PCl3(g) + Cl2(g)} \nonumber\]
Яким буде парціальний тиск всіх трьох складових, якщо об'єднати\(\ce{PCl5}\) і довести до рівноваги 0,200 моль і 3,00 моль при цій температурі і при загальному тиску 1,00 атм?\(\ce{PCl3}\)
Рішення
Як завжди, створіть таблицю, що показує те, що ви знаєте (перші два рядки), а потім виражаючи рівноважні величини:
| Стіл ICE | \(\ce{PC5(g)}\) | \(\ce{PCl3(g)}\) | \(\ce{Cl2(g)}\) |
|---|---|---|---|
| Початкова (родимки) | \ (\ ce {PC5 (g)}\)» style="вирівнювання тексту: центр; "> 0.200 | \ (\ ce {pCl3 (g)}\)» style="вирівнювання тексту: центр; ">3.00 | \ (\ ce {Cl2 (g)}\)» style="вирівнювання тексту: центр; "> 0 |
| Зміна (родимки) | \ (\ ce {PC5 (g)}\)» style="вирівнювання тексту: центр; ">—x | \ (\ ce {pCl3 (g)}\)» style="вирівнювання тексту: центр; ">+x | \ (\ ce {Cl2 (g)}\)» style="вирівнювання тексту: центр; ">+x |
| Рівновага (родимки) | \ (\ ce {PC5 (g)}\)» style="вирівнювання тексту: центр; "> 0.200 — x | \ (\ ce {pCl3 (g)}\)» style="вирівнювання тексту: центр; ">3.00 + x | \ (\ ce {Cl2 (g)}\)» style="вирівнювання тексту: центр; "> x |
| Рівновага (парціальний тиск) | \ (\ ce {PC5 (g)}\)» style="вирівнювання тексту: центр; ">\(\dfrac{2.00 - x }{ 3.20 + x}\) | \ (\ ce {pCl3 (g)}\)» style="вирівнювання тексту: центр; ">\(\dfrac{3.00 + x }{ 3.20 + x}\) | \ (\ ce {Cl2 (g)}\)» style="вирівнювання тексту: центр; ">\(\dfrac{ x }{ 3.20 + x}\) |
Парціальні тиски в нижньому ряду були виявлені шляхом множення мольної частки кожного газу на загальний тиск:
\[P_i = \chi_i P_{tot} \nonumber\]
з терміном в знаменнику кожного мольного дробу - це загальна кількість молів газу, присутніх при рівновазі:
\[P_{tot} = (0.200 – x) + (3.00 + x) + x = 3.20 + x \nonumber\]
Підставляючи рівноважні парціальні тиски в вираз рівноваги, ми маємо
\[ \dfrac{ (3.00 +x)(x)}{(0.200 -x)(3.20 +x)} = 3.60 \nonumber\]
форма многочлена якого
\[4.60x^2 + 13.80x – 2.304 = 0. \nonumber\]
Ви можете використовувати квадратичне питання для вирішення цього питання або ви можете зробити це графічно (більш корисно для рівнянь вищого порядку). Побудова цього на графічному калькуляторі дає\(x = 0.159\) позитивний корінь:
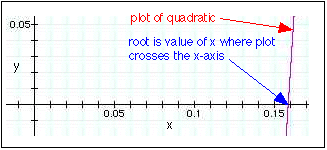
Підстановка цього кореня в вирази для рівноважного парціального тиску в таблиці дає наступні значення:
- \(P_{\ce{PCl5}}\)= 0,012 атм,
- \(P_{\ce{PCl3}}\)= 0,94 атм,
- \(P_{\ce{Cl2}}\)= 0,047 атм.
Вплив розведення на рівновагу
У розділі, який ввів принцип Ле Шательє, було згадано, що розведення слабкої кислоти, такої як оцтова кислота\(\ce{CH3COOH}\) («\(\ce{HAc}\)»), змістить рівновагу дисоціації вправо:
\[\ce{HAc + H_2O \rightleftharpoons H_3O^{+} + Ac^{–}} \nonumber\]
Таким чином\(0.10\,M\) розчин оцтової кислоти іонізується 1,3%, в той час як в 0,01 М розчині 4,3%\(\ce{HAc}\) молекул буде дисоційовано. Це пояснюється тим, що коли розчин стає більш розбавленим, продукт [H 3 O +] [Ac —] зменшується швидше, ніж\(\ce{[HAc]}\) термін. У той же час концентрація\(\ce{H2O}\) стає більшою, але оскільки вона настільки велика для початку (близько 55,5 М), будь-який ефект, який це може мати, незначний, тому жоден\(\ce{[H2O]}\) термін не з'являється у виразі рівноваги.
Для такої реакції, як
\[\ce{CH_3COOH (l) + C_2H_5OH (l) \rightleftharpoons CH_3COOC_2H_5 (l) + H_2O (l) }\]
(При якому концентрація води дійсно змінюється), розведення не вплине на рівновагу; ситуація аналогічна тому, як залежність тиску газофазної реакції залежить від кількості молів газових компонентів по обидва боки рівняння (тобто\(\Delta n_g\)).
Біохімічне утворення дисахаридного (подвійного) цукру з двох моносахаридів є прикладом реакції
\[\text{fructose} (aq) + \text{glucose-6-phosphate} (aq) → \text{sucrose-6-phosphate} (aq) + \ce{H2O} (l)\]
(Сахароза - звичайний столовий цукор.) До якого обсягу слід розводити розчин, що містить 0,050 моль кожного моносахариду, щоб довести 5% перетворення в фосфат сахарози? Константа рівноваги для цієї реакції знаходиться\(K_{c} = 7.1 \times 10^{-6}\) при кімнатній температурі.
Рішення
Початкове і кінцеве числа молів в цьому рівнянні такі:
| Стіл ICE | фруктоза (1\(\text{fruc}\)) | Глюкоза-6-Р (\(\text{gluc6P}\)) | Сахароза-6-П (\(\text{suc6P}\)) | вода\( \ce{H2O}\)) |
|---|---|---|---|---|
| I початковий (родимки) | \ (\ text {fruc}\))» style="вертикальне вирівнювання: середина; "> 0,05 | \ (\ text {Gluc6p}\))» style="вертикальне вирівнювання: середина; "> 0,05 | \ (\ text {SUC6P}\))» style="вертикальне вирівнювання: середина; "> 0 | \ (\ ce {H2O}\))» style="вертикальне вирівнювання: середина; ">- |
| Зміна C (родимки) | \ (\ text {fruc}\))» style="вертикальне вирівнювання: середина; ">-x | \ (\ text {Gluc6p}\))» style="вертикальне вирівнювання: середина; ">-x | \ (\ text {SUC6P}\))» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">+x | \ (\ ce {H2O}\))» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">- |
| Е рівновага (родимки) | \ (\ text {fruc}\))» style="вертикальне вирівнювання: середина; "> 0,05-x | \ (\ text {Gluc6p}\))» style="вертикальне вирівнювання: середина; "> 0,05-x | \ (\ text {SUC6P}\))» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">+x | \ (\ ce {H2O}\))» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; ">- |
Що таке цінність\(x\)? Тобто коли протікала 5% реакції або коли витрачається 5% фруктози (або глюкозо-6-Р):
\[\dfrac{x}{0.05} = 0.05 \nonumber\]
так\(x = 0.0025 \nonumber\). Тоді врівноважені концентрації
- \([\text{suc6P}]_{equil} = \dfrac{0.0025}{V}\)
- \([\text{fruc}]_{equil} = \dfrac{0.0475}{V}\)
- \([\text{glu6P}]_{equil} = \dfrac{0.0475}{V}\)
Підставляючи в значення в для виразу\(K_c\) (в якому обсяг рішення невідомий), ми маємо
\[\begin{align*} K_{c} &= \dfrac{[\text{suc6P}]_{equil} }{[\text{fruc}]_{equil} [\text{gluc6P}]_{equil} } \\[4pt] &= \dfrac{\left(\dfrac{0.0025}{V}\right)}{\left(\dfrac{0.0475}{V}\right)^2} = 7.1 \times 10^{-6} \end{align*}\]
\[V = (7.1 \times 10^{-6}) \dfrac{(0.0475)^2}{0.0025} \nonumber\]
Рішення для\(V\) дає кінцевий обсяг розчину\(6.4 \times 10^{-4}\,L\) або\(640 \mu L\). Чому такий маленький? Реакція не сприятлива, і щоб висунути її вперед, потрібні великі концентрації реагентів (принцип Ле Шательє в дії).
