Skip to main content
LibreTexts - Ukrayinska

Кінетико-молекулярна теорія

  1. Last updated
  2. Save as PDF
  • Page ID
    24553

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Навички для розвитку

    • Визначте кінетико-молекулярну теорію та її зв'язок з рівнянням ідеального газу

    Закон Бойла був опублікований близько 1660 року. У 1718 році математик на ім'я Бернуллі запропонував пояснення закону Бойля. Хоча це було майже за сто років до атомної теорії Дальтона, атомістичні теорії (також іноді називаються «корпускулярними теоріями») були довгим часом. Сам Бойл зробив деякі аргументи, подібні до Далтона, які він запозичив у Сеннерта. Бернуллі припустив, що газ зроблений з безлічі дрібних частинок, які швидко рухаються. Вони рухаються прямо, поки не натикаються на іншу частинку або стіну, потім відскакують відповідно до збереження імпульсу. Тиск виникає від удару, коли ці частинки натикаються на стінки.

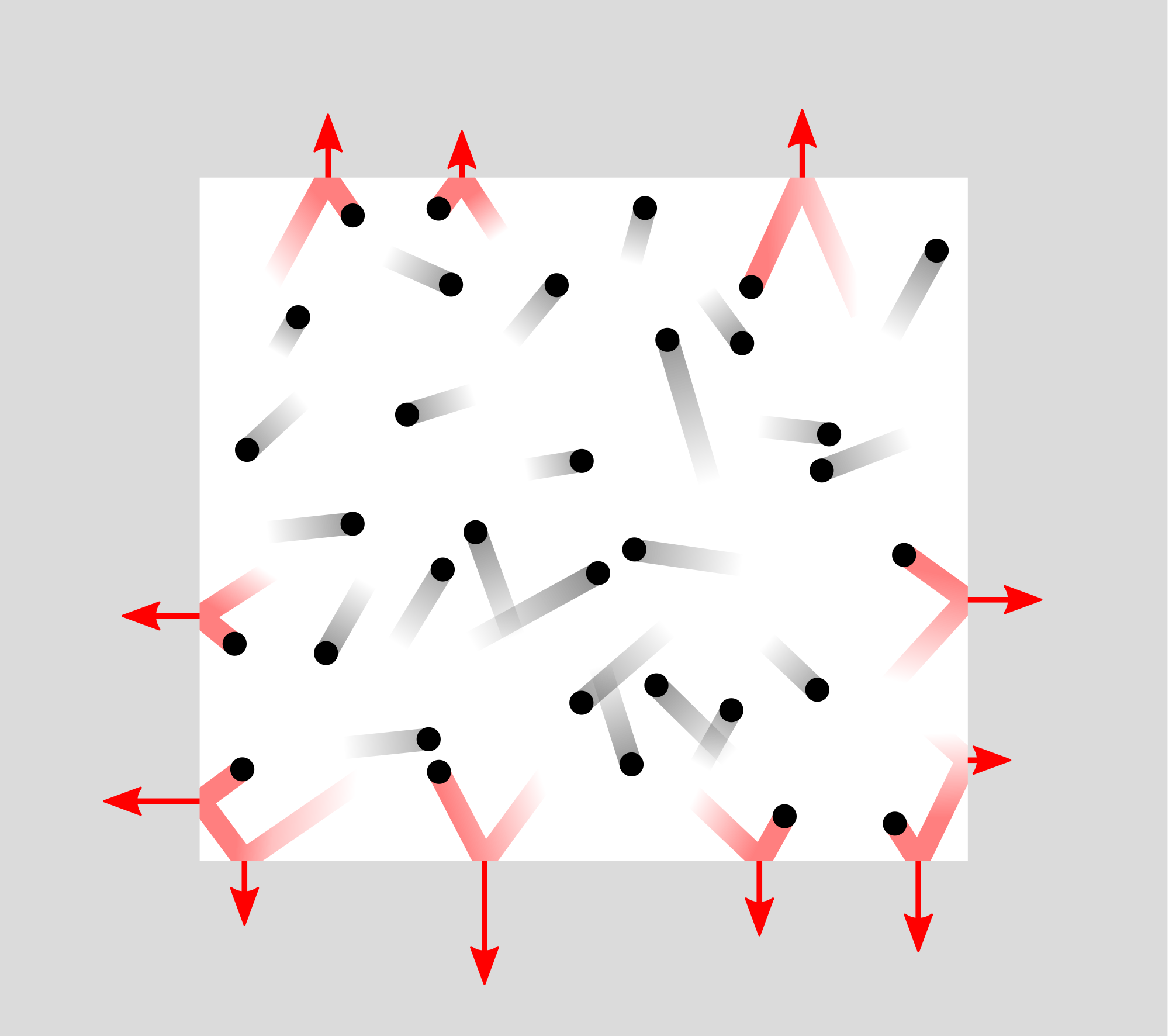
    Ілюстрація пояснення Бернуллі тиску газу.

    Як залежить тиск від обсягу? Бернуллі дає таке пояснення. Якщо ми стискаємо газ, частинки будуть частіше натикатися на стінки. Відбувається це з 2 причин: по-перше, в шарі поруч зі стіною залишається більше частинок, де вони можуть її натикати. По-друге, частинки, що віддаляються від стіни, швидше за все, зіткнуться з іншою частинкою, змінюють напрямок і знову натикаються на стіну. Уявімо, що у нас є кубічна ємність, з кожної сторони довжина s Якщо обсяг зменшується з 1 до s 3, то кількість частинок в шарі поруч зі стінкою збільшується на s 2 /1. Також кількість зіткнень між частинками стінового шару і стіною збільшується на с/1. Поєднуючи їх, кількість зіткнень збільшується на s 3 при зменшенні гучності на 1/с 3. Тиск - це кількість ударів, помножене на імпульс частинок, mv, де m - маса частинки, а v - середня швидкість. При обчисленні середньої зміни імпульсу від кожного зіткнення і середньої кількості зіткнень на площу стіни, результатом є P = nmv 2 /3V, де n - кількість частинок, а V - об'єм. Ви можете бачити, що це відповідає закону Бойла: PV = nmv 2/3 = постійна. Пізніше було показано, що кінетична енергія mv 2 пропорційна температурі: kT = mv 2. Це ідеальне рівняння газу.

    Як швидко рухаються частинки газу? Оскільки середня кінетична енергія пропорційна температурі, важчі гази рухаються повільніше, ніж легкі гази при тій же температурі. Буде великий діапазон швидкостей для різних молекул, тому що вони змінюють швидкість, коли вони відштовхуються один від одного. Для N 2 при 0° C діапазон може становити 0-1300 м/с, із середньою швидкістю близько 500 м/с, коли температура стає більшою, діапазон стає більшим, як і середня швидкість. Так що частинки зазвичай рухаються дуже швидко! Як далеко вони йдуть між зіткненнями? Це залежить від умов, але середня відстань між зіткненнями може становити 10 - 7 м, так далеко!

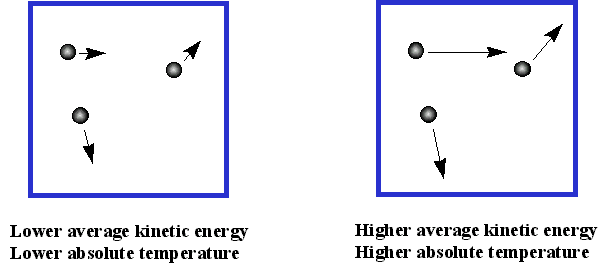
    Таким чином, ми уявляємо собі газ стільки дрібних частинок, які ідеально пружно відштовхуються один від одного (зі збереженням імпульсу). Вони поводяться як жорсткі маленькі кульки, і зовсім не приваблюють один одного. Їх кінетична енергія залежить від температури. При виведенні закону ідеального газу ми припускаємо, що між частинками немає сил притягання і що частинки не займають жодного місця. Ці два припущення, очевидно, невірні: якщо між частинками немає атракціонів, не було б рідин або твердих речовин. Так само частинки займають трохи місця. Оскільки ми знаємо, що сили привабливості стають важливими при низьких температурах, і що обсяг частинок буде важливим, ми об'єм відносно низький (тобто тиск високий), ми можемо передбачити, що ідеальне рівняння газу найкраще працює при високих температурах і низьких тисках.

    Дописувачі та атрибуція