6.7: Іонні розподіли поблизу зарядженого інтерфейсу

Наближення Дебая-Гюкеля

Опис іонів поблизу негативно зарядженої площини є способом опису дифузного шару катіонів, який утворюється поблизу інтерфейсу негативного заряду в ліпідних бішарах. Найпростіший підхід полягає у використанні рівняння Дебея-Хюкеля (лінеаризованого PBE) в одному вимірі. \(x\)відстань від нескінченної зарядженої площини з поверхневою щільністю заряду\(\sigma = q/a\).

\[\dfrac{\partial^2 \Phi (x)}{\partial x^2} = \dfrac{1}{\lambda_D^2} \Phi (x)\nonumber\]

Як правило, рішення є

\[\Phi (x) = a_1 e^{-x/\lambda_D} + a_2 e^{x/\lambda_D} \label{eq6.7.1}\]

Застосувати граничні умови:

1. \(\lim_{x \to \infty} \Phi (x) = 0\)\(\therefore a_2 = 0\)
2. Електричне поле для поверхні з щільністю заряду σ (з теореми Гаусса)

\[E = - \dfrac{\partial \Phi}{\partial x} |_{\text{surface}} = \dfrac{\sigma}{\varepsilon} \label{eq6.7.2}\]

Диференціювати ур. (\(\ref{eq6.7.1}\)) і порівняти з еквалайзером. (\(\ref{eq6.7.2}\)):

\[a_1 = \dfrac{\sigma \lambda_D}{\varepsilon} \nonumber\]

Електростатичний потенціал розпадається експоненціально від поверхні до нуля.

\[\Phi (x) = \dfrac{\sigma \lambda_D}{\varepsilon} e^{-x/\lambda_D} \nonumber\]

Номінально префактором буде «поверхневий потенціал» на\(x = 0\), але наближення Дебая значно занизило б це, як ми побачимо пізніше. Підстановка\(\Phi\) в рівняння Пуассона дає

\[\rho (x) = \dfrac{-\sigma}{\lambda_D} e^{-x/\lambda_D} \label{eq6.7.3}\]

Щільність розподілу іонів у розчині експоненціально розпадається з відстанню. Цей опис справедливо для слабких потенціалів, або\(x > \lambda_D\). Потенціал і щільність заряду пропорційні як\(\Phi (x) = -\lambda_D^2 \rho (x)/\varepsilon \); обидва розпадаються експоненціально за шкалою довжини Дебая на великому діапазоні.

Примітка:

Більш висока концентрація іонів\(\to\) менша\(\lambda_D \to\) Подвійний шар менш дифузний.

Більш висока температура\(\to\) більша\(\lambda_D \to\) Подвійний шар більш дифузний.

Відзначимо також, що поверхневий заряд врівноважується розподілом іонів в розчині:

\[\sigma = -\int_0^{\infty} \rho (x) dx\]

які ви можете підтвердити, підставивши еквалайзер. (\(\ref{eq6.7.3}\)).

Гуй - Чепмен Модель ¹

Щоб правильно описати поведінку іонів на коротших відстанях (\(x < \lambda_D\)), не потрібно робити слабко-потенційне наближення і можна зберегти нелінійну форму рівняння Пуассона-Больцмана:

\[\begin{array} {rcl} {\dfrac{\partial^2 \Phi (x)}{\partial x^2}} & = & {\dfrac{2zeC_0}{\varepsilon} \text{sinh} \left (\dfrac{ze \Phi (x)}{kT} \right )} \\ {E} & = & {-\dfrac{\partial \Phi}{\partial x}|_{\text{surf}} = \dfrac{4\pi \ell_B \sigma k_B T}{e^2}} \end{array} \nonumber\]

Насправді ця форма дійсно має аналітичне рішення. Корисно визначити безрозмірний зменшений електростатичний потенціал, виражений в теплових електричних агрегатах:

\[\underline{\Phi} = \dfrac{e}{k_B T} \Phi \nonumber\]

і зменшену відстань, яка масштабується довжиною Debye

\[\underline{x} = x/\lambda_D \nonumber \]

Тоді ПБЕ для електроліту 1:1 набуває просту форму

\[\nabla^2 \underline{\Phi} (x) = \text{sinh} \underline{\Phi} (x)\nonumber\]

з розчином:

\[\underline{\Phi} (\underline{x}) = 2 \ln \left (\dfrac{1 + ge^{-\underline{x}}}{1 - ge^{-\underline{x}}} \right )\nonumber\]

\(g\)Ось константа, яку ми можемо співвідносити з поверхневим потенціалом,\(x\) встановивши нуль.

\[\exp (-\underline{\Phi} (0)/2) = \dfrac{1 - g}{1 + g} = -\text{tanh} (\ln (g) /2)\nonumber\]

\(\underline{\Phi} (0)\)масштабований поверхневий потенціал. Використовуючи поверхневу щільність заряду,\(\sigma\) ми можемо знайти:

\[g = - \dfrac{x_0}{\lambda_D} + \sqrt{1 + \left (\dfrac{x_0}{\lambda_D} \right )^2} \text{ with } x_0 = \dfrac{e}{2\pi \ell_B \sigma} \nonumber\]

Тоді ви можете отримати розподіл іонів з рівняння Пуассона:\(\rho (x) = \varepsilon \nabla^2 \Phi (x)\).

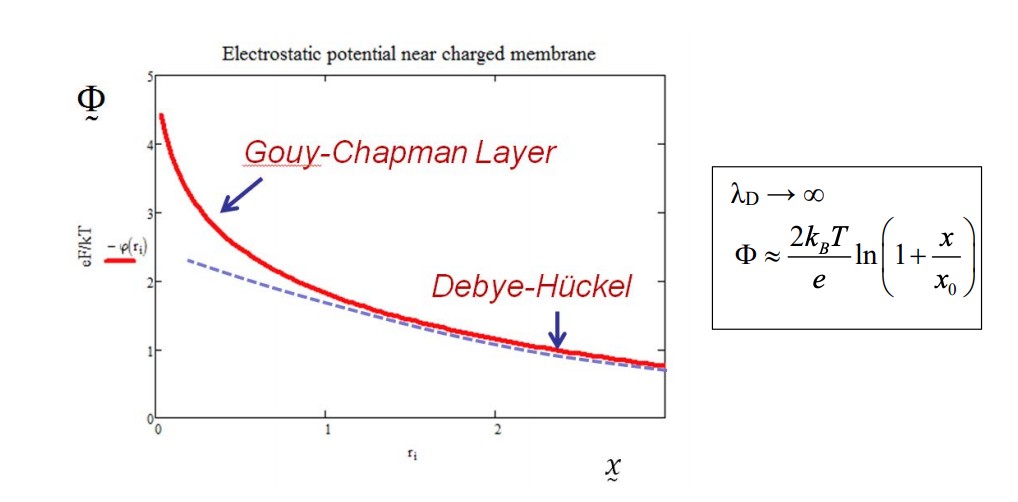
Шар Гуя - Чепмена\(x < \lambda_D\), тобто має досить сильні іонні взаємодії, що ви побачите покращення над Дебі-Хюкелем.

кормовий шар

У безпосередній близькості до сильно зарядженої поверхні можна сформувати на поверхні шар прямих контактів протиіонів: Штерновий шар. Штерновий шар керує площиною ковзання для дифузії заряджених частинок. Дзета-потенціал\(\zeta\) - це різниця енергій потенціалів між шаром Стерна і електронно-нейтральною областю зразка і регулює електрофоретичну рухливість частинок. Вона розраховується з роботи, необхідної для виведення\(x = \infty\) заряду з на поверхню Штернового шару.

_______________________________

1. Girault, Аналітична та фізична електрохімія. (CRC Press, Нью-Йорк, 2004); М.Б. Джексон, Молекулярна та клітинна біофізика. (Кембриджський університетський прес, Кембридж, 2006), гл. 11; М. Даун, Молекулярна біофізика: структури в русі. (Оксфордський університетський прес, Нью-Йорк, 1999), гл. 18.; Маклафлін, Електростатичні властивості мембран, Annu. Преподобний Біофіс. Біофіси. Хім. 18, 113-136 (1989).