Skip to main content
LibreTexts - Ukrayinska

9.1: Поверхні відповіді

  1. Last updated
  2. Save as PDF
  • Page ID
    17589

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

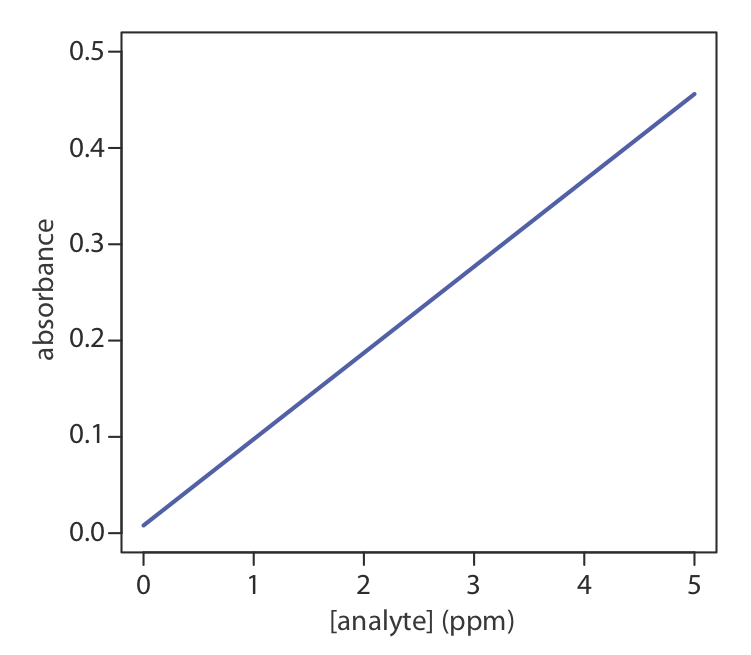
    Одним з найбільш ефективних способів подумати про оптимізацію є візуалізація того, як змінюється реакція системи, коли ми збільшуємо або зменшуємо рівні одного або декількох її факторів. Ми називаємо графік відгуку системи як функцію рівня фактора поверхнею відгуку. Найпростіша поверхня відгуку має один коефіцієнт і малюється у двох вимірах шляхом розміщення відповідей на осі y та рівнях фактора на осі x. Калібрувальна крива на малюнку\(\PageIndex{1}\) є прикладом однофакторної поверхні відгуку. Ми також можемо визначити поверхню відгуку математично. Поверхня відгуку на малюнку\(\PageIndex{1}\), наприклад, є

    \[A = 0.008 + 0.0896C_A \nonumber\]

    де A - поглинання, а C A - концентрація аналіта в проміле.

    Малюнок 14.1. PNG
    Малюнок\(\PageIndex{1}\). Калібрувальна крива є прикладом однофакторної поверхні відгуку. Відповіді (поглинання) побудовані на осі y, а рівні факторів (концентрація аналіту) побудовані на осі x.

    Для двофакторної системи, такої як кількісний аналіз для ванадію, описаний раніше, поверхня відгуку являє собою плоску або вигнуту площину в трьох вимірах. Як показано на малюнку\(\PageIndex{2}\), ми розміщуємо відповідь на вісь z та рівні коефіцієнта на осі x та осі y. \(\PageIndex{2a}\)На малюнку показаний псевдо-тривимірний каркасний графік для системи, яка підпорядковується рівнянню

    \[R = 3.0 - 0.30A + 0.020AB \nonumber\]

    де R - відповідь, а A і B - фактори. Ми також можемо представити двофакторну поверхню відгуку за допомогою двовимірного графіка рівня на малюнку\(\PageIndex{2b}\), який використовує кольоровий градієнт для відображення відповіді на двовимірній сітці, або використовуючи двовимірний контурний графік на малюнку\(\PageIndex{2c}\), який використовує контурні лінії для відображення поверхні відгуку.

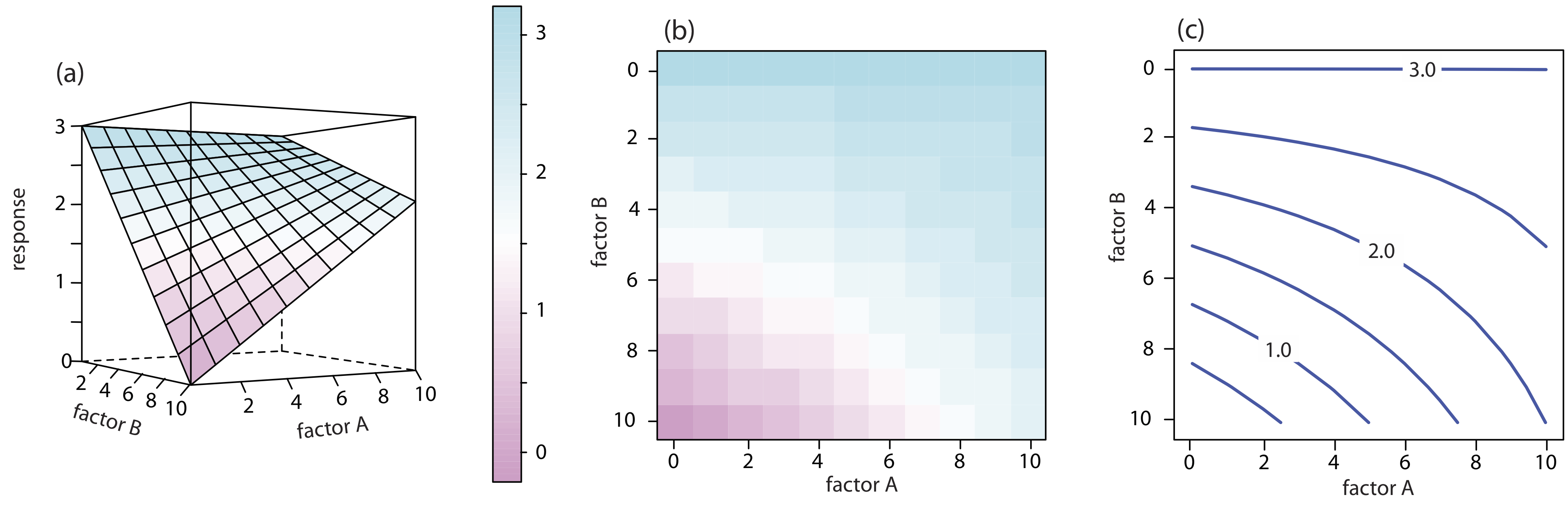
    Малюнок 14.2. PNG
    Малюнок\(\PageIndex{2}\). Три приклади двофакторної поверхні відгуку відображаються у вигляді (а) псевдотривимірного каркасного графіка, (б) двовимірного рівневого графіка та (в) двовимірного контурного графіка. Ми називаємо дисплей у (a) псевдо-тривимірній поверхні відгуку, оскільки ми показуємо наявність трьох вимірів на плоскій двовимірній поверхні сторінки.

    Поверхні відгуку на рисунку\(\PageIndex{2}\) охоплюють обмежений діапазон рівнів факторів (0 ≤ A ≤ 10, 0 ≤ B ≤ 10), але ми можемо розширити кожну з них до більш позитивних або на більше від'ємних значень, оскільки немає обмежень на фактори. Більшість поверхонь відгуку, що цікавлять хіміка-аналітика, мають природні обмеження, накладені факторами, або мають практичні межі, встановлені аналітиком. Наприклад\(\PageIndex{1}\), поверхня відгуку на малюнку має природне обмеження на його коефіцієнт, оскільки концентрація аналіта не може бути меншою за нуль; тобто\(C_A \ge 0\).

    Якщо у нас є рівняння для поверхні відгуку, то знайти оптимальну реакцію відносно легко. На жаль, ми рідко знаємо будь-які корисні подробиці про поверхню відгуку. Натомість ми повинні визначити форму поверхні відгуку та знайти її оптимальну реакцію, виконавши відповідні експерименти. У цій главі основна увага приділяється корисним експериментальним методам характеристики поверхні відгуку. Ці експериментальні методи поділяються на дві великі категорії: методи пошуку, в яких алгоритм керує систематичним пошуком оптимального відгуку, і методи моделювання, в яких ми використовуємо теоретичну модель або емпіричну модель поверхні відгуку для прогнозування оптимальної реакції.