9.2: Алгоритми пошуку

Last updated
Save as PDF

Page ID: 17625

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

\(\PageIndex{1}\)На малюнку зображена частина Бадлендс Південної Дакоти, безплідний ландшафт, який включає багато вузьких хребтів, утворених через ерозію. Припустимо, ви бажаєте піднятися на найвищу точку цього хребта. Оскільки найкоротший шлях до вершини не очевидний, ви можете прийняти наступне просте правило: озирніться навколо себе і зробіть один крок у напрямку, який має найбільшу зміну висоти, а потім повторюйте, поки не буде можливий подальший крок. Маршрут, яким ви прямуєте, є результатом систематичного пошуку, який використовує алгоритм пошуку. Звичайно, існує якомога більше маршрутів, скільки є відправних точок, три приклади яких наведені на малюнку\(\PageIndex{1}\). Зверніть увагу, що деякі маршрути не досягають найвищої точки - те, що ми називаємо глобальним оптимальним. Натомість багато маршрутів закінчуються локальним оптимумом, з якого подальший рух неможливий.

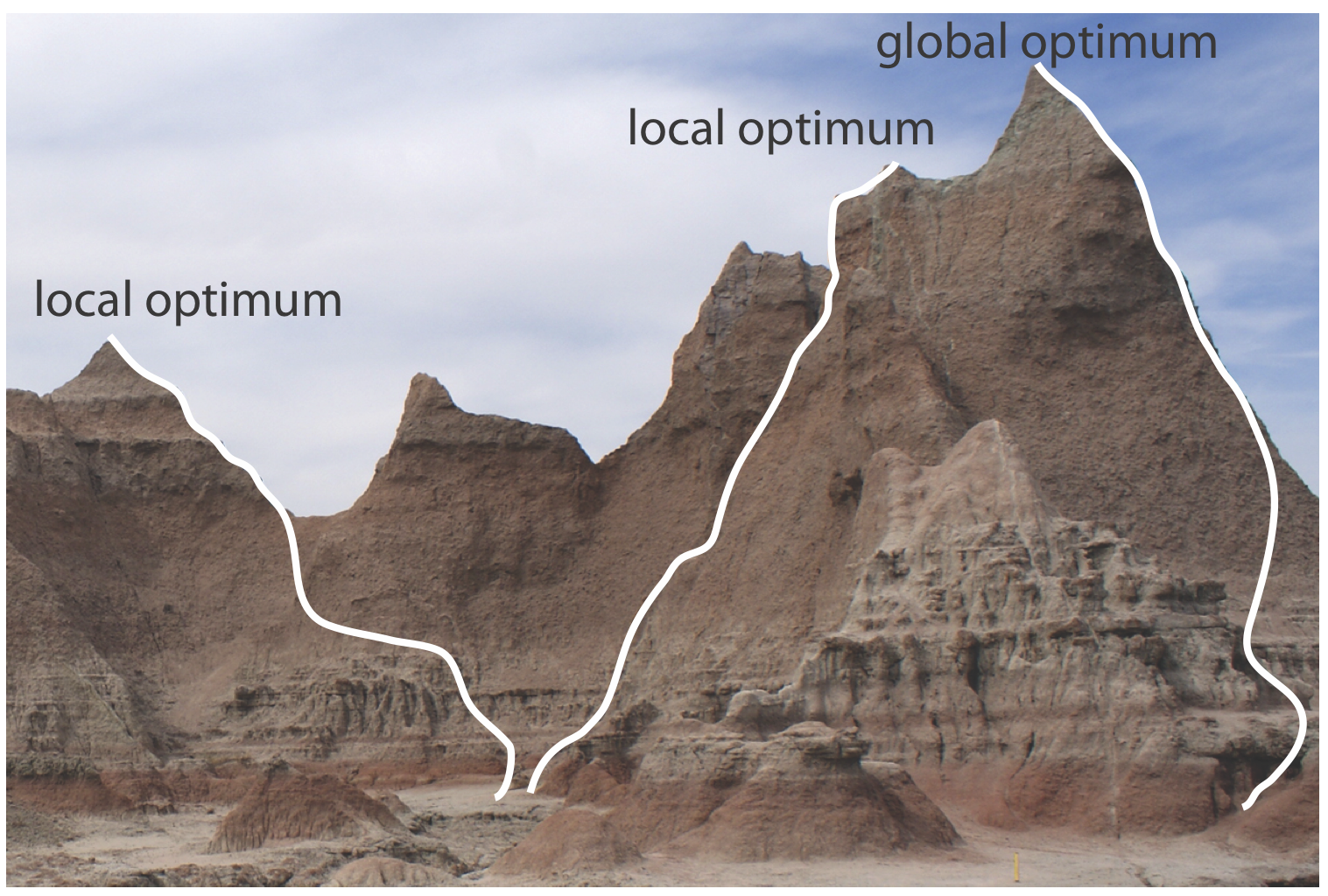
Малюнок 14.3 PNG — Малюнок\(\PageIndex{1}\). Пошук найвищої точки на гребені за допомогою алгоритму пошуку є одним із корисних методів для визначення оптимального місця на поверхні відгуку. Шляхи в крайньому правому куті досягають найвищої точки, або глобального оптимума. Інші два шляхи досягають локальної оптими. Алгоритми пошуку мають назви: описаний тут метод найкрутішого підйому.

Ми можемо використовувати систематичний алгоритм пошуку, щоб знайти оптимальну відповідь. Починаємо з вибору початкового набору рівнів факторів і виміряємо реакцію. Далі ми застосовуємо правила нашого алгоритму пошуку, щоб визначити новий набір рівнів факторів і виміряти його реакцію, продовжуючи цей процес, поки не досягнемо оптимальної відповіді. Перш ніж розглядати два загальних алгоритму пошуку, давайте розглянемо, як ми оцінюємо алгоритм пошуку.

Ефективність і результативність

Алгоритм пошуку характеризується своєю ефективністю та ефективністю. Щоб бути ефективним, алгоритм пошуку повинен знайти глобальний оптимум поверхні відгуку або, принаймні, досягти точки поблизу глобального оптимуму. Пошуковий алгоритм може не знайти глобальний оптимум з кількох причин, включаючи погано розроблений алгоритм, невизначеність у вимірюванні відгуку та наявність локальної оптими. Розглянемо кожну з цих потенційних проблем.

Погано розроблений алгоритм може передчасно закінчити пошук, перш ніж він досягне глобального оптимального рівня поверхні відповіді. Як показано на малюнку\(\PageIndex{2}\), коли ви піднімаєтеся на хребет, який нахиляється на північний схід, алгоритм, швидше за все, зазнає невдачі, якщо обмежує ваші кроки лише на північ, південь, схід чи захід. Алгоритм, який не може реагувати на зміну напрямку найкрутішого підйому, не є ефективним алгоритмом.

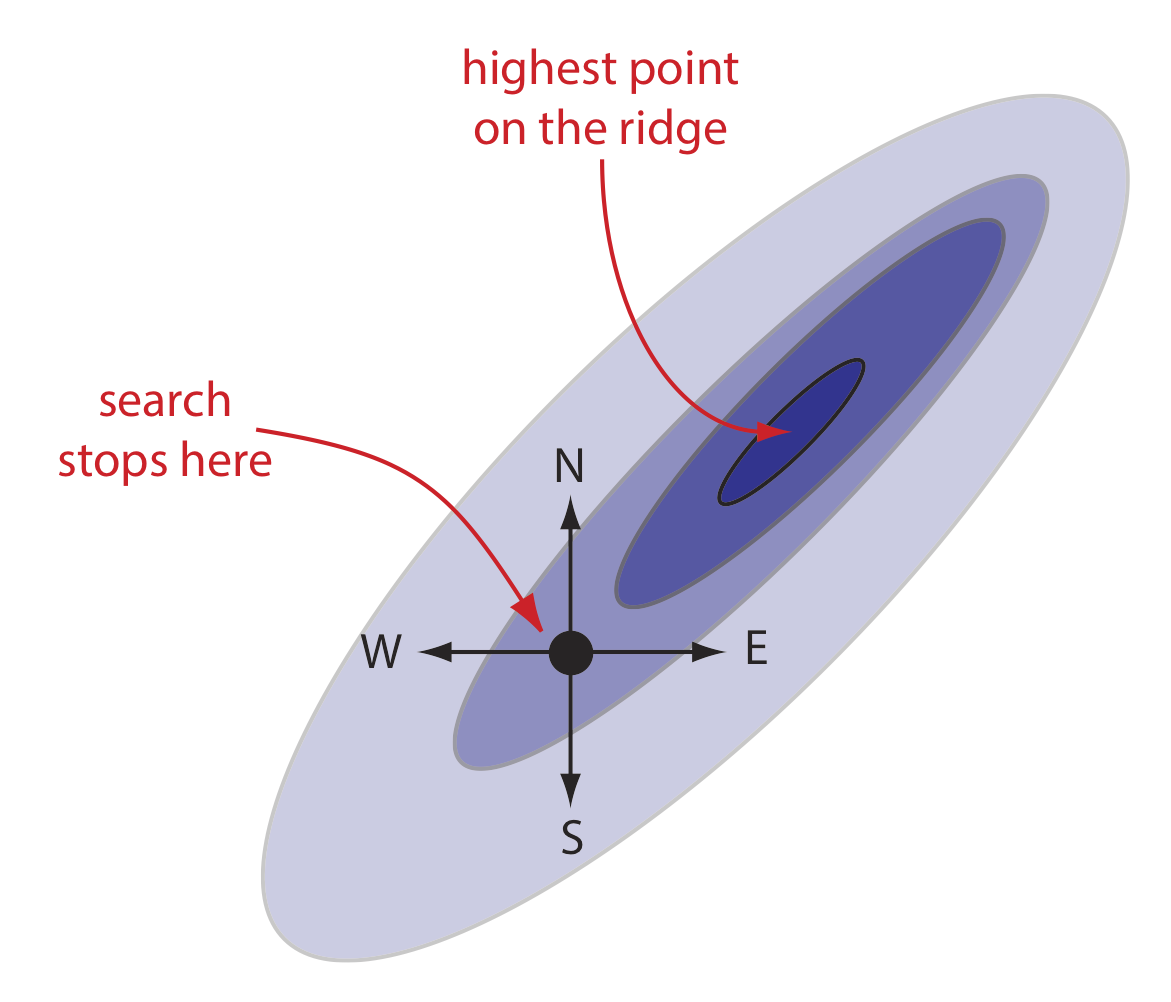
Малюнок 14.4 PNG — Малюнок\(\PageIndex{2}\). Приклад, який показує, як погано розроблений алгоритм пошуку, обмежений переміщенням лише на північ, південь, схід чи захід, може не знайти глобальний оптимум поверхні відповіді.

Усі вимірювання містять невизначеність або шум, який впливає на нашу здатність характеризувати основний сигнал. Коли шум більше, ніж локальна зміна сигналу, то алгоритм пошуку, швидше за все, закінчиться, перш ніж він досягне глобального оптимуму. Малюнок\(\PageIndex{3}\), який надає інший вигляд малюнка\(\PageIndex{1}\), показує нам, що відносно рівна місцевість, що веде до хребта, сильно вивітрюється і дуже нерівномірна. Оскільки зміна локальної висоти (шум) перевищує нахил (сигнал), наш алгоритм пошуку закінчується вперше, коли ми наступаємо на менш вивітрювану місцеву поверхню, яка вище, ніж безпосередньо навколишні поверхні.

Малюнок 14.5 PNG — Малюнок\(\PageIndex{3}\). Інший вид хребта на малюнку\(\PageIndex{1}\), який показує вивітрювану місцевість, що веде до хребта. Жовтий стрижень внизу фігури, який позначає слід, має висоту близько 18 дюймів.

Нарешті, поверхня відгуку може містити кілька локальних оптим, тільки одна з яких є глобальним оптимумом. Якщо ми почнемо пошук поблизу локального оптимуму, наш алгоритм пошуку може ніколи не досягти глобального оптимуму. Коник на малюнку\(\PageIndex{1}\), наприклад, має безліч вершин. Тільки ті пошуки, які починаються в крайньому правому куті, досягнуть найвищої точки на хребті. В ідеалі алгоритм пошуку повинен досягати глобального оптимуму незалежно від того, де він починається.

Алгоритм пошуку завжди досягає оптимального. Наша проблема, звичайно, полягає в тому, що ми не знаємо, чи є це глобальним оптимумом. Одним із методів оцінки ефективності пошукового алгоритму є використання декількох наборів початкових рівнів факторів, пошук оптимальної реакції для кожного та порівняння результатів. Якщо ми приходимо до однієї і тієї ж оптимальної реакції після запуску з дуже різних місць на поверхні відповіді, то ми більш впевнені, що це глобальний оптимум.

Ефективність є другою бажаною характеристикою алгоритму пошуку. Ефективний алгоритм переходить від початкового набору рівнів факторів до оптимальної реакції за якомога менше кроків. Шукаючи найвищу точку на хребті на малюнку\(\PageIndex{3}\), ми можемо збільшити швидкість, з якою ми наближаємось до оптимальної, роблячи більші кроки. Однак, якщо розмір кроку занадто великий, різниця між експериментальним оптимумом і справжнім оптимальним може бути неприпустимо великою. Одним з рішень є коригування розміру кроку під час пошуку, використовуючи більші кроки на початку та менші кроки, коли ми наближаємось до глобального оптимального.