9.4: Симплексна оптимізація
- Page ID
- 17613
Однією зі стратегій підвищення ефективності пошукового алгоритму є зміна більше одного фактора за раз. Зручний спосіб досягти цього, коли є два фактори, - почати з трьох наборів початкових рівнів факторів, розташованих у вигляді вершин трикутника (рис\(\PageIndex{1}\). Виміривши реакцію для кожного набору рівнів факторів, ми визначаємо комбінацію, яка дає найгіршу реакцію, і замінюємо її новим набором рівнів факторів за допомогою набору правил. Цей процес триває до тих пір, поки ми не досягнемо глобального оптимального рівня або поки подальша оптимізація неможлива. Безліч факторних рівнів називається симплексом. Загалом, для k факторів симплекс - це\(k + 1\) розмірна геометрична фігура [див. Спендлі, В.; Хекст, Г. Р.; Хімсворт, Ф. Р. Технометрія 1962, 4, 441—461, і Демінг, С.Н.; Паркер, Л.Р. CRC Crit. Преподобний Анальний. Хім. 1978 7 (3), 187—202]. Таким чином, для двох факторів симплекс - це трикутник. Для трьох факторів симплекс - це тетраедр.
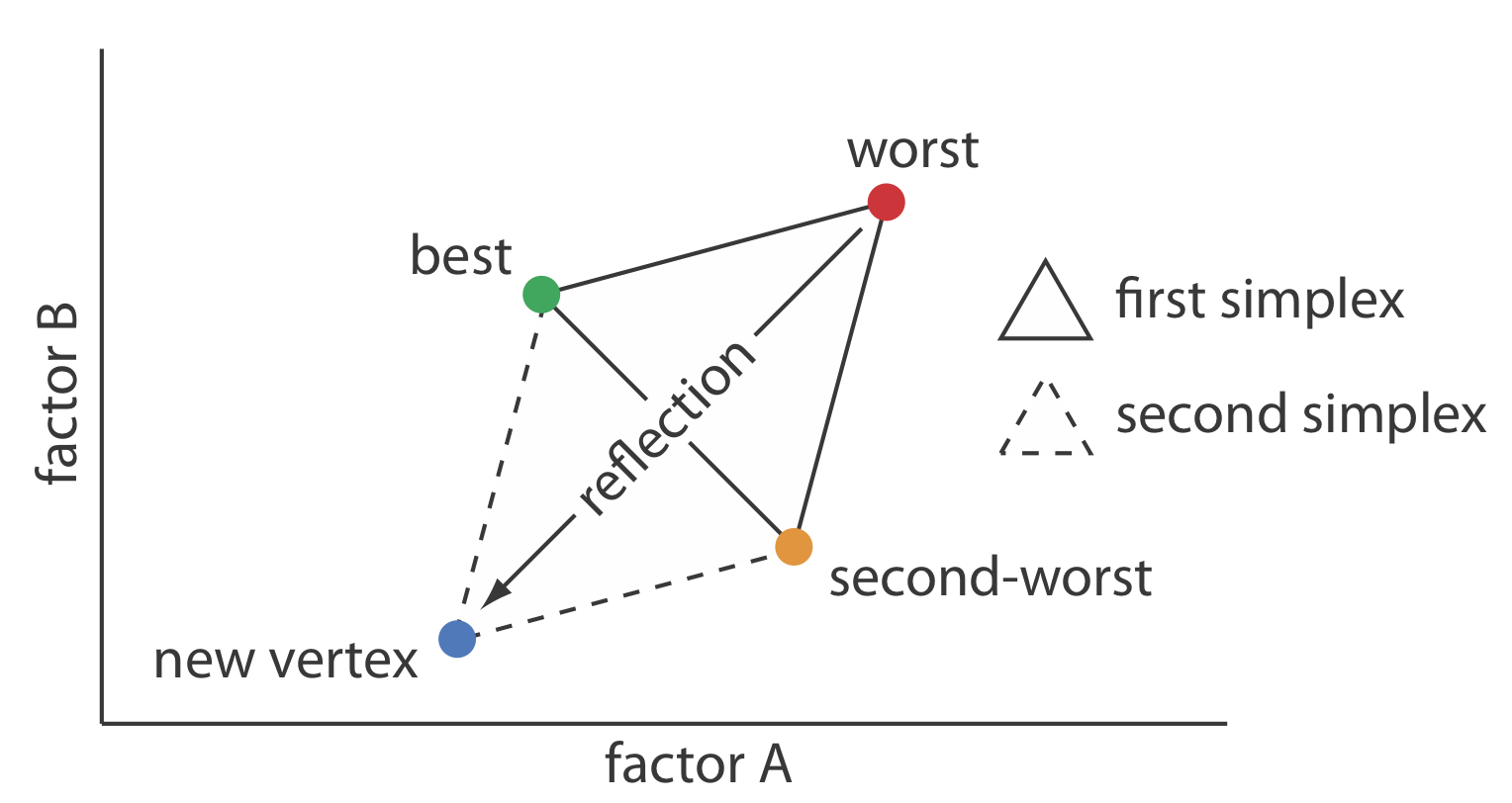
Щоб розмістити початковий двофакторний симплекс на поверхні відгуку, вибираємо початкову точку (a, b) для першої вершини і розміщуємо інші дві вершини в (a + s a, b) і (a + 0. 5с а, б + 0. 87s b) де s a і s b - розміри кроків для фактора A і для фактора B [див., наприклад, Long, D. E. Anal. Чим. Акт 1969, 46, 193—206]. Наступний набір правил переміщує симплекс по поверхні відповіді в пошуках оптимальної реакції:
Правило 1. Оцініть вершини від best (v b) до гіршого (v w).
Правило 2. Відхиліть найгіршу вершину (v w) і замініть її новою вершиною (v n), відбивши найгіршу вершину через середину інших вершин. Рівні фактора нової вершини вдвічі перевищують рівні середніх коефіцієнтів для збережених вершин за вирахуванням рівнів фактора для найгіршої вершини. Для двофакторної оптимізації тут наведено рівняння, де v s - третя вершина.
\[a_{v_n} = 2 \left( \frac {a_{v_b} + a_{v_s}} {2} \right) - a_{v_w} \nonumber \]
\[b_{v_n} = 2 \left( \frac {b_{v_b} + b_{v_s}} {2} \right) - b_{v_w} \nonumber \]
Правило 3. Якщо нова вершина має найгіршу відповідь, поверніться до попередньої вершини та відхиліть вершину з другою найгіршою відповіддю, (v s) обчислюючи рівні фактора нової вершини за допомогою правила 2. Це правило гарантує, що симплекс не повернеться до попереднього симплексу.
Правило 4. Граничні умови є корисним способом обмеження діапазону можливих рівнів факторів. Наприклад, може знадобитися обмежити концентрацію фактора з причин розчинності або обмежити температуру, оскільки реагент термічно нестабільний. Якщо нова вершина перевищує граничну умову, то призначте їй найгіршу відповідь і дотримуйтесь правила 3.
Оскільки розмір симплекса залишається постійним під час пошуку, цей алгоритм називається симплексною оптимізацією фіксованого розміру. Наступний приклад ілюструє застосування цих правил.
Знайти оптимальну для поверхні відгуку, описану рівнянням
\[R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.254 B^2 - 0.0857 AB \nonumber \]
за допомогою алгоритму симплексного пошуку фіксованого розміру. Використовуйте (0, 0) для початкових рівнів коефіцієнта та встановіть розмір кроку кожного фактора на 1,00.
Рішення
Дозволити a = 0, b = 0, s a = 1.00, а s b = 1.00 дає вершини початкового симплексу як
\[\text{vertex 1:} (a, b) = (0, 0) \nonumber\]
\[\text{vertex 2:} (a + s_a, b) = (1.00, 0) \nonumber\]
\[\text{vertex 3:} (a + 0.5s_a, b + 0.87s_b) = (0.50, 0.87) \nonumber\]
Відповіді на три вершини наведені в наступній таблиці
| вершина | a | б | відповідь |
|---|---|---|---|
| \(v_1\) | 0 | 0 | 5.50 |
| \(v_2\) | 1.00 | 0 | 6.85 |
| \(v_3\) | 0,50 | 0,87 | 6.68 |
з\(v_1\) найгіршою реакцією та\(v_3\) найкращою реакцією. Дотримуючись Правило 1, ми\(v_1\) відхиляємо і замінюємо його новою вершиною; таким чином
\[a_{v_4} = 2 \left( \frac {1.00 + 0.50} {2} \right) - 0 = 1.50 \nonumber\]
\[b_{v_4} = 2 \left( \frac {0 + 0.87} {2} \right) - 0 = 0.87 \nonumber\]
Наступна таблиця дає вершини другого симплекса.
| вершина | a | б | відповідь |
|---|---|---|---|
| \(v_2\) | 1,50 | 0 | 6.85 |
| \(v_3\) | 0,50 | 0,87 | 6.68 |
| \(v_4\) | 1,50 | 0,87 | 7.80 |
з\(v_3\) найгіршою реакцією та\(v_4\) найкращою реакцією. Дотримуючись Правило 1, ми\(v_3\) відхиляємо і замінюємо його новою вершиною; таким чином
\[a_{v_5} = 2 \left( \frac {1.00 + 1.50} {2} \right) - 0.50 = 2.00 \nonumber\]
\[b_{v_5} = 2 \left( \frac {0 + 0.87} {2} \right) - 0.87 = 0 \nonumber\]
Наступна таблиця дає вершини третього симплекса.
| вершина | a | б | відповідь |
|---|---|---|---|
| \(v_2\) | 1,50 | 0 | 6.85 |
| \(v_4\) | 1,50 | 0,87 | 780 |
| \(v_5\) | 2.00 | 0 | 7.90 |
Обчислення інших вершин залишають як вправу. \(\PageIndex{2}\)На малюнку показаний хід повної оптимізації. Після 29 кроків симплекс починає повторюватися, кружлячи навколо оптимальної реакції (3, 7).
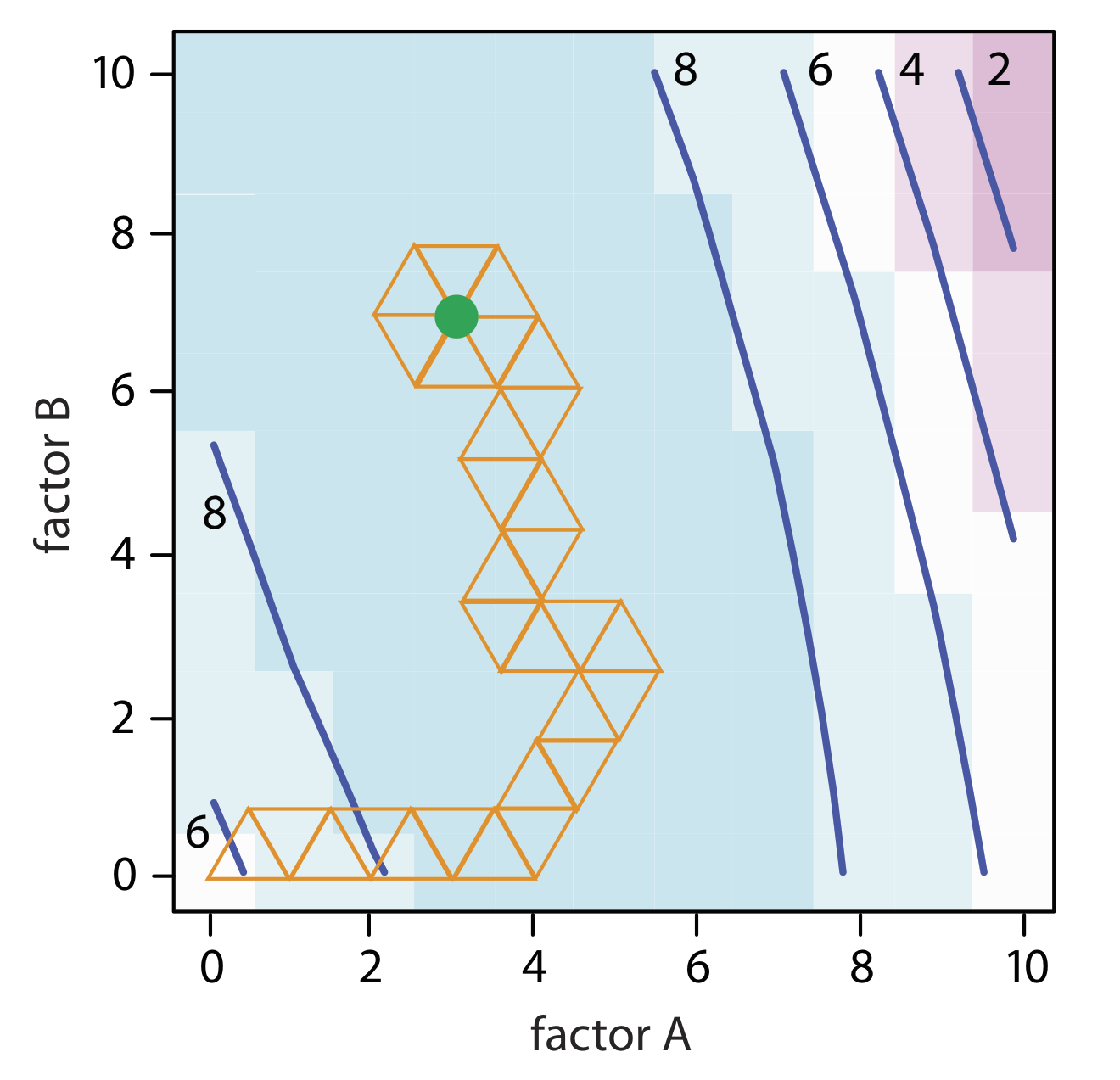
Розмір початкового симплексу в кінцевому підсумку обмежує ефективність і ефективність алгоритму симплексного пошуку фіксованого розміру. Ми можемо підвищити його ефективність, дозволивши розміру симплекса розширюватися або скорочуватися у відповідь на швидкість, з якою ми наближаємося до оптимальної. Наприклад, якщо ми виявимо, що нова вершина краще будь-якої з вершин в попередньому симплексі, то розгортаємо симплекс далі в цьому напрямку з припущення, що рухаємося безпосередньо до оптимального. Інші умови можуть змусити нас укласти простий - щоб зробити його меншим - щоб заохотити оптимізацію рухатися в іншому напрямку. Ми називаємо це симплексною оптимізацією змінного розміру. Зверніться до додаткових ресурсів цієї глави для отримання додаткової інформації про симплексну оптимізацію змінного розміру.
