8.1: Незважена лінійна регресія з помилками у y
- Page ID
- 17979
Найбільш поширений метод завершення лінійної регресії робить три припущення:
- різниця між нашими експериментальними даними та обчисленою лінією регресії є результатом невизначеної помилки, що впливають на y
- будь-які невизначені помилки, які впливають на y, зазвичай розподіляються
- що невизначені помилки в y не залежать від значення x
Оскільки ми припускаємо, що невизначені помилки однакові для всіх стандартів, кожен стандарт однаково вносить свій внесок у нашу оцінку нахилу та y -перехоплення. З цієї причини результат вважається незваженою лінійною регресією.
Друге припущення, як правило, вірно через центральну граничну теорему, яку ми розглянули в розділі 5.3. Обґрунтованість двох інших припущень менш очевидна, і ви повинні оцінити їх, перш ніж приймати результати лінійної регресії. Зокрема, перше припущення завжди підозрюється, оскільки, безумовно, є певна невизначена похибка вимірювання x. Коли ми готуємо калібрувальну криву, однак, незвично виявити, що невизначеність у сигналі, S, значно більша, ніж невизначеність концентрації аналіта\(C_A\). За таких обставин перше припущення зазвичай є розумним.
Як працює лінійна регресія
Щоб зрозуміти логіку лінійної регресії, розглянемо приклад на малюнку\(\PageIndex{1}\), який показує три точки даних і дві можливі прямі лінії, які можуть обґрунтовано пояснити дані. Як ми вирішуємо, наскільки добре ці прямі лінії підходять до даних, і як ми можемо визначити, яка, якщо так, є найкращою прямою лінією?
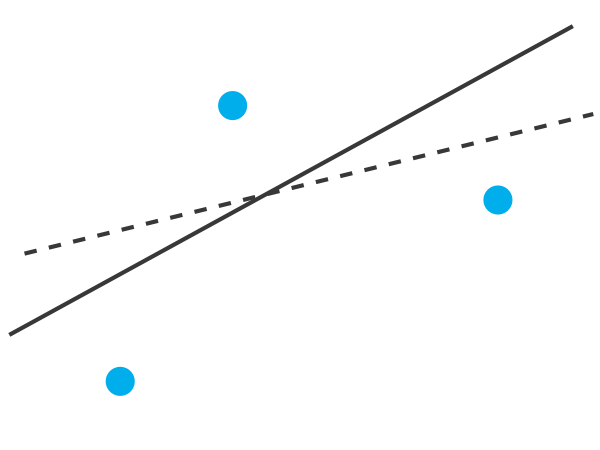
Давайте зосередимося на суцільній лінії на малюнку\(\PageIndex{1}\). Рівняння для цього рядка
\[\hat{y} = b_0 + b_1 x \nonumber \]
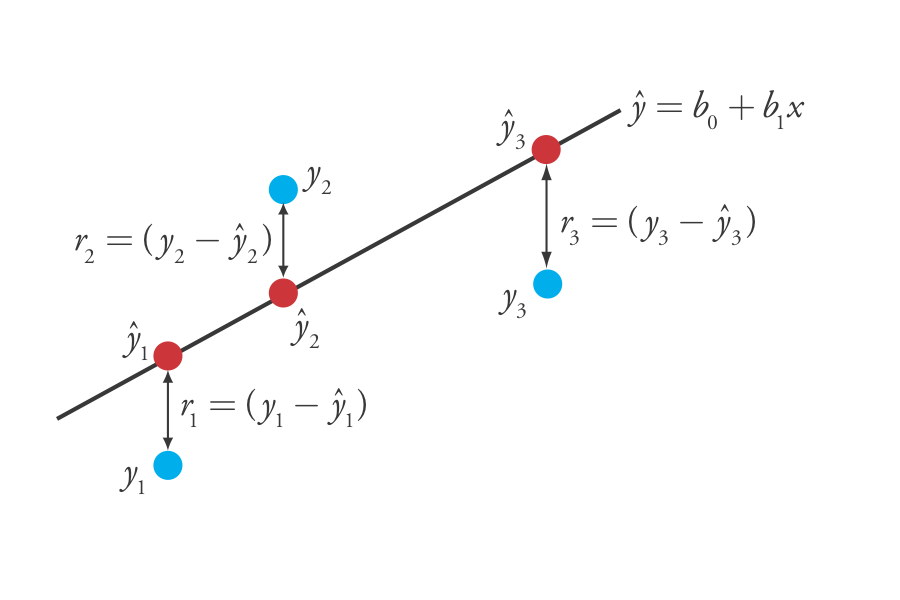
де b 0 і b 1 - оцінки для y -перехоплення та нахилу, і\(\hat{y}\) є прогнозованим значенням y для будь-якого значення x. Оскільки ми припускаємо, що вся невизначеність є результатом невизначеної помилки у, різниця між y і\(\hat{y}\) для кожного значення x є залишковою похибкою, r, в нашій математичній моделі.
\[r_i = (y_i - \hat{y}_i) \nonumber\]
\(\PageIndex{2}\)На малюнку показані залишкові помилки для трьох точок даних. Чим менше загальна залишкова помилка, R, яку ми визначаємо як
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \nonumber \]
тим краще прилягання між прямою лінією і даними. У лінійному регресійному аналізі ми шукаємо значення b 0 та b 1, які дають найменшу загальну залишкову похибку.
Причиною квадратизації окремих залишкових помилок є запобігання позитивної залишкової помилки від скасування негативної залишкової помилки. Ви бачили це раніше в рівняннях для вибірки і популяції стандартних відхилень, введені в главі 4. З цього рівняння також видно, чому лінійну регресію іноді називають методом найменших квадратів.
Пошук нахилу та y -перехоплення для регресійної моделі
Хоча формально ми не будемо розробляти математичні рівняння для лінійного регресійного аналізу, ви можете знайти похідні в багатьох стандартних статистичних текстах [Див., наприклад, Draper, Н.Р.; Smith, H. Прикладний регресійний аналіз, 3-е видання; Wiley: Нью-Йорк, 1998]. Отримане рівняння для ухилу, b 1, дорівнює
\[b_1 = \frac {n \sum_{i = 1}^{n} x_i y_i - \sum_{i = 1}^{n} x_i \sum_{i = 1}^{n} y_i} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2} \nonumber \]
і рівняння для y -перехоплення, b 0, дорівнює
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \nonumber \]
Хоча ці рівняння здаються грізними, необхідно лише оцінити наступні чотири підсумовування
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber\]
Багато калькуляторів, електронних таблиць та інших статистичних програмних пакетів здатні виконувати лінійний регресійний аналіз на основі цієї моделі; докладніше про завершення лінійного регресійного аналізу за допомогою R. наступний приклад.
Використовуючи дані калібрування в наступній таблиці, визначте взаємозв'язок між сигналом та концентрацією аналіта\(x_i\), використовуючи незважену лінійну регресію.\(y_i\)
Рішення
Ми починаємо з налаштування таблиці, яка допоможе нам організувати розрахунок.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (x_i y_i\) ">0.000 | \ (x_i ^ 2\) ">0.000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (x_i\) ">1.236 | \ (x_i^2\) ">0,010 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (x_i\) ">4.966 | \ (x_i^2\) ">0,040 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (x_i\) ">10.773 | \ (x_i^2\) ">0,090 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (x_i\) ">19.516 | \ (x_i^2\) ">0.160 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (x_i\) ">30.210 | \ (x_i^2\) ">0,250 |
Додавання значень у кожному стовпці дає
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber\]
Підставляючи ці значення в рівняння для нахилу і y -перехоплення дає
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber\]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber\]
Взаємозв'язок між\(S\) сигналом та концентрацією аналіта\(C_A\), отже, становить
\[S = 120.71 \times C_A + 0.21 \nonumber\]
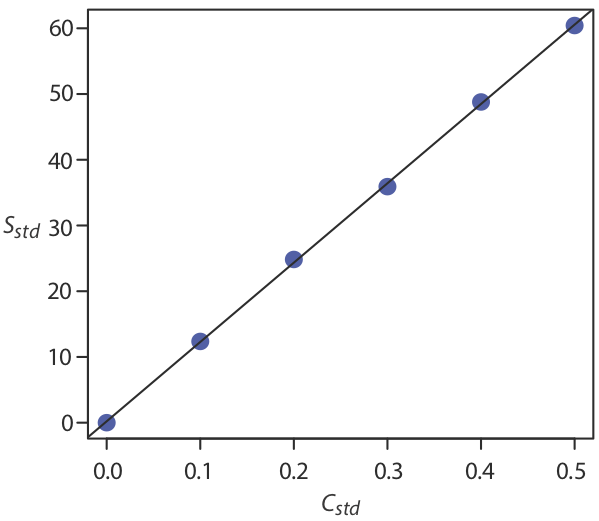
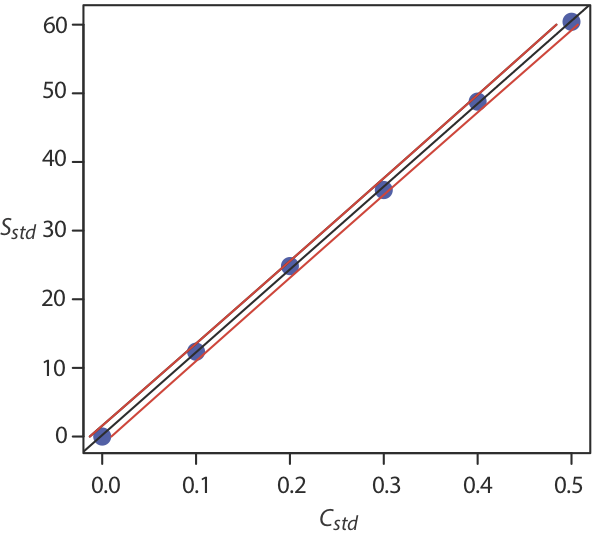
Наразі ми зберігаємо два знака після коми, щоб відповідати кількості десяткових знаків у сигналі. Отримана калібрувальна крива показана на малюнку\(\PageIndex{3}\).
Невизначеність у регресійній моделі
Як ми бачимо на малюнку\(\PageIndex{3}\), через невизначені помилки в сигналі лінія регресії не проходить через точний центр кожної точки даних. Сукупне відхилення наших даних від лінії регресії - загальна залишкова похибка - пропорційно невизначеності в регресії. Ми називаємо цю невизначеність стандартним відхиленням про регресію, s r, яка дорівнює
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \nonumber \]
де y i - i експериментальне значення, і\(\hat{y}_i\) відповідне значення, передбачене рівнянням регресії\(\hat{y} = b_0 + b_1 x\). Зауважте, що знаменник вказує на те, що наш регресійний аналіз має n - 2 ступеня свободи - ми втрачаємо два ступені свободи, оскільки використовуємо два параметри, нахил і y -перехоплення, для обчислення\(\hat{y}_i\).
Більш корисним поданням невизначеності в нашому регресійному аналізі є врахування впливу невизначених помилок на нахил, b 1, і y -перехоплення, b 0, який ми виражаємо як стандартні відхилення.
\[s_{b_1} = \sqrt{\frac {n s_r^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2} {\sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
\[s_{b_0} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
Ми використовуємо ці стандартні відхилення для встановлення довірчих інтервалів для очікуваного нахилу та очікуваного y -перехоплення,\(\beta_1\)\(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \nonumber \]
\[\beta_0 = b_0 \pm t s_{b_0} \nonumber \]
де виділено t для рівня значущості,\(\alpha\) а для n — 2 ступенів свободи. Зауважте, що ці рівняння не містять коефіцієнта, що\((\sqrt{n})^{-1}\) спостерігається у довірчих\(\mu\) інтервалах для розділу 6.2; це пов'язано з тим, що довірчий інтервал тут базується на одній лінії регресії.
Обчисліть 95% довірчих інтервалів для нахилу та y -перехоплення з Прикладу\(\PageIndex{1}\).
Рішення
Почнемо з розрахунку стандартного відхилення про регресію. Для цього ми повинні обчислити передбачені сигнали\(\hat{y}_i\), використовуючи нахил і y -перехоплення з Прикладу\(\PageIndex{1}\), і квадрати залишкової похибки,\((y_i - \hat{y}_i)^2\). Використовуючи останній стандарт як приклад, ми виявимо, що передбачуваний сигнал
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber\]
і що квадрат залишкової похибки
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber\]
Наступна таблиця відображає результати для всіх шести рішень.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) |
\(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (\ hat {y} _i\) ">0.209 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0437 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (\ hat {y} _i\) ">12.280 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0064 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (\ hat {y} _i\) ">24.350 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2304 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (\ hat {y} _i\) ">36.421 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2611 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (\ hat {y} _i\) ">48.491 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0894 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (\ hat {y} _i\) ">60.562 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0202 |
Складання даних в останньому стовпці дає чисельник у рівнянні для стандартного відхилення про регресію; таким чином
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber\]
Далі обчислюємо стандартні відхилення для ухилу і y -перехоплення. Значення термінів підсумовування взяті з Приклад\(\PageIndex{1}\).
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber\]
Нарешті, 95% довірчих інтервалів (\(\alpha = 0.05\)4 ступеня свободи) для нахилу та y -перехоплення є
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber\]
де t (0,05, 4) з додатка 2 дорівнює 2.78. Стандартне відхилення щодо регресії, s r, говорить про те, що сигнал, S std, точний до одного знака після коми. З цієї причини ми повідомляємо нахил і y -перехоплення до одного знака після коми.
Використання моделі регресії для визначення значення для x, заданого значення для y
Після того, як ми отримаємо наше рівняння регресії, легко визначити концентрацію аналіту в зразку. Наприклад, коли ми використовуємо нормальну калібрувальну криву, ми вимірюємо сигнал для нашого зразка, S samp, і обчислюємо концентрацію аналіта, C A, використовуючи рівняння регресії.
\[C_A = \frac {S_{samp} - b_0} {b_1} \nonumber \]
Менш очевидним є те, як повідомити про довірчий інтервал для C A, який виражає невизначеність в нашому аналізі. Для обчислення довірчого інтервалу нам потрібно знати стандартне відхилення в концентрації аналіта\(s_{C_A}\), яке задається наступним рівнянням
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{S}_{samp} - \overline{S}_{std} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( C_{std_i} - \overline{C}_{std} \right)^2}} \nonumber\]
де m - кількість реплікацій, які ми використовуємо для встановлення середнього сигналу зразка, S samp, n - кількість калібрувальних стандартів, S std - середній сигнал для калібрування стандарти,\(C_{std_i}\) і\(\overline{C}_{std}\) є індивідуальними та середніми концентраціями для стандартів калібрування. Знаючи значення\(s_{C_A}\), довірчий інтервал для концентрації аналіта становить
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber\]
де\(\mu_{C_A}\) - очікуване значення С А при відсутності детермінантних похибок, а при значенні t базується на бажаному рівні довіри і n — 2 ступеня свободи.
Ретельне вивчення цих рівнянь повинно переконати вас, що ми можемо зменшити невизначеність прогнозованої концентрації аналіту,\(C_A\) якщо ми збільшимо кількість стандартів\(n\), збільшимо кількість повторюваних зразків, які ми аналізуємо\(m\), і якщо середній сигнал зразка, \(\overline{S}_{samp}\), Прирівнюється до середнього сигналу за стандартами,\(\overline{S}_{std}\). Коли це практично, слід спланувати калібрувальну криву так, щоб S samp потрапляла посередині калібрувальної кривої. Для отримання додаткової інформації про ці рівняння регресії див. (а) Міллер, Дж. Аналітик 1991, 116, 3—14; (б) Шараф, М.А.; Іллман, Д.Л.; Ковальський, Б.Р. Хемометрика, Wiley-Interscience: Нью-Йорк, 1986, стор. 126-127; (c) Комітет з аналітичних методів» Невизначеність концентрацій, оцінених в результаті калібрувальних експериментів», Технічний бриф КУА, березень 2006.
Рівняння стандартного відхилення в концентрації аналіта записано в терміні калібрувального експерименту. Тут наведено більш загальну форму рівняння, записаного через x і y.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber\]
Три репліковані аналізи для зразка, який містить невідому концентрацію аналіту, дає значення для S samp 29,32, 29.16 та 29.51 (довільні одиниці). Використовуючи результати з\(\PageIndex{1}\) Example and Example\(\PageIndex{2}\), визначити концентрацію аналіта, C A та його 95% довірчий інтервал.
Рішення
Середній сигнал становить 29.33, який, використовуючи нахил і y -перехоплення з Прикладу\(\PageIndex{1}\), дає концентрацію аналіта як\(\overline{S}_{samp}\)
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber\]
Щоб розрахувати стандартне відхилення для концентрації аналіта, ми повинні визначити значення для\(\overline{S}_{std}\) і за\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). Перший - це якраз середній сигнал по нормам калібрування, який, використовуючи дані в таблиці\(\PageIndex{1}\), дорівнює 30.385. Обчислення\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) виглядає грізним, але ми можемо спростити його обчислення, визнавши, що ця сума квадратів є чисельником у рівнянні стандартного відхилення; таким чином,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber\]
де\(s_{C_{std}}\) - стандартне відхилення для концентрації аналіту в нормах калібрування. Використовуючи дані в таблиці,\(\PageIndex{1}\) ми знаходимо, що\(s_{C_{std}}\) це 0.1871 і
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber\]
Підставляємо відомі значення в рівняння для\(s_{C_A}\) дач
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber\]
Нарешті, 95% довірчий інтервал для 4 ступенів свободи
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber\]
\(\PageIndex{4}\)На малюнку показана калібрувальна крива з кривими, що показують 95% довірчий інтервал для C A.
Оцінка регресійної моделі
Ніколи не слід приймати результат лінійного регресійного аналізу без оцінки достовірності моделі. Мабуть, найпростішим способом оцінки регресійного аналізу є вивчення залишкових помилок. Як ми бачили раніше, залишкова похибка для єдиного стандарту калібрування, r i, дорівнює
\[r_i = (y_i - \hat{y}_i) \nonumber\]
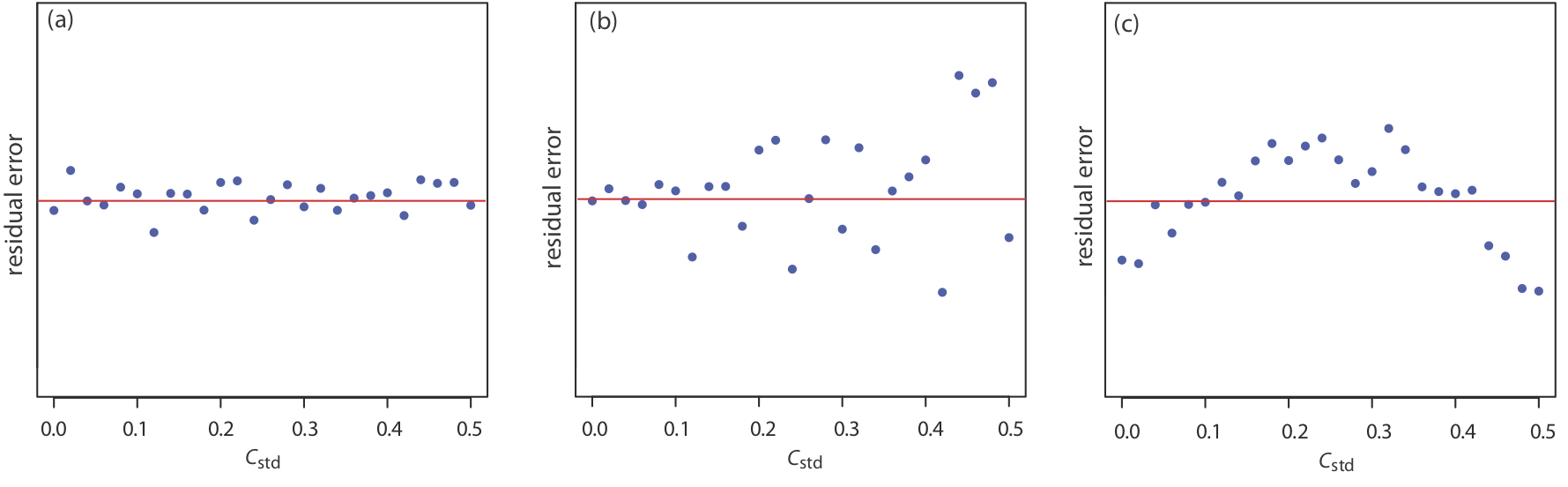
Якщо модель регресії дійсна, то залишкові помилки повинні розподілятися випадковим чином щодо середньої залишкової похибки нуля, без видимої тенденції до менших або більших залишкових помилок (рис.\(\PageIndex{5a}\)). Такі тенденції, як у малюнку\(\PageIndex{5b}\) та малюнку,\(\PageIndex{5c}\) свідчать про те, що принаймні одне з припущень моделі є неправильним. Наприклад, тенденція до більших залишкових помилок при більш високих концентраціях, Рисунок\(\PageIndex{5b}\), свідчить про те, що невизначені помилки, що впливають на сигнал, не залежать від концентрації аналіта. На малюнку\(\PageIndex{5c}\) залишкові помилки не є випадковими, що говорить про те, що ми не можемо моделювати дані за допомогою прямолінійного співвідношення. Регресійні методи для останніх двох випадків розглядаються в наступних розділах.
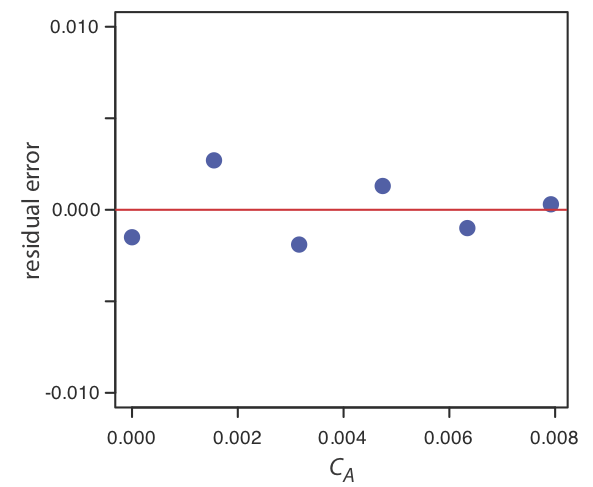
Використовуйте свої результати з вправи,\(\PageIndex{1}\) щоб побудувати залишковий сюжет і пояснити його значення.
Рішення
Для створення залишкової ділянки нам потрібно обчислити залишкову похибку для кожного стандарту. Наступна таблиця містить відповідну інформацію.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) | \(y_i - \hat{y}_i\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.000 | \ (\ hat {y} _i\) ">0.0015 | \ (y_i -\ hat {y} _i\) ">—0.0015 |
| \ (x_i\) ">\(1.55 \times 10^{-3}\) | \ (y_i\) ">0,050 | \ (\ hat {y} _i\) ">0.0473 | \ (y_i -\ hat {y} _i\) ">0.0027 |
| \ (x_i\) ">\(3.16 \times 10^{-3}\) | \ (y_i\) ">0,093 | \ (\ hat {y} _i\) ">0.0949 | \ (y_i -\ hat {y} _i\) ">—0.0019 |
| \ (x_i\) ">\(4.74 \times 10^{-3}\) | \ (y_i\) ">0.143 | \ (\ hat {y} _i\) ">0.1417 | \ (y_i -\ hat {y} _i\) ">0.0013 |
| \ (x_i\) ">\(6.34 \times 10^{-3}\) | \ (y_i\) ">0.188 | \ (\ hat {y} _i\) ">0.1890 | \ (y_i -\ hat {y} _i\) ">—0,0010 |
| \ (x_i\) ">\(7.92 \times 10^{-3}\) | \ (y_i\) ">0,236 | \ (\ hat {y} _i\) ">0.2357 | \ (y_i -\ hat {y} _i\) ">0.0003 |
На малюнку нижче показана схема отриманих залишкових помилок. Залишкові помилки з'являються випадковими, хоча вони чергуються за знаком, і вони не виявляють значної залежності від концентрації аналіта. Разом ці спостереження свідчать про те, що наша регресійна модель є доречною.
