8.2: Зважена лінійна регресія з помилками у y

Last updated
Save as PDF

Page ID: 18002

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Наша обробка лінійної регресії до цього моменту передбачає, що будь-які невизначені помилки, які впливають на y, не залежать від значення x. Якщо це припущення помилкове, то ми повинні включити дисперсію для кожного значення y в наше визначення y -перехоплення, b ₀, і нахилу, b ₁; таким чином

\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \nonumber \]

\[b_1 = \frac {n \sum_{i = 1}^{n} w_i x_i y_i - \sum_{i = 1}^{n} w_i x_i \sum_{i = 1}^{n} w_i y_i} {n \sum_{i =1}^{n} w_i x_i^2 - \left( \sum_{i = 1}^{n} w_i x_i \right)^2} \nonumber\]

де w _i - ваговий коефіцієнт, який враховує дисперсію в y _i

\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \nonumber\]

і\(s_{y_i}\) є стандартним відхиленням для y _i. У зваженій лінійній регресії внесок кожної xy -пари в лінію регресії обернено пропорційний точності y _i; тобто чим точніше значення y, тим більший її внесок у регресію.

Приклад\(\PageIndex{4}\)

Тут наведені дані для зовнішньої стандартизації, в якій s _std є стандартним відхиленням для трьох реплікаційних визначення сигналу. Це ті ж дані, що використовуються в прикладах в розділі 8.1 з додатковою інформацією про стандартні відхилення сигналу.

\(C_{std}\)(довільні одиниці)	\(S_{std}\)(довільні одиниці)	\(s_{std}\)
\ (C_ {std}\) (довільні одиниці виміру) ">0.000	\ (S_ {std}\) (довільні одиниці виміру) ">0.00	\ (s_ {std}\) ">0.02
\ (C_ {std}\) (довільні одиниці виміру) ">0.100	\ (S_ {std}\) (довільні одиниці виміру) ">12.36	\ (s_ {std}\) ">0.02
\ (C_ {std}\) (довільні одиниці виміру) ">0.200	\ (S_ {std}\) (довільні одиниці виміру) ">24.83	\ (s_ {std}\) ">0.07
\ (C_ {std}\) (довільні одиниці виміру) ">0.300	\ (S_ {std}\) (довільні одиниці виміру) ">35.91	\ (s_ {std}\) ">0.13
\ (C_ {std}\) (довільні одиниці виміру) ">0.400	\ (S_ {std}\) (довільні одиниці виміру) ">48.79	\ (s_ {std}\) ">0.22
\ (C_ {std}\) (довільні одиниці виміру) ">0.500	\ (S_ {std}\) (довільні одиниці виміру) ">60.42	\ (s_ {std}\) ">0.33

Визначте рівняння калібрувальної кривої за допомогою зваженої лінійної регресії. Коли ви працюєте над цим прикладом, пам'ятайте, що x відповідає C _std, а що y відповідає S _std.

Рішення

Ми починаємо з налаштування таблиці, яка допоможе в обчисленні вагових коефіцієнтів.

\(C_{std}\)(довільні одиниці)	\(S_{std}\)(довільні одиниці)	\(s_{std}\)	\((s_{y_i})^{-2}\)	\(w_i\)
\ (C_ {std}\) (довільні одиниці виміру) ">0.000	\ (S_ {std}\) (довільні одиниці виміру) ">0.00	\ (s_ {std}\) ">0.02	\ (s_ {y_i}) ^ {-2}\) ">2500.00	\ (w_i\) ">2.8339
\ (C_ {std}\) (довільні одиниці виміру) ">0.100	\ (S_ {std}\) (довільні одиниці виміру) ">12.36	\ (s_ {std}\) ">0.02	\ (s_ {y_i}) ^ {-2}\) ">250.00	\ (w_i\) ">2.8339
\ (C_ {std}\) (довільні одиниці виміру) ">0.200	\ (S_ {std}\) (довільні одиниці виміру) ">24.83	\ (s_ {std}\) ">0.07	\ (s_ {y_i}) ^ {-2}\) ">204.08	\ (w_i\) ">0.2313
\ (C_ {std}\) (довільні одиниці виміру) ">0.300	\ (S_ {std}\) (довільні одиниці виміру) ">35.91	\ (s_ {std}\) ">0.13	\ (s_ {y_i}) ^ {-2}\) ">59,17	\ (w_i\) ">0.0671
\ (C_ {std}\) (довільні одиниці виміру) ">0.400	\ (S_ {std}\) (довільні одиниці виміру) ">48.79	\ (s_ {std}\) ">0.22	\ (s_ {y_i}) ^ {-2}\) ">20.66	\ (w_i\) ">0.0234
\ (C_ {std}\) (довільні одиниці виміру) ">0.500	\ (S_ {std}\) (довільні одиниці виміру) ">60.42	\ (s_ {std}\) ">0.33	\ (s_ {y_i}) ^ {-2}\) ">9.18	\ (w_i\) ">0.0104

Складання значень у четвертому стовпці дає

\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber\]

які ми використовуємо для обчислення окремих ваг в останньому стовпці. Як перевірки на ваших розрахунках сума окремих ваг повинна дорівнювати числу калібрувальних нормативів, n. Сума записів в останньому стовпці дорівнює 6.0000, тому все добре. Після того, як ми обчислимо окремі ваги, ми використовуємо другу таблицю, щоб допомогти в обчисленні чотирьох термінів підсумовування в рівняннях для нахилу\(b_1\), і y -перехоплення,\(b_0\).

\(x_i\)	\(y_i\)	\(w_i\)	\(w_i x_i\)	\(w_i y_i\)	\(w_i x_i^2\)	\(w_i x_i y_i\)
\ (x_i\) ">0.000	\ (y_i\) ">0.00	\ (w_i\) ">2.8339	\ (w_i x_i\) ">0,0000	\ (w_i y_i\) ">0,0000	\ (w_i x_i^2\) ">0,0000	\ (w_i x_i y_i\) ">0,0000
\ (x_i\) ">0.100	\ (y_i\) ">12,36	\ (w_i\) ">2.8339	\ (w_i x_i\) ">0.2834	\ (w_i\) ">35.0270	\ (w_i x_i^2\) ">0.0283	\ (w_i x_i\) ">3.5027
\ (x_i\) ">0,200	\ (y_i\) ">24.83	\ (w_i\) ">0.2313	\ (w_i x_i\) ">0.0463	\ (w_i\) ">5.7432	\ (w_i x_i^2\) ">0,0093	\ (w_i x_i\) ">1.1486
\ (x_i\) ">0,300	\ (y_i\) ">35.91	\ (w_i\) ">0.0671	\ (w_i x_i\) ">0.0201	\ (w_i\) ">2.4096	\ (w_i x_i^2\) ">0,0060	\ (w_i x_i\) ">0.7229
\ (x_i\) ">0,400	\ (y_i\) ">48.79	\ (w_i\) ">0.0234	\ (w_i x_i\) ">0,0094	\ (w_i\) ">1.1417	\ (w_i x_i^2\) ">0.0037	\ (w_i x_i\) ">0,4567
\ (x_i\) ">0,500	\ (y_i\) ">60.42	\ (w_i\) ">0.0104	\ (w_i x_i\) ">0,0052	\ (w_i\) ">0.6284	\ (w_i x_i^2\) ">0,0026	\ (w_i x_i\) ">0.3142

Додавання значень в останніх чотирьох стовпцях дає

\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber\]

який дає розрахунковий ухил і розрахунковий y -перехоплення як

\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber\]

\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber\]

Рівняння калібрування

\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber\]

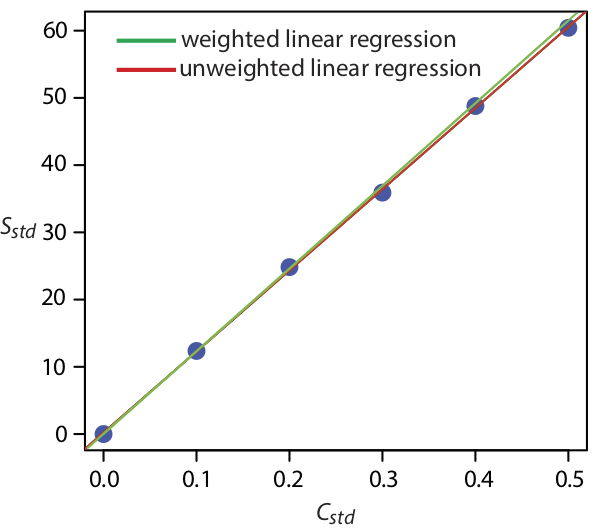
\(\PageIndex{1}\)На малюнку показана калібрувальна крива для зваженої регресії, визначеної тут, та калібрувальну криву для незваженої регресії з розділу 8.2. Хоча дві калібрувальні криві дуже схожі, є невеликі відмінності в нахилі та у -перехопленні. Найбільш примітно, що y -перехоплення для зваженої лінійної регресії ближче до очікуваного значення нуля. Оскільки стандартне відхилення для сигналу, S _std, менше для менших концентрацій аналіту, C _STD, зважена лінійна регресія надає більше уваги цим стандартам, що дозволяє краще оцінити y -перехоплення.

Малюнок 5.14 PNG — Малюнок\(\PageIndex{1}\): Порівняння незважених і зважених нормальних калібрувальних кривих. \(\PageIndex{1}\)Докладніше про незважену лінійну регресію див. в Приклад та Приклад\(\PageIndex{4}\) для деталей зваженої лінійної регресії.

Рівняння для обчислення довірчих інтервалів для нахилу, y -перехоплення та концентрації аналіту при використанні зваженої лінійної регресії визначити не так просто, як для незваженої лінійної регресії [Bonate, P.J. Anal. Хім. 1993, 65, 1367—1372]. Однак довірчий інтервал для концентрації аналіта знаходиться на оптимальному значенні, коли сигнал аналіта знаходиться поблизу зважених центроїдів, y _c, калібрувальної кривої.

\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber\]