6.1: Властивості нормального розподілу

Математично нормальний розподіл визначається рівнянням

$$P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber$$

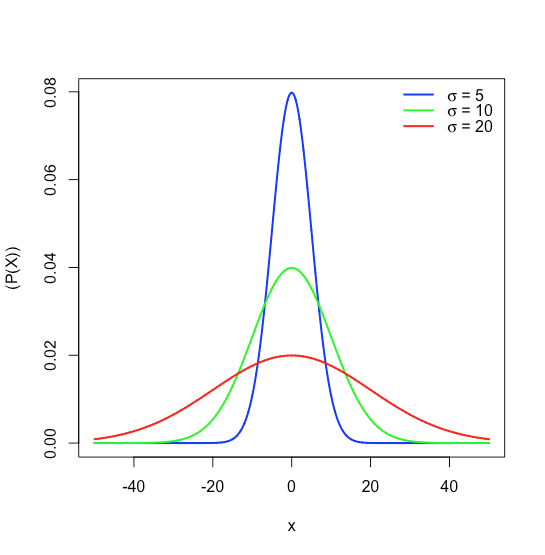
де$P(x)$ - ймовірність отримання результату$x$, від популяції з відомим середнім значенням$\mu$, і відомим стандартним відхиленням,$\sigma$. $\PageIndex{1}$На малюнку показані нормальні криві розподілу для$\mu = 0$ стандартних відхилень 5, 10 і 20.

Малюнок$\PageIndex{1}$: Три приклади нормальних кривих розподілу. Хоча на висоту і ширину впливають$\sigma$, площа під кожною кривою однакова.

Оскільки рівняння для нормального розподілу залежить виключно від середнього значення популяції та її стандартного відхилення, ймовірність того$\sigma$, що вибірка, взята з популяції, має значення між будь-якими двома довільними межами, однакова для всіх популяцій.$\mu$ Наприклад, малюнок$\PageIndex{2}$ показує, що 68,26% всіх зразків, взятих із нормально розподіленої сукупності, мають значення в межах діапазону$\mu \pm 1\sigma$, і лише 0,14% мають значення більше$\mu + 3\sigma$.

Рисунок$\PageIndex{2}$: Нормальна крива розподілу для$\mu = 0$ і$\sigma = 1$ показує площу під кривою для різних значень$z$ in$\mu \pm z \sigma$.

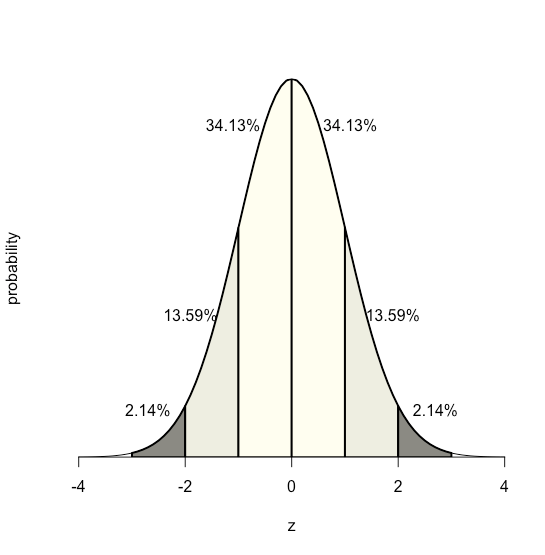
Ця особливість нормального розподілу - що площа під кривою однакова для всіх значень$\sigma$ —дозволяє нам створити таблицю ймовірностей (див. Додаток 1) на основі відносного відхилення між межею, x та середнім значенням,$\mu$.$z$

$$z = \frac {x - \mu} {\sigma} \nonumber$$

Значення$z$ дає площу під кривою між цією межею та найближчим хвостом розподілу, як показано на малюнку$\PageIndex{3}$.

Рисунок$\PageIndex{3}$: Нормальна крива розподілу для$\mu = 0$ і$\sigma = 1$ показ (зліва) області під кривою для$z = −1.5$ і (праворуч для$z = +0.5$.

Приклад$\PageIndex{1}$

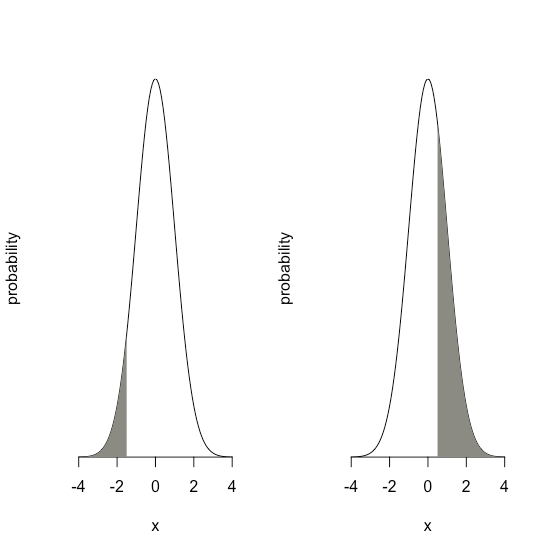
Припустимо, ми знаємо, що$\mu$ це 5.5833 ppb Pb і$\sigma$ це 0.0558 ppb Pb для конкретного стандартного довідкового матеріалу (SRM). Яка ймовірність того, що ми отримаємо результат, який перевищує 5.650 ppb, якщо проаналізувати одну випадкову вибірку, взяту з SRM?

Рішення

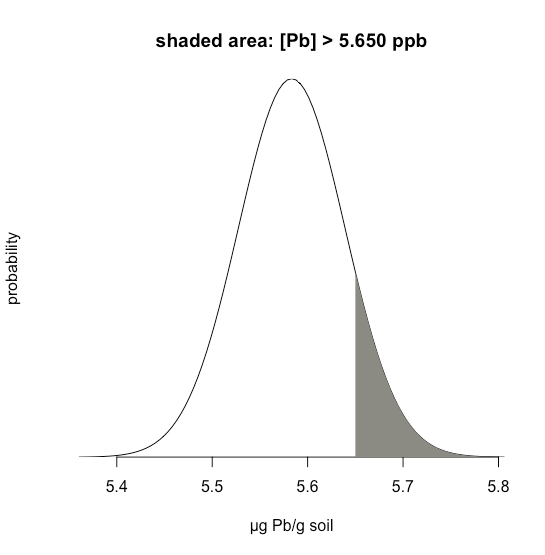
$\PageIndex{4}$На малюнку показана нормальна крива розподілу, задані значення 5,5833 ppb Pb для$\mu$ і 0,0558 ppb Pb$\sigma$. Затінена область на малюнках - це ймовірність отримання зразка з концентрацією Pb більше 5,650 проміле. Для визначення ймовірності спочатку обчислюємо$z$

$$z = \frac {x - \mu} {\sigma} = \frac {5.650 - 5.5833} {0.0558} = 1.195 \nonumber$$

Далі ми шукаємо ймовірність в Додатку 1 для цього значення$z$, яке є середнім значенням 0.1170 (for$z = 1.19$) і 0.1151 (для$z = 1.20$), або ймовірність 0.1160; таким чином, ми очікуємо, що 11,60% зразків нададуть результат більше 5.650 ppb.

Малюнок$\PageIndex{4}$: Нормальна крива розподілу кількості свинцю в стандартній довідці з$\mu = 5.5833$ ppb і$\sigma = 0.0558$ ppb. Затінена область показує ті результати, для яких концентрація свинцю перевищує 5.650 ppb.

Приклад$\PageIndex{2}$

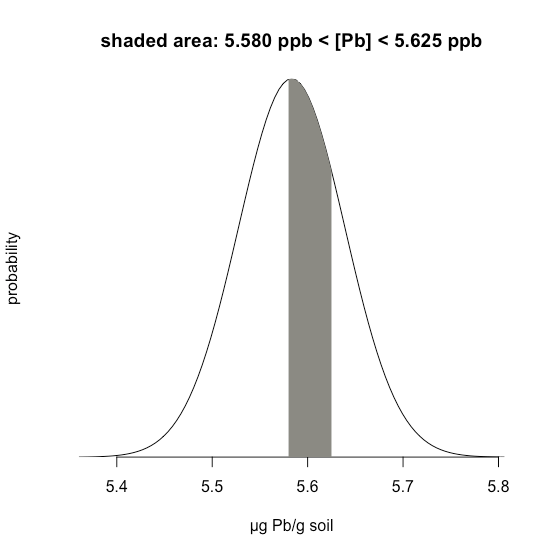
У прикладі$\PageIndex{1}$ розглядається одна межа — ймовірність того, що результат перевищує одне значення. Але що робити, якщо ми хочемо визначити ймовірність того, що зразок має між 5,580 г Pb і 5.625 г Pb?

Рішення

В даному випадку нас цікавить затінена область, показана на малюнку$\PageIndex{5}$. Спочатку розраховуємо$z$ для верхньої межі

$$z = \frac {5.625 - 5.5833} {0.0558} = 0.747 \nonumber$$

а потім розраховуємо$z$ для нижньої межі

$$z = \frac {5.580 - 5.5833} {0.0558} = -0.059 \nonumber$$

Потім ми шукаємо ймовірність у Додатку 1, що результат перевищить нашу верхню межу 5.625, що становить 0.2275, або 22,75%, і ймовірність того, що результат буде меншим за нашу нижню межу 5.580, що становить 0.4765, або 47,65%. Загальна незаштрихована площа становить 71,4% від загальної площі, тому затінена область відповідає ймовірності

$$100.00 - 22.75 - 47.65 = 100.00 - 71.40 = 29.6 \% \nonumber$$

Малюнок$\PageIndex{5}$: Нормальна крива розподілу кількості свинцю в стандартній довідці з$\mu = 5.5833$ ppb і$\sigma = 0.0558$ ppb. Затінена область показує ті результати, для яких концентрація свинцю становить більше 5,580 ppb і менше 5,625 ppb.