6.2: Інтервали довіри

У попередньому розділі ми навчилися прогнозувати ймовірність отримання того чи іншого результату, якщо наші дані нормально розподіляються з відомим\(\mu\) і відомим\(\sigma\). Наприклад, ми підрахували, що 11,60% зразків, взятих випадковим чином із стандартного еталонного матеріалу, матимуть концентрацію Pb більше 5,650 ppb, враховуючи 5,5833 ppb та a\(\sigma\) 0,0558 ppb.\(\mu\) По суті, ми визначили, від якої кількості стандартних відхилень становить 5,650,\(\mu\) і використали це для визначення ймовірності заданої стандартної площі при нормальній кривій розподілу.

Ми можемо поглянути на це по-іншому, задаючи наступне питання: Якщо ми збираємо одну вибірку навмання з популяції з відомим\(\mu\) і відомим\(\sigma\), в якому діапазоні значень ми можемо обґрунтовано очікувати, щоб знайти результат вибірки 95% часу? Перестановка рівняння

\[z = \frac {x - \mu} {\sigma} \nonumber\]

і рішення для\(x\) дарує

\[x = \mu \pm z \sigma = 5.5833 \pm (1.96)(0.0558) = 5.5833 \pm 0.1094 \nonumber\]

де a\(z\) 1,96 відповідає 95% площі під кривою; ми називаємо це 95% довірчим інтервалом для однієї вибірки.

Як правило, погано робити висновок з результату одного експерименту; натомість ми зазвичай збираємо кілька зразків і задаємо питання таким чином: якщо ми збираємо\(n\) випадкові зразки з популяції з відомим\(\mu\) і відомим\(\sigma\), в якому діапазоні значень ми могли б розумно розраховувати знайти середнє значення цих зразків 95% часу?

Ми можемо обґрунтовано очікувати, що стандартне відхилення для середнього значення декількох зразків менше, ніж стандартне відхилення для набору окремих зразків; насправді це так, і воно дається як

\[\sigma_{\bar{x}} = \frac {\sigma} {\sqrt{n}} \nonumber\]

де\(\frac {\sigma} {\sqrt{n}}\) називається стандартною похибкою середнього. Наприклад, якщо ми збираємо три зразки зі стандартного еталонного матеріалу, описаного вище, то ми очікуємо, що середнє значення для цих трьох зразків буде потрапляти в діапазон.

\[\bar{x} = \mu \pm z \sigma_{\bar{X}} = \mu \pm \frac {z \sigma} {\sqrt{n}} = 5.5833 \pm \frac{(1.96)(0.0558)} {\sqrt{3}} = 5.5833 \pm 0.0631 \nonumber\]

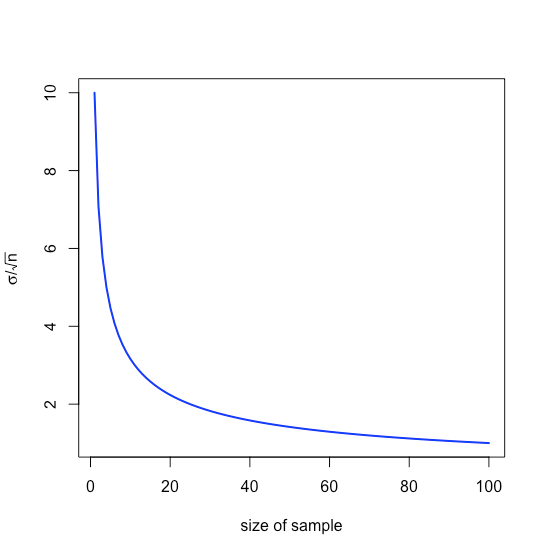
тобто\(\pm 0.0631\) ppb навколо\(\mu\), діапазон, який менший, ніж у\(\pm 0.1094\) ppb, коли ми аналізуємо окремі зразки. Зверніть увагу, що відносне значення для нас збільшення розміру вибірки зменшується зі\(n\) збільшенням через квадратний корінь, як показано на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Графік, що показує, як стандартна похибка середнього значення змінюється залежно від розміру вибірки. Значення для\(\sigma\) дорівнює 10.

Наше лікування досі передбачає, що ми знаємо\(\mu\) і\(\sigma\) для материнського населення, але ми рідко знаємо ці значення; натомість ми вивчаємо зразки, взяті з батьківської популяції,\(\bar{x}\) і задаємо наступне питання: Враховуючи середнє значення вибірки та її стандартне відхилення\(s\), що таке наше найкраща оцінка середнього чисельності населення\(\mu\), і його стандартного відхилення,\(\sigma\).

Щоб зробити цю оцінку, ми замінюємо стандартне відхилення населення\(\sigma\), на стандартне відхилення\(s\), для наших зразків, замінюємо середнє значення популяції\(\mu\), на середнє\(\bar{x}\), для наших зразків\(t\),\(z\) замінюємо на, де значення\(t\) залежить від кількість зразків,\(n\)

\[\bar{x} = \mu \pm \frac{ts}{\sqrt{n}} \nonumber\]

а потім переставити рівняння для вирішення\(\mu\).

\[\mu = \bar{x} \pm \frac {ts} {\sqrt{n}} \nonumber\]

Ми називаємо це довірчим інтервалом. Значення для\(t\) доступні в таблицях (див. Додаток 2) і залежать від рівня ймовірності\(\alpha\), де\((1 − \alpha) \times 100\) рівень довіри, і ступеня свободи\(n − 1\); зверніть увагу, що для будь-якого рівня ймовірності,\(t \longrightarrow z\) як\(n \longrightarrow \infty\).

Потрібно приділити особливу увагу тому, що означає цей довірчий інтервал і що він не означає:

• Це не означає, що існує 95% ймовірність того, що середнє значення населення знаходиться в діапазоні,\(\mu = \bar{x} \pm ts\) оскільки наші вимірювання можуть бути упередженими або нормальний розподіл може бути неприйнятним для нашої системи.
• Це забезпечує нашу найкращу оцінку середнього рівня популяції,\(\mu\) враховуючи наш аналіз\(n\) зразків, взятих випадковим чином з материнської популяції; однак інша вибірка дасть інший довірчий інтервал і, отже, іншу оцінку для\(\mu\).