9.3: Титрування комплексоутворення
- Page ID
- 24851
Найбільш ранніми прикладами титрування комплексоутворення метал-ліганд є визначення Лібіха у 1850-х роках ціаніду та хлориду, що використовують відповідно Ag + та Hg 2 + як титрант. Практичні аналітичні застосування комплексоутворення титриметрії розвивалися повільно, оскільки багато металів і лігандів утворюють низку комплексів метал-ліганд. Титрування Лібіха CN - з Ag + було успішним, оскільки вони утворюють єдиний стабільний комплекс\(\text{Ag(CN)}_2^-\), що призводить до єдиної, легко ідентифікованої кінцевої точки. Інші метало-лігандні комплекси, такі як\(\text{CdI}_4^{2-}\), не є аналітично корисними, оскільки вони утворюють низку комплексів метал-ліганд (CDi +, CDi 2 (aq)\(\text{CdI}_3^-\) та\(\text{CdI}_4^{2-}\)), які створюють послідовність погано визначених кінцевих точок.
Нагадаємо, що крива титрування кислота-основа для дипротової слабкої кислоти має єдину кінцеву точку, якщо її два значення K a недостатньо різні. Див. Малюнок 9.2.6 для прикладу.
У 1945 році Шварценбах ввів амінокарбонові кислоти як мультидентатні ліганди. Найбільш широко використовувані з цих нових лігандів - етилендіамінтетраоцтова кислота або ЕДТА - утворює сильний комплекс 1:1 з багатьма іонами металів. Наявність ліганду, що дає єдину, легко ідентифіковану кінцеву точку, зробила комплексоутворення титриметрії практичним аналітичним методом.
Хімія та властивості ЕДТА
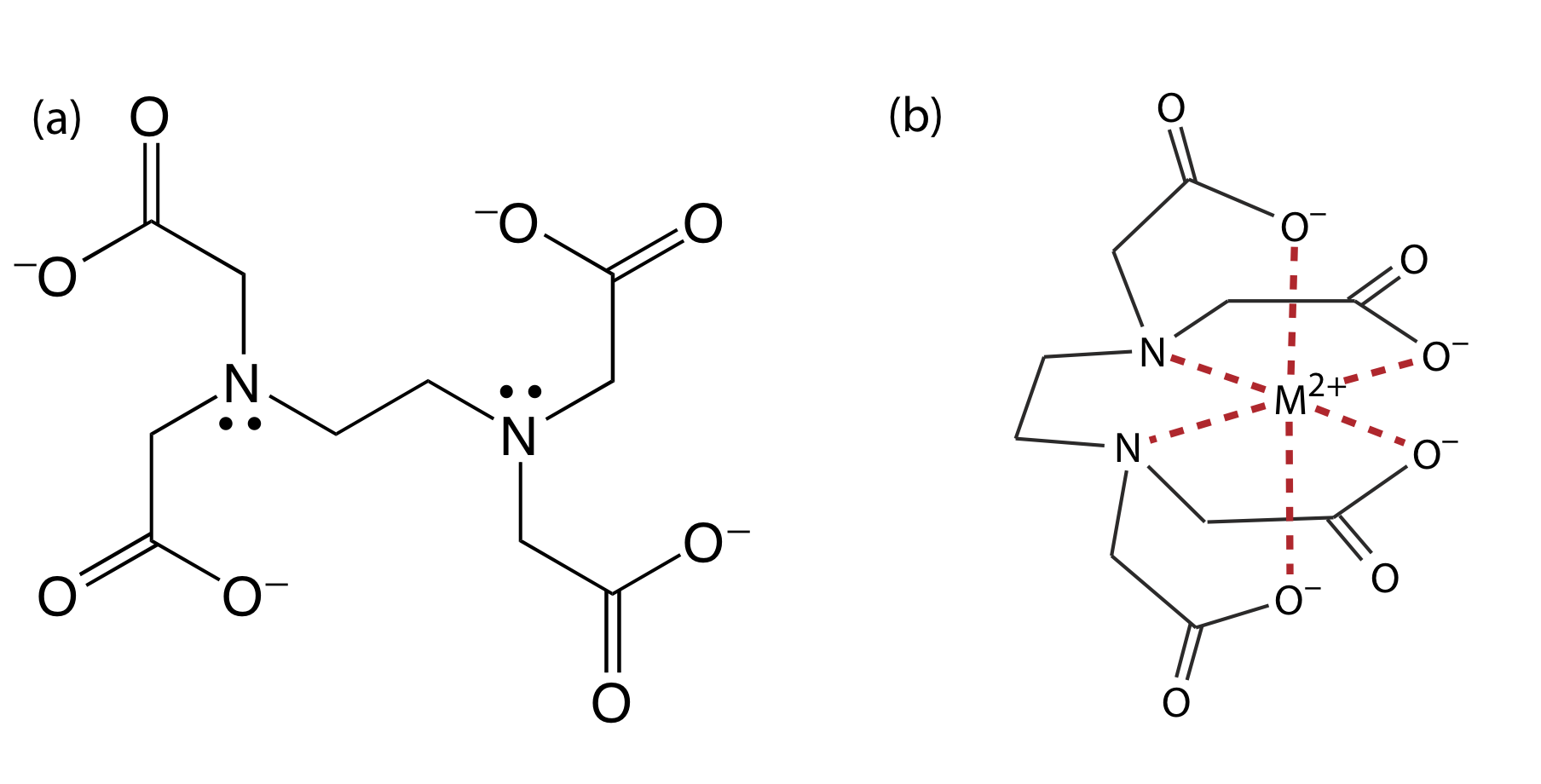
Етилендіамінтетраоцтова кислота, або ЕДТА, являє собою амінокарбонову кислоту. ЕДТА, структура якої показана на малюнку Template:index a в повністю депротонованій формі, являє собою кислоту Льюїса з шістьма місцями зв'язування - чотирма негативно зарядженими карбоксилатними групами та двома третинними аміногрупами - які можуть пожертвувати до шести пар електронів іону металу. Отриманий комплекс метал-ліганд, в якому ЕДТА утворює навколо іона металу подібну до клітки структуру (рис. Template:index b), є дуже стабільним. Фактична кількість координаційних ділянок залежить від розміру іона металу, проте всі комплекси метал—ЕДТА мають стехіометрію 1:1.
Константи формування метал-ЕДТА
Для ілюстрації формування комплексу метал—ЕДТА розглянемо реакцію між Cd 2 + та EDTA
де Y 4— є скороченим позначенням для повністю депротонованої форми ЕДТА, показаної на малюнку Template:index a.
великий, його положення рівноваги лежить далеко праворуч. Константи формування для інших комплексів метал—ЕДТА наведено у Додатку 12.
ЕДТА є слабкою кислотою
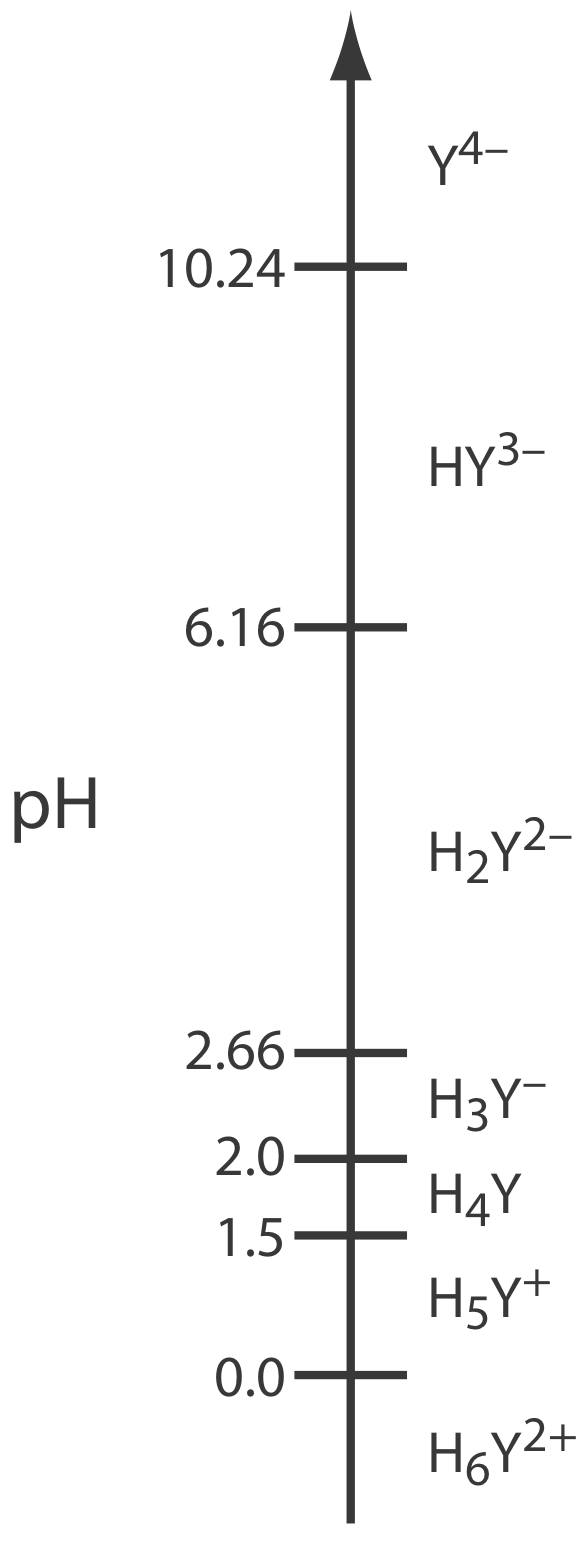
Крім своїх властивостей як ліганда, ЕДТА є ще й слабкою кислотою. Повністю протонована форма ЕДТА, H 6 Y 2+, являє собою гексапротонну слабку кислоту з послідовними значеннями p K a
\[\mathrm{p} K_\text{a1}=0.0 \quad \mathrm{p} K_\text{a2}=1.5 \quad \mathrm{p} K_\text{a3}=2.0 \nonumber\]
\[\mathrm{p} K_\text{a4}=2.66 \quad \mathrm{p} K_\text{a5}=6.16 \quad \mathrm{p} K_\text{a6}=10.24 \nonumber\]
Перші чотири значення призначені для протонів карбонової кислоти, а останні два значення - для протонів амонію. На малюнку Template:index показано діаграму сходів для ЕДТА. Специфічна форма ЕДТА в реакції\ ref {9.1} є переважаючим видом лише тоді, коли рН є більш основним, ніж 10,24.
Умовні константи формування метал—ліганд
Константа формування для CdY 2— у рівнянні\ ref {9.2} передбачає, що EDTA присутній як Y 4—. Тому що ЕДТА має багато форм, коли ми готуємо розчин ЕДТА, ми знаємо його загальна концентрація, С ЕДТА, а не концентрація конкретної форми, такі як Y 4—. Щоб використовувати Equation\ ref {9.2}, нам потрібно переписати його в терміні C EDTA.
При будь-якому рН баланс маси на ЕДТА вимагає, щоб його загальна концентрація дорівнювала комбінованим концентраціям кожної з його форм.
\[C_{\mathrm{EDTA}}=\left[\mathrm{H}_{6} \mathrm{Y}^{2+}\right]+\left[\mathrm{H}_{5} \mathrm{Y}^{+}\right]+\left[\mathrm{H}_{4} \mathrm{Y}\right]+\left[\mathrm{H}_{3} \mathrm{Y}^-\right]+\left[\mathrm{H}_{2} \mathrm{Y}^{2-}\right]+\left[\mathrm{HY}^{3-}\right]+\left[\mathrm{Y}^{4-}\right] \nonumber\]
Щоб виправити константу утворення для кислотно-основи властивостей ЕДТА, нам потрібно обчислити частку ЕДТА\(\alpha_{\text{Y}^{4-}}\), яка присутня як Y 4—.
\[\alpha_{\text{Y}^{4-}}=\frac{\left[\text{Y}^{4-}\right]}{C_\text{EDTA}} \label{9.3}\]
Таблиця Template:index містить значення\(\alpha_{\text{Y}^{4-}}\) для вибраних рівнів рН. Розв'язування рівняння\ ref {9.3} для [Y 4—] та підстановка на рівняння\ ref {9.2} для константи формування CdY 2—
\[K_{\mathrm{f}}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] (\alpha_{\mathrm{Y}^{4-}}) C_{\mathrm{EDTA}}} \nonumber\]
і перестановка дає
де\(K_f^{\prime}\) - pH-залежна умовна константа освіти. Як показано в таблиці Template:index, константа умовного формування для CdY 2— стає меншою, а комплекс стає менш стабільним при більш кислих рН.
| рН | \(\alpha_{\text{Y}^{4-}}\) | рН | \(\alpha_{\text{Y}^{4-}}\) |
|---|---|---|---|
| 1 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(1.94 \times 10^{-18}\) | 8 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(5.68 \times 10^{-3}\) |
| 2 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(3.47 \times 10^{-14}\) | 9 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(5.47 \times 10^{-2}\) |
| 3 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(2.66 \times 10^{-11}\) | 10 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">0.367 |
| 4 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(3.80 \times 10^{-9}\) | 11 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">0.853 |
| 5 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(3.73 \times 10^{-7}\) | 12 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">0.983 |
| 6 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(2.37 \times 10^{-5}\) | 13 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">0.988 |
| 7 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">\(5.06 \times 10^{-4}\) | 14 | \ (\ альфа_ {\ текст {Y} ^ {4-}}\) ">1.00 |
| рН | \(\text{K}_f^{\prime}\) | рН | \(\text{K}_f^{\prime}\) |
|---|---|---|---|
| 1 | \ (\ текст {K} _f^ {\ прайм}\) ">\(5.6 \times 10^{-2}\) | 8 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.6 \times 10^{14}\) |
| 2 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.0 \times 10^{3}\) | 9 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.6 \times 10^{15}\) |
| 3 | \ (\ текст {K} _f^ {\ прайм}\) ">\(7.7 \times 10^{5}\) | 10 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.1 \times 10^{16}\) |
| 4 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.1 \times 10^{8}\) | 11 | \ (\ текст {K} _f^ {\ прайм}\) ">\(2.5 \times 10^{16}\) |
| 5 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.1 \times 10^{10}\) | 12 | \ (\ текст {K} _f^ {\ прайм}\) ">\(2.9 \times 10^{16}\) |
| 6 | \ (\ текст {K} _f^ {\ прайм}\) ">\(6.9 \times 10^{11}\) | 13 | \ (\ текст {K} _f^ {\ прайм}\) ">\(2.9 \times 10^{16}\) |
| 7 | \ (\ текст {K} _f^ {\ прайм}\) ">\(1.5 \times 10^{13}\) | 14 | \ (\ текст {K} _f^ {\ прайм}\) ">\(2.9 \times 10^{16}\) |
ЕДТА конкурує з іншими лігандами
Для підтримки постійного рН під час титрування комплексоутворення ми зазвичай додаємо буферний агент. Якщо одним з компонентів буфера є ліганд, який зв'язується з Cd 2 +, то ЕДТА повинна конкурувати з лігандом для Cd 2 +. Наприклад,\(\text{NH}_4^+ / \text{NH}_3\) буфер включає NH 3, який утворює кілька стабільних комплексів Cd 2 + —NH 3. Оскільки ЕДТА утворює більш сильний комплекс з Cd 2 +, ніж NH 3, він витісняє NH 3; однак стабільність комплексу Cd 2 + —EDTA зменшується.
Ми можемо враховувати ефект допоміжного комплексоутворювача, такого як NH 3, так само, як ми враховували ефект рН. Перед додаванням ЕДТА баланс маси на Cd 2 +, C Cd, дорівнює
\[C_{\mathrm{Cd}} = \left[\mathrm{Cd}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{2}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{4}^{2+}\right] \nonumber\]
і частка незакомплексованого Cd 2 +,\(\alpha_{Cd^{2+}}\), дорівнює
\[\alpha_{\mathrm{Cd}^{2+}}=\frac{\left[\mathrm{Cd}^{2+}\right]}{C_{\mathrm{Cd}}} \label{9.5}\]
Значення\(\alpha_{\mathrm{Cd}^{2+}}\) залежить від концентрації NH 3. Контраст це з\(\alpha_{\text{Y}^{4-}}\), який залежить від рН.
Розв'язування рівняння\ ref {9.5} для [Cd 2+] і підстановка в рівняння\ ref {9.4} дає
\[K_{f}^{\prime}=K_{f} \times \alpha_{Y^{4-}} = \frac {[\text{CdY}^{2-}]} {\alpha_{\text{Cd}^{2+}} C_\text{Cd} C_\text{EDTA}} \nonumber\]
Оскільки концентрація NH 3 в буфері по суті є постійною, ми можемо переписати це рівняння
дати константу умовного формування\(K_f^{\prime \prime}\), що враховує як рН, так і концентрацію допоміжного комплексоутворювача. Таблиця Template:index містить значення\(\alpha_{\text{M}^{2+}}\) для декількох іонів металів, коли NH 3 є комплексоутворювачем.
| [NH 3] (М) | \(\alpha_{\text{Ca}^{2+}}\) | \(\alpha_{\text{Cd}^{2+}}\) | \(\alpha_{\text{Co}^{2+}}\) | \(\alpha_{\text{Cu}^{2+}}\) | \(\alpha_{\text{Mg}^{2+}}\) | \(\alpha_{\text{Ni}^{2+}}\) | \(\alpha_{\text{Zn}^{2+}}\) |
|---|---|---|---|---|---|---|---|
| 1 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(5.50 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.09 \times 10^{-8}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.00 \times 10^{-6}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.79 \times 10^{-14}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.76 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.20 \times 10^{-10}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.95 \times 10^{-10}\) |
| 0.5 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(7.36 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.05 \times 10^{-6}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(2.22 \times 10^{-5}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.86 \times 10^{-13}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(4.13 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.44 \times 10^{-8}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.27 \times 10^{-9}\) |
| 0.1 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.39 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.51 \times 10^{-4}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.64 \times 10^{-3}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(4.63 \times 10^{-10}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(8.48 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(5.12 \times 10^{-5}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.68 \times 10^{-6}\) |
| 0,05 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.69 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(2.72 \times 10^{-3}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.54 \times 10^{-2}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(7.17 \times 10^{-9}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.22 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.37 \times 10^{-4}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(5.45 \times 10^{-5}\) |
| 0,01 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.94 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(8.81 \times 10^{-2}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.55 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.22 \times 10^{-6}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.84 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(4.32 \times 10^{-2}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.82 \times 10^{-2}\) |
| 0,005 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.97 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(2.27 \times 10^{-1}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(5.68 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(3.62 \times 10^{-5}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.92 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.36 \times 10^{-1}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(1.27 \times 10^{-1}\) |
| 0,001 | \ (\ alpha_ {\ text {Ca} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.99 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cd} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(6.09 \times 10^{-1}\) | \ (\ alpha_ {\ text {Co} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(8.84 \times 10^{-1}\) | \ (\ alpha_ {\ text {Cu} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(4.15 \times 10^{-4}\) | \ (\ alpha_ {\ text {Mg} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(9.98 \times 10^{-1}\) | \ (\ alpha_ {\ text {Ni} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(5.76 \times 10^{-1}\) | \ (\ alpha_ {\ text {Zn} ^ {2+}}\)» style="вертикальне вирівнювання: середина; ">\(7.48 \times 10^{-1}\) |
Комплексометричні криві титрування ЕДТА
Тепер, коли ми знаємо щось про хімічні властивості ЕДТА, ми готові оцінити його корисність як титрант. Для цього нам потрібно знати форму комплексометричної кривої титрування. У розділі 9.2 ми дізналися, що крива титрування кислотно-основа показує, як змінюється рН титранду, коли ми додаємо титрант. Аналогічний результат титрування комплексоутворення показує зміну pM, де M - концентрація іонів металу, як функція об'єму ЕДТА. У цьому розділі ми дізнаємося, як розрахувати криву титрування, використовуючи розрахунки рівноваги з глави 6. Ми також навчимося накидати гарне наближення будь-якої кривої титрування комплексоутворення, використовуючи обмежену кількість простих обчислень.
пМ = —журнал [М 2+]
Розрахунок кривої титрування
Розрахуємо криву титрування для 50,0 мл\(5.00 \times 10^{-3}\) M Cd 2 +, використовуючи титрант 0,0100 М ЕДТА. Крім того, припустимо, що титранд буферується до рН 10 за допомогою буфера, який становить 0,0100 М у NH 3.
Оскільки рН становить 10, деякі з ЕДТА присутній у формах, відмінних від Y 4—. Крім того, EDTA буде конкурувати з NH 3 за Cd 2 +. Отже, для оцінки кривої титрування спочатку потрібно обчислити константу умовного формування для CdY 2—. З таблиці Template:index та таблиці Template:index ми знаходимо, що\(\alpha_{\text{Y}^{4-}}\) це 0,367 при рН 10, і\(\alpha_{\text{Cd}^{2+}}\) це 0,0881, коли концентрація NH 3 становить 0,0100 М. Використовуючи ці значення, константа умовного формування дорівнює
\[K_{f}^{\prime \prime}=K_{f} \times \alpha_{\text{Y}^{4-}} \times \alpha_{\text{Cd}^{2+}}=\left(2.9 \times 10^{16}\right)(0.367)(0.0881)=9.4 \times 10^{14} \nonumber\]
Оскільки\(K_f^{\prime \prime}\) він такий великий, ми можемо лікувати реакцію титрування
\[\mathrm{Cd}^{2+}(a q)+\mathrm{Y}^{4-}(a q) \longrightarrow \mathrm{CdY}^{2-}(a q) \nonumber\]
ніби вона переходить до завершення.
Наступне завдання - визначити обсяг ЕДТА, необхідний для досягнення точки еквівалентності. У точці еквівалентності ми знаємо, що додані родимки ЕДТА повинні дорівнювати молям Cd 2 + в нашому зразку; таким чином
\[\operatorname{mol} \mathrm{EDTA}=M_{\mathrm{EDTA}} \times V_{\mathrm{EDTA}}=M_{\mathrm{Cd}} \times V_{\mathrm{Cd}}=\mathrm{mol} \ \mathrm{Cd}^{2+} \nonumber\]
Підставляючи в відомі значення, виявляємо, що для цього потрібно
\[V_{eq}=V_{\mathrm{EDTA}}=\frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{0.0100 \ \mathrm{M}}=25.0 \ \mathrm{mL} \nonumber\]
ЕДТА досягти точки еквівалентності.
Перед точкою еквівалентності Cd 2+ присутній в надлишку і pCd визначається концентрацією не прореагував Cd 2 +. Оскільки не всі невідреагували Cd 2 + є вільними - деякі комплексні з NH 3 - ми повинні враховувати наявність NH 3. Наприклад, після додавання 5,0 мл ЕДТА загальна концентрація Cd 2 + становить
\[C_{\mathrm{Cd}} = \frac {(\text{mol Cd}^{2+})_\text{initial} - (\text{mol EDTA})_\text{added}} {\text{total volume}} = \frac {M_\text{Cd}V_\text{Cd} - M_\text{EDTA}V_\text{EDTA}} {V_\text{Cd} + V_\text{EDTA}} \nonumber\]
\[C_{\mathrm{Cd}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})-(0.0100 \ \mathrm{M})(5.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+5.0 \ \mathrm{mL}} \nonumber\]
\[C_{\mathrm{Cd}}=3.64 \times 10^{-3} \ \mathrm{M} \nonumber\]
Для розрахунку концентрації вільного Cd 2 + використовуємо Equation\ ref {9.5}
\[\left[\mathrm{Cd}^{2+}\right]=\alpha_{\mathrm{Cd}^{2+}} \times C_{\mathrm{Cd}}=(0.0881)\left(3.64 \times 10^{-3} \ \mathrm{M}\right)=3.21 \times 10^{-4} \ \mathrm{M} \nonumber\]
що дає ПКД
\[\mathrm{pCd}=-\log \left[\mathrm{Cd}^{2+}\right]=-\log \left(3.21 \times 10^{-4}\right)=3.49 \nonumber\]
У точці еквівалентності всі Cd 2 + спочатку в титранді тепер присутні як CDy 2—. Концентрація Cd 2 +, отже, визначається дисоціацією комплексу CdY 2—. Спочатку обчислюємо концентрацію CdY 2—.
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(\mathrm{mol} \ \mathrm{Cd}^{2+}\right)_{\mathrm{initial}}}{\text { total volume }} = \frac {M_\text{Cd}V_\text{Cd}} {V_\text{Cd} + V_\text{EDTA}} \nonumber\]
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}}=3.33 \times 10^{-3} \ \mathrm{M} \nonumber\]
Далі вирішуємо для концентрації Cd 2 + в рівновазі з CdY 2—.
\[K_{\mathrm{f}}^{\prime \prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{Cd}} C_{\mathrm{EDTA}}}=\frac{3.33 \times 10^{-3}-x}{(x)(x)}=9.5 \times 10^{14} \nonumber\]
\[x=C_{\mathrm{Cd}}=1.87 \times 10^{-9} \ \mathrm{M} \nonumber\]
Розраховуючи, що [CdY 2—] в точці еквівалентності дорівнює\(3.33 \times 10^{-3}\) M, ми припустили, що реакція між Cd 2 + і EDTA пішла до завершення. Тут ми дозволяємо системі розслабитися назад до рівноваги, збільшуючи C Cd і C EDTA від 0 до х, і зменшуючи концентрацію CdY 2— на x.
Ще раз, щоб знайти концентрацію некомплексного Cd, ми повинні враховувати наявність NH 3; таким чином
\[\left[\mathrm{Cd}^{2+}\right]=\alpha_{\mathrm{Cd}^{2+}} \times C_{\mathrm{Cd}}=(0.0881)\left(1.87 \times 10^{-9} \ \mathrm{M}\right)=1.64 \times 10^{-10} \ \mathrm{M} \nonumber\]
і pCd становить 9,78 в точці еквівалентності.
Після точки еквівалентності ЕДТА перевищує і концентрація Cd 2 + визначається дисоціацією комплексу CdY 2—. По-перше, ми обчислюємо концентрації CdY 2— і не прореагували ЕДТА. Наприклад, після додавання 30,0 мл ЕДТА концентрація CdY 2— становить
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(\mathrm{mol} \mathrm{Cd}^{2+}\right)_{\mathrm{initial}}}{\text { total volume }} = \frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{V_{\mathrm{Cd}}+V_{\mathrm{EDTA}}} \nonumber\]
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.0 \ \mathrm{mL}}=3.12 \times 10^{-3} \ \mathrm{M} \nonumber\]
і концентрація ЕДТА
\[C_{\mathrm{EDTA}} = \frac {(\text{mol EDTA})_\text{added} - (\text{mol Cd}^{2+})_\text{initial}} {\text{total volume}} = \frac{M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{V_{\mathrm{Cd}}+V_{\mathrm{EDTA}}} \nonumber\]
\[C_{\text{EDTA}} = \frac {(0.0100 \text{ M})(30.0 \text{ mL}) - (5.00 \times 10^{-3} \text{ M})(50.0 \text{ mL})} {50.0 \text{ mL} + 30.0 \text{ mL}} \nonumber\]
\[C_{\mathrm{EDTA}}=6.25 \times 10^{-4} \ \mathrm{M} \nonumber\]
Підстановка в рівняння\ ref {9.6} і розв'язування для [Cd 2 +] дає
\[\frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{Cd}} C_{\mathrm{EDTA}}} = \frac{3.12 \times 10^{-3} \ \mathrm{M}}{C_{\mathrm{Cd}}\left(6.25 \times 10^{-4} \ \mathrm{M}\right)} = 9.5 \times 10^{14} \nonumber\]
\[C_{\text{Cd}} = 5.27 \times 10^{-15} \text{ M} \nonumber\]
\[ \left[ \text{Cd}^{2+} \right] = \alpha_{\text{Cd}^{2+}} \times C_{\text{Cd}} = (0.0881)(5.27 \times 10^{-15} \text{ M}) = 4.64 \times 10^{-16} \text{ M} \nonumber\]
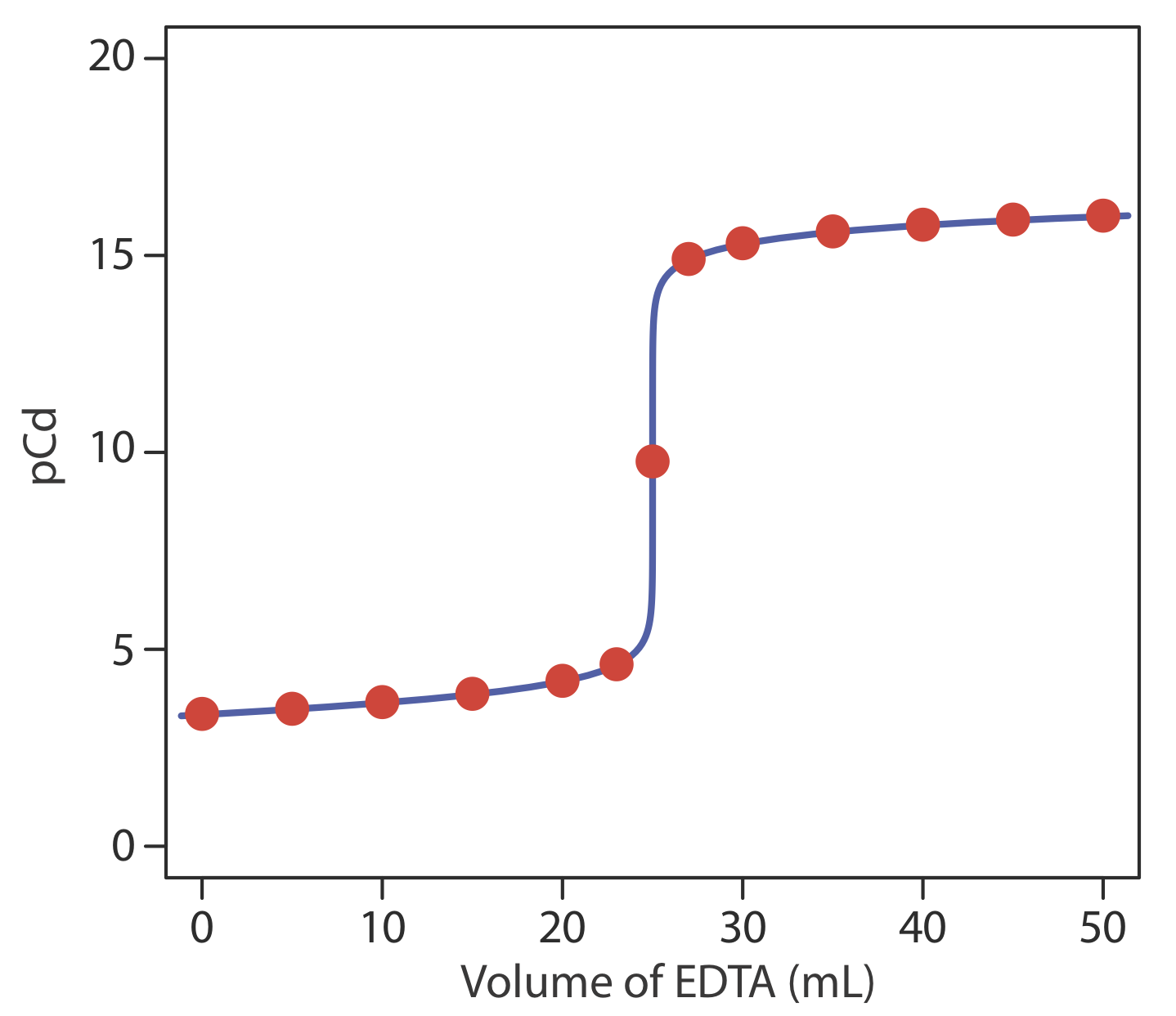
ПКД 15,33. Таблиця Template:index та рисунок Template:index показують додаткові результати для цього титрування.
Після точки рівноваги ми знаємо рівноважні концентрації CdY 2 - і ЕДТА у всіх його формах, C EDTA. Ми можемо вирішити для C Cd використовуючи,\(K_f^{\prime \prime}\) а потім обчислити [Cd 2 +] використовуючи\(\alpha_{\text{Cd}^{2+}}\). Оскільки ми використовували ту саму константу умовного формування\(K_f^{\prime \prime}\), для інших розрахунків у цьому розділі, цей підхід також використовується тут. Існує другий метод обчислення [Cd 2 +] після точки еквівалентності. Оскільки обчислення використовує лише [CDy 2 -] та C EDTA, ми можемо використовувати\(K_f^{\prime}\) замість\(K_f^{\prime \prime}\); таким чином
\[\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\alpha_{\mathrm{Y}^{4-}} \times K_{\mathrm{f}} \nonumber\]
\[\frac{3.13 \times 10^{-3} \ \mathrm{M}}{\left[\mathrm{Cd}^{2+}\right]\left(6.25 \times 10^{-4}\right)}=(0.367)\left(2.9 \times 10^{16}\right) \nonumber\]
Розв'язування дає [Cd 2 +] =\(4.71 \times 10^{-16}\) M і pCd 15.33. Ми будемо використовувати цей підхід, коли навчимося малювати комплексометричну криву титрування.
| Обсяг ЕДТА (мл) | PcD | Обсяг ЕДТА (мл) | PcD |
|---|---|---|---|
| 0.00 | 3.36 | 27.0 | 14,95 |
| 5.00 | 3.49 | 30.0 | 15.33 |
| 10.0 | 3.66 | 35.0 | 15.61 |
| 15,0 | 3.87 | 40.0 | 15.76 |
| 20.0 | 4.20 | 45.0 | 15.86 |
| 23,0 | 4.62 | 50.0 | 15.94 |
| 25.0 | 9.78 |
Обчисліть криві титрування для титрування 50,0 мл\(5.00 \times 10^{-3}\) M Cd 2 + з 0,0100 М ЕДТА (а) при рН 10 і (b) при рН 7. Ні титрування не включає допоміжний комплексоутворюючий агент. Порівняйте свої результати з рисунком Template:index і прокоментуйте вплив pH на титрування Cd 2 + з ЕДТА.
- Відповідь
-
Почнемо з розрахунків при рН 10, де деякі з ЕДТА присутній у формах, відмінних від Y 4—. Отже, для оцінки кривої титрування нам потрібна константа умовного формування для CdY 2—, яка з таблиці Template:index є\(K_f^{\prime} = 1.1 \times 10^{16}\). Відзначимо, що константа умовного формування більше при відсутності допоміжного комплексообразователя.
Точка еквівалентності титрування вимагає
\[V_{e q}=V_{\mathrm{EDTA}}=\frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{(0.0100 \ \mathrm{M})}=25.0 \ \mathrm{mL} \nonumber\]
ЕДТА.
Перед точкою еквівалентності Cd 2+ присутній в надлишку і pCd визначається концентрацією не прореагував Cd 2 +. Наприклад, після додавання 5,00 мл ЕДТА загальна концентрація Cd 2 + становить
\[\left[\mathrm{Cd}^{2+}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})-(0.0100 \ \mathrm{M})(5.00 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+5.00 \ \mathrm{mL}} \nonumber\]
який дає [Cd 2 +] як\(3.64 \times 10^{-3}\) і PcD як 2.43.
У точці еквівалентності всі Cd 2 + спочатку в титранді тепер присутні як CDy 2—. Концентрація Cd 2 +, отже, визначається дисоціацією комплексу CdY 2—. Спочатку обчислюємо концентрацію CdY 2—.
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.00 \ \mathrm{mL}}=3.33 \times 10^{-3} \ \mathrm{M} \nonumber\]
Далі вирішуємо для концентрації Cd 2 + в рівновазі з CdY 2—.
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\frac{3.33 \times 10^{-3}-x}{(x)(x)}=1.1 \times 10^{16} \nonumber\]
Розв'язування дає [Cd 2 +] як\(5.50 \times 10^{-10}\) M або pCd 9,26 в точці еквівалентності.
Після точки еквівалентності ЕДТА перевищує і концентрація Cd 2 + визначається дисоціацією комплексу CdY 2—. По-перше, ми обчислюємо концентрації CdY 2— і не прореагували ЕДТА. Наприклад, після додавання 30,0 мл ЕДТА
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.00 \ \mathrm{mL}}=3.12 \times 10^{-3} \ \mathrm{M} \nonumber\]
\[C_{\mathrm{EDTA}}=\frac{(0.0100 \ \mathrm{M})(30.00 \ \mathrm{mL})-\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.00 \ \mathrm{mL}} \nonumber\]
\[C_{\mathrm{EDTA}}=6.25 \times 10^{-4} \ \mathrm{M} \nonumber\]
Підстановка в рівняння константи умовного формування
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\frac{3.12 \times 10^{-3} \ \mathrm{M}}{(\mathrm{x})\left(6.25 \times 10^{-4} \ \mathrm{M}\right)}=1.1 \times 10^{16} \nonumber\]
і рішення для [Cd 2 +] дає\(4.54 \times 10^{-16}\) M або pCd 15.34.
Обчислення при рН 7 ідентичні, за винятком константи умовного формування для CdY 2—\(1.5 \times 10^{13}\) замість\(1.1 \times 10^{16}\). Наступна таблиця узагальнює результати цих двох титрувань, а також результати таблиці Template:index для титрування Cd 2+ при рН 10 у присутності 0,0100 M NH 3 як допоміжного комплексоутворювача.
Обсяг ЕДТА (мл)
PcD при рН 10
PcD при рН 10 Вт/0,0100 М NH 3
PcD при рН 7
0 2.30
3.36
2.30
5.00
2.43
3.49
2.43
10.0 2.60
3.66
2.60
15,0 2.81
3.87
2.81
20.0 3.15
4.20
3.15
23,0 3.56
4.62
3.56
25.0 9.26
9.77
7.83
27.0 14.94 14,95 12.08
30.0 15.34 15.33 12.48 35.0 15.61 15.61 12.78 40.0 15.76 15.76 12,95 45.0 15.86 15.86 13.08 50.0 15.94 15.94 13.18 Вивчення цих результатів дозволяє зробити кілька висновків. По-перше, при відсутності допоміжного комплексообразователя крива титрування перед точкою еквівалентності не залежить від рН (порівняйте стовпці 2 і 4). По-друге, для будь-якого рН крива титрування після точки еквівалентності однакова незалежно від того, чи присутній допоміжний комплексоутворювач (порівняйте стовпці 2 і 3). По-третє, найбільша зміна рН через точку еквівалентності відбувається при більш високих рН і при відсутності допоміжного комплексообразователя. Наприклад, від 23,0 мл до 27,0 мл ЕДТА зміна ПКД становить 11,38 при рН 10, 10,33 при рН 10 в присутності 0,0100 М NH 3 і 8,52 при рН 7.
Ескіз кривої титрування ЕДТА
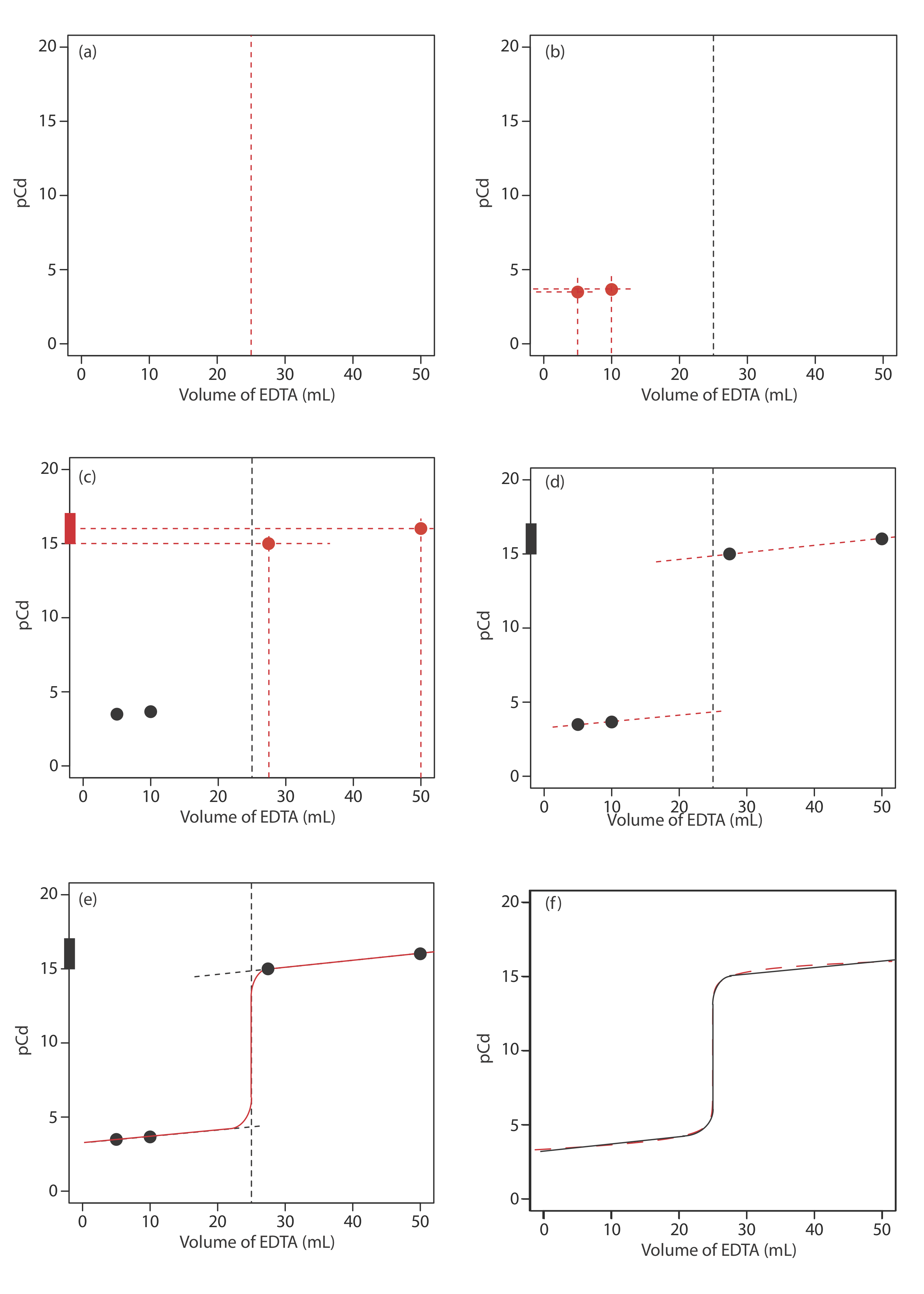
Щоб оцінити зв'язок між точкою еквівалентності титрування та її кінцевою точкою, нам потрібно побудувати лише розумне наближення точної кривої титрування. У цьому розділі ми продемонструємо простий метод ескізу кривої титрування комплексоутворення. Наша мета - швидко намалювати криву титрування, використовуючи якомога менше розрахунків. Давайте використаємо титрування 50,0 мл\(5.00 \times 10^{-3}\) M Cd 2 + з 0,0100 M EDTA в присутності 0,0100 M NH 3, щоб проілюструвати наш підхід. Це той самий приклад, який ми використовували при розробці розрахунків для кривої титрування комплексоутворення. Ви можете переглянути результати цього розрахунку у таблиці Template:index та на малюнку Template:index.
Почнемо з розрахунку об'єму точки еквівалентності титрування, який, як ми визначили раніше, становить 25,0 мл. Далі ми малюємо наші осі, розмістивши pcD на осі y і об'єм титранта на осі x. Щоб вказати об'єм точки еквівалентності, проводимо вертикальну лінію, яка перетинає вісь x на 25,0 мл ЕДТА. Рисунок Template:index a показує результат першого кроку нашого ескізу.
Перед точкою еквівалентності Cd 2 + присутній в надлишку і pCd визначається концентрацією не прореагував Cd 2 +. Оскільки не всі невідреагували Cd 2 + є вільними - деякі комплексні з NH 3 - ми повинні враховувати наявність NH 3. Розрахунки нехитрі, як ми бачили раніше. На малюнку Template:index b показано PCD після додавання 5,00 мл та 10,0 мл ЕДТА.
Третім кроком ескізу нашої кривої титрування є додавання двох точок після точки еквівалентності. Тут концентрація Cd 2 + контролюється дисоціацією комплексу Cd 2 + —EDTA. Починаючи з константи умовного формування
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}} = \alpha_{\text{Y}^{4-}} \times K_{f}=(0.367)\left(2.9 \times 10^{16}\right)=1.1 \times 10^{16} \nonumber\]
беремо колоду з кожного боку і переставляємо, приїжджаючи на
\[\begin{array}{c}{\log K_{f}^{\prime}=-\log \left[\mathrm{Cd}^{2+}\right]+\log \frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{EDTA}}}} \\ {\mathrm{pCd}=\log K_{f}^{\prime}+\log \frac{C_{\mathrm{EDTA}}}{\left[\mathrm{CdY}^{2-}]\right.}}\end{array} \nonumber\]
Нагадаємо, що ми можемо використовувати або з двох наших можливих констант умовного формування\(K_f^{\prime \prime}\),\(K_f^{\prime}\) або, щоб визначити склад системи при рівновазі.
Зауважте, що після точки еквівалентності титранд є буфером комплексоутворення метал-ліганд, причому PcD визначається C EDTA та [cDy 2—]. Буфер знаходиться на нижній межі,\(\text{pCd} = \log{K_f^{\prime}} - 1\) коли
\[\frac{C_{\mathrm{EDTA}}}{\left[\mathrm{CdY}^{2-}\right]} = \frac {(\text{mole EDTA})_\text{added} - (\text{mol Cd}^{2+})_\text{initial}} {(\text{mol Cd}^{2+})_\text{initial}} = \frac {1} {10} \nonumber\]
Здійснюючи відповідні заміни та вирішуючи, ми виявляємо, що
\[\frac{M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}=\frac{1}{10} \nonumber\]
\[M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}=0.1 \times M_{\mathrm{Cd}} V_{\mathrm{Cd}} \nonumber\]
\[V_{\mathrm{EDTA}}=\frac{1.1 \times M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=1.1 \times V_{e q} \nonumber\]
Таким чином, коли титрування досягає 110% об'єму точки еквівалентності, pCd є\(\log{K_f^{\prime}} - 1\). Подібний розрахунок повинен переконати вас, що PcD - це\(\log{K_f^{\prime}} + 1\) коли обсяг ЕДТА є\(2 \times V_\text{eq}\).
Рисунок Template:index c показує третій крок нашого ескізу. Спочатку ми додаємо діаграму сходів для комплексу CDY 2—, включаючи його буферний діапазон, використовуючи його\(\log{K_f^{\prime}}\) значення 16.04. Далі ми додаємо дві точки, одну для PcD при 110% V екв (pCd 15,04 при 27,5 мл) і одну для PcD при 200% V екв (pCd 16,04 при 50,0 мл).
Далі проводимо пряму лінію через кожну пару точок, протягуючи кожну лінію через вертикальну лінію, яка вказує на об'єм точки еквівалентності (Рисунок Template:index d). Нарешті, ми завершуємо наш ескіз, намалювавши плавну криву, яка з'єднує три прямолінійні відрізки (Рисунок Template:index e). Порівняння нашого ескізу з точною кривою титрування (рис. Template:index f) показує, що вони знаходяться в тісній згоді.
Наше лікування тут загальне і застосовується до будь-якого комплексоутворення титрування з використанням ЕДТА як титранту.
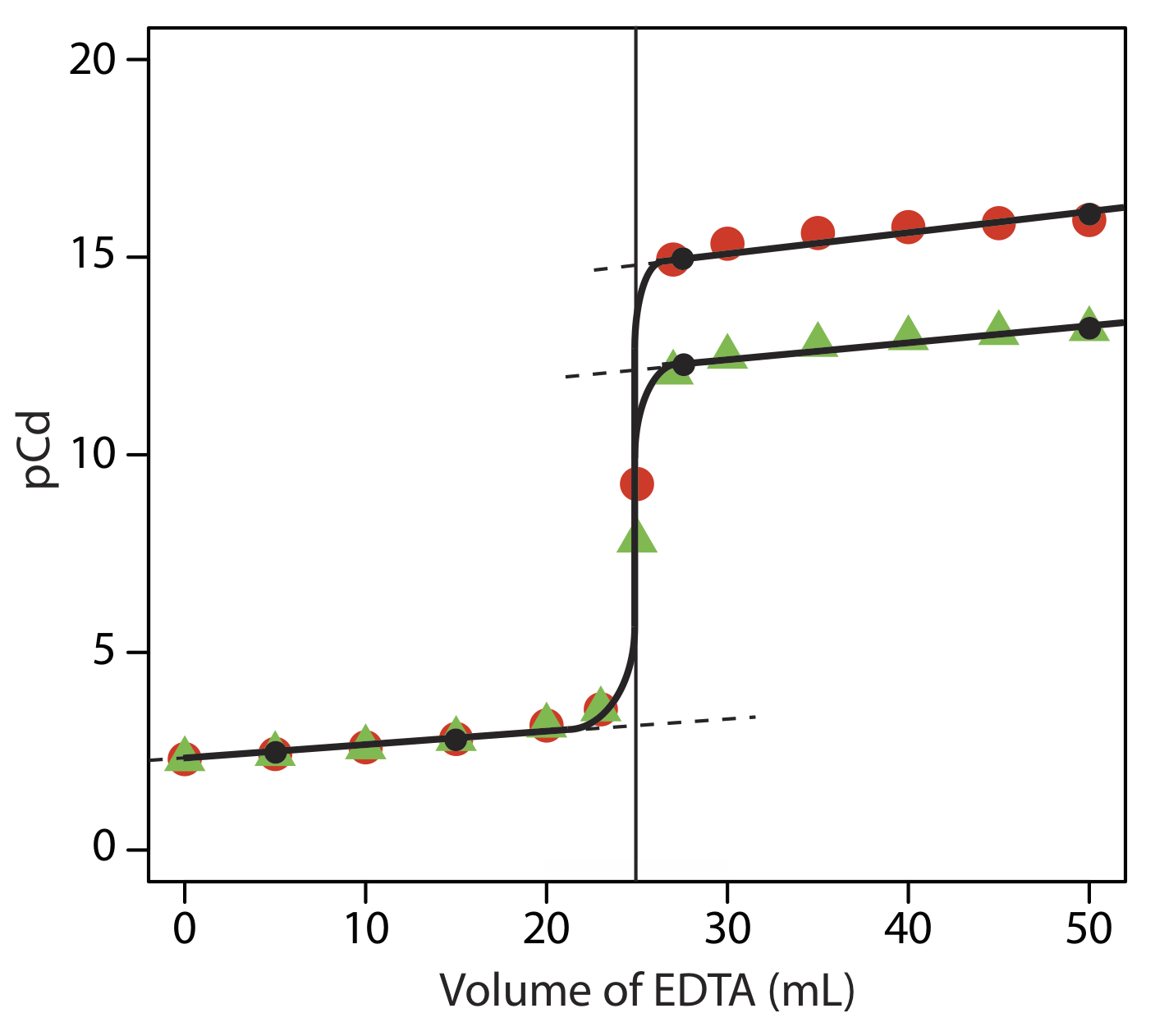
Ескізні криві титрування для титрування 50,0 мл\(5.00 \times 10^{-3}\) M Cd 2 + з 0,0100 М ЕДТА (а) при рН 10 і (b) при рН 7. Порівняйте ваші ескізи з обчисленими кривими титрування з вправи Template:index.
- Відповідь
-
На малюнку нижче показаний ескіз кривих титрування. Дві чорні точки перед точкою еквівалентності (V EDTA = 5 мл, PCD= 2.43 і V EDTA = 15 мл, PCD= 2.81) однакові для обох PHS і взяті з результатів вправи Template:index. Дві чорні точки після точки еквівалентності для рН 7 (V EDTA = 27,5 мл, PCD= 12,2 і V EDTA = 50 мл, PCD= 13.2) наносяться\(\log{K_f^{\prime}}\) з використанням 13.2 для CdY 2 -. Дві точки після точки еквівалентності для рН 10 (V ЕДТА = 27,5 мл, PCD= 15,0 і V EDTA = 50 мл, PCD= 16,0) побудовані\(\log{K_f^{\prime}}\) з використанням 16,0 для CdY 2 -. Точки червоного кольору - це обчислення з вправи Template:index для рН 10, а точки зеленим кольором - це обчислення з вправи Template:index для рН 7.
Вибір та оцінка кінцевої точки
Точка еквівалентності титрування комплексоутворення виникає, коли ми реагуємо стехіометрично еквівалентні кількості титранду та титранту. Як і у випадку кислотно-лужного титрування, ми оцінюємо точку еквівалентності титрування комплексоутворення з використанням експериментальної кінцевої точки. Для визначення місцезнаходження кінцевої точки доступні різні методи, включаючи індикатори і датчики, які реагують на зміну умов рішення.
Пошук кінцевої точки за допомогою індикатора
Більшість показників титрування комплексоутворення - це органічні барвники, відомі як металохромні показники - які утворюють стабільні комплекси з іонами металів. Показник, In m —, додається до розчину титранду, де він утворює стійкий комплекс з іоном металу, mIn n —. Коли ми додаємо ЕДТА, він реагує спочатку з вільними іонами металів, а потім витісняє показник з mIn n —.
\[\text{MIn}^{n-}(aq) + \text{Y}^{4-}(aq) \rightarrow \text{MY}^{2-}(aq) + \text{In}^{m-}(aq) \nonumber\]
Якщо mIn n — і In m — мають різні кольори, то зміна кольору сигналізує про кінцеву точку.
Точність кінцевої точки індикатора залежить від міцності комплексу метал—індикатор відносно міцності комплексу метал—ЕДТА. Якщо комплекс метал-індикатор занадто сильний, зміна кольору відбувається після точки еквівалентності. Однак, якщо комплекс метал-індикатор занадто слабкий, кінцева точка виникає до того, як ми досягнемо точки еквівалентності.
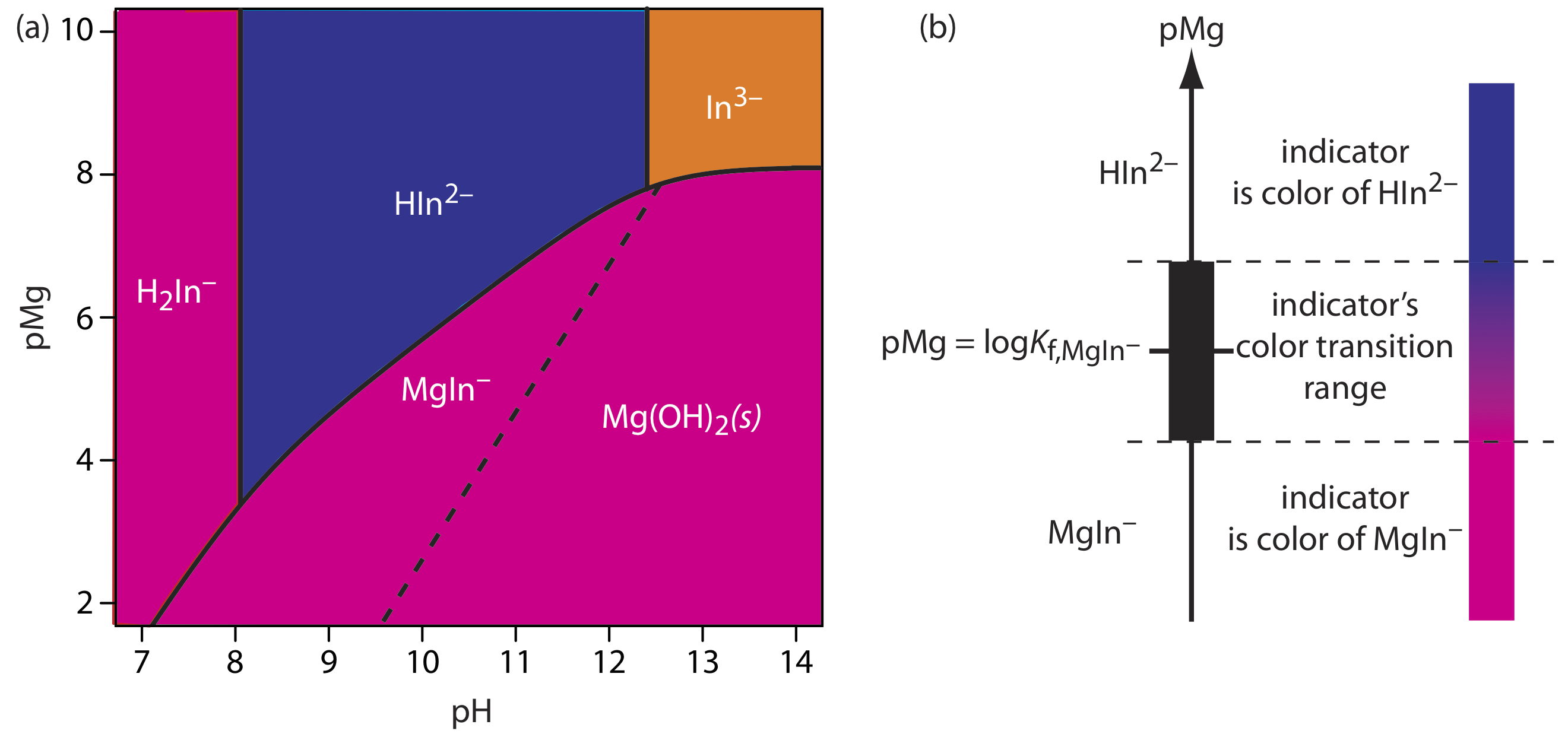
Більшість металохромних показників також є слабкими кислотами. Одним з наслідків цього є те, що умовна константа формування комплексу метал—індикатор залежить від рН титранду. Це забезпечує певний контроль над похибкою титрування індикатора, оскільки ми можемо регулювати міцність комплексу метал-індикатор, регулюючи рН, при якому ми проводимо титрування. На жаль, оскільки показник є слабкою кислотою, колір некомплексного індикатора також може змінюватися з рН. На малюнку Template:index, наприклад, показаний колір калмагіту індикатора як функції рН і PMg, де H 2 In —, HiN 2— і In 3— є різними формами некомплексного індикатора, а MgIn — Mg 2 + —кальмагітовий комплекс. Оскільки колір комплексу метал-індикатор кальмагіту червоний, його використання в якості металохромного індикатора має практичний діапазон рН приблизно 8,5-11, де некомплексний показник, HiN 2—, має синій колір.
У таблиці Template:index наведено приклади металохромних показників та умов іонів металів та рН, для яких вони корисні. Навіть якщо відповідного показника не існує, часто можна завершити титрування ЕДТА шляхом введення невеликої кількості вторинного комплексу метал-ЕДТА, якщо вторинний іон металу утворює більш міцний комплекс з індикатором і слабший комплекс з ЕДТА, ніж аналіт. Наприклад, кальмагіт має погану кінцеву точку при титруванні Ca 2 + за допомогою ЕДТА. Додавання невеликої кількості Mg 2 + —EDTA до титранду дає більш різку кінцеву точку. Оскільки Ca 2+ утворює сильніший комплекс з ЕДТА, він витісняє Mg 2 +, який потім утворює червоний колір Mg 2 + -кальмагітовий комплекс. У кінцевій точці титрування ЕДТА витісняє Mg 2 + з комплексу Mg 2 + —кальмагіт, сигналізуючи про кінцеву точку наявністю синьої форми некомплексного індикатора.
| показник | діапазон рН | іони металів | показник | діапазон рН | іони металів |
|---|---|---|---|---|---|
| кальмагіт | 8.5—11 | Ба, Са, Мг, Zn | Еріохром Чорний T | 7,5—10,5 | Ба, Са, Мг, Zn |
| Еріохром Синій Чорний R | 8—12 | Са, Мг, Zn, Cu | КАСТРУЛЯ | 2—11 | Cd, Cu, Zn |
| мурексид | 6—13 | Са, Ni, Cu | саліцилова кислота | 2—3 | Fe |
|
всі іони металів несуть заряд +2 чекають на залізо, який становить +3 іони металів курсивом мають погані кінцеві точки |
|||||
Пошук кінцевої точки шляхом моніторингу поглинання
Важливим обмеженням при використанні металохромного індикатора є те, що ми повинні мати можливість бачити зміну кольору індикатора в кінцевій точці. Це може бути важко, якщо розчин вже пофарбований. Наприклад, при титруванні Cu 2 + з ЕДТА використовується аміак для регулювання рН титранду. Інтенсивно\(\text{Cu(NH}_3)_2^{4+}\) забарвлений комплекс затьмарює колір індикатора, що ускладнює точне визначення кінцевої точки. Інші поглинаючі види, присутні в матриці зразка, також можуть перешкоджати. Це часто є проблемою при аналізі клінічних зразків, таких як кров, або екологічних зразків, таких як природні води.
Якщо принаймні один вид в комплексоутворення титрування поглинає електромагнітне випромінювання, то ми можемо визначити кінцеву точку, контролюючи поглинання титранду на ретельно підібраній довжині хвилі. Наприклад, ми можемо визначити кінцеву точку титрування Cu 2 + з ЕДТА в присутності NH 3 шляхом моніторингу поглинання титранду на довжині хвилі 745 нм, де\(\text{Cu(NH}_3)_2^{4+}\) комплекс сильно поглинає. На початку титрування поглинання знаходиться на максимумі. Як ми додаємо ЕДТА, однак, реакція
\[\text{Cu(NH}_3)_4^{2+}(aq) + \text{Y}^{4-} \rightleftharpoons \text{CuY}^{2-}(aq) + 4\text{NH}_3(aq) \nonumber\]
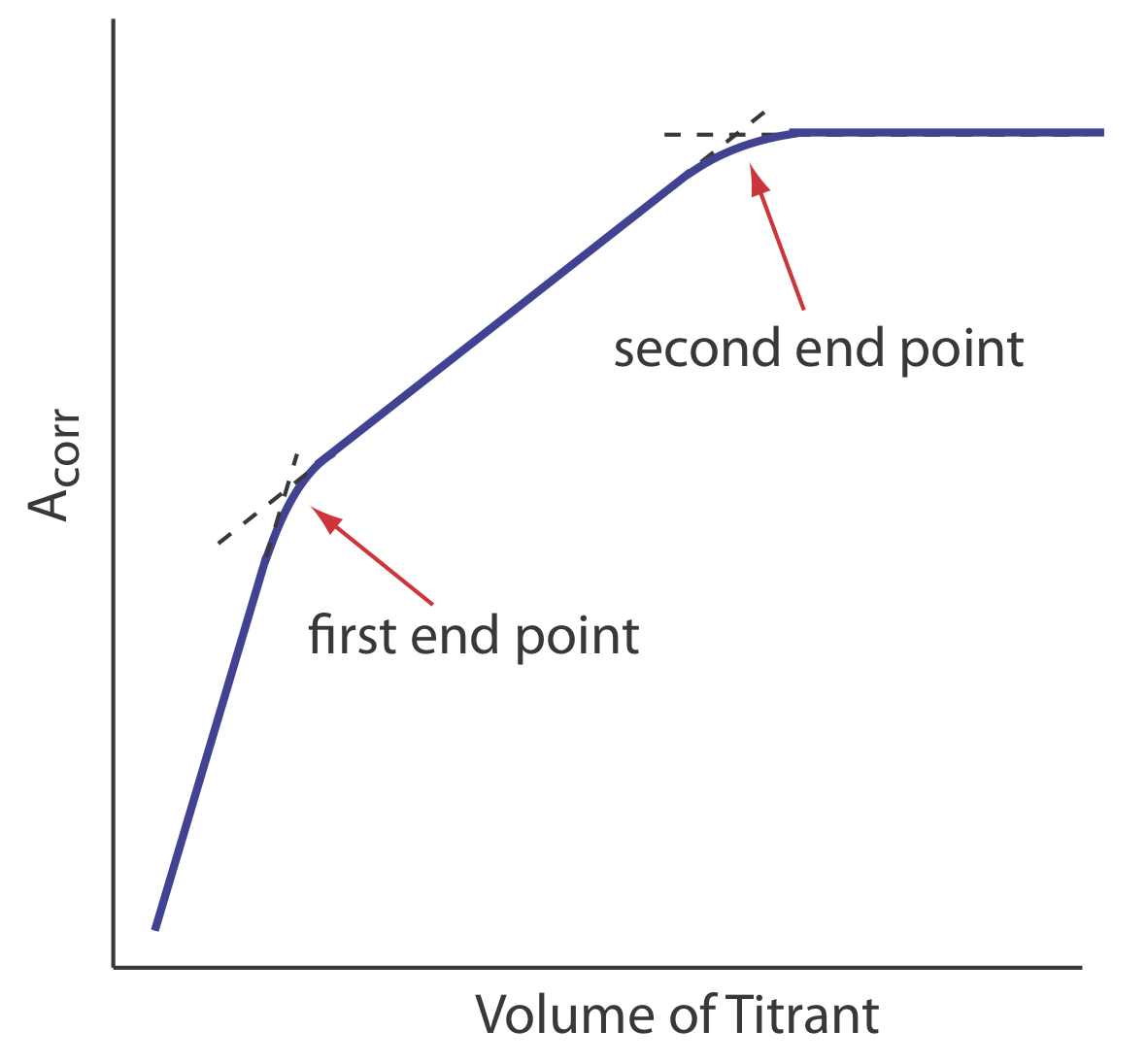
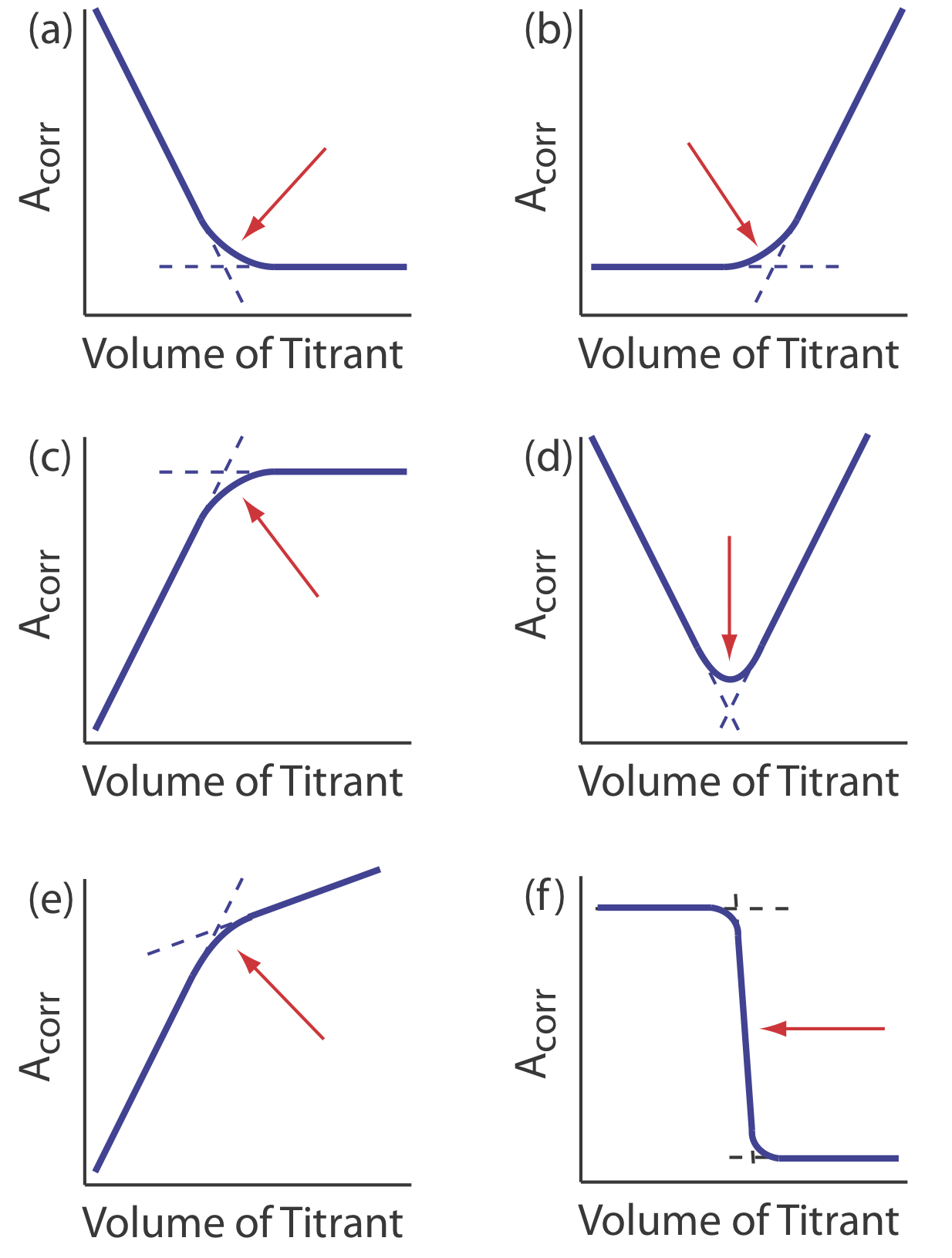
зменшує концентрацію\(\text{Cu(NH}_3)_2^{4+}\) і зменшує поглинання, поки ми не досягнемо точки еквівалентності. Після точки еквівалентності поглинання по суті залишається незмінним. Отримана спектрофотометрична крива титрування показана на рисунку Template:index a. Зауважте, що вісь y кривої титрування є не вимірюваним поглинанням, A meas, а виправленим поглинанням, A corr
\[A_\text{corr} = A_\text{meas} \times \frac {V_\text{EDTA} + V_\text{Cu}} {V_\text{Cu}} \nonumber\]
де V ЕДТА і V Cu - це, відповідно, обсяги ЕДТА і Cu. Виправлення поглинання для розведення титранду гарантує, що спектрофотометрична крива титрування складається з лінійних сегментів, які ми можемо екстраполювати, щоб знайти кінцеву точку. Інші поширені спектрофотометричні криві титрування показані на малюнках Template:index b-f.
Представницький метод 9.3.1: Визначення жорсткості води та стічних вод
Найкращий спосіб оцінити теоретичні та практичні деталі, розглянуті в цьому розділі, - це уважно вивчити типовий титриметричний метод комплексоутворення. Хоча кожен метод унікальний, наступний опис визначення жорсткості води дає повчальний приклад типової процедури. Опис тут базується на методі 2340C, опублікованому в Стандартні методи дослідження води та стічних вод, 20-е видання, Американська асоціація громадського здоров'я: Вашингтон, округ Колумбія, 1998.
Опис методу
Оперативне визначення жорсткості води - це сумарна концентрація катіонів в зразку, які можуть утворювати нерозчинний комплекс з милом. Хоча більшість двовалентних і тривалентних іонів металів сприяють твердості, двома найважливішими іонами металів є Ca 2 + і Mg 2 +. Твердість визначається титруванням ЕДТА при буферному рН 10. В якості індикатора використовується кальмагіт. Твердість повідомляється як мг СаСО 3 /л.
Порядок дій
Виберіть обсяг зразка, який вимагає менше 15 мл титранту, щоб зберегти час аналізу менше 5 хвилин і, якщо необхідно, розбавити зразок до 50 мл дистильованою водою. Відрегулюйте рН зразка, додавши 1—2 мл буфера pH 10, який містить невелику кількість Mg 2 + —EDTA. Додайте 1—2 краплі індикатора і титруйте стандартним розчином ЕДТА, поки кінцева точка червоно-синього не буде досягнута (Рисунок Template:index).

Питання
1. Чому зразок буферизований до рН 10? Які проблеми ви можете очікувати при більш високому pH або нижчому pH?
З двох первинних катіонів, які сприяють твердості, Mg 2 + утворює слабший комплекс з ЕДТА і є останнім катіоном, який реагує з титрантом. Calmagite є корисним індикатором, оскільки він дає чітку кінцеву точку при титруванні Mg 2 + (див. Таблицю Template:index). Через кислотно-базові властивості кальмагіту діапазон значень pMg, протягом яких індикатор змінює колір, залежить від рН титранду (Рисунок Template:index). Рисунок Template:index показує криву титрування для 50-мл розчину 10 —3 M Mg 2 + з 10 —2 М ЕДТА при рН 9, 10 та 11. На кожну криву титрування накладається діапазон умов, за якими середньостатистичний аналітик буде спостерігати кінцеву точку. При рН 9 можлива рання кінцева точка, що призводить до негативної детермінантної похибки. Пізня кінцева точка і позитивна детермінантна похибка можливі, якщо рН дорівнює 11.
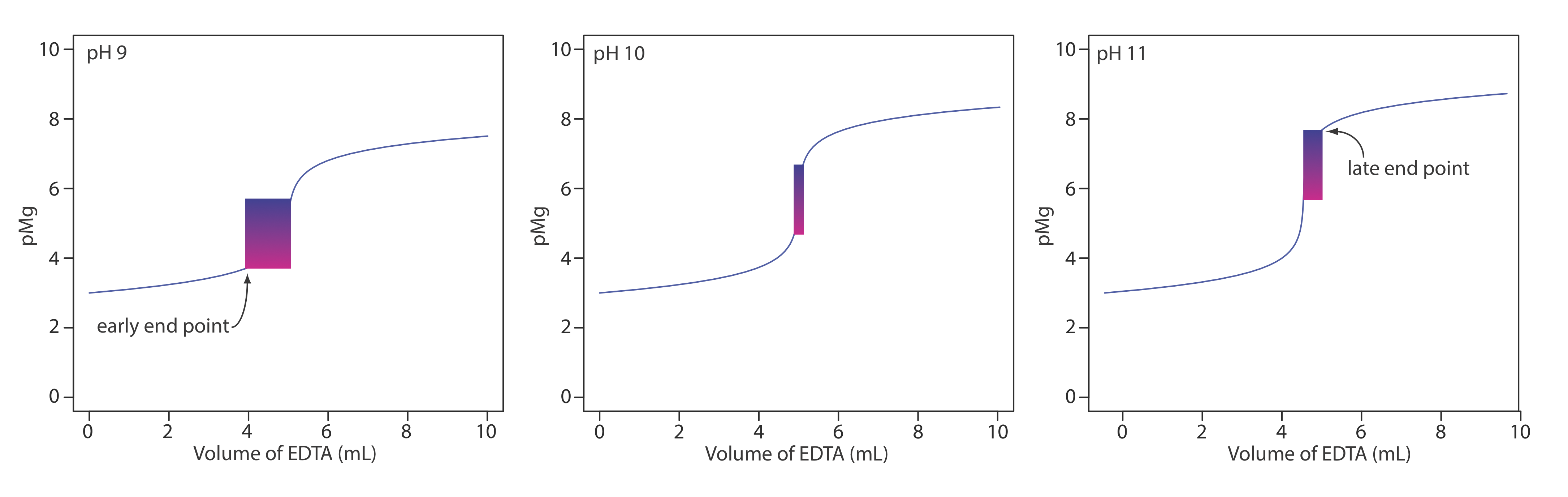
2. Чому в буфер додається невелика кількість комплексу Mg 2 + —EDTA?
Кінцева точка титрування сигналізується індикатором кальмагіт. Кінцева точка індикатора з Mg 2 + відрізняється, але його зміна кольору при титруванні Ca 2 + не забезпечує хорошої кінцевої точки (див. Таблицю Template:index). Якщо зразок не містить жодного Mg 2 + в якості джерела твердості, то кінцева точка титрування визначена погано, що призводить до неточного і неточного результату. Додавання невеликої кількості Mg 2 + —EDTA до буфера гарантує, що титранд включає принаймні деякі Mg 2 +. Оскільки Са 2 + утворює більш сильний комплекс з ЕДТА, він витісняє Mg 2 + з комплексу Mg 2 + —EDTA, звільняючи Mg 2 + зв'язуватися з індикатором. Це зміщення є стехіометричним, тому загальна концентрація катіонів твердості залишається незмінною. Зсув ЕДТА Mg 2+ від Mg 2 + —індикаторного комплексу сигналізує про кінцеву точку титрування.
3. Чому в процедурі вказується, що титрування займає не більше 5 хвилин?
Обмеження за часом свідчить про наявність кінетично керованої перешкоди, можливо, що виникає внаслідок конкуруючої хімічної реакції. В даному випадку перешкодою є можливе осадження СаСО 3 при рН 10.
Кількісні програми
Хоча багато кількісних застосувань комплексоутворення титриметрії були замінені іншими аналітичними методами, кілька важливих застосувань продовжують знаходити актуальність. У розділі ми розглядаємо загальне застосування комплексоутворення титриметрії з акцентом на додатки з аналізу води та стічних вод. Однак спочатку ми обговорюємо вибір та стандартизацію титрантів комплексоутворення.
Вибір і стандартизація титрантів
ЕДТА - це універсальний титрант, який може бути використаний для аналізу практично всіх іонів металів. Хоча ЕДТА є звичайним титрантом, коли титранд є іоном металу, його не можна використовувати для титрування аніонів, для яких Ag + або Hg 2 + підходять титранти.
Розчини ЕДТА готують з його розчинної динатрієвої солі, Na 2 H 2 Y•2H 2 O, і стандартизують шляхом титрування проти розчину, виготовленого з первинного стандарту CaCo 3. Розчини Ag + і Hg 2 + готують з використанням AgNO 3 і Hg (NO 3) 2, обидва з яких є вторинними стандартами. Стандартизація здійснюється шляхом титрування проти розчину, приготованого з первинного стандартного сорту NaCl.
неорганічні аналіти
Титріметрія комплексоутворення продовжує перераховуватися як стандартний метод визначення твердості, Ca 2+, CN — і Cl — у водах і стічних водах. Оцінка твердості була описана раніше в репрезентативному методі 9.3.1. Визначення Са 2 + ускладнюється наявністю Mg 2 +, який також реагує з ЕДТА. Для запобігання перешкод рН регулюється до 12—13, який осаджує Mg 2 + як Mg (OH) 2. Титрування за допомогою ЕДТА з використанням мурексиду або Еріохрому Blue Black R в якості індикатора дає концентрацію Са 2 +.
Ціанід визначають при концентраціях більше 1 мг/л шляхом внесення зразка лужним з NaOH і титрування стандартним розчином AgNO 3 з утворенням розчинного\(\text{Ag(CN)}_2^-\) комплексу. Кінцева точка визначається за допомогою р -диметиламінобензалродаміну як індикатора, при цьому розчин переходить з жовтого кольору в лососевий колір при наявності надлишку Ag +.
Хлорид визначають титруванням Hg (NO 3) 2, утворюючи HgCl 2 (aq). Пробу підкислюють до рН 2,3-3,8 і індикатором служить дифенилкарбазон, який утворює кольоровий комплекс з надлишком Hg 2 +. Індикатор рН ксилол ціанол FF додається, щоб гарантувати, що рН знаходиться в потрібному діапазоні. Вихідним розчином є зеленувато-блакитний колір, а титрування проводиться до фіолетової кінцевої точки.
Кількісні розрахунки
Кількісний зв'язок між титрандом і титрантом визначається стехіометрією реакції титрування. Для титрування за допомогою ЕДТА стехіометрія завжди дорівнює 1:1.
Концентрацію розчину ЕДТА визначають шляхом стандартизації проти розчину Са 2 +, приготованого з використанням первинного стандарту CaCo 3. 0,4071 г зразка CaCo 3 переносять в об'ємну колбу об'ємом 500 мл, розчиняють з використанням мінімум 6 М HCl, і розводять до об'єму. Після перенесення 50.00-мл порції цього розчину в 250-мл колбу Ерленмейера, рН регулюють шляхом додавання 5 мл pH 10 NH 3 -NH 4 Cl буфера, який містить невелику кількість Mg 2 + —EDTA. Після додавання кальмагіту в якості індикатора розчин титрують ЕДТА, для досягнення кінцевої точки потрібно 42,63 мл. Повідомте про молярну концентрацію ЕДТА в титранті.
Рішення
Первинний стандарт Са 2+ має концентрацію
\[\frac {0.4071 \text{ g CaCO}_3}{0.5000 \text{ L}} \times \frac {1 \text{ mol Ca}^{2+}}{100.09 \text{ g CaCO}_3} = 8.135 \times 10^{-3} \text{ M Ca}^{2+} \nonumber\]
Родимки Са 2+ в титранді
\[8.135 \times 10^{-3} \text{ M Ca}^{2+} \times 0.05000 \text{ L} = 4.068 \times 10^{-4} \text{ mol Ca}^{2+} \nonumber\]
що означає, що в титруванні використовуються\(4.068 \times 10^{-4}\) родимки ЕДТА. Молярність ЕДТА в титранті становить
\[\frac {4.068 \times 10^{-4} \text{ mol Ca}^{2+}}{0.04263 \text{ L}} = 9.543 \times 10^{-3} \text{ M EDTA} \nonumber\]
Зразок 100.0-мл аналізують на твердість за допомогою процедури, викладеної в репрезентативному методі 9.3.1, що вимагає 23.63 мл 0,0109 М ЕДТА. Повідомити про твердість зразка як мг CaCo 3 /L.
- Відповідь
-
При аналізі на твердість ми ставимося до зразка так, ніби Са 2 + є єдиним іоном металу, який реагує з ЕДТА. Отже, грами Са 2 + у зразку
\[(0.0109 \text{ M EDTA})(0.02363 \text{ L}) \times \frac {1 \text{ mol Ca}^{2+}}{\text{mol EDTA}} = 2.58 \times 10^{-4} \text{ mol Ca}^{2+} \nonumber\]
\[2.58 \times 10^{-4} \text{ mol Ca}^{2+} \times \frac {1 \text{ mol CaCO}_3}{\text{mol Ca}^{2+}} \times \frac {100.09 \text{ g CaCO}_3}{\text{mol CaCO}_3} = 0.0258 \text{ g CaCO}_3 \nonumber\]
і твердість зразка
\[\frac {0.0258 \text{ g CaCO}_3}{0.1000 \text{ L}} \times \frac {1000 \text{ mg}}{\text{g}} = 258 \text{ g CaCO}_3\text{/L} \nonumber\]
Як показано в наступному прикладі, ми можемо розширити цей розрахунок до реакцій комплексоутворення, які використовують інші титранти.
Концентрація Cl — у зразку води з прісноводного водоносного шару 100.0-мл перевіряється на зазіхання морської води титруванням 0,0516 M Hg (NO 3) 2. Зразок підкислюють і титрують до кінцевої точки дифенілкарбазону, що вимагає 6,18 мл титранту. Повідомити про концентрацію Cl —, в мг/л, в водоносному шарі.
Рішення
Реакція між Cl - і Hg 2 + виробляє комплекс метал-ліганд HgCl 2 (aq). Кожен моль Hg 2 + реагує з 2 молями Cl —; таким чином
\[\frac {0.0516 \text{ mol Hg(NO}_3)_2}{\text{L}} \times 0.00618 \text{ L} \times \frac {2 \text{ mol Cl}^-}{\text{mol Hg(NO}_3)_2} \times \frac {35.453 \text{ g Cl}^-}{\text{mol Cl}^-} = 0.0226 \text{ g Cl}^- \nonumber\]
знаходяться в зразку. Концентрація Cl — у зразку становить
\[\frac {0.0226 \text{ g Cl}^-}{0.1000 \text{ L}} \times \frac {1000 \text{ mg}}{\text{g}} = 226 \text{ mg/L} \nonumber\]
0.4482-г зразок нечистого NaCN титрують 0,1018 М AgNO 3, що вимагає 39,68 мл для досягнення кінцевої точки. Повідомити про чистоту зразка як %w/w NaCN.
- Відповідь
-
Титрування CN — з Ag + виробляє комплекс метал-лігандів\(\text{Ag(CN)}_2^-\); таким чином, кожен моль AgNO 3 реагує з двома молями NaCN. Грами NaCN у зразку
\[(0.1018 \text{ M AgNO}_3)(0.03968 \text{ L}) \times \frac {2 \text{ mol NaCN}}{\text{mol AgNO}_3} \times \frac {49.01 \text{ g NaCN}}{\text{mol NaCN}} = 0.3959 \text{ g NaCN} \nonumber\]
і чистота зразка
\[\frac {0.3959 \text{ g NaCN}}{0.4482 \text{ g sample}} \times 100 = 88.33 \text{% w/w NaCN} \nonumber\]
Нарешті, можливі складні титрування за участю декількох аналітів або зворотного титрування.
Сплав хромелю, що містить Ni, Fe та Cr, аналізується шляхом комплексоутворення титрування з використанням ЕДТА як титранту. 0,7176-г зразок сплаву розчиняють в HNO 3 і розводять до 250 мл в об'ємній колбі. 50,00-мл аліквота зразка, обробленого пірофосфатом для маскування Fe та Cr, вимагає 26,14 мл 0,05831 М ЕДТА, щоб досягти кінцевої точки мурексиду. Другу 50,00-мл аліквоти обробляють гексаметилентетраміном для маскування Cr. Титрування з 0.05831 M EDTA вимагає 35,43 мл, щоб досягти кінцевої точки мурексиду. Нарешті, третій 50,00-мл аліквота обробляють 50,00 мл 0,05831 М ЕДТА, а назад титрують до кінцевої точки мурексиду 6,21 мл 0,06316 M Cu 2 +. Повідомте про вагові відсотки Ni, Fe та Cr у сплаві.
Рішення
Стехіометрія між ЕДТА та кожним іоном металу становить 1:1. Отже, для кожного з трьох титрувань ми можемо написати рівняння, яке пов'язує молі ЕДТА з молями іонів металів, які титруються.
титрування 1: моль Ni = моль ЕДТА
титрування 2: моль Ni+моль Fe = моль ЕДТА
титрування 3: моль Ni+моль Fe + моль Cr+моль Cu = моль ЕДТА
Ми використовуємо перше титрування, щоб визначити молі Ni в нашій 50,00-мл порції розчиненого сплаву. Титрування використовує
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.02614 \text{ L} = 1.524 \times 10^{-3} \text{ mol EDTA} \nonumber\]
що означає, що зразок містить\(1.524 \times 10^{-3}\) моль Ni.
Визначивши молі ЕДТА, які реагують з Ni, використовуємо друге титрування для визначення кількості Fe в зразку. Друге титрування використовує
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.03543 \text{ L} = 2.066 \times 10^{-3} \text{ mol EDTA} \nonumber\]
з яких\(1.524 \times 10^{-3}\) моль використовується для титрування Ni. Це залишає\(5.42 \times 10^{-4}\) моль ЕДТА реагувати з Fe; таким чином, зразок містить\(5.42 \times 10^{-4}\) моль Fe.
Нарешті, ми можемо використовувати третє титрування для визначення кількості Cr в сплаві. Третє титрування використовує
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.0500 \text{ L} = 3.926 \times 10^{-3} \text{ mol EDTA} \nonumber\]
з яких\(1.524 \times 10^{-3}\) моль використовується для титрування Ni і\(5.42 \times 10^{-4}\) моль використовуються для титрування Fe. Це залишає\(8.50 \times 10^{-4}\) моль ЕДТА реагувати з Cu та Cr. Кількість ЕДТА, що реагує з Cu, становить
\[\frac {0.06316 \text{ mol Cu}^{2+}}{\text{L}} \times 0.006211 \text{ L} \times \frac {1 \text{ mol EDTA}}{\text{mol Cu}^{2+}} = 3.92 \times 10^{-4} \text{ mol EDTA} \nonumber\]
залишаючи\(4.58 \times 10^{-4}\) моль ЕДТА реагувати з Cr. Таким чином, зразок містить\(4.58 \times 10^{-4}\) моль Cr.
Визначивши молі Ni, Fe та Cr в 50,00-мл частини розчиненого сплаву, ми можемо обчислити %w/w кожного аналіту в сплаві.
\[\frac {1.524 \times 10^{-3} \text{ mol Ni}}{50.00 \text{ mL}} \times \frac {58.69 \text{ g Ni}}{\text{mol Ni}} = 0.4472 \text{ g Ni} \nonumber\]
\[\frac {0.4472 \text{ g Ni}}{0.7176 \text{ g sample}} \times 100 = 62.32 \text{% w/w Ni} \nonumber\]
\[\frac {5.42 \times 10^{-4} \text{ mol Fe}}{50.00 \text{ mL}} \times \frac {55.845 \text{ g Fe}}{\text{mol Fe}} = 0.151 \text{ g Fe} \nonumber\]
\[\frac {0.151 \text{ g Fe}}{0.7176 \text{ g sample}} \times 100 = 21.0 \text{% w/w Fe} \nonumber\]
\[\frac {4.58 \times 10^{-4} \text{ mol Cr}}{50.00 \text{ mL}} \times \frac {51.996 \text{ g Cr}}{\text{mol Cr}} = 0.119 \text{ g Cr} \nonumber\]
\[\frac {0.119 \text{ g Cr}}{0.7176 \text{ g sample}} \times 100 = 16.6 \text{% w/w Cr} \nonumber\]
Непряме комплексоутворення титрування з ЕДТА може бути використано для визначення концентрації сульфату\(\text{SO}_4^{2-}\), в пробі. Зразок 0,157-г розчиняють у воді, і будь-який присутній сульфат осаджується як BaSO 4 шляхом додавання Ba (NO 3) 2. Після проціджування і промивання осаду його розчиняють в 25,00 мл 0,02011 М ЕДТА. Надлишок ЕДТА титрується 0.01113 M Mg 2 +, що вимагає 4.23 мл для досягнення кінцевої точки. Обчисліть %w/w Na 2 SO 4 у зразку.
- Відповідь
-
Загальні родимки ЕДТА, що використовуються в цьому аналізі
\[(0.02011 \text{ M EDTA})(0.02500 \text{ L}) = 5.028 \times 10^{-4} \text{ mol EDTA} \nonumber\]
З цього
\[(0.01113 \text{ M Mg}^{2+})(0.00423 \text{ L}) \times \frac {1 \text{ mol EDTA}}{\text{mol Mg}^{2+}} = 4.708 \times 10^{-5} \text{ mol EDTA} \nonumber\]
споживаються при зворотному титруванні з Mg 2 +, що означає, що
\[5.028 \times 10^{-4} \text{ mol EDTA} - 4.708 \times 10^{-5} \text{ mol EDTA} = 4.557 \times 10^{-4} \text{ mol EDTA} \nonumber\]
реагувати з BasO 4. Кожен моль BaSO 4 реагує з одним молем ЕДТА; таким чином
\[4.557 \times 10^{-4} \text{ mol EDTA} \times \frac {1 \text{ mol BaSO}_4}{\text{mol EDTA}} \times \frac {1 \text{ mol Na}_2\text{SO}_4}{\text{mol BaSO}_4} \times \frac {142.04 \text{ g Na}_2\text{SO}_4}{\text{mol Na}_2\text{SO}_4} = 0.06473 \text{ g Na}_2\text{SO}_4 \nonumber\]
\[\frac{0.06473 \text{ g Na}_2\text{SO}_4}{0.1557 \text{ g sample}} \times 100 = 41.57 \text{% w/w Na}_2\text{SO}_4 \nonumber\]
Оцінка комплексоутворення титриметрії
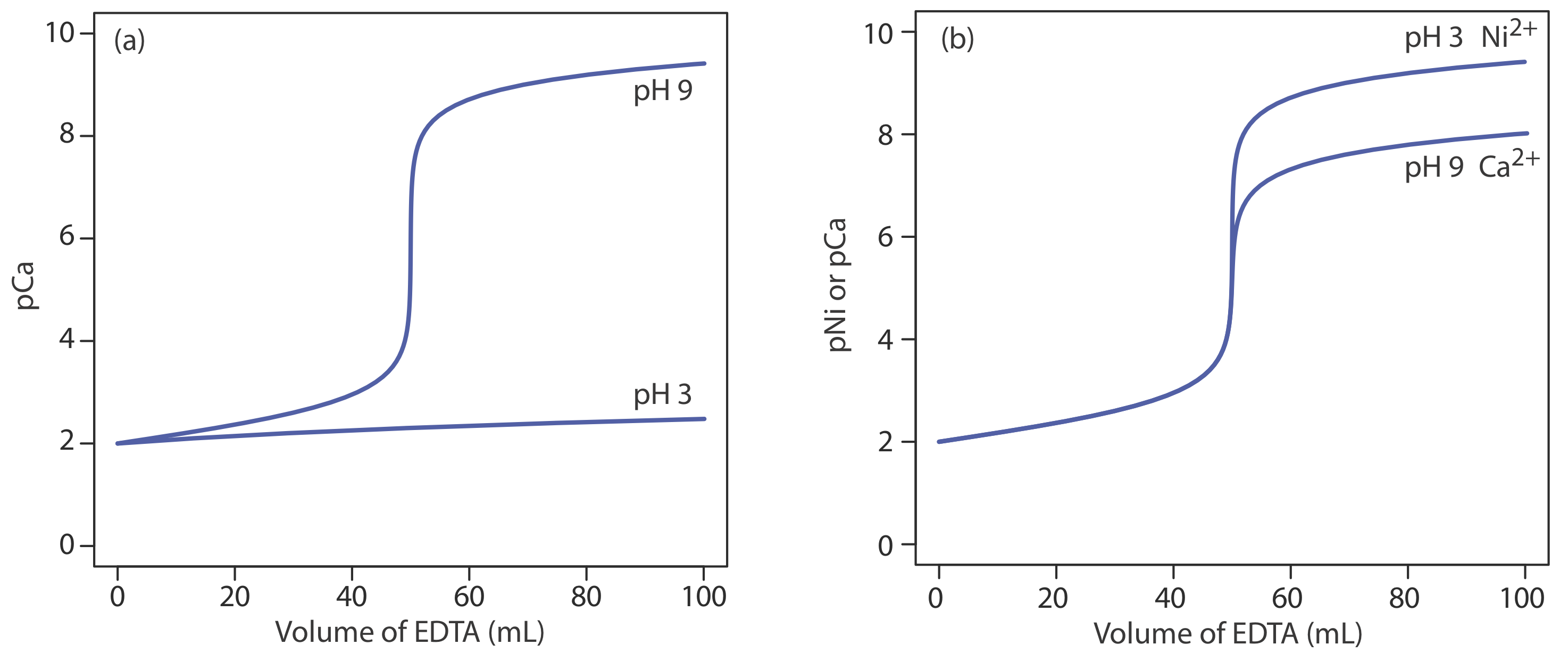
Масштаб операцій, точність, точність, чутливість, час та вартість комплексоутворення подібні до описаних раніше для кислотно-лужних титрувань. Титрування комплексоутворення, однак, є більш вибірковими. Хоча ЕДТА утворює сильні комплекси з більшістю іонів металів, ретельно контролюючи рН титранду, ми можемо аналізувати зразки, які містять два або більше аналітів. Причина, по якій ми можемо використовувати рН для забезпечення селективності, показана на малюнку Template:index a. Титрування Ca 2+ при рН 9 має чіткий розрив кривої титрування, оскільки умовна константа формування для CaY 2— of\(2.6 \times 10^9\) досить велика, щоб гарантувати, що реакція Са 2 + і ЕДТА йде до завершення. При рН 3, однак, умовна константа утворення 1,23 настільки мала, що дуже мало Ca 2 + реагує з ЕДТА. Припустимо, нам потрібно проаналізувати суміш Ni 2 + і Ca 2 +. Обидва аналіти реагують з ЕДТА, але їх умовні константи формування значно відрізняються. Якщо ми відрегулюємо рН до 3, ми можемо титрувати Ni 2 + за допомогою ЕДТА без титрування Ca 2 + (Рисунок {{Template.index (ID:9)} b). Коли титрування завершено, ми регулюємо рН титранду до 9 і титруємо Ca 2 + за допомогою ЕДТА.
Спектрофотометричне титрування є особливо корисним підходом для аналізу суміші аналітів. Наприклад, як показано на рисунку Template:index, ми можемо визначити концентрацію двох іонів металу, якщо існує різниця між поглинанням двох комплексів метал-лігандів.