6.7: Розв'язування задач рівноваги

Сходові діаграми є корисним інструментом для оцінки хімічної реакційної здатності та для забезпечення обґрунтованої оцінки складу хімічної системи при рівновазі. Якщо нам потрібен більш точний кількісний опис умови рівноваги, то діаграма сходів недостатня; натомість нам потрібно знайти алгебраїчне рішення. У цьому розділі ми дізнаємося, як налаштовувати та вирішувати проблеми рівноваги. Почнемо з простої проблеми і працюємо над більш складними завданнями.

Проста задача: Розчинність Pb (IO ₃) ₂

Якщо ми помістимо нерозчинну сполуку, таку як Pb (IO ₃) ₂ в деіонізовану воду, тверда речовина розчиняється до концентрації Pb ^{2 +} і\(\text{IO}_3^-\) задовольнить продукт розчинності для Pb (IO ₃) ₂. При рівновазі розчин насичується Pb (IO ₃) ₂, що означає просто, що більше не може розчинитися жодне тверде тіло. Як ми визначаємо рівноважні концентрації Pb ^{2 +} і\(\text{IO}_3^-\), і яка молярна розчинність Pb (IO ₃) ₂ в цьому насиченому розчині?

Коли ми вперше додаємо твердий Pb (IO ₃) ₂ до води, концентрації Pb ^{2 +} і\(\text{IO}_3^-\) дорівнюють нулю, а коефіцієнт реакції, Q _r, дорівнює

\[Q_r = \left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=0 \nonumber\]

У міру розчинення твердого речовини концентрації цих іонів збільшуються, але Q _r залишається меншим, ніж K _sp. Досягаємо рівноваги і «задовольняємо продукт розчинності», коли Q _r = K _sp.

Почнемо з написання реакції рівноваги та виразу продукту розчинності для Pb (IO ₃) ₂.

\[\mathrm{Pb}\left(\mathrm{IO}_{3}\right)_{2}(s)\rightleftharpoons \mathrm{Pb}^{2+}(a q)+2 \mathrm{IO}_{3}^{-}(a q) \nonumber\]

е \[K_{\mathrm{sp}}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \label{6.1}\]

У міру розчинення Pb (IO ₃) ₂ для кожного\(\text{IO}_3^-\) іона Pb ^{2 +} утворюється два іони. Якщо припустити, що зміна молярної концентрації Pb ^{2 +} при рівновазі дорівнює х, то зміна молярної концентрації\(\text{IO}_3^-\) становить 2 х. Наступна таблиця допомагає нам відстежувати початкові концентрації, зміну кон-центрацій та рівноважні концентрації Pb2+ і\(\text{IO}_3^-\).

концентрацій	Пб (ІО 3) 2 (и)	\(\rightleftharpoons\)	Пб ^2 ^+ (ак)	+	2\(\text{IO}_3^-\) (кв)
ініціал	твердий	\ (\ правий лівий гарпуни\) ">	0		\ (\ текст {IO} _3^-\) (aq) ">0
змінити	твердий	\ (\ правий лівий гарпуни\) ">	+ х		\ (\ текст {IO} _3^-\) (aq) ">+ 2 x
рівноваги	твердий	\ (\ правий лівий гарпуни\) ">	х		\ (\ текст {IO} _3^-\) (aq) ">2 x

Оскільки тверда речовина, така як Pb (IO ₃) ₂, не з'являється у вираженні розчинності продукту, нам не потрібно відстежувати його концентрацію. Пам'ятайте, однак, що значення K _sp застосовується лише в тому випадку, якщо в рівновазі присутній якийсь твердий Pb (IO ₃) ₂.

Підставляємо рівноважні концентрації на рівняння\ ref {6.1} і розв'язуємо

\[(x)(2 x)^{2}=4 x^{3}=2.5 \times 10^{-13} \nonumber\]

\[x=3.97 \times 10^{-5} \nonumber\]

Підставляючи це значення x назад у вирази рівноважної концентрації для Pb ^{2 +} і\(\text{IO}_3^-\) дає їх концентрації як

\[\left[\mathrm{Pb}^{2+}\right]=x=4.0 \times 10^{-5} \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=7.9 \times 10^{-5} \nonumber\]

Оскільки один моль Pb (IO ₃) ₂ містить один моль Pb ^{2 +}, молярна розчинність Pb (IO ₃) ₂ дорівнює концентрації Pb ^{2 +}, або\(4.0 \times 10^{-5}\) M.

Ми можемо виразити розчинність сполуки двома способами: як її молярна розчинність (моль/л) або як розчинність маси (г/л). Обов'язково висловлюйте свою відповідь чітко.

Вправа Template:index

Обчисліть молярну розчинність і розчинність маси для Hg ₂ Cl ₂, враховуючи наступну реакцію розчинності і значення K _sp.

\[\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)\rightleftharpoons \mathrm{Hg}_{2}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \quad K_{\mathrm{sp}}=1.2 \times 10^{-8} \nonumber\]

Відповідь

Коли Hg ₂ Cl ₂ розчиняється, два Cl ^— виробляються для кожного іона\(\text{Hg}_2^{2+}\). Якщо припустити х - це зміна молярної концентрації\(\text{Hg}_2^{2+}\), то зміна молярної концентрації Cl ^— 2 х. Наступна таблиця допомагає нам відстежувати наше рішення цієї проблеми.

концентрація	Hg 2 Сл 2 (и)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\)(aq)	+	Cl ^— (aq)
ініціал	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) ">0		0
змінити	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) ">+ x		+2 х
рівноваги	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) "> x		2 х

Підстановка рівноважних концентрацій в експресію K _sp дляHG ₂ Cl ₂ дає

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(2 \mathrm{x})^{2}=4 x^{3}=1.2 \times 10^{-18} \nonumber\]

\[x=6.69 \times 10^{-7} \nonumber\]

Підставляючи x назад у вирази рівноваги для\(\text{Hg}_2^{2+}\) і Cl ^- дає їх концентрації як

\[\left[\mathrm{Hg}_{2}^{2+}\right]=x=6.7 \times 10^{-7} \ \mathrm{M} \quad\left[\mathrm{Cl}^{-}\right]=2 x=1.3 \times 10^{-6} \ \mathrm{M} \nonumber\]

Молярна розчинність дорівнює [\(\text{Hg}_2^{2+}\)], або\(6.7 \times 10^{-7}\) моль/л.

Більш складна проблема: загальний іонний ефект

Розрахунок розчинності Pb (IO ₃) ₂ в деіонізованій воді є простою проблемою, оскільки розчинення твердої речовини є єдиним джерелом Pb ^{2 +} і\(\text{IO}_3^-\). Але що робити, якщо ми додамо Pb (IO ₃) ₂ до розчину 0,10 М Pb (NO ₃) ₂? Перш ніж ми налаштуємо та вирішимо цю проблему алгебраїчно, подумайте про хімію системи та вирішіть, чи збільшиться, зменшиться чи залишиться розчинність Pb (IO ₃) ₂. Початок проблеми, думаючи про ймовірну відповідь - це хороша звичка для розвитку. Знання того, які відповіді є розумними, допоможе вам виявити помилки у ваших розрахунках і дасть вам більше впевненості, що ваше рішення проблеми є правильним. Оскільки рішення вже містить джерело Pb ^{2 +}, ми можемо використовувати принцип Le ChaTelier, щоб передбачити, що розчинність Pb (IO ₃) ₂ менша, ніж у нашій попередній задачі.

Ми починаємо з створення таблиці, щоб допомогти нам відстежувати концентрації Pb ^{2 +} і\(\text{IO}_3^-\) як ця система рухається до і досягає рівноваги.

концентрацій	Пб (ІО 3) 2 (и)	\(\rightleftharpoons\)	Пб ^2 ^+ (ак)	+	2\(\text{IO}_3^-\) (кв)
ініціал	твердий	\ (\ правий лівий гарпуни\) ">	0,10		\ (\ текст {IO} _3^-\) (aq) ">0
змінити	твердий	\ (\ правий лівий гарпуни\) ">	+ х		\ (\ текст {IO} _3^-\) (aq) ">+ 2 x
рівноваги	твердий	\ (\ правий лівий гарпуни\) ">	0,10 х		\ (\ текст {IO} _3^-\) (aq) ">2 x

Підстановка рівноважних концентрацій на рівняння\ ref {6.1}

\[(0.10+x)(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]

і множення членів на лівій стороні рівняння залишає нас

\[4 x^{3}+0.40 x^{2}=2.5 \times 10^{-13} \label{6.2}\]

Це більш складне рівняння для вирішення, ніж для розчинності Pb (IO ₃) ₂ в деіонізованій воді, і його рішення не відразу очевидно. Ми можемо знайти суворе рішення Equation\ ref {6.2} за допомогою обчислювальних програмних пакетів і електронних таблиць, деякі з яких описані в розділі 6.10.

Існує кілька підходів до вирішення кубічних рівнянь, але жоден з них не є обчислювально-простим, використовуючи лише папір та олівець.

Як ми можемо вирішити Equation\ ref {6.2}, якщо у нас немає доступу до комп'ютера? Одним з підходів є використання нашого розуміння хімії для спрощення проблеми. З принципу Le ChaTelier ми знаємо, що велика початкова концентрація Pb ²⁺ значно зменшить розчинність Pb (IO ₃) ₂. Одне розумне припущення полягає в тому, що початкова концентрація Pb ^{2 +} дуже близька до його рівноважної концентрації. Якщо це припущення вірне, то доцільно наступне наближення

\[\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \nonumber\]

Підставляючи це наближення до рівняння\ ref {6.1} та розв'язування для x дає

\[(0.10)(2 x)^{2}=0.4 x^{2}=2.5 \times 10^{-13} \nonumber\]

\[x=7.91 \times 10^{-7} \nonumber\]

Перш ніж прийняти цю відповідь, ми повинні переконатися, що наше наближення є розумним. Різниця між фактичною концентрацією Pb ^{2 +}, яка дорівнює 0,10+ х М, і нашим припущенням, що концентрація Pb ^{2 +} дорівнює 0,10 М дорівнює\(7.9 \times 10^{-7}\), або\(7.9 \times 10^{-4}\)% від передбачуваної концентрації. Це мізерно мала помилка. Якщо прийняти результат нашого розрахунку, то виявимо, що рівноважні концентрації Pb ^{2 +} і\(\text{IO}_3^-\) складають

\[\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=1.6 \times 10^{-6} \ \mathrm{M} \nonumber\]

\[\begin{aligned} \% \text { error } &=\frac{\text { actual }-\text { assumed }}{\text { assumed }} \times 100 \\ &=\frac{(0.10+x)-0.10}{0.10} \times 100 \\ &=\frac{7.91 \times 10^{-7}}{0.10} \times 100 \\ &=7.91 \times 10^{-4} \% \end{aligned} \nonumber\]

Молярна розчинність Pb (IO ₃) ₂ дорівнює додатковій концентрації Pb ^{2 +} в розчині, або\(7.9 \times 10^{-4}\) моль/л Як і очікувалося, виявляємо, що Pb (IO ₃) ₂ менш розчинний в присутності розчину, який вже містить один з його іони. Це відоме як загальний іонний ефект.

Як зазначено в наступному прикладі, якщо наближення призводить до помилки, яка є неприпустимо великою, то ми можемо продовжити процес складання та оцінки наближень.

Одне «емпіричне правило» при складанні наближення полягає в тому, що воно не повинно вводити похибку більше ± 5%. Хоча це не необгрунтований вибір, важливо те, що помилка має сенс у контексті проблеми, яку ви вирішуєте.

Приклад Template:index

Обчисліть розчинність Pb (IO ₃) ₂ в\(1.0 \times 10^{-4}\) M Pb (NO ₃) ₂.

Рішення

Якщо дозволити х дорівнює зміні концентрації Pb ²⁺, то рівноважні концентрації Pb ^{2 +} і\(\text{IO}_3^-\) складають

\[\left[\mathrm{P} \mathrm{b}^{2+}\right]=1.0 \times 10^{-4}+ \ x \text { and }\left[\mathrm{IO}_{3}^-\right]=2 x \nonumber\]

Підставляючи ці концентрації в Equation\ ref {6.1}, ми залишаємо нам

\[\left(1.0 \times 10^{-4}+ \ x\right)(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]

Щоб вирішити це рівняння для x, зробимо наступне припущення

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x \approx 1.0 \times 10^{-4} \ \mathrm{M} \nonumber\]

Розв'язування для x дає його значення як\(2.50 \times 10^{-5}\); однак, коли ми підставляємо це значення на x назад, ми виявляємо, що розрахункова концентрація Pb ²⁺ при рівновазі

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.0 \times 10^{-4}+ \ 2.50 \times 10^{-5}=1.25 \times 10^{-4} \ \mathrm{M} \nonumber\]

на 25% більше, ніж наше припущення\(1.0 \times 10^{-4}\) М. Ця помилка невиправдано велика.

Замість того, щоб кричати в розчаруванні, давайте зробимо нове припущення. Наше перше припущення - що концентрація Pb ^{2 +} є\(1.0 \times 10^{-4}\) M - було занадто малим. Розрахункова концентрація\(1.25 \times 10^{-4}\) M, отже, ймовірно, занадто велика, але ближче до правильної концентрації, ніж було нашим першим припущенням. Для нашого другого наближення припустимо, що

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.25 \times 10^{-4} \mathrm{M} \nonumber\]

Підставляючи в рівняння\ ref {6.1} і розв'язування для x дає його значення як\(2.24 \times 10^{-5}\). Отримана концентрація Pb ^{2 +} становить

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ 2.24 \times 10^{-5}=1.22 \times 10^{-4} \ \mathrm{M} \nonumber\]

який відрізняється від нашого припущення\(1.25 \times 10^{-4}\) М на 2,4%. Оскільки початкова концентрація Pb ^{2 +} дається двом значущим показникам, це більш розумна помилка. Наше остаточне рішення, до двох значущих цифр,

\[\left[\mathrm{Pb}^{2+}\right]=1.2 \times 10^{-4} \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}\right]=4.5 \times 10^{-5} \ \mathrm{M} \nonumber\]

і молярна розчинність Pb (IO ₃) ₂ становить\(2.2 \times 10^{-5}\) моль/л Цей ітераційний підхід до розв'язання задач відомий як метод послідовних наближень.

Вправа Template:index

Обчисліть молярну розчинність для Hg ₂ Cl ₂ в 0,10 М NaCl і порівняйте свою відповідь з його молярною розчинністю в деіонізованій воді (див. Вправа Template:index).

Відповідь

Ми починаємо з створення таблиці, щоб допомогти нам відстежувати концентрації\(\text{Hg}_2^{2+}\) і Cl ^- як ця система рухається в напрямку і досягає рівноваги.

концентрація	Hg 2 Сл 2 (и)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\)(aq)	+	Cl ^— (aq)
ініціал	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) ">0		0,10
змінити	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) ">+ x		+2 х
рівноваги	твердий	\ (\ правий лівий гарпуни\) ">	\ (\ текст {Hg} _2^ {2+}\) (aq) "> x		0,1 + 2 х

Підстановка рівноважних концентрацій в експресію K _sp для Hg ₂ Cl ₂ залишає нам складне для розв'язання кубічне рівняння.

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10+2 x)^{2}=4 x^{3}+0.40 x^{2}+0.010 x \nonumber\]

Давайте зробимо припущення, щоб спростити цю проблему. Тому що ми очікуємо, що значення х буде невеликим, давайте припустимо, що

\[\left[\mathrm{Cl}^{-}\right]=0.10+2 x \approx 0.10 \nonumber\]

Це спрощує нашу проблему

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10)^{2}=0.010 x=1.2 \times 10^{-18} \nonumber\]

що дає значення х як\(1.2 \times 10^{-16}\) М. Різниця між фактичною концентрацією Cl ^—, яка становить (0,10 + 2 х) М, і наше припущення, що вона дорівнює 0,10 М, вводить похибку\(2.4 \times 10^{-13}\)%. Це мізерно мала помилка. Молярна розчинність Hg ₂ Cl ₂ така ж, як і концентрація\(\text{Hg}_2^{2+}\), або\(1.2 \times 10^{-16}\) М. Як і очікувалося, молярна розчинність в 0,10 М NaCl менше\(6.7 \times 10^{-7}\) моль/л, що є його розчинністю у воді (див. Розчин вправи Template:index).

Системний підхід до вирішення задач рівноваги

Розрахунок розчинності Pb (IO ₃) ₂ в розчині Pb (NO ₃) ₂ складніше, ніж розрахунок його розчинності в деіонізованій воді. Однак розрахунок все ще відносно легко організувати, а спрощуючі припущення досить очевидні. Ця проблема досить проста, оскільки передбачає лише одну реакцію рівноваги та одну константу рівноваги.

Визначення рівноважного складу системи з множинними реакціями рівноваги є більш складним. У цьому розділі ми впроваджуємо системний підхід до постановки та вирішення задач рівноваги. Як показано в таблиці Template:index, цей підхід включає чотири кроки.

Таблиця Template:index. Системний підхід до вирішення задач рівноваги

Крок 1 Напишіть всі відповідні реакції рівноваги та вирази постійної рівноваги.

Крок 2 Підрахуйте унікальні види, які з'являються в постійних виразах рівноваги; це ваші невідомі. У вас достатньо інформації для вирішення задачі, якщо кількість невідомих дорівнює числу постійних виразів рівноваги. Якщо ні, додайте рівняння балансу маси та/або рівняння балансу заряду. Продовжуйте додавати рівняння до тих пір, поки кількість рівнянь не дорівнює кількості невідомих.

Крок 3 Об'єднайте свої рівняння і вирішуйте для одного невідомого. По можливості спрощуйте алгебру, зробивши відповідні припущення. Якщо ви зробите припущення, встановіть ліміт на його похибку. Це рішення впливає на вашу оцінку припущення.

Крок 4 Перевірте свої припущення. Якщо будь-яке припущення виявиться недійсним, поверніться до попереднього кроку і продовжуйте рішення. Проблема завершена, коли у вас є відповідь, яка не порушує жодного з ваших припущень.

Крім постійних виразів рівноваги, два інших рівняння важливі для цього системного підходу до вирішення задачі рівноваги. Перше з цих рівнянь - рівняння балансу маси, яке просто є твердженням про те, що речовина зберігається під час хімічної реакції. У розчині оцтової кислоти, наприклад, комбіновані концентрації кон'югату слабкої кислоти СН ₃ СООН і кон'югату слабкої основи СН ₃ СОО ^— повинні дорівнювати початковій концентрації оцтової кислоти,\(C_{\text{CH}_3\text{COOH}}\).

\[C_{\mathrm{CH}_{\mathrm{3}} \mathrm{COOH}}=\left[\mathrm{CH}_{3} \mathrm{COOH}\right]+\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right] \nonumber\]

Ви можете згадати з глави 2, що це різниця між формальною концентрацією та молярною концентрацією. Змінна С являє собою формальну концентрацію.

Друге рівняння - рівняння балансу заряду, яке вимагає, щоб сумарний позитивний заряд від катіонів дорівнював загальному негативному заряду від аніонів. Математично рівняння балансу заряду дорівнює

\[\sum_{i=1}^{n}\left(z^{+}\right)_{i}\left[{C^{z}}^+\right]_{i} = -\sum_{j=1}^{m}(z^-)_{j}\left[{A^{z}}^-\right]_{j} \nonumber\]

де [C ^{z +}] _i і [A ^{z -}] _j - це, відповідно, концентрації ^i-го катіону і j ^го аніону, і ( z ⁺) _i і (z ^—) _j - це заряди для них i ^го катіону та j ^th аніон. Кожен іон в розчині, навіть якщо він не проявляється в реакції рівноваги, повинен з'явитися в рівнянні балансу заряду. Наприклад, рівняння балансу заряду для водного розчину Ca (NO ₃) ₂ дорівнює

\[2 \times\left[\mathrm{Ca}^{2+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{+}\right]+\left[\mathrm{NO}_{3}^-\right] \nonumber\]

Зверніть увагу, що ми помножимо концентрацію Са ²⁺ на два і що включаємо концентрації H ₃ O ⁺ і OH ^—.

Баланс заряду - це збереження заряду. Знак мінус перед терміном підсумовування в правій частині рівняння балансу заряду гарантує, що обидва підсумовування є позитивними. Бувають ситуації, коли неможливо записати рівняння балансу заряду, оскільки ми не маємо достатньої кількості інформації про склад рішення. Наприклад, припустимо, що ми фіксуємо рН розчину за допомогою буфера. Якщо склад буфера не вказано, ми не можемо записати рівняння балансу заряду.

Приклад Template:index

Запишіть рівняння балансу маси та рівняння балансу заряду для 0,10 М розв'язку NaHCO ₃.

Рішення

Простіше відстежувати види в розчині, якщо записати реакції, що визначають склад розчину. Ці реакції являють собою розчинення розчинної солі.

\[\mathrm{NaHCO}_{3}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{HCO}_{3}^{-}(a q) \nonumber\]

і кислотно-лужні реакції дисоціації\(\text{HCO}_3^-\) і H ₂ O

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CO}_{3}^{2-}(a q) \nonumber\]

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{CO}_{3}(a q) \nonumber\]

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Рівняння балансу маси

\[0.10 \mathrm{M}=\left[\mathrm{H}_{2} \mathrm{CO}_{3}\right]+\left[\mathrm{HCO}_{3}^{-}\right]+\left[\mathrm{CO}_{3}^{2-}\right] \nonumber\]

\[0.10 \ \mathrm{M}=\left[\mathrm{Na}^{+}\right] \nonumber\]

і рівняння балансу заряду

\[\left[\mathrm{Na}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{HCO}_{3}^-\right]+2 \times\left[\mathrm{CO}_{3}^{2-}\right] \nonumber\]

Вправа Template:index

Напишіть відповідні рівняння балансу маси і заряду для розчину, що містить 0,10 М KH ₂ PO ₄ і 0,050 M Na ₂ HPO ₄.

Відповідь

Щоб допомогти нам визначити, які іони знаходяться в розчині, запишемо всі реакції, необхідні для приготування розчинів, і реакції рівноваги, що відбуваються всередині цих розчинів. Ці реакції являють собою розчинення двох розчинних солей.

\[\mathrm{KH}_{2} \mathrm{PO}_{4}(s) \longrightarrow \mathrm{K}^{+}(a q)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]

\[\mathrm{NaHPO}_{4}(s) \longrightarrow \mathrm{Na}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber\]

і кислотно-лужні реакції дисоціації для\(\text{H}_2\text{PO}_4^-\),\(\text{HPO}_4^{2-}\). і H ₂ O.

\[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber\]

\[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{3} \mathrm{PO}_{4}(a q) \nonumber\]

\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{PO}_{4}^{3-}(a q) \nonumber\]

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Зауважте, що ми не включили реакцію базової дисоціації,\(\text{HPO}_4^{2-}\) оскільки ми вже враховували її продукт\(\text{H}_2\text{PO}_4^-\), в іншій реакції. Рівняння балансу маси для K ⁺ і Na ⁺ прості

\[\left[\mathrm{K}^{+}\right]=0.10 \ \mathrm{M} \text { and }\left[\mathrm{Na}^{+}\right]=0.10 \ \mathrm{M} \nonumber\]

але рівняння балансу маси для фосфату займає трохи більше думки. Обидва\(\text{H}_2\text{PO}_4^-\) і\(\text{HPO}_4^{2-}\) виробляють однакові іони в розчині. Отже, ми можемо уявити, що рішення спочатку містить 0,15 М KH ₂ PO ₄, що дає наступне рівняння балансу маси.

\[\left[\mathrm{H}_{3} \mathrm{PO}_{4}\right]+\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]+\left[\mathrm{HPO}_{4}^{2-}\right]+\left[\mathrm{PO}_{4}^{3-}\right]=0.15 \ \mathrm{M} \nonumber\]

Рівняння балансу заряду дорівнює

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{K}^{+}\right]+\left[\mathrm{Na}^{+}\right] =\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]+2 \times\left[\mathrm{HPO}_{4}^{2-}\right] +3 \times\left[\mathrm{PO}_{4}^{3-}\right]+\left[\mathrm{OH}^{-}\right] \nonumber\]

рН монопротонної слабкої кислоти

Для ілюстрації системного підходу до вирішення задач рівноваги обчислимо рН 1,0 М ВЧ. Дві реакції рівноваги впливають на рН. Першою, і найбільш очевидною, є реакція дисоціації кислоти для HF

\[\mathrm{HF}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \nonumber\]

для яких постійне вираження рівноваги

\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=6.8 \times 10^{-4} \label{6.3}\]

Друга реакція рівноваги - дисоціація води, що є очевидною, але легко занедбаною реакцією.

\[2 \mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.4}\]

Підраховуючи невідомі, знаходимо чотири: [HF], [F ^—], [H ₃ O ⁺], і [ОН ^—]. Для вирішення цієї задачі нам знадобляться два додаткових рівняння. Ці рівняння є рівнянням балансу мас на плавиковій кислоті

\[C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]=1.0 \mathrm{M} \label{6.5}\]

і рівняння балансу заряду

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{F}^{-}\right] \label{6.6}\]

З чотирма рівняннями і чотирма невідомими ми готові вирішити задачу. Перш ніж це зробити, давайте спростимо алгебру, зробивши два припущення.

Припущення одне. Оскільки HF - це слабка кислота, ми знаємо, що розчин кислий. Для кислого розчину розумно припустити, що

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]>>\left[\mathrm{OH}^{-}\right] \nonumber\]

що спрощує рівняння балансу заряду

\[C_{\mathrm{HF}}=[\mathrm{HF}]=1.0 \ \mathrm{M} \label{6.7}\]

Успенська друга. Оскільки HF є слабкою кислотою, дуже мало її дисоціює з утворенням F ^—. Велика частина ВЧ залишається в кон'югатній слабкій кислотній формі і розумно припустити, що

\[[\mathrm{HF}]>>\left[\mathrm{F}^{-}\right] \nonumber\]

що спрощує рівняння балансу маси до

\[C_{\mathrm{HF}}=[\mathrm{HF}]=1.0 \ \mathrm{M} \label{6.8}\]

Для цієї вправи приймемо припущення, якщо воно вводить похибку менше ± 5%.

Заміна рівняння\ ref {6.7} та рівняння\ ref {6.8} на рівняння\ ref {6.3} та розв'язування концентрації H ₃ O ⁺ дає нам

\[\mathrm{K}_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\mathrm{C}_{\mathrm{HF}}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{\mathrm{C}_{\mathrm{HF}}}=6.8 \times 10^{-4} \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} C_{\mathrm{HF}}}=\sqrt{\left(6.8 \times 10^{-4}\right)(1.0)}=2.6 \times 10^{-2} \nonumber\]

Перш ніж прийняти цю відповідь, ми повинні перевірити наші припущення. Перше припущення полягає в тому, що [ОН ^—] значно менше, ніж [H ₃ O ⁺]. Використовуючи рівняння\ ref {6.4}, ми знаходимо, що

\[\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{1.00 \times 10^{-14}}{2.6 \times 10^{-2}}=3.8 \times 10^{-13} \nonumber\]

Очевидно, що це припущення є прийнятним. Друге припущення полягає в тому, що [F ^—] значно менше, ніж [HF]. З рівняння\ ref {6.7} ми маємо

\[\left[\mathrm{F}^{-}\right]=2.6 \times 10^{-2} \ \mathrm{M} \nonumber\]

Оскільки [F ^—] становить 2,60% від C _HF, це припущення також є прийнятним. З огляду на, що [Н ₃ О ⁺] дорівнює\(2.6 \times 10^{-2}\) М, рН 1,0 М ВЧ дорівнює 1,59.

Як змінюється розрахунок, якщо ми вимагаємо, щоб похибка, введена в наших припущеннях, була менше ± 1%? У цьому випадку ми вже не можемо вважати, що [HF] >> [F ^—] і ми не можемо спростити рівняння балансу маси. Розв'язування рівняння балансу маси для [HF]

\[[\mathrm{HF}]=C_{\mathrm{HF}}-\left[\mathrm{F}^{-}\right]=C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]

_{і підставляючи до K вираз разом з Equation\ ref {6.7} дає}

\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

Перевпорядкування цього рівняння залишає нам квадратне рівняння

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}+K_{\mathrm{a}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-K_{\mathrm{a}} C_{\mathrm{HF}}=0 \nonumber\]

яку ми вирішуємо за допомогою квадратичної формули

\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber\]

де a, b і c - коефіцієнти в квадратному рівнянні

\[a x^{2}+b x+c=0 \nonumber\]

Розв'язування квадратного рівняння дає два кореня, тільки один з яких має хімічне значення. Для нашої задачі коріння рівняння

\[x=\frac{-6.8 \times 10^{-4} \pm \sqrt{\left(6.8 \times 10^{-4}\right)^{2}-(4)(1)\left(-6.8 \times 10^{-4}\right)}}{(2)(1)} \nonumber\]

\[x=\frac{-6.8 \times 10^{-4} \pm 5.22 \times 10^{-2}}{2} \nonumber\]

\[x=2.57 \times 10^{-2} \text { or }-2.64 \times 10^{-2} \nonumber\]

Тільки позитивний корінь є хімічно значущим, оскільки негативний корінь дає негативну концентрацію для Н ₃ О ⁺. Таким чином, [Н ₃ О ⁺] дорівнює\(2.57 \times 10^{-2}\) М, а рН - 1,59.

Ви можете розширити цей підхід до обчислення рН монопротного слабкої основи, замінивши K _a на K _b, замінивши C _HF на концентрацію слабкої основи та розв'язавши для [ОН ^—] замість [H ₃ O ⁺ ].

Вправа Template:index

Обчисліть рН 0,050 М NH ₃. Викладіть будь-які припущення, які ви робите при вирішенні проблеми, обмежуючи похибку для будь-якого припущення ± 5%. Значення K _b для NH ₃ дорівнює\(1.75 \times 10^{-5}\).

Відповідь

Щоб визначити рН 0,050 М NH ₃, потрібно розглянути дві реакції рівноваги: реакцію дисоціації основи для NH ₃

\[\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q) \nonumber\]

і реакція дисоціації води.

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Ці дві реакції містять чотири види, концентрації яких нам потрібно враховувати: NH ₃\(\text{NH}_4^+\), H ₃ O ⁺ та OH ^-. Для розв'язання задачі нам потрібні чотири рівняння - це рівняння K _b для NH ₃

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \nonumber\]

рівняння K _w для H ₂ O

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]

рівняння балансу маси на аміаку

\[C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right] \nonumber\]

і рівняння балансу заряду

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber\]

Щоб вирішити цю проблему, зробимо два припущення. Оскільки NH ₃ є базою, наше перше припущення

\[\left[\mathrm{OH}^{-}\right]>>\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]

що спрощує рівняння балансу заряду

\[\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber\]

Оскільки NH ₃ є слабкою базою, наше друге припущення

\[\left[\mathrm{NH}_{3}\right]>>\left[\mathrm{NH}_{4}^{+}\right] \nonumber\]

що спрощує рівняння балансу маси до

\[C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right] \nonumber\]

Підставляючи спрощене рівняння балансу заряду та рівняння балансу маси в рівняння K _b, залиште нам

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{OH}^{-}\right]}{C_{\mathrm{NH}_3}}=\frac{\left[\mathrm{OH}^{-}\right]^{2}}{C_{\mathrm{NH_3}}}=1.75 \times 10^{-5} \nonumber\]

\[\left[\mathrm{OH}^{-}\right]=\sqrt{K_{\mathrm{b}} C_{\mathrm{NH_3}}}=\sqrt{\left(1.75 \times 10^{-5}\right)(0.050)}=9.35 \times 10^{-4} \nonumber\]

Перш ніж прийняти цю відповідь, ми повинні перевірити наші два припущення. Перше припущення полягає в тому, що концентрація ОН ^— значно перевищує концентрацію Н ₃ О ⁺. Використовуючи K _w, ми знаходимо, що

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{9.35 \times 10^{-4}}=1.07 \times 10^{-11} \nonumber\]

Очевидно, що це припущення є прийнятним. Наше друге припущення полягає в тому, що концентрація NH ₃ значно перевищує концентрацію\(\text{NH}_4^+\). Використовуючи наше спрощене рівняння балансу заряду, ми знаходимо, що

\[\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right]=9.35 \times 10^{-4} \nonumber\]

Оскільки концентрація\(\text{NH}_4^+\) становить 1,9%\(C_{\text{NH}_3}\), наше друге припущення також є розумним. З огляду на, що [Н ₃ О ⁺] є\(1.07 \times 10^{-11}\), рН дорівнює 10,97.

рН поліпротової кислоти або основи

Більш складною проблемою є пошук рН розчину, який містить поліпротонную слабку кислоту або один з її кон'югатних видів. Як приклад розглянемо амінокислоту аланін, структура якої показана на малюнку Template:index. Діаграма сходів на малюнку Template:index показує три кислотно-основні форми аланіну та відповідні області переважання. Для простоти виділимо ці види як H ₂ L ⁺, HL і L ^—.

Рисунок Template:index. Структура амінокислоти аланін, що має р К а значення 2,348 (—СООН) і 9,867 (—NH 2).

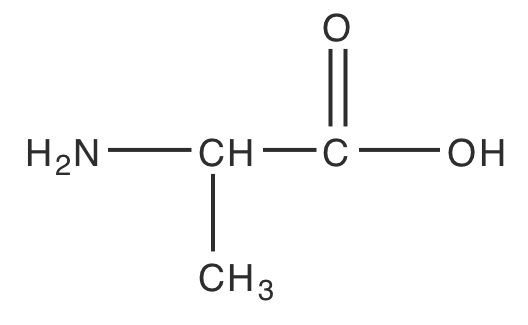
Рисунок Template:index. Схема сходів для аланіна.

рН 0,10 М аланін гідрохлорид (H ₂ L ⁺)

Аланін гідрохлорид є сіллю дипротової слабкої кислоти H ₂ ^L+ і Cl ^-. Оскільки Н ₂ L ⁺ має дві реакції дисоціації кислоти, повне систематичне рішення цієї проблеми складніше, ніж для монопротонной слабкої кислоти. Діаграма сходів на малюнку Template:index допомагає нам спростити проблему. Оскільки ділянки переважання для H ₂ L ⁺ і L ^— настільки далекі один від одного, можна припустити, що розчин Н ₂ L ⁺ не буде містити значної кількості L ^—. В результаті ми можемо лікувати H ₂ L ⁺ так, ніби це монопротонная слабка кислота. Розрахунок рН 0,10 М гідрохлориду аланіну, який становить 1,72, залишається читачеві як вправа.

рН 0,10 М аланінат натрію (L ^-)

Іон аланінату є діпротическим слабкою основою. Оскільки L ^— має дві реакції дисоціації основи, повне систематичне вирішення цієї проблеми складніше, ніж для монопротичного слабкої основи. Знову ж таки, діаграма сходів на малюнку Template:index допомагає нам спростити проблему. Оскільки ділянки переважання для H ₂ L ⁺ і L ^— настільки далекі один від одного, можна припустити, що розчин L ^— не буде містити значної кількості Н ₂ L ⁺. В результаті ми можемо лікувати L ^{— ніби} це монопротна слабка основа. Розрахунок рН 0,10 М аланінату натрію, що становить 11,42, залишається читачеві як вправу.

рН 0,10 М аланін (HL)

Знайти рН розчину аланіну складніше, ніж наші попередні два приклади, оскільки ми не можемо ігнорувати наявність або H ₂ L ⁺, або L ^-. Щоб розрахувати рН розчину, ми повинні розглянути реакцію дисоціації кислоти аланіну

\[\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{L}^{-}(a q) \nonumber\]

і його основна реакція дисоціації

\[\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{L}^{+}(a q) \nonumber\]

і, як завжди, ми також повинні враховувати дисоціацію води

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Це залишає нам п'ять невідомих— [H ₂ L ⁺], [HL], [L ^—], [H ₃ O ⁺], і [OH ^—] —для яких нам потрібно п'ять рівнянь. Цими рівняннями є K _a2 і K _b2 для аланіну.

\[K_{\mathrm{a} 2}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{L}^{-}\right]}{[\mathrm{HL}]} \nonumber\]

\[K_{\mathrm{b} 2}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a1}}}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]}{[\mathrm{HL}]} \nonumber\]

рівняння K _w

\[K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]

рівняння балансу маси для аланіну

\[C_{\mathrm{HL}}=\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{HL}]+[\mathrm{L}^{-}] \nonumber\]

і рівняння балансу заряду

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{L^-}] \nonumber\]

Оскільки HL - це слабка кислота і слабка основа, здається розумним припустити, що мало що буде дисоціювати і що

\[[\mathrm{HL}]>>\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{L}^-] \nonumber\]

що дозволяє нам спростити рівняння балансу маси до

\[C_{\mathrm{HL}}=[\mathrm{HL}] \nonumber\]

Далі вирішуємо K _b2 для [H ₂ L ⁺]

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{K_{\mathrm{w}}[\mathrm{HL}]}{K_{\mathrm{a1}}\left[\mathrm{OH}^{-}\right]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}} \nonumber\]

і вирішити K _a2 для [L ^—]

\[[\mathrm{L^-}]=\frac{K_{a2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

Підставляючи ці рівняння на [H ₂ L ⁺] і [L ^—], і рівняння для K _w, в рівняння зарядового балансу дають нам

\[\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}}+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}+\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

які ми спрощуємо

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left(\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1\right)=\frac{1}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\left(K_{\mathrm{w}}+K_{a2} C_{\mathrm{HL}}\right) \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}=\frac{\left(K_{\mathrm{a} 2} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1}=\frac{K_{\mathrm{a1}}\left(K_{\mathrm{a2}} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}} \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\frac{\left(K_{\mathrm{a1}} K_{a2} C_{\mathrm{HL}}+K_{\mathrm{a1}} K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}}} \nonumber\]

Ми можемо ще більше спростити це рівняння, якщо K _a1 K _w << K _a1 K _a2 C _HL, і якщо K _a1 << C _HL, залишивши нас з

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a1}} K_{\mathrm{a} 2}} \nonumber\]

Для розчину 0,10 М аланіну [H ₃ O ⁺] становить

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\left(4.487 \times 10^{-3}\right)\left(1.358 \times 10^{-10}\right)}=7.806 \times 10^{-7} \ \mathrm{M} \nonumber\]

або рН 6,11.

Вправа Template:index

Переконайтеся, що кожне припущення в нашому розчині для рН 0,10 М аланін є розумним, використовуючи ± 5% як межу допустимої похибки.

Відповідь

У розв'язанні для рН 0,10 М аланіну ми зробили наступні три припущення: (а) [HL] >> [H ₂ L ⁺] + [L ^—]; (b) K _a1 K _w << K _a1 K _a2 C _НЛ; і (с) К _a1 << С _ГЛ. Припущення (b) і (c) легко перевірити. Значення K _a1 (\(4.487 \times 10^{-3}\)) дорівнює 4,5% C _HL (0,10), а K _a1 K w (\(4.487 \times 10^{-17}\)) - 0,074% від К _{a1 К а2} С _HL (\(6.093 \times 10^{-14}\)). Кожне з цих припущень вводить похибку менше ± 5%.

Для перевірки припущення (а) нам потрібно обчислити концентрації H ₂ L ⁺ і L ^—, які ми виконуємо за допомогою рівнянь для K _a1 і K _a2.

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{\left(7.807 \times 10^{-7}\right)(0.10)}{4.487 \times 10^{-3}}=1.74 \times 10^{-5} \nonumber\]

\[\left[\mathrm{L}^{-}\right]=\frac{K_{a 2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{\left(1.358 \times 10^{-10}\right)(0.10)}{7.807 \times 10^{-7}}=1.74 \times 10^{-5} \nonumber\]

Оскільки ці концентрації становлять менше ± 5% від C HL, перше припущення також є прийнятним.

Вплив комплексоутворення на розчинність

Одним із способів підвищення розчинності осаду є додавання ліганду, який утворює розчинні комплекси з одним з іонів осаду. Наприклад, розчинність AgI збільшується в присутності NH ₃ за рахунок утворення розчинного\(\text{Ag(NH}_3)_2^+\) комплексу. Як завершальну ілюстрацію системного підходу до вирішення задач рівноваги обчислимо молярну розчинність AgI в 0,10 М NH ₃.

Почнемо з написання відповідних реакцій рівноваги, які включають розчинність AgI, кислотно-основну хімію NH ₃ та H ₂ O та хімію комплексоутворення металів між Ag ⁺ та NH ₃.

\[\begin{array}{c}{\operatorname{AgI}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{I}^{-}(a q)} \\ {\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)} \\ {\mathrm{Ag}^{+}(a q)+2 \mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}(a q)}\end{array} \nonumber\]

Це залишає нам сім невідомих— [Ag ⁺], [I ^—], [NH ₃\(\text{NH}_4^+\)], [OH ^—], [H ₃ O ⁺], і [\(\text{Ag(NH}_3)_2^+\)] -і необхідність семи рівнянь. Чотири рівняння, які нам потрібні для вирішення цієї задачі, - це вирази постійної рівноваги.

\[K_{\mathrm{sp}}=\left[\mathrm{Ag}^{+}\right]\left[\mathrm{I}^{-}\right]=8.3 \times 10^{-17} \label{6.9}\]

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \label{6.10}\]

\[K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.11}\]

\[\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right]\left[\mathrm{NH}_{3}\right]^{2}}=1.7 \times 10^{7} \label{6.12}\]

Нам ще знадобляться три додаткових рівняння. Перше з цих рівнянь - це баланс маси для NH ₃.

\[C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right]+2 \times\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.13}\]

При написанні цього рівняння балансу маси ми помножимо концентрацію\(\text{Ag(NH}_3)_2^+\) на два, оскільки є два молі NH ₃ на моль\(\text{Ag(NH}_3)_2^+\). Друге додаткове рівняння - це баланс маси між йодидом і сріблом. Оскільки AGI є єдиним джерелом I ^- і Ag ⁺, кожен йодид у розчині повинен мати пов'язаний іон срібла, який може бути Ag ⁺ або\(\text{Ag(NH}_3)_2^+\); таким чином

\[\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.14}\]

Нарешті, ми включимо рівняння балансу заряду.

\[\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{I}^-] \label{6.15}\]

Хоча проблема виглядає складною, три припущення значно спрощують алгебру.

Припущення одне. Оскільки формування\(\text{Ag(NH}_3)_2^+\) комплексу настільки сприятливо (\(\beta_2\)є\(1.7 \times 10^7\)), вільного Ag ⁺ в розчині дуже мало і розумно припустити, що

\[\left[\mathrm{Ag}^{+}\right]<<\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \nonumber\]

Успенська друга. Оскільки NH ₃ є слабкою основою, ми можемо обґрунтовано припустити, що більшість некомплексного аміаку залишається як NH ₃; таким чином

\[\left[\mathrm{NH}_{4}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber\]

Успіння третє. Оскільки K _sp для AgI значно менший, ніж\(\beta_2\) для\(\text{Ag(NH}_3)_2^+\), розчинність AgI, ймовірно, досить мала, що для формування комплексу метал-ліганд потрібно дуже мало аміаку; таким чином

\[\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber\]

Оскільки ми використовуємо ці припущення для спрощення алгебри, давайте встановимо ± 5% як межу для похибки.

Припущення два і припущення три припускають, що концентрація NH ₃ набагато більше, ніж концентрації\(\text{NH}_4^+\) або або\(\text{Ag(NH}_3)_2^+\), що дозволяє спростити рівняння балансу маси для NH ₃ до

\[C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right] \label{6.16}\]

Нарешті, використовуючи припущення, яке говорить про те, що\(\text{Ag(NH}_3)_2^+\) концентрація набагато більша за концентрацію Ag ⁺, ми спростимо рівняння балансу маси для I ^— до

\[\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.17}\]

Тепер ми готові комбінувати рівняння і вирішувати задачу. Ми починаємо з розв'язання рівняння\ ref {6.9} для [Ag ⁺] і підставляємо його на\(\beta_2\) (Equation\ ref {6.12}), що залишає нам

\[\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right][\mathrm{I}^-]}{K_{\mathrm{sp}}\left[\mathrm{NH}_{3}\right]^{2}} \label{6.18}\]

Далі підставляємо рівняння\ ref {6.16} і рівняння\ ref {6.17} в Рівняння\ ref {6.18}, отримуючи

\[\beta_{2}=\frac{\left[\mathrm{I}^{-}\right]^{2}}{K_{\mathrm{sp}}\left(C_{\mathrm{NH}_3}\right)^{2}} \label{6.19}\]

Рішення рівняння\ ref {6.19} для [I ^—] дає

\[\left[\mathrm{I}^{-}\right]=C_{\mathrm{NH}_3} \sqrt{\beta_{2} K_{s p}} = \\ (0.10) \sqrt{\left(1.7 \times 10^{7}\right)\left(8.3 \times 10^{-17}\right)}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber\]

Оскільки один моль AgI виробляє один моль I ^—, молярна розчинність AgI така ж, як і [I ^—], або\(3.8 \times 10^{-6}\) моль/л.

Перш ніж прийняти цю відповідь, нам потрібно перевірити наші припущення. Підставляючи [I ^—] в рівняння\ ref {6.9}, ми виявимо, що концентрація Ag ⁺ дорівнює

\[\left[\mathrm{Ag}^{+}\right]=\frac{K_{\mathrm{p}}}{[\mathrm{I}^-]}=\frac{8.3 \times 10^{-17}}{3.76 \times 10^{-6}}=2.2 \times 10^{-11} \ \mathrm{M} \nonumber\]

Підставляючи концентрації I ^— і Ag+ в рівняння балансу маси для йодиду (Equation\ ref {6.14}), дає концентрацію\(\text{Ag(NH}_3)_2^+\) як

\[\left[\operatorname{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]=[\mathrm{I}^-]-\left[\mathrm{Ag}^{+}\right]=3.76 \times 10^{-6}-2.2 \times 10^{-11}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber\]

Наше перше припущення, що [Ag ⁺] значно менший, ніж [\(\text{Ag(NH}_3)_2^+\)], є розумним.

Підставляючи концентрації Ag ⁺ і\(\text{Ag(NH}_3)_2^+\) в рівняння\ ref {6.12} і розв'язуючи для [NH ₃], дає

\[\left[\mathrm{NH}_{3}\right]=\sqrt{\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right] \beta_{2}}}=\sqrt{\frac{3.76 \times 10^{-6}}{\left(2.2 \times 10^{-11}\right)\left(1.7 \times 10^{7}\right)}}=0.10 \ \mathrm{M} \nonumber\]

З рівняння балансу маси для NH3 (Equation\ ref {6.12}) ми бачимо, що [\(\text{NH}_4^+\)] є незначним, перевіряючи наше друге припущення,\([\text{NH}_4^+]\) яке значно менше, ніж [NH ₃]. Наше третє припущення, що [\(\text{Ag(NH}_3)_2^+\)] значно менший, ніж [NH ₃], також є розумним.

Ви помітили, що наше рішення цієї проблеми не використовувало рівняння балансу заряду Equation\ ref {6.15}? Причина цього в тому, що ми не намагалися вирішити для концентрації всіх семи видів. Якщо нам потрібно знати повний склад реакційної суміші при рівновазі, то нам потрібно буде включити рівняння балансу заряду в наше рішення.