6.8: Буферні розчини
- Page ID
- 24928
Додавання всього лише 0,1 мл концентрованого HCl до літра H 2 O зміщує рН від 7,0 до 3,0. Додавання такої ж кількості HCl до літра розчину, що 0,1 М в оцтовій кислоті і 0,1 М в ацетаті натрію, однак призводить до незначної зміни рН. Чому ці два рішення так по-різному реагують на додавання HCl?
Суміш оцтової кислоти та ацетату натрію є одним із прикладів кислотно-основного буфера. Щоб зрозуміти, як цей буфер працює, щоб обмежити зміну рН, нам потрібно розглянути його реакцію дисоціації кислоти.
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
і відповідна їй постійна дисоціації кислоти
Беручи негативний журнал термінів у Equation\ ref {6.1} та розв'язуючи pH, ми отримуємо результат, показаний тут.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]
Ви можете згадати, що ці самі рівняння ми розробили в розділі 6.6, коли ми вводили діаграми сходів.
Буферизація відбувається через логарифмічну залежність між рН і співвідношенням концентрації ацетату і оцтової кислоти. Ось приклад, щоб проілюструвати цей момент. Якщо концентрації оцтової кислоти і ацетату рівні, рН буфера дорівнює 4,76. Якщо перетворити 10% ацетату в оцтову кислоту, додаючи сильну кислоту, співвідношення [CH 3 COO —]/[CH 3 COOH] змінюється з 1,00 до 0,818, а рН зменшується з 4,76 до 4,67 — зменшення лише на 0,09 одиниць рН.
Співвідношення [CH 3 COO -]/[CH 3 COOH] стає 0,9/1,1 = 0,818 і рН стає
\[\mathrm{pH}=4.76+\log (0.818)=4.67 \nonumber\]
Систематичне рішення буферних проблем
Рівняння\ ref {6.2} записано через рівноважні концентрації СН 3 СООН та СН 3 СОО —. Більш корисна залежність пов'язує рН буфера до початкових концентрацій слабкої кислоти і слабкої основи. Ми можемо отримати загальне буферне рівняння, розглянувши наступні реакції для слабкої кислоти, HA та розчинної солі її кон'югатної слабкої основи, NaA.
\[\begin{array}{c}{\mathrm{NaA}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {\mathrm{HA}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)}\end{array} \nonumber\]
Оскільки концентрації Na +, A —, HA, H 3 O + та OH — невідомі, нам потрібно п'ять рівнянь для визначення складу розчину. Два з цих рівнянь є вирази постійної рівноваги для HA і H 2 O.
\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]
Решта три рівняння є рівняннями балансу маси для HA і Na +
\[C_{\mathrm{HA}}+C_{\mathrm{NaA}}=[\mathrm{HA}]+\left[\mathrm{A}^{-}\right] \label{6.4}\]
\[C_{\mathrm{NaA}}=\left[\mathrm{Na}^{+}\right] \label{6.5}\]
і рівняння балансу заряду
Підставляючи рівняння\ ref {6.5} на рівняння\ ref {6.6} та розв'язування для [A —] дає
Далі підставляємо рівняння\ ref {6.7} у Рівняння\ ref {6.4}, яке дає концентрацію ГК як
Нарешті, ми замінюємо рівняння\ ref {6.7} та Equation\ ref {6.8} у Рівняння\ ref {6.3} і вирішуємо для pH, щоб прийти до загального рівняння для рН буфера.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA} }-\left[\mathrm{OH}^{-}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{C_{\mathrm{HA}}+\left[\mathrm{OH}^{-}\right]-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]
Якщо початкові концентрації слабкої кислоти, C HA і слабкої основи C NaA. значно більше [H 3 O +] і [OH —], то можна спростити загальне рівняння до Хендерсона— Рівняння Хассельбальха.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA}}}{C_{\mathrm{HA}}} \label{6.9}\]
Як зазначено нижче, рівняння Хендерсона - Хассельбальха забезпечує простий спосіб обчислити рН буфера та визначити зміну рН при додаванні сильної кислоти або сильної основи.
Лоуренс Хендерсон (1878‐1942) вперше розробив зв'язок між [H 3 O +], [HA] та [A —] під час вивчення буферизації крові. Курт Хассельбальх (1874‒1962) модифікував рівняння Гендерсона, перетворивши його в логарифмічну форму, показану в Equation\ ref {6.9}. Припущення, що призводять до Equation\ ref {6.9}, призводять до мінімальної похибки в рН (<± 5%) для більших концентрацій ГК і А -, для концентрацій ГК і А - аналогічних за величиною, і для слабких кислот зі значеннями p K a ближче до 7. Для більшості проблем у цьому підручнику Equation\ ref {6.9} дає прийнятні результати. Будьте впевнені, однак, щоб перевірити свої припущення. Для обговорення рівняння Гендерсона—Хассельбальха, включаючи похибку, властиву рівнянню\ ref {6.9}, див. Po, H.N.; Senozan, N.M. «Рівняння Гендерсона-Хассельбальха: його історія та обмеження», J.Chem. Едук. 2001, 78, 1499—1503.
Обчисліть рН буфера, який становить 0,020 М в NH 3 і 0,030 М в NH 4 Cl. Що таке рН після того, як ми додаємо 1,0 мл 0,10 М NaOH до 0,10 л цього буфера?
Рішення
Константа дисоціації кислоти для\(\text{NH}_4^+\) є\(5.70 \times 10^{-10}\), яка є р К а 9,24. Підставляючи початкові концентрації NH 3 і NH 4 Cl в рівняння\ ref {6.9} і вирішивши, ми виявимо, що рН буфера дорівнює
\[\mathrm{pH}=9.24+\log \frac{0.020}{0.030}=9.06 \nonumber\]
При рН 9,06 концентрація Н 3 О + є\(8.71 \times 10^{-10}\) і концентрація ОН — становить\(1.15 \times 10^{-5}\). Оскільки обидві ці концентрації набагато менші, ніж\(C_{\text{NH}_3}\) або\(C_{\text{NH}_4\text{Cl}}\), наближення, що використовуються для отримання Equation\ ref {6.9}, є розумними.
Додавання NaOH перетворює частину на\(\text{NH}_4^+\) NH 3 наступну реакцію
\[\mathrm{NH}_{4}^{+}(a q)+\mathrm{OH}^{-}(a q) \rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{NH}_{3}(a q) \nonumber\]
Оскільки постійна рівноваги цієї реакції настільки велика (вона дорівнює (K b) -1 або\(5.7 \times 10^4\)), ми можемо розглядати реакцію так, ніби вона йде до завершення. Нові концентрації\(\text{NH}_4^+\) і NH 3 є
\[C_{\mathrm{NH}_{4}^{+}}=\frac{\operatorname{mol} \ \mathrm{NH}_{4}^{+}- \ \mathrm{mol} \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{NH}_4^+}=\frac{(0.030 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.029 \ \mathrm{M} \nonumber\]
\[C_{\mathrm{NH}_{3}}=\frac{\mathrm{mol} \ \mathrm{NH}_{3}+\mathrm{mol} \ \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{NH}_3}=\frac{(0.020 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.021 \ \mathrm{M} \nonumber\]
Підстановка цих концентрацій в рівняння 6.60 дає рН
\[\mathrm{pH}=9.24+\log \frac{0.021}{0.029}=9.10 \nonumber\]
Зверніть увагу, що додавання NaOH збільшує рН з 9,06 до 9,10. Як ми очікуємо, додавання основи робить рН більш основним. Перевірка того, щоб побачити, що рН змінюється в правильному напрямку, є одним із способів зловити помилку розрахунку.
Обчисліть рН буфера, який становить 0,10 М в KH 2 PO 4 і 0,050 М в Na 2 HPO 4. Що таке рН після того, як ми додамо 5,0 мл 0,20 М HCl до 0,10 л цього буфера. Використовуйте Додаток 11, щоб знайти відповідне значення K.
- Відповідь
-
Постійна дисоціації кислоти для\(\text{H}_2\text{PO}_4^-\) є\(6.32 \times 10^{-8}\), або р К а 7.199. Підставляючи початкові концентрації\(\text{H}_2\text{PO}_4^-\) і\(\text{HPO}_4^{2-}\) в Equation\ ref {6.9} і розв'язування дає рН буфера як
\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]}=7.199+\log \frac{0.050}{0.10}=6.898 \approx 6.90\nonumber\]
Додавання HCl перетворює частину\(\text{HPO}_4^{2-}\) до в\(\text{H}_2\text{PO}_4^-\) результаті наступної реакції
\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{3} \mathrm{O}^{+}(a q)\rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]
Оскільки постійна рівноваги цієї реакції настільки велика (вона є\(1.59 \times 10^7\)), ми можемо ставитися до реакції так, ніби вона йде до завершення. Нові концентрації\(\text{H}_2\text{PO}_4^-\) і\(\text{HPO}_4^{2-}\) є
\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{\mathrm{mol} \ \mathrm{H}_{2} \mathrm{PO}_{4}^{-}+\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{(0.10 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.105 \ \mathrm{M} \nonumber\]
\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{\mathrm{mol} \ \mathrm{HPO}_{4}^{2-}-\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{(0.05 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.0381 \ \mathrm{M} \nonumber\]
Заміна цих концентрацій в рівняння\ ref {6.9} дає рН
\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]}=7.199+\log \frac{0.0381}{0.105}=6.759 \approx 6.76 \nonumber\]
Як ми очікуємо, додавання HCl зменшує рН буфера на невелику кількість, знижуючись з 6,90 до 6,76.
Ми можемо використовувати мультипротонну слабку кислоту для приготування буферів при такій кількості різних рН, скільки є кислі протони, при цьому рівняння Хендерсона - Хассельбальха застосовується в кожному випадку. Наприклад, для малонової кислоти (p K a1 = 2,85 і p K a2 = 5,70) ми можемо підготувати буфери зі значеннями рН
\[\begin{array}{l}{\mathrm{pH}=2.85+\log \frac{C_{\mathrm{HM}^{-}}}{C_{\mathrm{H}_{2} \mathrm{M}}}} \\ {\mathrm{pH}=5.70+\log \frac{C_{\mathrm{M}^{2-}}}{C_{\mathrm{HM}^-}}}\end{array} \nonumber\]
де H 2 M, HM - і M 2— є різними кислотно-основними формами малонової кислоти.
Хоча наша обробка буферів базується на кислотно-основній хімії, ми можемо розширити буфери до рівноваг, які включають комплексоутворення або окислювально-відновні реакції. Наприклад, рівняння Нернста для розв'язку, що містить Fe 2 + та Fe 3 +, подібне за формою до рівняння Гендерсона-Хассельбальха.
\[E=E_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{\circ}-0.05916 \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]} \nonumber\]
Розчин, що містить аналогічні концентрації Fe 2 + і Fe 3 +, буферується до потенціалу, близького до стандартного потенціалу відновлення стану для Fe 3 +. Ми називаємо такі рішення окислювально-відновними буферами. Додавання сильного окислювача або сильного відновника до окислювально-відновного буфера призводить до невеликої зміни потенціалу.
Представлення буферних рішень за допомогою діаграм сходів
Схема сходів забезпечує простий спосіб візуалізації переважаючих видів рішення як функції умов рішення. Це також забезпечує зручний спосіб показати діапазон умов розчину, над якими буфер ефективний. Наприклад, кислотно-лужний буфер існує, коли концентрації слабкої кислоти та її кон'югатної слабкої основи подібні. Для зручності припустимо, що кислотно-базовий буфер існує, коли
\[\frac{1}{10} \leq \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \leq \frac{10}{1} \nonumber\]
Підстановка цих співвідношень у рівняння Гендерсона—Хассельбальха
\[\begin{aligned} \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{1}{10}=\mathrm{p} K_{\mathrm{a}}-1 \\ \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{10}{1}=\mathrm{p} K_{\mathrm{a}}+1 \end{aligned} \nonumber\]
показує, що кислотно-основний буфер працює в діапазоні рН p K a ± 1.
Використовуючи той самий підхід, легко показати, що буфер комплексоутворення метал-лігандів для ML n існує, коли
\[\mathrm{pL}=\log K_{n} \pm 1 \text { or } \mathrm{pL}=\log \beta_{n} \pm \frac{1}{n} \nonumber\]
де K n or\(\beta_n\) - відповідна ступінчаста або загальна константа формування. Для окислювача та його кон'югатного відновника існує окислювально-відновний буфер, коли
\[E=E^{\circ} \pm \frac{1}{n} \times \frac{R T}{F}=E^{\circ} \pm \frac{0.05916}{n}\left(\text { at } 25^{\circ} \mathrm{C}\right) \nonumber\]
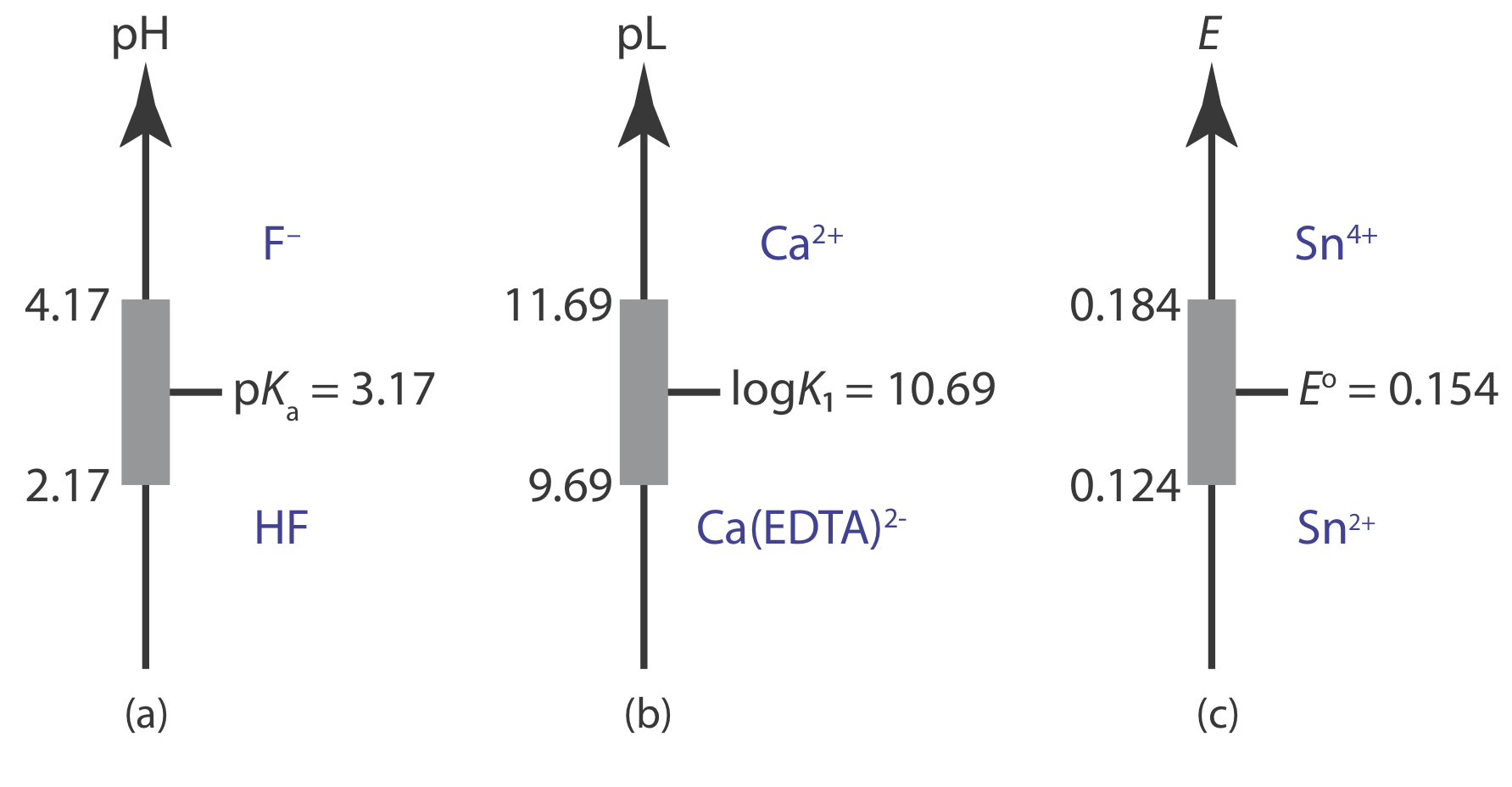
На малюнку Template:index показані діаграми сходів з буферними областями для декількох систем рівноваги.
Підготовка буфера
Буферна ємність - це здатність буфера протистояти зміні рН, коли ми додаємо в нього сильну кислоту або міцну основу. Здатність буфера протистояти зміні рН залежить від концентрацій слабкої кислоти і слабкої основи, а також їх відносних пропорцій. Важливість концентрації слабкої кислоти та концентрації слабкої основи очевидна. Чим більше родимок слабкої кислоти і слабкої основи має буфер, тим сильніше підставу або сильну кислоту він може нейтралізувати без значної зміни його рН.
Хоча більш висока концентрація буферних агентів забезпечує більшу буферну ємність, є причини використання менших концентрацій, включаючи утворення небажаних опадів і толерантність біологічних систем до високих концентрацій розчинених солей.
Відносні пропорції слабкої кислоти і слабкої основи також впливають на те, наскільки змінюється рН при додаванні сильної кислоти або міцної основи. Буфер, який є рівномолярним у слабкій кислоті та слабкій основі, вимагає більшої кількості сильної кислоти або сильної основи, щоб призвести до зміни рН на одну одиницю. Отже, буфер найбільш ефективний проти додавання сильних кислот або сильних підстав, коли його рН знаходиться поблизу значення р К слабкої кислоти.
Буферні розчини часто готують із застосуванням стандартних «рецептів», знайдених в хімічній літературі [див., наприклад, (а) Bower, V.E.; Bates, R.GJ. Res. natl. Бур. Підставка. (У. С.) 1955, 55, 197— 200; (б) Бейтс, Р.Г. Енн. Н.Ю. акад. Науковий. 1961, 92, 341—356; (c) Бейтс, Р.Г. Визначення рН, 2-е видання; Wiley-Interscience: Нью-Йорк, 1973]. Крім того, існують комп'ютерні програми та он-лайн калькулятори для допомоги у підготовці буферів [(a) Lambert, WJ J Chem. Освіта. 1990, 67, 150-153; (б) http://www.bioinformatics.org/JaMBW/5/4/index.html.]. Мабуть, найпростіший спосіб зробити буфер, однак, полягає в приготуванні розчину, який містить відповідну кон'югатную слабку кислоту і слабку основу, виміряти його рН, а потім відрегулювати рН до потрібного значення, додаючи невеликі порції або сильної кислоти, або міцної основи.
Хорошим «правилом» при виборі буфера є вибір того, реагенти якого мають p K значення, близьке до бажаного рН.
