6.6: Схеми сходів

Коли ми розробляємо або оцінюємо аналітичний метод, нам часто потрібно зрозуміти, як хімія, яка відбувається, впливає на наші результати. Припустимо, ми хочемо ізолювати Ag ⁺, осаджуючи його як AgCl. Якщо нам також потрібно контролювати рН, то треба використовувати реагент, який не робить негативного впливу на розчинність AgCl. Помилково використовувати NH ₃ для регулювання рН, наприклад, оскільки це збільшує розчинність AgCl (див. Реакцію 6.5.4). Одним з первинних джерел детермінантних помилок у багатьох аналітичних методах є неврахування потенційних хімічних перешкод.

У цьому розділі ми представимо діаграму сходів як простий графічний інструмент для візуалізації хімії рівноваги. Ми будемо використовувати сходові діаграми, щоб визначити, які реакції відбуваються при об'єднанні декількох реагентів, оцінити приблизний склад системи в рівновазі і оцінити, як зміна умов рішення може вплинути на аналітичний метод.

Хоча не спеціально на тему діаграм сходів, розроблених у цьому розділі, наступні статті надають відповідну довідкову інформацію: (а) Руно, Дж. Р.; Peters, D.G. J. Chem. Едук. 1993, 70, 708—713; (б) Вале, Дж.; Фернандес-Перейра, С.; Алькальде, М.Дж. Едук. 1993, 70, 790—795; (c) Фернандес-Перейра, К.; Вале, Дж. Педагог 1996, 6, 1—18; (d) Фернандес‐ Перейра, К.; Вале, Дж.; Алькальде, М. Педагог 2003, 8, 15—21; (е) Фернандес-Перейра, С.; Алькальде, М.; Вільєгас, Р.; Вале, Дж. Едук. 2007, 84, 520—525. Сходи діаграми є відмінним інструментом, який допоможе вам інтуїтивно мислити про аналітичну хімію. Ми будемо часто використовувати їх у наступних розділах.

Діаграми сходів для кислотно-базових рівноваг

Давайте використаємо оцтову кислоту, CH ₃ COOH, щоб проілюструвати процес, який ми будемо використовувати для малювання та інтерпретації діаграми сходів кислота-основа. Перш ніж ми намалюємо діаграму, однак, розглянемо реакцію рівноваги більш докладно. Реакція дисоціації кислоти оцтової кислоти та постійна експресія рівноваги

\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]

\[K_{\mathrm{a}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}=1.75 \times 10^{-5} \nonumber\]

Спочатку візьмемо логарифм кожного члена в цьому рівнянні і помножимо на —1

\[-\log K_{a}=4.76=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]

Тепер давайте замінимо —log [H ₃ O ⁺] на рН і переставимо рівняння, щоб отримати результат, показаний тут.

\[\mathrm{pH}=4.76+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \label{6.1}\]

Рівняння\ ref {6.1} багато говорить нам про взаємозв'язок між рН і відносними кількостями оцтової кислоти і ацетату при рівновазі. Якщо концентрації CH ₃ COOH і CH ₃ COO ^— рівні, то рівняння\ ref {6.1} знижується до

\[\mathrm{pH}=4.76+\log (1)=4.76+0=4.76 \nonumber\]

Якщо концентрація CH ₃ COO ^— більша за концентрацію CH ₃ COOH, то термін журналу в рівнянні\ ref {6.1} позитивний, а рН більше 4,76. Це розумний результат, оскільки ми очікуємо, що концентрація кон'югатної основи, CH ₃ COO ^-, збільшуватиметься у міру збільшення рН. Подібні міркування переконають вас, що рН менше 4,76, коли концентрація CH ₃ COOH перевищує концентрацію CH ₃ COO ^—.

Тепер ми готові побудувати діаграму сходів оцтової кислоти (Рисунок Template:index). Спочатку ми малюємо вертикальну стрілку, яка представляє рН розчину, з меншими (більш кислими) рівнями рН внизу і більшими (більш основними) рівнями рН вгорі. _{По-друге, проводимо горизонтальну лінію при рН, рівному величині р К оцтової кислоти.} Ця лінія, або сходинка на сходах, ділить вісь рН на регіони, де або CH ₃ COOH, або CH ₃ COO ^- переважаючий вид. На цьому схема сходів закінчена.

Рисунок Template:index. Сходова діаграма кислотно-основи для оцтової кислоти, що показує відносні концентрації CH ₃ COOH та CH ₃ COO ^—. Простіший варіант цієї діаграми сходів обходиться без рівностей та нерівностей і показує лише переважаючі види в кожному регіоні.

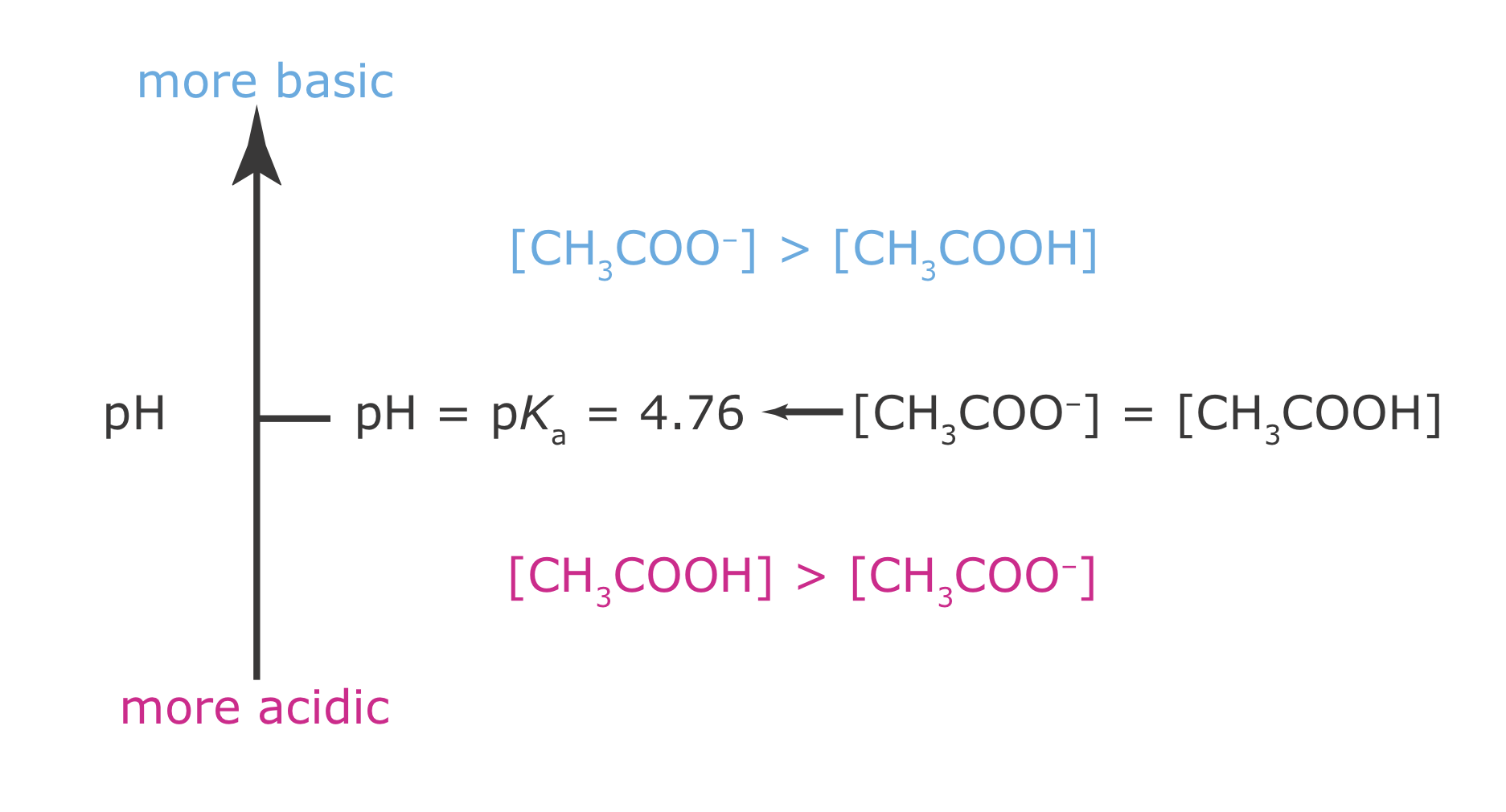
Використовуючи сходову схему, легко визначити переважну форму оцтової кислоти при будь-якому рН. При рН 3,5, наприклад, оцтова кислота існує насамперед у вигляді СН ₃ СООН. Якщо додати в розчин достатню кількість основи, щоб рН збільшився до 6,5, то переважною формою оцтової кислоти є СН ₃ СОО ^—.

Приклад Template:index

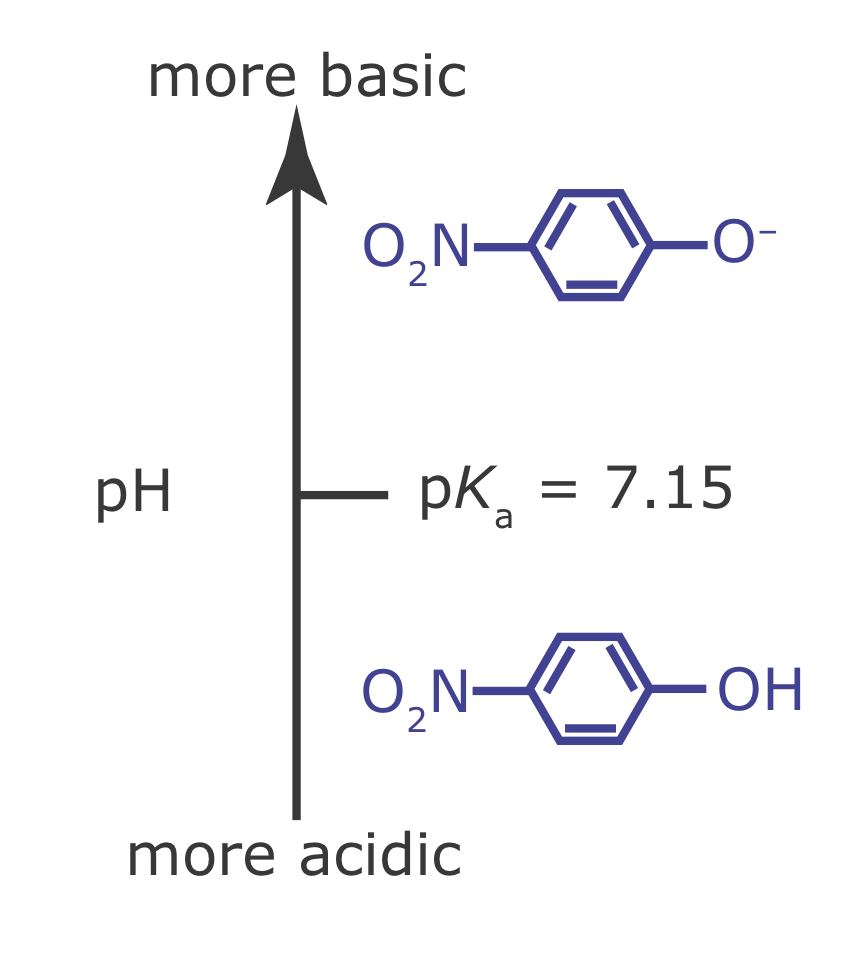
Намалюйте сходову діаграму для слабкої основи p -нітрофенолату та визначте її переважну форму при рН 6,00.

Рішення

Щоб намалювати схему сходів для слабкого підстави, просто намалюємо схему сходів для її сполученої слабкої кислоти. З додатка 11 р К _а для р -нітрофенолу становить 7,15. Отриману схему сходів показано на рисунку Template:index. При рН 6,00 р -нітрофенолат присутній переважно у слабкій кислотній формі.

Рисунок Template:index. Сходова діаграма кислотно-основи для p -нітрофенолату.

Вправа Template:index

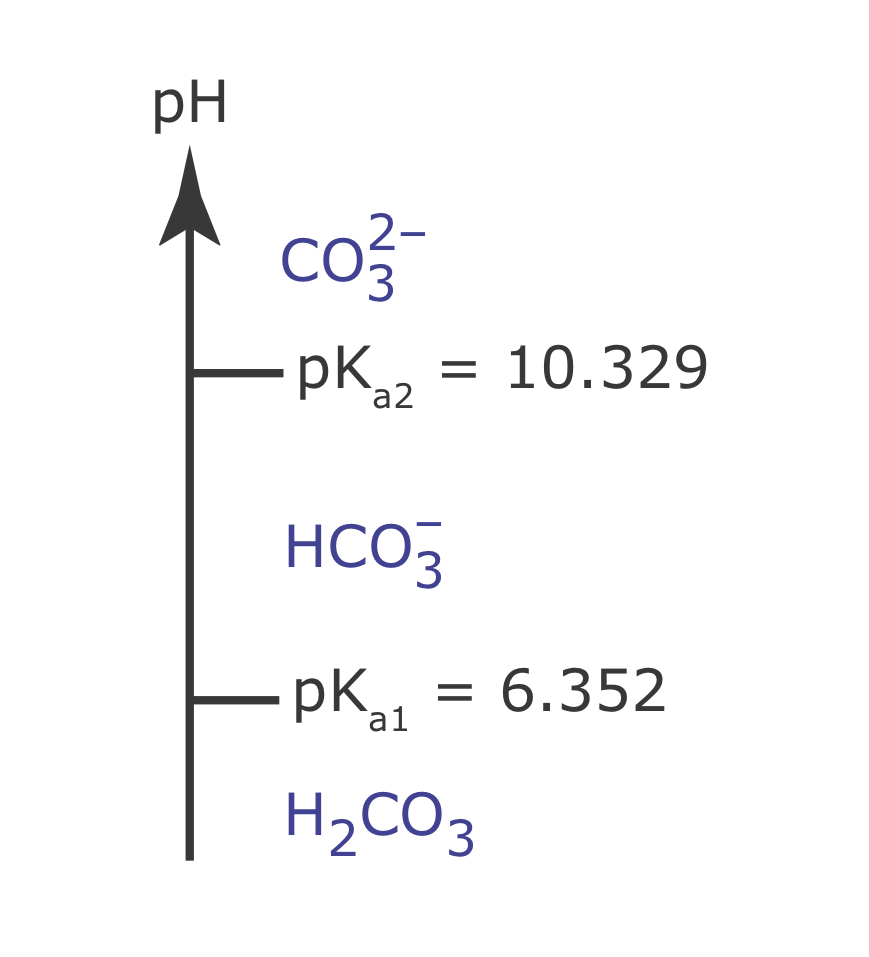
Намалюйте схему сходів для вугільної кислоти, Н ₂ СО ₃. Оскільки H ₂ CO ₃ є дипротовою слабкою кислотою, ваша діаграма сходів матиме два кроки. Яка переважна форма вугільної кислоти при рН 7,00? Відповідні константи рівноваги знаходяться в додатку 11.

Відповідь

З додатка 11 значення р К _а для Н ₂ СО _{3 становлять} 6,352 і 10,329. Схема сходів для Н ₂ СО ₃ показана нижче. Переважною формою при рН 7,00 є\(\text{HCO}_3^-\).

Діаграма сходів особливо корисна для оцінки реактивності між слабкою кислотою та слабкою основою. Наприклад, на малюнку Template:index} показана єдина сходова діаграма для оцтової кислоти/ацетату та p -нітрофенола/ p -нітрофенолату. Кислота та основа не можуть співіснувати, якщо їх відповідні області переважання не перекриваються. Якщо змішати разом розчини оцтової кислоти і р -нітрофенолату натрію, то реакція

\[\mathrm{C}_{6} \mathrm{H}_{4} \mathrm{NO}_{2}^{-}(a q)+\mathrm{CH}_{3} \mathrm{COOH}(a q)\rightleftharpoons \text{CH}_3\text{COO}^-(aq) + \text{C}_6\text{H}_4\text{NO}_2\text{H}(aq) \label{6.2}\]

відбувається тому, що ділянки переважання оцтової кислоти і р -нітрофенолату не перекриваються. Кінцевий склад розчину залежить від того, який вид є граничним реагентом. Наступний приклад показує, як ми можемо використовувати діаграму сходів на малюнку Template:index для оцінки результату змішування разом розчинів оцтової кислоти та p -нітрофенолату.

Рисунок Template:index. Сходова діаграма кислотно-основи, що показує області переважання оцтової кислоти/ацетату та p -нітрофенола/р -нітрофенолату. Області, затінені синім кольором, показують діапазон рН, де слабкі основи є переважаючими видами; слабкі кислотні форми є переважаючими видами в районах, затінених рожевим кольором.

Приклад Template:index

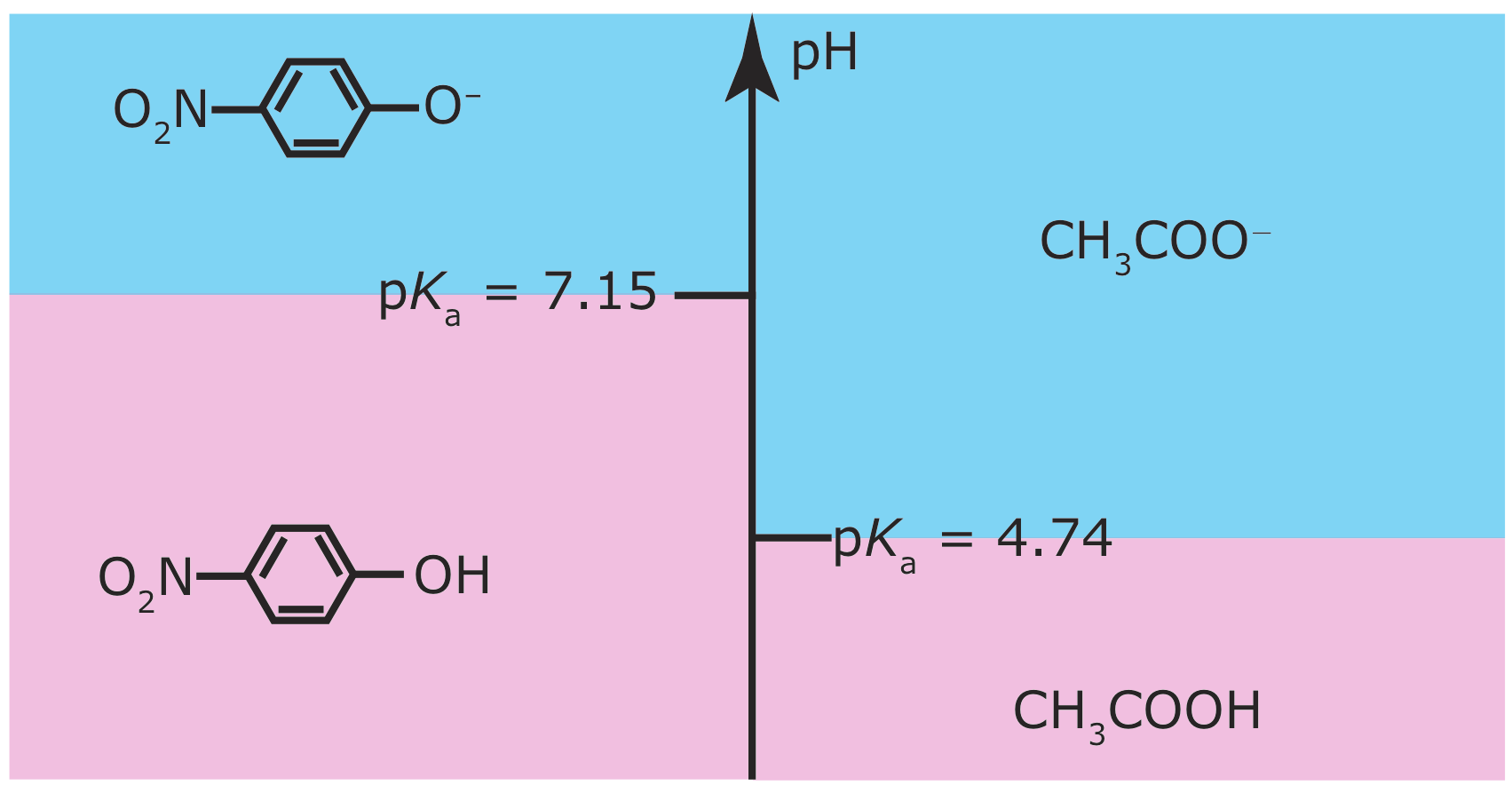
Прогнозують приблизний рН і кінцевий склад після змішування між собою 0,090 моль оцтової кислоти і 0,040 моль р -нітрофенолату.

Рішення

Діаграма сходів на малюнку Template:index вказує на те, що реакція між оцтовою кислотою та p -нітрофенолатом є сприятливою. Оскільки оцтова кислота в надлишку, ми припускаємо, що реакція р -нітрофенолату на р -нітрофенол завершена. При рівновазі по суті не залишається p -нітрофенолату і є 0,040 моль р -нітрофенолу. Перетворення р -нітрофенолату в р -нітрофенол споживає 0,040 моль оцтової кислоти; таким чином

\[\begin{array}{c}{\text { moles } \mathrm{CH}_{3} \mathrm{COOH}=0.090-0.040=0.050 \ \mathrm{mol}} \\ {\text { moles } \mathrm{CH}_{3} \mathrm{COO}^{-}=0.040 \ \mathrm{mol}}\end{array} \nonumber\]

За сходовою діаграмою рН дорівнює 4,74 при рівних кількостях СН ₃ СООН і СН ₃ СОО ^—. Оскільки у нас є трохи більше CH ₃ COOH, ніж CH ₃ COO ^-, рН трохи менше 4,74.

Вправа Template:index

Використовуючи рис. Template:index, прогнозують приблизний рН і склад розчину, утвореного змішуванням між собою 0,090 молів р -нітрофенолату і 0,040 моль оцтової кислоти.

Відповідь

Діаграма сходів на малюнку Template:index вказує на те, що реакція між оцтовою кислотою та p -нітрофенолатом є сприятливою. Оскільки р -нітрофенолат знаходиться в надлишку, ми припускаємо, що реакція оцтової кислоти на ацетат завершена. При рівновазі по суті не залишається оцтової кислоти і є 0,040 моль ацетату. Перетворення оцтової кислоти в ацетат споживає 0,040 моль р -нітрофенолату; таким чином

\[\text { moles } p \text {-nitrophenolate }=0.090-0.040=0.050 \text { mol } \nonumber\]

\[\text { moles } p\text{-nitrophenol }=0.040 \ \mathrm{mol} \nonumber\]

Згідно зі сходовою діаграмою для цієї системи, рН становить 7,15, коли є рівні концентрації р -нітрофенолу та p -нітрофенолату. Оскільки у нас трохи більше р -нітрофенолату, ніж у нас p -нітрофенолу, рН трохи більше, ніж 7,15.

Якщо ділянки переважання для кислоти і основи перекриваються, то ми не очікуємо, що відбудеться велика частина реакції. Наприклад, якщо змішати разом розчини CH ₃ COO ^- і p -нітрофенолу, ми не очікуємо значної зміни молів будь-якого реагенту. Крім того, рН суміші повинен бути між 4,76 і 7,15, причому точний рН залежить від відносних кількостей CH ₃ COO ^- і p -нітрофенолу.

Ми також можемо використовувати діаграму кислотно-основи для оцінки впливу рН на інші рівноваги. Наприклад, розчинність CaF ₂

\[\mathrm{CaF}_{2}(s) \rightleftharpoons \mathrm{Ca}^{2+}(a q)+2 \mathrm{F}^{-}(a q) \nonumber\]

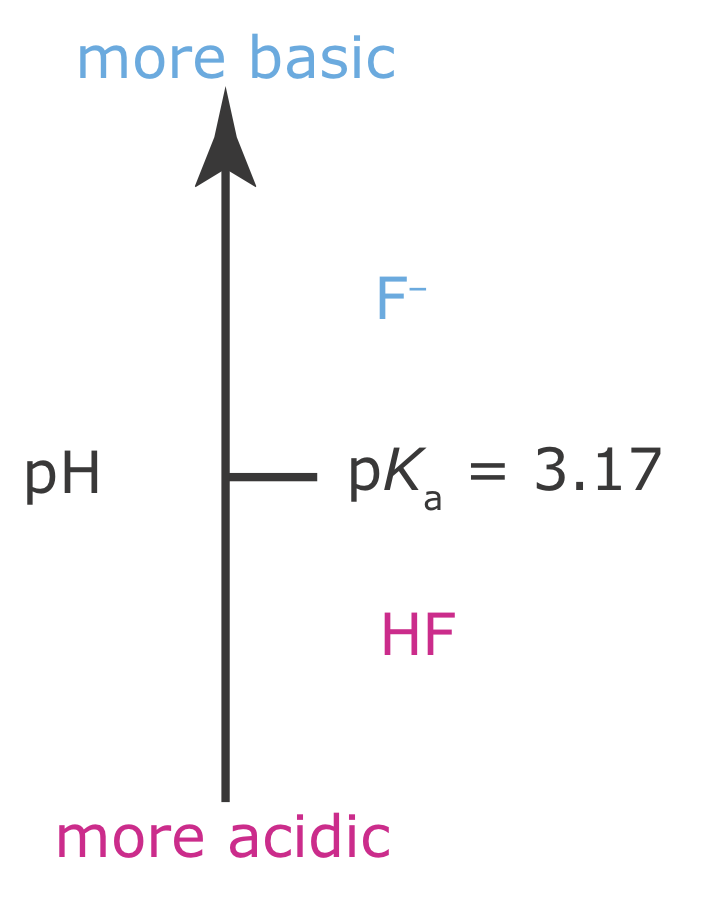
впливає на рН, оскільки F ^— це слабка основа. З принципу Le ChaTelier ми знаємо, що перетворення F ^- в HF збільшить розчинність CaF ₂. Щоб мінімізувати розчинність CaF ₂, нам потрібно підтримувати рН розчину, щоб F ^— це переважаючий вид. Діаграма сходів для ВЧ (рис. Template:index) показує нам, що підтримка рН більше 3,17 мінімізує втрати розчинності.

Рисунок Template:index. Кислотно-базова сходи діаграма для ВЧ. Щоб мінімізувати розчинність CaF ₂, нам потрібно підтримувати рН вище 3,17, причому більш базові рівні рН призводять до менших втрат розчинності. Див. Розділ 8 для більш детального обговорення.

Діаграми сходів для рівноваги комплексоутворення

Ми можемо застосувати ті ж принципи для побудови та інтерпретації діаграми кислотно-основи сходів до рівноваг, які включають комплекси метал-ліганд. Для реакції комплексоутворення ми визначаємо шкалу сходової діаграми, використовуючи концентрацію некомплексованого, або вільного ліганду, pL. Використовуючи формування в\(\text{Cd(NH}_3)^{2+}\) якості прикладу

\[\mathrm{Cd}^{2+}(a q)+\mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}(a q) \nonumber\]

ми можемо показати, що журнал K ₁ є розділовою лінією між областями переважання для Cd ^{2 +} і for\(\text{Cd(NH}_3)^{2+}\).

\[K_{1}=3.55 \times 10^{2}=\frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]\left[\mathrm{NH}_{3}\right]} \nonumber\]

\[\log K_{1}=\log \left(3.55 \times 10^{2}\right)=\log \frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]}-\log \left[\mathrm{NH}_{3}\right] \nonumber\]

\[\log K_{1}=2.55=\log \frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]}+\mathrm{p} \mathrm{NH}_{3} \nonumber\]

\[\mathrm{p} \mathrm{NH}_{3}=\log K_{1}+\log \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}=2.55+\log \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]} \nonumber\]

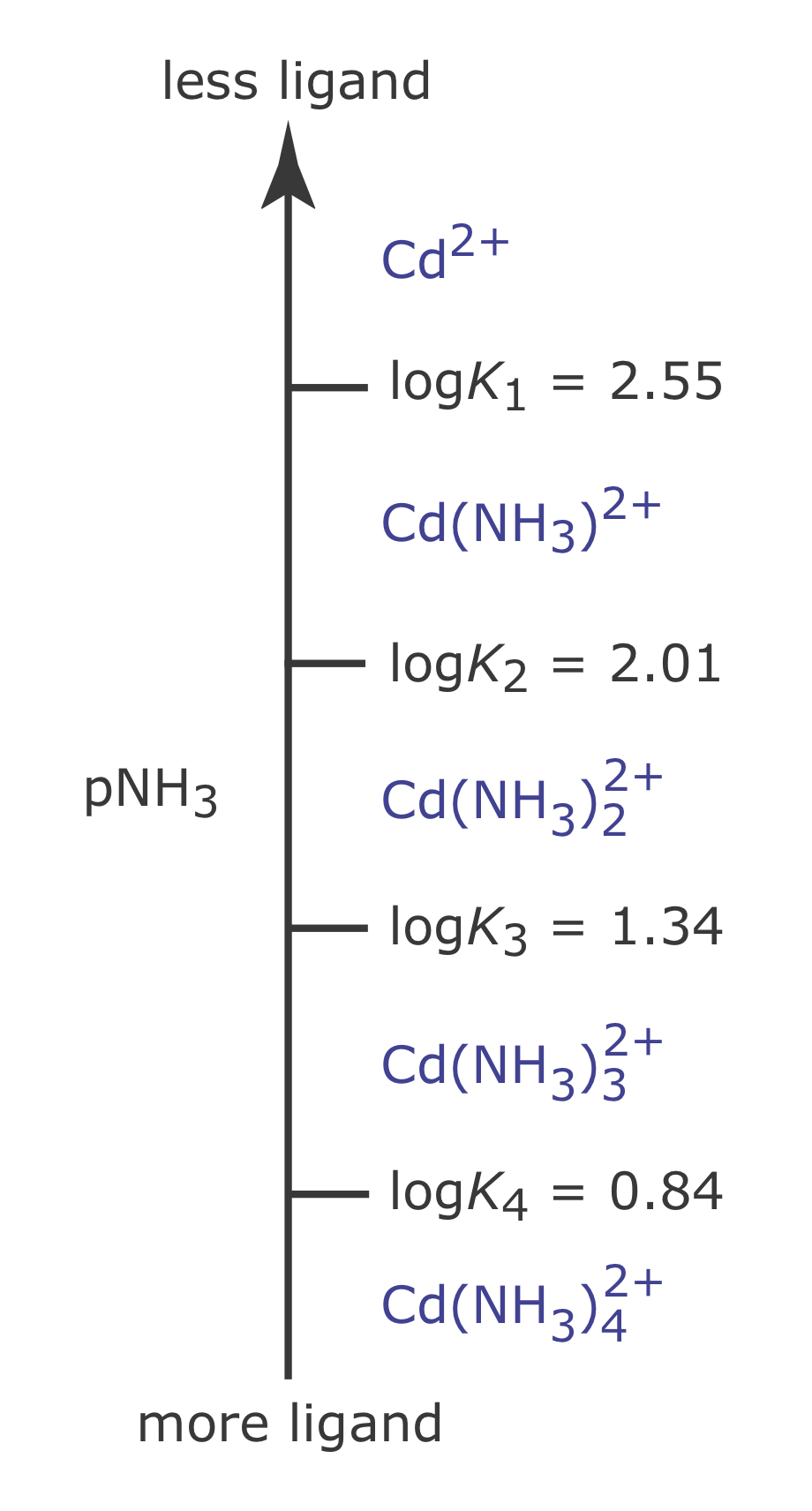
Таким чином, Cd ^{2 +} є переважаючим видом, коли PnH ₃ перевищує 2,55 (концентрація NH ₃ менша за\(2.82 \times 10^{-3}\) M), а для значення PnH ₃ менше 2,55\(\text{Cd(NH}_3)^{2+}\) є переважаючим видом. На малюнку Template:index показана повна діаграма сходів метал-ліганд для Cd ^{2 +} та NH ₃, яка включає додаткові комплекси Cd—nH ₃.

Рисунок Template:index. Діаграма сходів метал-ліганд для реакцій комплексоутворення Cd ^{2 +} —NH ₃. Зверніть увагу, що комплекси вищого порядку утворюються, коли pNH ₃ менше (що відповідає більшим концентраціям NH ₃).

Приклад Template:index

Намалюйте єдину схему сходів для комплексів Ca (EDTA) ^2- та Mg (EDTA) ^2— метал-ліганд. Використовуйте діаграму сходів, щоб передбачити результат додавання 0,080 молів Са ^{2 +} до 0,060 молів Mg (EDTA) ^2—. ЕДТА - це абревіатура ліганду етилендіамінтетраоцтової кислоти.

Рішення

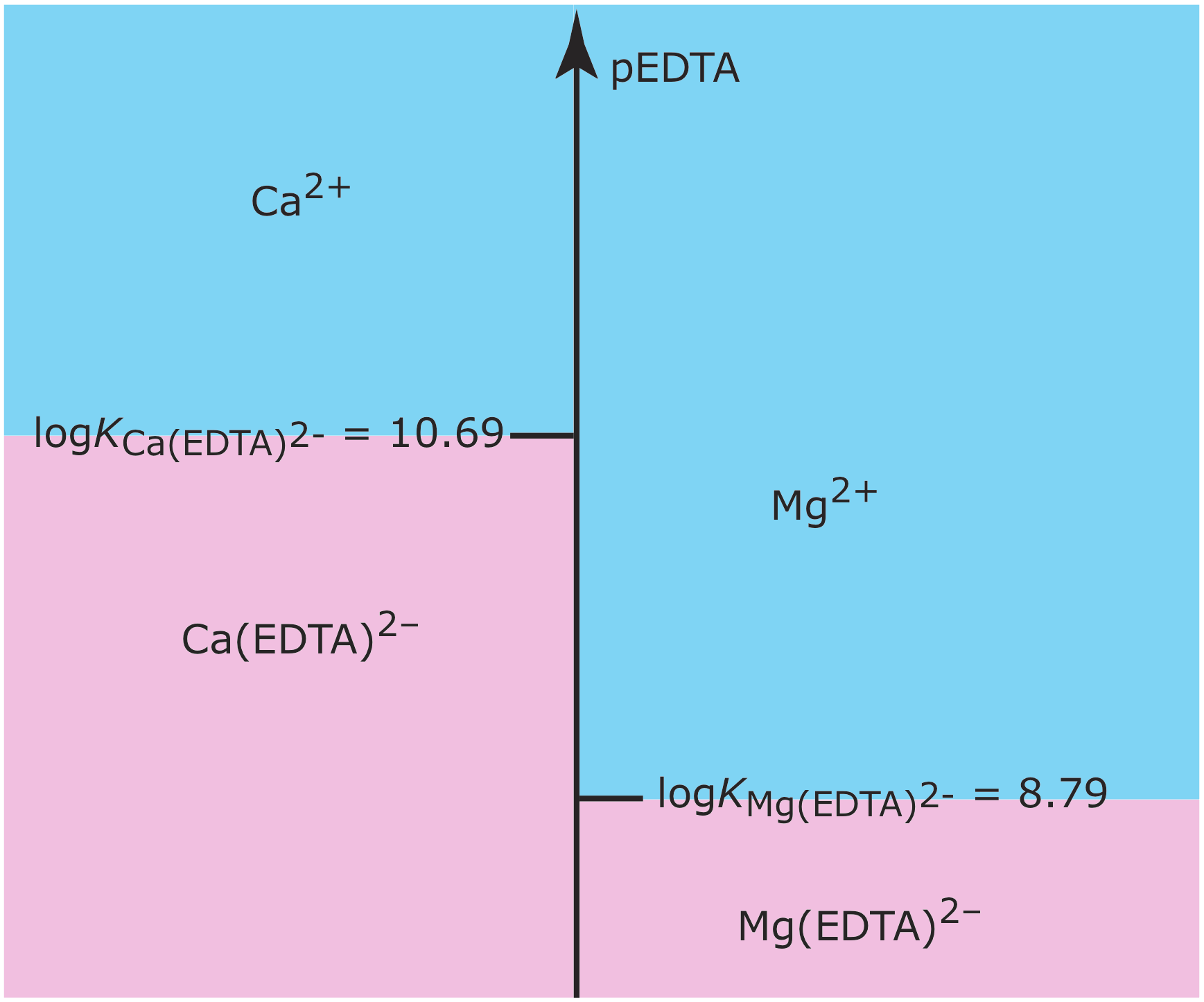
На малюнку Template:index показана схема сходів для цієї системи комплексів метал—ліганд. Оскільки області переважання для Ca ^{2 +} і Mg (ЕДТА) ^2‐ не перекриваються, реакція

\[\mathrm{Ca}^{2+}(a q)+\mathrm{Mg}(\mathrm{EDTA})^{2-}(a q) \rightleftharpoons \mathrm{Ca}(\mathrm{EDTA})^{2-}(a q)+\mathrm{Mg}^{2+}(a q) \nonumber\]

доходить по суті до доопрацювання. Оскільки Са ^{2 +} є надлишком реагенту, склад кінцевого розчину приблизно

\[\text { moles } \mathrm{Ca}^{2+}=0.080-0.060=0.020 \ \mathrm{mol} \nonumber\]

\[\text { moles } \mathrm{Ca}(\mathrm{EDTA})^{2-}=0.060 \ \mathrm{mol} \nonumber\]

\[\text { moles } \mathrm{Mg}^{2+}=0.060 \ \mathrm{mol} \nonumber\]

\[\text { moles } \mathrm{Mg}(\mathrm{EDTA})^{2-}=0 \ \mathrm{mol} \nonumber\]

Рисунок Template:index. Металево-лігандна сходи діаграма для Са (ЕДТА) ^2— і для Mg (EDTA) ^2—. Області, затінені синім кольором, показують діапазон PedTA, де переважаючими видами є іони вільних металів; комплекси метал-ліганд є переважаючими видами в районах, затінених рожевим кольором.

Діаграма сходів метал-ліганд на рисунку Template:index використовує константи ступеневого формування. Ми також можемо побудувати схему сходів, використовуючи кумулятивні константи формування. Наприклад, перші три ступінчасті константи формування для реакції Zn ^{2 +} з NH ₃

\[\mathrm{Zn}^{2+}(a q)+\mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Zn}\left(\mathrm{NH}_{3}\right)^{2+}(a q) \quad K_{1}=1.6 \times 10^{2} \nonumber\]

\[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)^{2+}(a q)+\mathrm{NH}_{3}(a q)\rightleftharpoons\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q) \quad K_{2}=1.95 \times 10^{2} \nonumber\]

\[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q)+\mathrm{NH}_{3}(a q)=\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q) \quad K_{3}=2.3 \times 10^{2} \nonumber\]

говорить про те, що формування\(\text{Zn(NH}_3)_3^{2+}\) є більш сприятливим, ніж утворення\(\text{Zn(NH}_3)^{2+}\) або\(\text{Zn(NH}_3)_2^{2+}\). З цієї причини рівновага найкраще представлена реакцією кумулятивного формування, показаної тут.

\[\mathrm{Zn}^{2+}(a q)+3 \mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q) \quad \beta_{3}=7.2 \times 10^{6} \nonumber\]

Оскільки К ₃ більше, ніж К ₂, що більше, ніж К ₁, утворення металолігандного комплексу\(\text{Zn(NH}_3)_3^{2+}\) є більш сприятливим, ніж формування інших комплексів металевих лігандів. З цієї причини при більш низьких значеннях PnH ₃\(\text{Zn(NH}_3)_3^{2+}\) концентрація більше концентрації\(\text{Zn(NH}_3)^{2+}\) або\(\text{Zn(NH}_3)_2^{2+}\). Значення\(\beta_3\) є

\[\beta_{3}=K_{1} \times K_{2} \times K_{3} \nonumber\]

Щоб побачити, як ми включаємо цю сукупну константу формування в діаграму сходів, ми починаємо з вираження постійної рівноваги реакції.

\[\beta_{3}=\frac{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]}{\left[\mathrm{Zn}^{2+}\right]\left[\mathrm{NH}_{3}\right]^{3}} \nonumber\]

Взяття колоди з кожного боку

\[\log \beta_{3}=\log \frac{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]}{\left[\mathrm{Zn}^{2+}\right]}-3 \log \left[\mathrm{NH}_{3}\right] \nonumber\]

і перестановка дає

\[\mathrm{pNH}_{3}=\frac{1}{3} \log \beta_{3}+\frac{1}{3} \log \frac{\left[\mathrm{Zn}^{2+}\right]}{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]} \nonumber\]

Коли концентрації Zn і\(\text{Zn(NH}_3)_3^{2+}\) рівні, то

\[\mathrm{p} \mathrm{NH}_{3}=\frac{1}{3} \log \beta_{3}=2.29 \nonumber\]

Загалом для комплексу метал—ліганд ML _n кроком для константи кумулятивного формування є

\[\mathrm{pL}=\frac{1}{n} \log \beta_{n} \nonumber\]

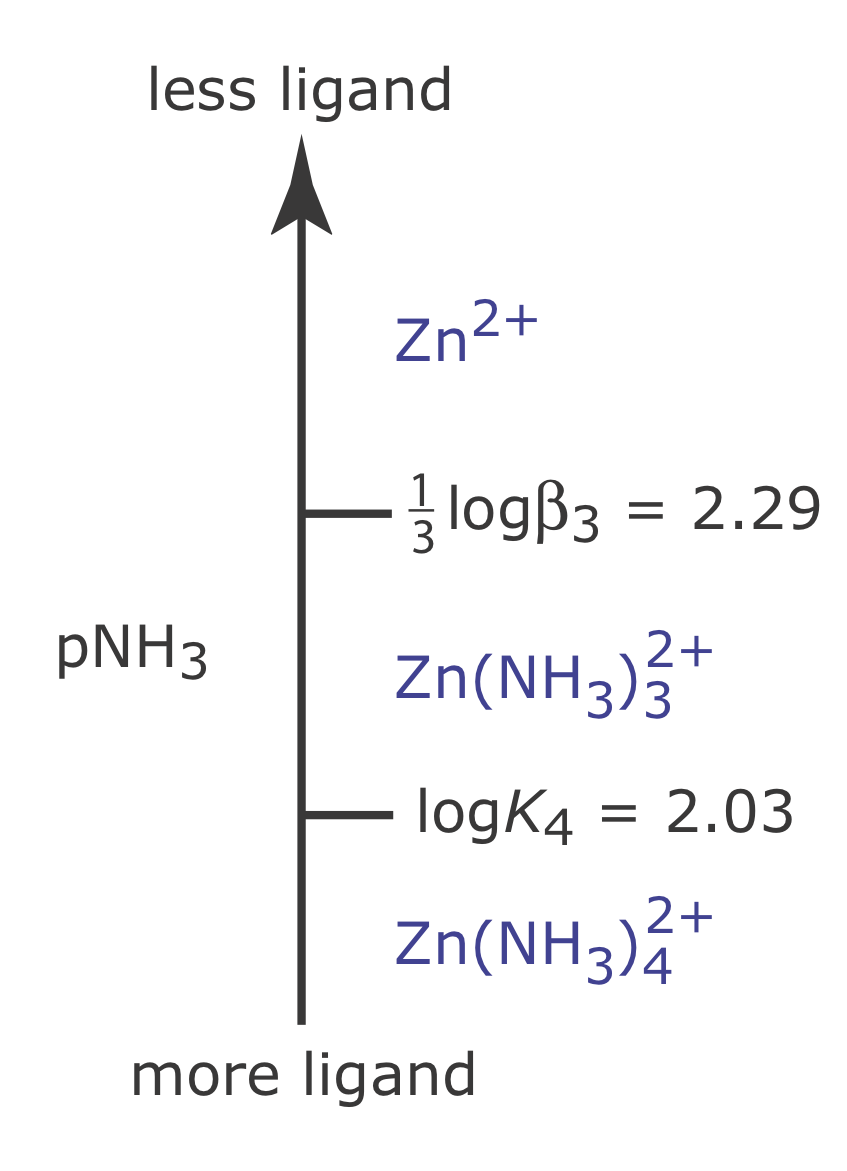
На малюнку Template:index показана повна схема сходів для системи Zn ^{2 +} —NH ₃.

Рисунок Template:index. Діаграма сходів для реакцій комплексоутворення метал-ліганд Zn ^{2 +} —NH ₃, що показує як крок, заснований на константі кумулятивного формування, так і крок, заснований на константі ступеневого формування.

Діаграми сходів для окислення/зменшення рівноваг

Ми також можемо побудувати діаграми сходів, щоб допомогти нам оцінити окислювально-відновні рівноваги. Рисунок Template:index показує типову діаграму сходів для двох напівреакцій, в яких масштаб є потенціалом, E.

Рисунок Template:index. ^{Діаграма окислювально-відновних сходів для Fe 3 +/Fe 2+ і для Sn 4+/Sn 2+.} Ділянки, затінені синім кольором, показують потенційний діапазон, де окислені форми є переважаючими видами; зменшені форми є переважаючими видами на ділянках, затінених рожевим кольором. Відзначимо, що більш позитивний потенціал сприяє окисленій формі.

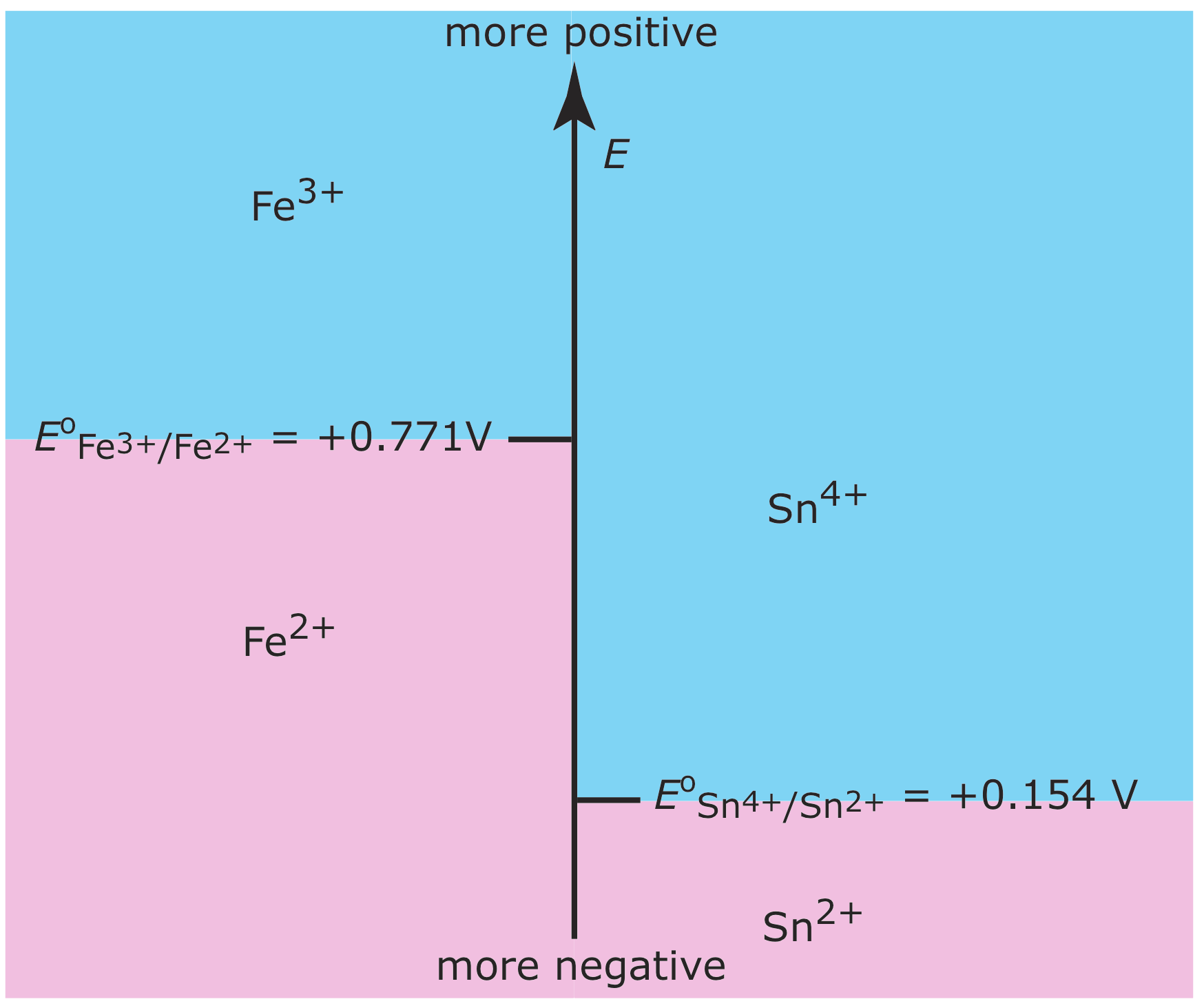
Рівняння Нернста визначає області переважання. Використовуючи в якості прикладу реакцію Fe ^{3 + /Fe 2 +}, пишемо

\[E=E^{\circ}-\frac{R T}{n F} \ln \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]}=0.771-0.05916 \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]} \nonumber\]

При потенціалі більш позитивному, ніж стандартний державний потенціал, переважаючим видом є Fe ^{3 +}, тоді як Fe ^{2 +} переважає при потенціалах більш негативних, ніж E ^o. У поєднанні з кроком для напівреакції Sn ^{4 +/Sn 2+} ми бачимо, що Sn ^{2 +} є корисним відновником для Fe ^{3 +}. Якщо Sn ^{2 +} знаходиться в надлишку, потенціал отриманого розчину близько +0,154 В.

Оскільки кроки на діаграмі окислювально-відновних сходів є стандартними потенціалами стану, виникає ускладнення, якщо розчинні речовини, відмінні від окислювача та відновника, присутні при нестандартних концентраціях стану. Наприклад, потенціал для напівреакції

\[\mathrm{UO}_{2}^{2+}(a q)+4 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+2 e^{-} \rightleftharpoons \mathrm{U}^{4+}(a q)+6 \mathrm{H}_{2} \mathrm{O}(l) \nonumber\]

залежить від рН розчину. Для визначення областей переважання в цьому випадку ми починаємо з рівняння Нернста.

\[E=+0.327-\frac{0.05916}{2} \log \frac{\left[\mathrm{U}^{4+}\right]}{\left[\mathrm{UO}_{2}^{2+}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}} \nonumber\]

і коефіцієнт концентрації Н ₃ О ⁺.

\[E=+0.327+\frac{0.05916}{2} \log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}-\frac{0.05916}{2} \log \frac{\left[\mathrm{U}^{4+}\right]}{\left[\mathrm{UO}_{2}^{2+}\right]}\nonumber\]

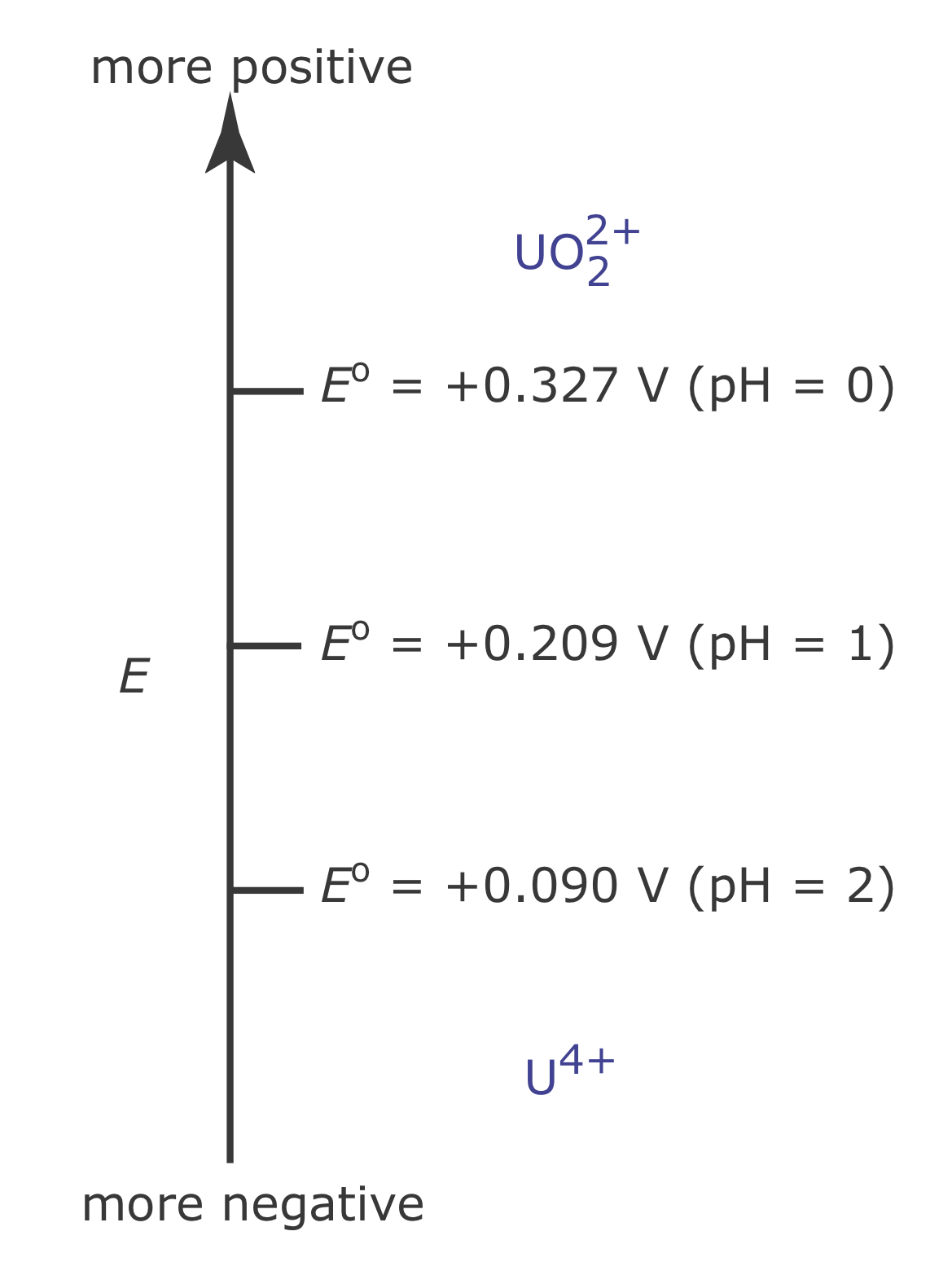
З цього рівняння ми бачимо, що площа переважання для\(\text{UO}_2^{2+}\) і U ⁴⁺ визначається кроком при потенціалі, де [U ⁴⁺] = [\(\text{UO}_2^{2+}\)].

\[E=+0.327+\frac{0.05916}{2} \log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}=+0.327-0.1183 \mathrm{pH} \nonumber\]

Рисунок Template:index показує, як рН впливає на крок для\(\text{UO}_2^{2+}\) /U ⁴⁺ напів-реакції.

Рисунок Template:index. Діаграма окислювально-відновлювальної сходи для\(\text{UO}_2^{2+}\) напівреакції/U ⁴⁺, що показує вплив рН на крок, який визначається потенціалом стандартного стану.