6.9: Ефекти активності
- Page ID
- 24921
Ретельні вимірювання на комплексі метал—ліганд Fe (SCN) 2+ свідчать про зниження його стабільності в присутності інертних іонів [Lister, MW; Rivington, D.E. Can. Дж. Хем. 1995, 33, 1572—1590]. Ми можемо продемонструвати це, додаючи інертну сіль до рівноважної суміші Fe 3 + та SCN —. Рисунок Template:index a показує результат змішування між собою рівних об'ємів 1,0 мм FeCl 3 і 1,5 мм KSCN, обидва з яких безбарвні. Червонувато-помаранчевий колір розчину обумовлений утворенням Fe (SCN) 2+.

Додавання 10 г KNO 3 до розчину і перемішування для розчинення твердої речовини дає результат, показаний на рисунку Template:index b. Більш світлий колір розчину говорить про те, що додавання KNO 3 зміщує реакцію\ ref {6.1} вліво, зменшуючи концентрацію Fe (SCN) 2+ та підвищення концентрації Fe 3 + та SCN —. Результатом є зменшення константи формування комплексу, К 1.
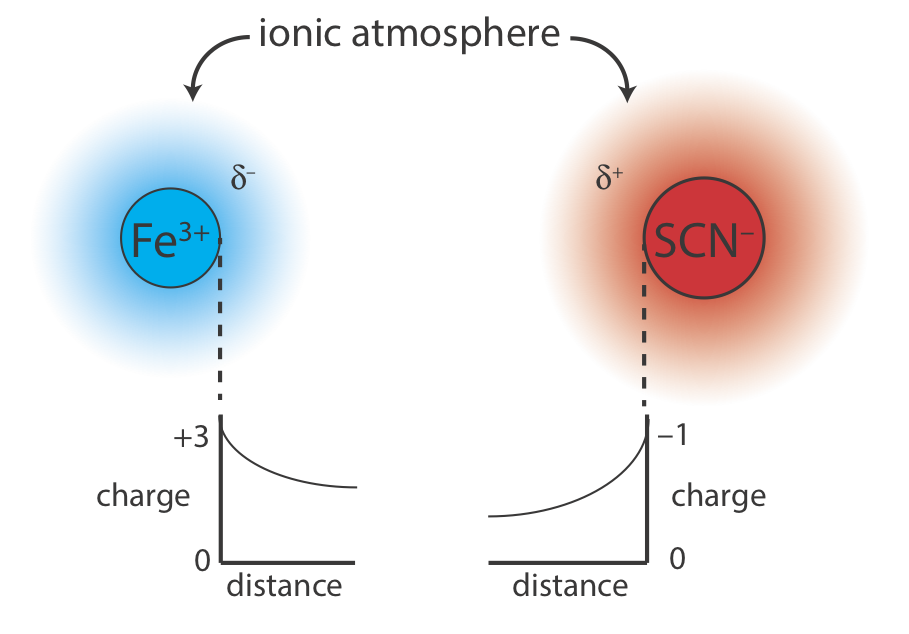
Чому додавання інертного електроліту має впливати на положення рівноваги реакції? Пояснити вплив КНО 3 на утворення Fe (SCN) 2+ можна, якщо розглядати реакцію в мікроскопічному масштабі. Розв'язок на рисунку Template:index b містить різноманітні катіони та аніони: Fe 3 +, SCN —, K +\(\text{NO}_3^-\), H 3 O + та OH —. Хоча розчин однорідний, в середньому аніонів у регіонах поблизу іонів Fe 3 + трохи більше, а катіонів у регіонах поблизу SCN — іонів трохи більше. Як показано на малюнку Template:index, кожен іон Fe 3 + і кожен SCN — іон оточений іонною атмосферою протилежного заряду (\(\delta^–\)і\(\delta^+\)), яка частково екранує іони один від одного. Оскільки очевидний заряд кожного іона на краю його іонної атмосфери менше, ніж його фактичний заряд, сила тяжіння між двома іонами менша. В результаті утворення Fe (SCN) 2+ є дещо менш сприятливим, а константа формування в Equation\ ref {6.2} дещо менша. Більш високі концентрації КНО 3 збільшуються\(\delta^–\) і\(\delta^+\), в результаті чого з'являються ще менші значення для константи формування.
Іонна сила
Щоб зарахувати концентрацію іонів у константу утворення для Fe (SCN) 2+, нам потрібен спосіб виразити цю концентрацію значущим чином. Оскільки як концентрація іона, так і його заряд є важливими, ми визначаємо іонну силу розчину,\(\mu\) як
\[\mu=\frac{1}{2} \sum_{i=1}^{n} c_{i} z_{i}^{2} \nonumber\]
де c i і z i - концентрація і заряд їх i іона.
Розрахуйте іонну міцність розчину 0,10 М NaCl. Повторіть розрахунок для розчину 0,10 М Na 2 SO 4.
Рішення
Іонна сила для 0,10 М NaCl становить
\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{Cl}^{-}\right] \times(-1)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.10) \times(+1)^{2}+(0.10) \times(-1)^{2}\right\}=0.10 \ \mathrm{M}}\end{array} \nonumber\]
Для 0,10 М Na 2 SO 4 іонна сила дорівнює
\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{SO}_{4}^{2-}\right] \times(-2)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.20) \times(+1)^{2}+(0.10) \times(-2)^{2}\right\}=0.30 \ \mathrm{M}}\end{array} \nonumber\]
При розрахунку іонних сильних сторін цих розчинів ми ігноруємо наявність H 3 O + і OH —, і, у випадку Na 2 SO 4, наявність\(\text{HSO}_4^-\) від основи реакції дисоціації\(\text{SO}_4^{2-}\). У разі 0,10 М NaCl концентрації H 3 O + та OH — є\(1.0 \times 10^{-7}\), що значно менше концентрацій Na + та Cl —. Оскільки\(\text{SO}_4^{2-}\) це дуже слабка основа (K b =\(1.0 \times 10^{-12}\)), розчин лише трохи основний (рН = 7,5), а концентрації Н 3 О +, ОН — і\(\text{HSO}_4^-\) незначні. Хоча ми можемо ігнорувати наявність H 3 O +, OH -, і\(\text{HSO}_4^-\) коли ми обчислюємо іонну силу цих двох розчинів, пам'ятайте, що реакція рівноваги може генерувати іони, які можуть вплинути на іонну силу розчину.
Зверніть увагу, що одиницею іонної сили є молярність, але іонна сила солі не повинна відповідати її молярної концентрації. Для солі 1:1, наприклад NaCl, іонна сила і молярна концентрація ідентичні. Іонна сила електроліту 2:1, такого як Na 2 SO 4, втричі перевищує молярну концентрацію електроліту.
Коефіцієнти активності та активності
Рисунок Template:index показує, що додавання KNO 3 до суміші Fe 3 + та SCN — зменшує константу формування для Fe (SCN) 2+. Це створює протиріччя. Раніше в цьому розділі ми показали, що існує взаємозв'язок між вільною енергією стандартного стану реакції, G o, і її константою рівноваги, K.
\[\triangle G^{\circ}=-R T \ln K \nonumber\]
Оскільки реакція має лише один стандартний стан, її константа рівноваги повинна бути незалежною від умов розв'язання. Хоча іонна сила впливає на явну константу формування для Fe (SCN) 2+, реакція\ ref {6.1} повинна мати основну термодинамічну константу формування, яка не залежить від іонної сили.
Видима константа формування для Fe (SCN) 2+, як показано в Equation\ ref {6.2}, є функцією концентрацій. Замість концентрацій ми визначаємо справжню термодинамічну постійну рівноваги за допомогою діяльності. Активність виду A, A, є добутком його концентрації, [A] та коефіцієнта активності, залежного від розв'язку,\(\gamma_A\)
\[a_{A}=[A] \gamma_{A} \nonumber\]
Справжня термодинамічна константа формування для Fe (SCN) 2+, отже, є
\[K_{1}=\frac{a_{\mathrm{Fe}(S \mathrm{CN})^{2+}}}{a_{\mathrm{Fe}^{3+}} \times a_{\mathrm{SCN}^-}}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}\right] \gamma_{\mathrm{Fe}(\mathrm{SCN})^{2+}}}{\left[\mathrm{Fe}^{3+}\right] \gamma_{\mathrm{Fe}^{3+}}\left[\mathrm{SCN}^{-}\right] \gamma_{\mathrm{SCN}^{-}}} \nonumber\]
Якщо не вказано інше, константи рівноваги в додатках є термодинамічними константами рівноваги.
Коефіцієнт активності виду коригує будь-яке відхилення між його фізичною концентрацією та ідеальним значенням. Для газу, чистої твердої речовини, чистої рідини або неіонного розчиненого речовини коефіцієнт активності становить приблизно один при найбільш розумних експериментальних умовах.
Для газу належними умовами є коефіцієнт неміцності та неміцності, а не коефіцієнт активності та активності.
Для реакції, яка включає лише ці види, різниця між активністю та концентрацією незначна. Коефіцієнт активності іона, однак, залежить від іонної сили розчину, заряду іона та розміру іона. Оцінити коефіцієнти активності можна за допомогою розширеного рівняння Дебає-Гюкеля
де z A - заряд іона,\(\alpha_A\) ефективний діаметр гідратованого іона в нанометрах (табл. 6.2),\(\mu\) іонна сила розчину, а 0,51 і 3.3 - константи, придатні для водного розчину при 25 o С. Ефективний радіус іона - це радіус іона плюс ті молекули води, тісно пов'язані з іоном. Ефективний радіус більший для менших, більш сильно заряджених іонів, ніж для більших, менш сильно заряджених іонів.
| іон | ефективний діаметр (нм) |
|---|---|
|
Н 3 О + |
0.9 |
|
Лі + |
0.6 |
|
Na +\(\text{IO}_3^-\),\(\text{HSO}_3^-\),\(\text{HCO}_3^-\),\(\text{H}_2\text{PO}_4^-\) |
0,45 |
|
О —, Ф —, СКН —, ГС —\(\text{ClO}_3^-\),\(\text{ClO}_4^-\),\(\text{MnO}_4^-\) |
0,35 |
|
K +, Cl —, Br —, I —, CN —\(\text{NO}_2^-\),\(\text{NO}_3^-\) |
0.3 |
|
Сс +, Тл +, Аг +,\(\text{NH}_4^+\) |
0,25 |
|
Мг 2 +, Be 2+ |
0.8 |
|
Са 2 +, Су 2+, Зн 2 +, Сн 2+, Мн 2 +, Фе 2+, Ні 2 +, Со 2+ |
0.6 |
|
Ср 2 +, Ба 2+, Кд 2+, Хг 2+, S 2— |
0,5 |
|
Пб 2+,\(\text{SO}_4^{2-}\),\(\text{SO}_3^{2-}\) |
0,45 |
|
\(\text{Hg}_2^{2+}\),\(\text{SO}_4^{2-}\),\(\text{S}_22\text{O}_3^{2-}\),\(\text{CrO}_4^{2-}\),\(\text{HPO}_4^{2-}\) |
0,40 |
|
Всі 3 +, лют 3+, Кр 3 + |
0.9 |
|
\(\text{PO}_4^{3-}\),\(\text{Fe(CN)}_6^{3-}\) |
0.4 |
|
Зр 4 +, Се 4+, Сн 4 + |
1.1 |
|
\(\text{Fe(CN)}_6^{4-}\) |
0,5 |
|
Джерело: Kielland, Дж. Хім. Соц. 1937, 59, 1675—1678. |
Кілька особливостей Equation\ ref {6.3} заслуговують на нашу увагу. По-перше, коли іонна сила наближається до нуля, коефіцієнт активності іона наближається до значення одиниці. У розчині\(\mu = 0\), де активність іона та його концентрація ідентичні. Ми можемо скористатися цим фактом, щоб визначити постійну термодинамічної рівноваги реакції шляхом вимірювання видимої постійної рівноваги для декількох все менших іонних сильних сторін і екстраполяції назад до іонної сили нуля. По-друге, коефіцієнт активності менше, а ефект активності важливіший, для іона з більш високим зарядом і меншим ефективним радіусом. Нарешті, розширене рівняння Дебіє-Гюкеля забезпечує розумну оцінку коефіцієнта активності іона, коли іонна сила менше 0,1. Модифікації рівняння\ ref {6.3} розширюють розрахунок коефіцієнтів активності до більш високих іонних сильних сторін [Davies, C. W. Ion Association, Баттерворт: Лондон, 1962].
Включення коефіцієнтів активності при вирішенні задач рівноваги
Раніше в цьому розділі ми розраховували розчинність Pb (IO 3) 2 в деіонізованій воді, отримавши результат\(4.0 \times 10^{-5}\) моль/л Оскільки єдиним значним джерелом іонів є реакція розчинності, іонна сила дуже низька і можна припустити, що\(\gamma \approx 1\) для обох Pb 2 + і\(\text{IO}_3^-\). При розрахунку розчинності Pb (IO 3) 2 в деіонізованій воді нам не потрібно враховувати іонну силу. Але що робити, якщо нам потрібно знати розчинність Pb (IO 3) 2 в розчині, який містить інші, інертні іони? В цьому випадку нам потрібно включити коефіцієнти активності в наш розрахунок.
Обчисліть розчинність Pb (IO 3) 2 в матриці 0,020 M Mg (NO 3) 2.
Рішення
Починаємо з розрахунку іонної сили розчину. Оскільки Pb (IO 3) 2 є лише помірно розчинним, ми припустимо, що ми можемо ігнорувати його внесок у іонну силу; таким чином
\[\mu=\frac{1}{2}\left\{(0.020)(+2)^{2}+(0.040)(-1)^{2}\right\}=0.060 \ \mathrm{M} \nonumber\]
Далі ми використовуємо Equation\ ref {6.3} для обчислення коефіцієнтів активності для Pb 2+ і\(\text{IO}_3^-\).
\[\log \gamma_{\mathrm{Pb}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.366 \nonumber\]
\[\gamma_{\mathrm{Pb}^{2+}}=0.431 \nonumber\]
\[\log \gamma_{\mathrm{IO}_{3}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.0916 \nonumber\]
\[\gamma_{\mathrm{IO}_{3}^-}=0.810 \nonumber\]
Визначення рівноважних концентрацій Pb 2 + і\(\text{IO}_3^-\) через змінну x
|
Концентрації |
Пб (ІО 3) 2 (и) | \(\rightleftharpoons\) | Пб 2 + (ак) | + | 2\(\text{IO}_3^-\) (кв) |
| ініціал | твердий | 0 | 0 | ||
| змінити | твердий | + х | +2 х | ||
| рівноваги | твердий | х | 2 х |
і заміщення в термодинамічний продукт розчинності для Pb (IO 3) 2 залишає нас
\[K_{\mathrm{sp}}=a_{\mathrm{Pb}^{2+}} \times a_{\mathrm{IO}_{3}^-}^{2}=\gamma_{\mathrm{Pb}^{2+}}\left[\mathrm{Pb}^{2+}\right] \times \gamma_{\mathrm{IO}_3^-}^{2}\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \nonumber\]
\[K_{\mathrm{sp}}=(0.431)(x)(0.810)^{2}(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]
\[K_{\mathrm{sp}}=1.131 x^{3}=2.5 \times 10^{-13} \nonumber\]
Розв'язування для х дає\(6.0 \times 10^{-5}\) і молярну розчинність\(6.0 \times 10^{-5}\) моль/л для Pb (IO 3) 2. Якщо ми ігноруємо активність, як ми робили в нашому попередньому розрахунку, ми повідомляємо про молярну розчинність як\(4.0 \times 10^{-5}\) моль/л, Неврахування активності в цьому випадку занижує молярну розчинність Pb (IO 3) 2 на 33%.
Рівноважний склад розчину
\[\begin{array}{c}{\left[\mathrm{Pb}^{2+}\right]=6.0 \times 10^{-5} \ \mathrm{M}} \\ {\left[\mathrm{IO}_{3}^{-}\right]=1.2 \times 10^{-4} \ \mathrm{M}} \\ {\left[\mathrm{Mg}^{2+}\right]=0.020 \ \mathrm{M}} \\ {\left[\mathrm{NO}_{3}^{-}\right]=0.040 \ \mathrm{M}}\end{array} \nonumber\]
Тому що концентрації як Pb 2 +, так і\(\text{IO}_3^-\) набагато менші, ніж концентрації Mg 2 +, і\(\text{NO}_3^-\) наше рішення ігнорувати внесок Pb 2 + і\(\text{IO}_3^-\) в іонну силу є розумним.
Як ми обробляємо розрахунок, якщо не можемо ігнорувати концентрації Pb 2 + і\(\text{IO}_3^-\) при розрахунку іонної сили. Один з підходів полягає у використанні методу послідовних наближень. Спочатку перерахуємо іонну силу, використовуючи концентрації всіх іонів, включаючи Pb 2 + і\(\text{IO}_3^-\). Далі перераховуємо коефіцієнти активності для Pb 2 + і\(\text{IO}_3^-\) використовуючи цю нову іонну силу, а потім перераховуємо молярну розчинність. Ми продовжуємо цей цикл до тих пір, поки два послідовних обчислення не дадуть однакову молярну розчинність в межах допустимої похибки.
Розрахуйте молярну розчинність Hg 2 Cl 2 в 0,10 М NaCl з урахуванням впливу іонної сили. Порівняйте свою відповідь з тим, що з вправи 6.7.2, в якому ви проігнорували ефект іонної сили.
- Відповідь
-
Починаємо з розрахунку іонної сили розчину. Оскільки NaCl є іонною сіллю 1:1, іонна сила така ж, як і концентрація NaCl; таким чином\(\mu\) = 0,10 М. Це, звичайно, передбачає, що ми можемо ігнорувати внесок\(\text{Hg}_2^{2+}\) і Cl - від розчинності Hg 2 Cl 2.
Далі ми використовуємо Equation\ ref {6.3} для обчислення коефіцієнтів активності для\(\text{Hg}_2^{2+}\) і Cl —.
\[\log \gamma_{\mathrm{Hg}_{2}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.40 \times \sqrt{0.10}}=-0.455 \nonumber\]
\[\gamma_{\mathrm{H} \mathrm{g}_{2}^{2+}}=0.351 \nonumber\]
\[\log \gamma_{\mathrm{Cl}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.3 \times \sqrt{0.10}}=-0.12 \nonumber\]
\[\gamma_{\mathrm{Cl}^-}=0.75 \nonumber\]
Визначення рівноважних концентрацій\(\text{Hg}_2^{2+}\) і Cl — через змінну x
концентрацій Hg2Cl2 (ів) \(\rightleftharpoons\) \(\text{Hg}_2^{2+}\)(aq) + 2Cl — (aq) ініціал твердий 0 0,10 змінити твердий + х +2 х рівноваги твердий х 0,10 + 2 х і замінивши в термодинамічний продукт розчинності для Hg 2 Cl 2, залиште нам
\[K_{\mathrm{sp}}=a_{\mathrm{Hg}_{2}^{2+}}\left(a_{\mathrm{Cl}^-}\right)^{2} = \gamma_{\mathrm{Hg}_{2}^{2+}}\left[\mathrm{Hg}_{2}^{2+}\right]\left(\gamma_{\mathrm{Cl}^{-}}\right)^{2}\left[\mathrm{Cl}^{-}\right]^{2}=1.2 \times 10^{-18} \nonumber\]
Тому що значення х ймовірно мало, давайте спростимо це рівняння до
\[(0.351)(x)(0.75)^{2}(0.1)^{2}=1.2 \times 10^{-18} \nonumber\]
Розв'язування для x дає його значення як\(6.1 \times 10^{-16}\). Оскільки х - це концентрація,\(\text{Hg}_2^{2+}\) а 2 x - концентрація Cl -, наше рішення ігнорувати їх внесок у іонну силу є розумним. Молярна розчинність Hg 2 Cl 2 в 0,10 М NaCl становить\(6.1 \times 10^{-16}\) моль/л У вправі 6.7.2, де ми проігнорували іонну силу, ми визначили, що молярна розчинність Hg 2\(1.2 \times 10^{-16}\) Cl 2 становить моль/л, результат, який\(5 \times\) менше, ніж його фактичне значення.
Як показують приклад Template:index та вправи Template:index, некорекція впливу іонної сили може призвести до значної помилки при розрахунку рівноваги. Тим не менш, незвично ігнорувати діяльність і припустити, що постійна рівноваги виражається в плані концентрацій. Для цього є практична причина - в аналізі ми рідко знаємо точний склад, тим більше іонну силу водних зразків або твердих зразків, внесених у розчин. Розрахунки рівноваги є корисним посібником, коли ми розробляємо аналітичний метод; однак лише тоді, коли ми завершуємо аналіз та оцінюємо результати, ми можемо судити, чи відповідає наша теорія реальності. Зрештою, робота в лабораторії є найбільш відповідальним кроком у розробці надійного аналітичного методу.
Це гарне місце, щоб переглянути значення рН. У главі 2 ми визначили рН як
\[\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]
Тепер ми бачимо, що правильне визначення
\[\begin{array}{c}{\mathrm{pH}=-\log a_{\mathrm{H}_{3} \mathrm{O}^{+}}} \\ {\mathrm{pH}=-\log \gamma_{\mathrm{H}_{3} \mathrm{O}^{+}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\end{array} \nonumber\]
Неврахування ефекту іонної сили може призвести до значної похибки в повідомленій концентрації H 3 O +. Наприклад, якщо рН розчину дорівнює 7,00, а коефіцієнт активності для Н 3 О + 0,90, то концентрація Н 3 О + дорівнює\(1.11 \times 10^{-7}\) М, а не\(1.00 \times 10^{-7}\) М, похибка +11%. На щастя, коли ми розробляємо і виконуємо аналітичний метод, ми більше зацікавлені в контролі рН, ніж в обчисленні [H 3 O +]. В результаті різниця між двома визначеннями рН рідко викликає істотне занепокоєння.
