25.3: Лінійна вольтамметрія розгортки

У найпростішому вольтамметричному експерименті ми застосовуємо лінійну рампу потенціалів як сигнал збудження і записуємо струм, який протікає у відповідь на зміну потенціалу. Серед експериментальних змінних під нашим контролем є початковий потенціал, кінцевий потенціал, швидкість сканування та чи ми вирішили перемішувати розчин або залишати його неперемішаним. Ми називаємо цю лінійну розгортку вольтамметрії.

Щоб проілюструвати, як працює лінійна розгортка вольтамметрія, розглянемо, що відбувається при\(\text{Fe(CN)}_6^{3-}\) зведенні до\(\text{Fe(CN)}_6^{4-}\) на робочому електроді. Зв'язок між концентраціями\(\text{Fe(CN)}_6^{3-}\), концентрацією та потенціалом задається рівнянням Нернста\(\text{Fe(CN)}_6^{4-}\)

\[E=+0.356 \text{ V}-0.05916 \log \frac{\left[\mathrm{Fe}(\mathrm{CN})_{6}^{4-}\right]_{x=0}}{\left[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}\right]_{x=0}} \label{lsv1} \]

де +0,356В - потенціал стандартного стану для\(\text{Fe(CN)}_6^{3-}\)/\(\text{Fe(CN)}_6^{4-}\)окислювально-відновної пари, а x = 0 вказує на те, що концентрації\(\text{Fe(CN)}_6^{3-}\) і\(\text{Fe(CN)}_6^{4-}\) є такими, що знаходяться на поверхні робочого електрода. Ми використовуємо поверхневі концентрації замість об'ємних концентрацій, оскільки положення рівноваги для окислювально-відновної реакції

\[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}(a q)+e^{-}\rightleftharpoons\mathrm{Fe}(\mathrm{CN})_{6}^{4-}(a q) \label{lsv2} \]

встановлюється на поверхні електрода.

Припустимо, що у нас є розчин, для якого початкова концентрація\(\text{Fe(CN)}_6^{3-}\) становить 1,0 мМ і яка\(\text{Fe(CN)}_6^{4-}\) відсутня. \(\PageIndex{1}\)На малюнку показана залежність між прикладеним потенціалом і видами, які стабільні на поверхні електрода.

Малюнок\(\PageIndex{1}\). Діаграма потенціалу\(\text{Fe(CN)}_6^{3-}\)\(\text{Fe(CN)}_6^{4-}\) для/окислювально-відновної напівреакції, що показує потенціали\(\text{Fe(CN)}_6^{4-}\), де\(\text{Fe(CN)}_6^{3-}\) і де переважають види. При потенціалі +0,30 В\(\text{Fe(CN)}_6^{3-}\) стійкий тільки на поверхні електрода.

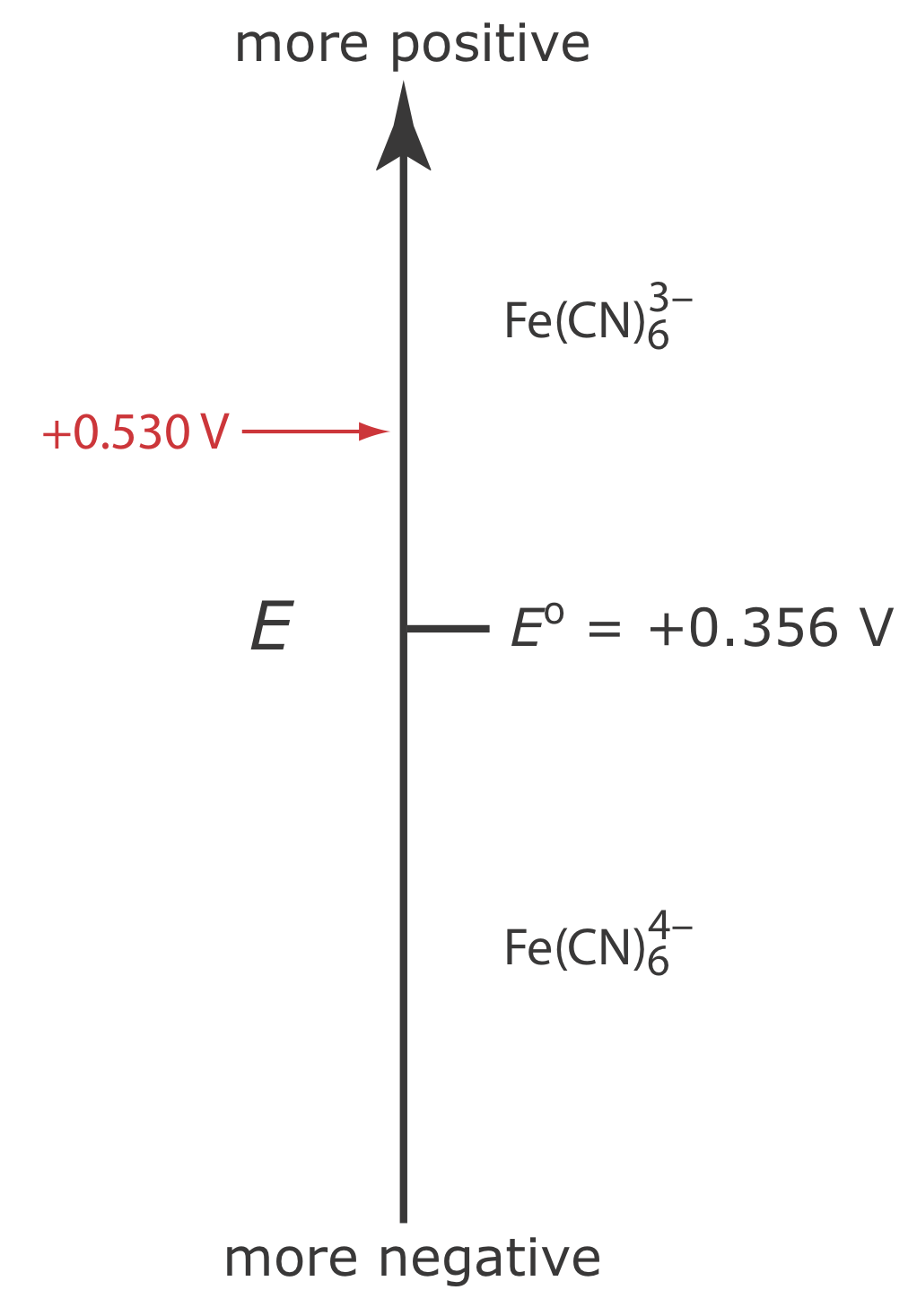
Якщо застосувати до робочого електрода потенціал +0,530 В, концентрації\(\text{Fe(CN)}_6^{3-}\) і\(\text{Fe(CN)}_6^{4-}\) на поверхні електрода не впливають, і фарадаїчний струм не спостерігається. Якщо ми переключимо потенціал на +0,356 В частина\(\text{Fe(CN)}_6^{3-}\) на поверхні електрода зменшується до тих пір,\(\text{Fe(CN)}_6^{4-}\) поки ми не досягнемо умови, коли

\[\left[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}\right]_{x=0}=\left[\mathrm{Fe}(\mathrm{CN})_{6}^{4-}\right]_{x=0}=0.50 \text{ mM} \label{lsv3} \]

Якщо це все, що відбувається після того, як ми застосуємо потенціал, то стався б нетривалий сплеск фарадаїчного струму, який швидко повертається до нуля, що не є найцікавішим з результатів (хоча це основа для хроноамперометрії, електрохімічного методу ми розглядати в цьому тексті не будемо). Хоча концентрації\(\text{Fe(CN)}_6^{3-}\) і\(\text{Fe(CN)}_6^{4-}\) на поверхні електрода становлять 0,50 мМ, їх концентрації в об'ємному розчині залишаються незмінними.

Через цю різницю в концентрації існує градієнт концентрації між поверхнею електрода і об'ємним розчином. Цей градієнт концентрації створює рушійну силу, яка транспортується\(\text{Fe(CN)}_6^{4-}\) від електрода і транспортується\(\text{Fe(CN)}_6^{3-}\) до електрода (рис.\(\PageIndex{2}\)). У міру\(\text{Fe(CN)}_6^{3-}\) надходження на електрод він теж зводиться до\(\text{Fe(CN)}_6^{4-}\). Фарадаїчний струм продовжує протікати до тих пір, поки не буде різниці між концентраціями\(\text{Fe(CN)}_6^{3-}\) і\(\text{Fe(CN)}_6^{4-}\) на електроді та їх концентраціями в об'ємному розчині (хоча це може зайняти багато часу!).

Малюнок\(\PageIndex{2}\). Принципова схема, що показує транспортування\(\text{Fe(CN)}_6^{4-}\) від поверхні електрода та\(\text{Fe(CN)}_6^{3-}\) транспортування до поверхні електрода після зменшення\(\text{Fe(CN)}_6^{3-}\) до\(\text{Fe(CN)}_6^{4-}\).

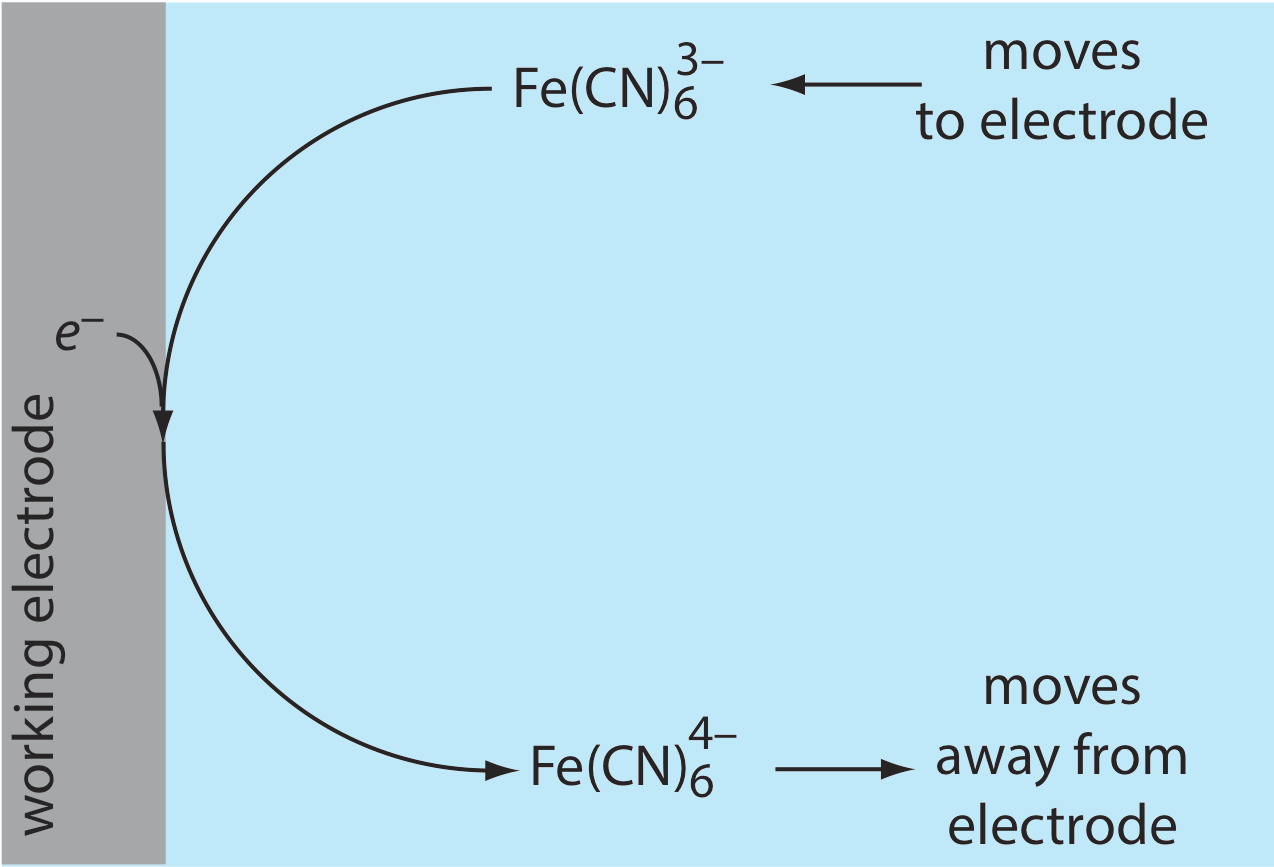
Хоча потенціал у робочого електрода визначає, чи тече фарадаїчний струм, величина струму визначається швидкістю одержуваної реакції окислення або відновлення. Швидкість електрохімічної реакції сприяє два фактори: швидкість, з якою реагенти та продукти транспортуються до електрода та від електрода - те, що ми називаємо масовим транспортом, - і швидкість, з якою електрони проходять між електродом та реагентами та продуктами в розчині.

Профілі концентрації на робочому електроді

Існує три способи транспортування маси, які впливають на швидкість переміщення реагентів та продуктів у напрямку або від поверхні електрода: дифузія, міграція та конвекція. Дифузія відбувається всякий раз, коли концентрація іона або молекули на поверхні електрода відрізняється від концентрації в об'ємному розчині. Якщо застосувати потенціал, достатній для повного зменшення\(\text{Fe(CN)}_6^{3-}\) на поверхні електрода, результатом буде градієнт концентрації, подібний до показаного на малюнку\(\PageIndex{3}\). Область розчину, над якою відбувається дифузія, є дифузійний шар. За відсутності інших видів масового транспорту ширина дифузійного шару збільшується з часом\(\delta\), оскільки\(\text{Fe(CN)}_6^{3-}\) повинен розсіюватися зі все більшої відстані.

Малюнок\(\PageIndex{3}\). Градієнти концентрації (червоним кольором) для\(\text{Fe(CN)}_6^{3-}\) подальшого застосування потенціалу, який повністю знижує його до\(\text{Fe(CN)}_6^{4-}\). Перед тим як застосувати потенціал (t = 0) концентрація\(\text{Fe(CN)}_6^{3-}\) однакова на всіх відстанях від поверхні електрода. Після того як ми застосуємо потенціал, його концентрація на поверхні електрода зменшується до нуля і\(\text{Fe(CN)}_6^{3-}\) дифундує на електрод з об'ємного розчину. Чим довше ми застосовуємо потенціал, тим більше відстань, на якому відбувається дифузія. Пунктирна червона лінія показує протяжність дифузійного шару в момент t ₃. Ці профілі припускають, що конвекція і міграція не сприяють суттєво масовому транспортуванню\(\text{Fe(CN)}_6^{3-}\).

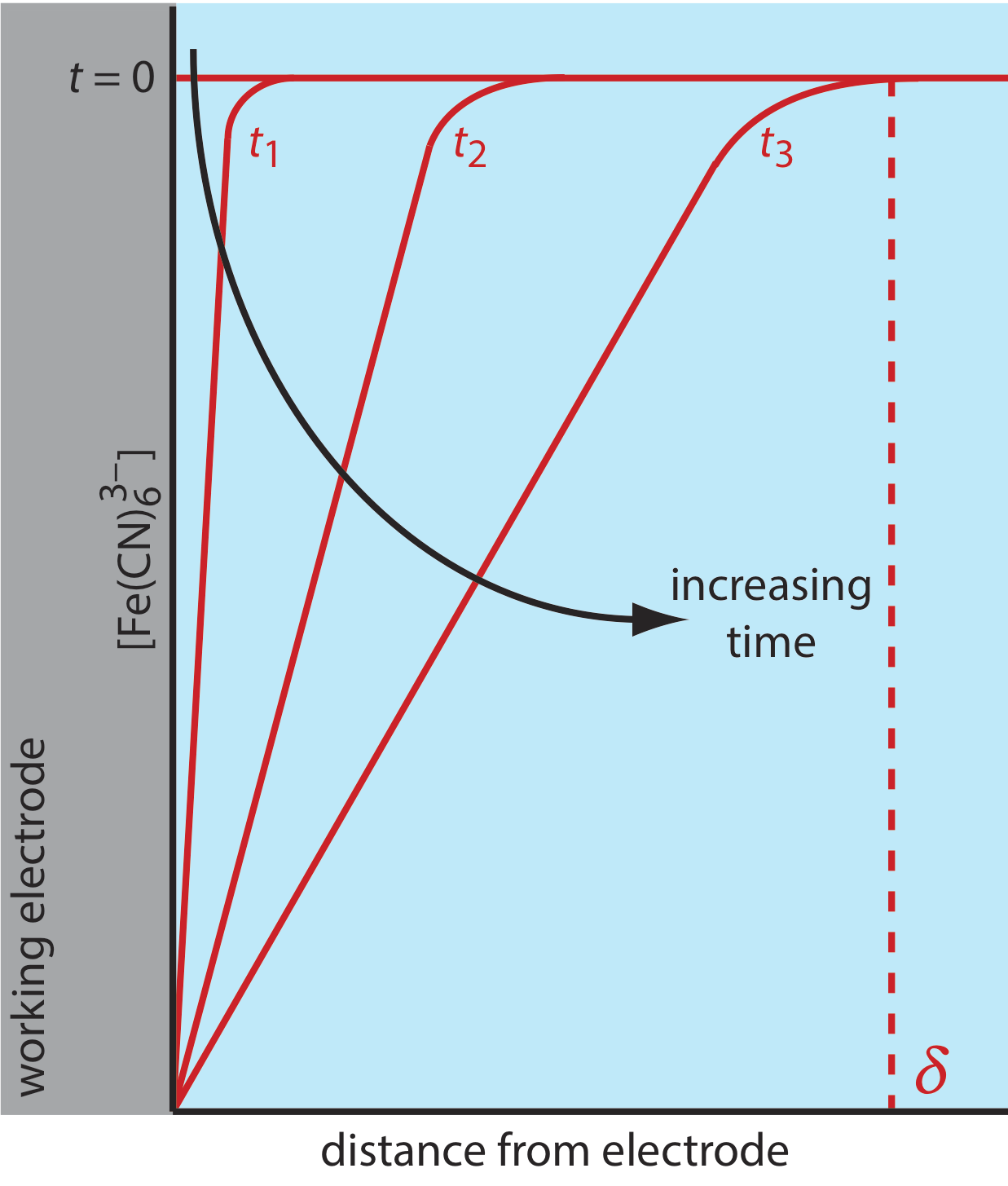
Конвекція виникає при перемішуванні розчину, який переносить реагенти в сторону електрода і видаляє продукти з електрода. Найбільш поширеною формою конвекції є перемішування розчину з мішалкою; інші методи включають обертання електрода і включення електрода в проточну комірку.

Кінцевим способом транспортування маси є міграція, яка відбувається, коли заряджена частинка в розчині притягується або відштовхується від електрода, який несе поверхневий заряд. Якщо електрод несе позитивний заряд, наприклад, аніон буде рухатися до електрода і катіон буде рухатися в бік об'ємного розчину. На відміну від дифузії і конвекції, міграція впливає тільки на масовий транспорт заряджених частинок.

Рух матеріалу до поверхні електрода і від неї є складною функцією всіх трьох видів масового транспорту. У межі, де дифузія є єдиною значущою формою масового транспорту, струм\(i\), у вольтамметричній комірці пропорційний нахилу профілю концентрації на рис.\(\PageIndex{3}\)

\[i \propto \frac {\partial C} {\partial x} \label{lsv4} \]

де\(C\) -\(x\) концентрація\(\text{Fe(CN)}_6^{3-}\) і відстань.

Щоб Equation\ ref {lsv4} був дійсним, конвекція та міграція не повинні перешкоджати утворенню дифузійного шару. Ми можемо усунути міграцію, додавши високу концентрацію інертного підтримуючого електроліту. Оскільки іони подібного заряду однаково притягуються до поверхні електрода або відштовхуються від неї, кожен має рівну ймовірність зазнати міграції. Великий надлишок інертного електроліту гарантує, що мало реагентів або продуктів відчувають міграцію. Хоча легко усунути конвекцію, не перемішуючи розчин, існують експериментальні конструкції, де ми не можемо уникнути конвекції, або тому, що ми повинні перемішувати розчин, або тому, що ми використовуємо електрохімічну проточну комірку. На щастя, як показано на малюнку\(\PageIndex{4}\), динаміка рідини, що рухається повз електрода, призводить до невеликого дифузійного шару - як правило, товщиною 1-10 мкм - в якому швидкість транспортування маси конвекцією падає до нуля.

Малюнок\(\PageIndex{4}\). Градієнт концентрації\(\text{Fe(CN)}_6^{3-}\) при перемішуванні розчину. Дифузія є єдиною значущою формою транспортування маси близько до поверхні електрода. На відстанях більше\(\delta\), ніж, конвекція є єдиною значущою формою масового транспорту, підтримуючи однорідний розчин, в якому концентрація\(\text{Fe(CN)}_6^{3-}\) ат\(\delta\) така ж, як і його концентрація в насипному розчині.

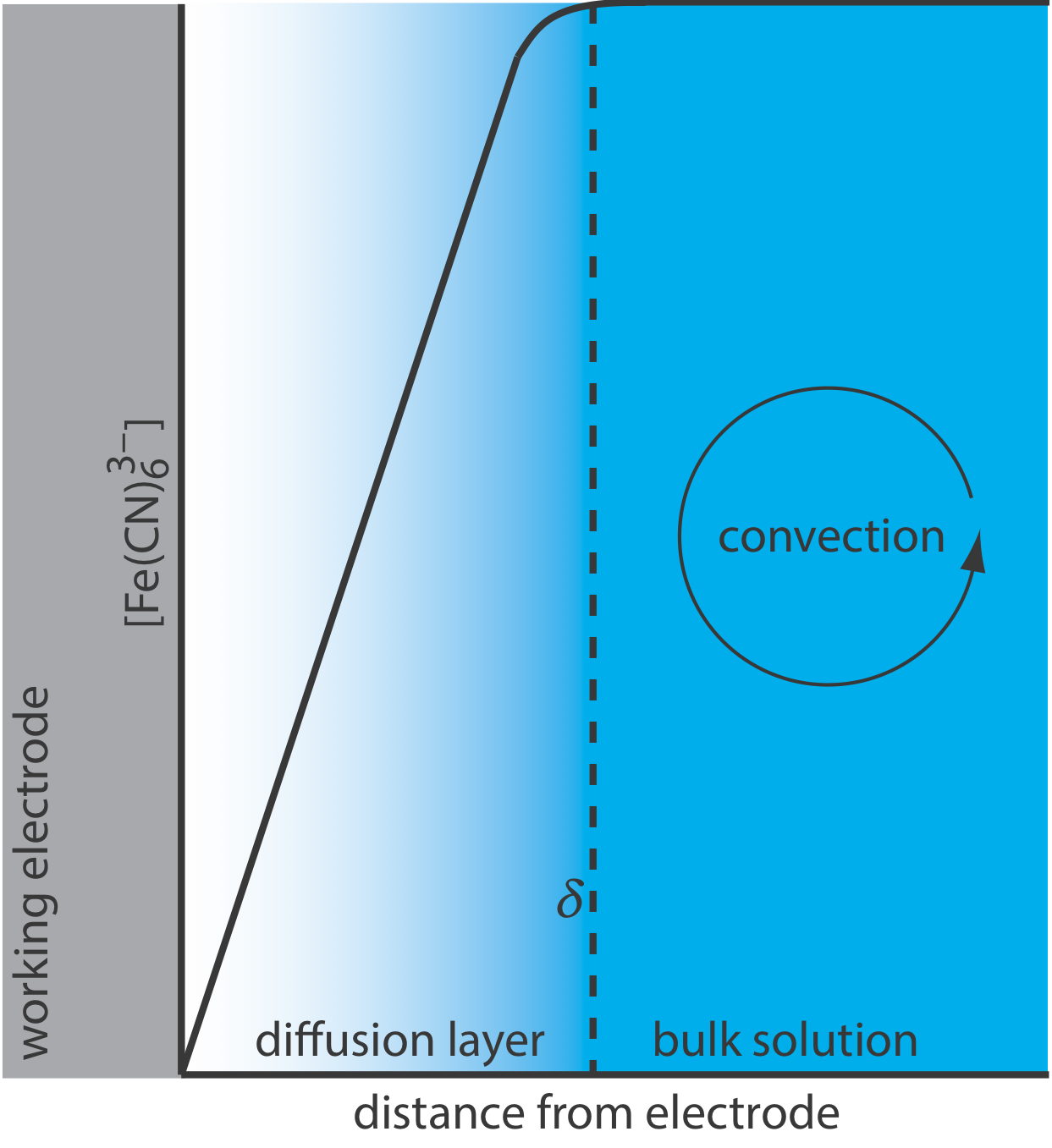
Профілі концентрації в неперемішаному розчині

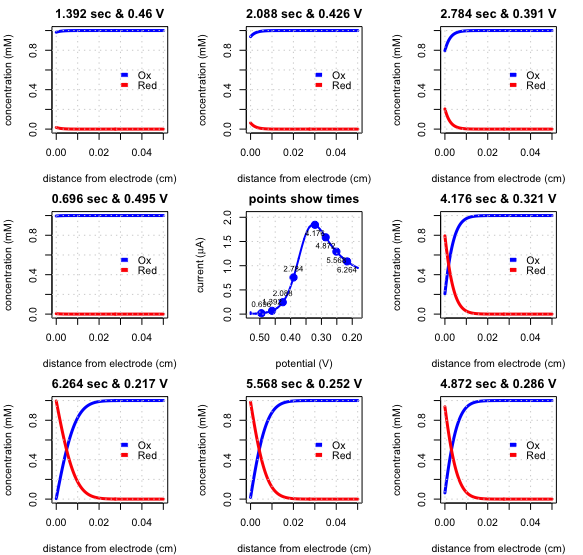
\(\PageIndex{5}\)На малюнку показана лінійна вольтаммограма розгортки (центральне зображення, яке показує струм як функцію часу) і вісім знімків профілів концентрації для зменшення\(\text{Fe(CN)}_6^{3-}\) до\(\text{Fe(CN)}_6^{4-}\) в неперемішаному розчині. Початковий потенціал був встановлений на рівні +0,530 В, а кінцевий потенціал був встановлений на +0,182 В зі швидкістю сканування 0,050 В/с.

При початковому потенціалі тільки\(\text{Fe(CN)}_6^{3-}\) стабільний на поверхні електрода, і струм не тече. Через 0,696 с потенціал становить 0,495 В (зображення зліва від лінійної вольтаммограми розгортки) і, оскільки\(\text{Fe(CN)}_6^{3-}\) залишається стабільним на поверхні електрода, струм не тече. Рухаючись за годинниковою стрілкою навколо лінійної розгортки вольтаммограми, прикладений потенціал стає менше і концентрація\(\text{Fe(CN)}_6^{3-}\) на поверхні електрода зменшується і концентрація\(\text{Fe(CN)}_6^{4-}\) збільшується. Спочатку нахил градієнта концентрації, а, отже, збільшується струм; у міру наближення концентрації\(\text{Fe(CN)}_6^{3-}\) на поверхні електрода до нуля, однак градієнт концентрації стає менш крутим і струм зменшується. Результатом є лінійна розгортка вольтаммограми в центрі діаграми.

Малюнок\(\PageIndex{5}\): На центральному зображенні показана лінійна вольтаммограма розгортки в неперемішуваному розчині для зменшення\(\text{Fe(CN)}_6^{3-}\) до\(\text{Fe(CN)}_6^{4-}\). Решта зображень показують профілі концентрації для\(\text{Fe(CN)}_6^{3-}\) (синім кольором) та для\(\text{Fe(CN)}_6^{4-}\) (червоним кольором), оскільки потенціал змітається від +0.530 В до +0.182 В (розташовані за годинниковою стрілкою, починаючи відразу ліворуч від лінійної вольтаммограми розгортки.

Профілі концентрації в перемішаному розчині

Якщо ми проведемо той же експеримент, що і на малюнку\(\PageIndex{5}\), але перемішуємо розчин, отримані лінійні вольтаммограми розгортки і профілі концентрації є такими, як на рис\(\PageIndex{6}\). Перемішування розчину, як ми бачили на малюнку,\(\PageIndex{4}\) створює дифузійний шар, товщина якого не залежить від часу.

Малюнок\(\PageIndex{6}\): На центральному зображенні показана лінійна вольтаммограма розгортки в перемішуваному розчині для зменшення\(\text{Fe(CN)}_6^{3-}\) до\(\text{Fe(CN)}_6^{4-}\). Решта зображень показують профілі концентрації для\(\text{Fe(CN)}_6^{3-}\) (синім кольором) та для\(\text{Fe(CN)}_6^{4-}\) (червоним кольором), оскільки потенціал змітається від +0.530 В до +0.182 В (розташовані за годинниковою стрілкою, починаючи відразу ліворуч від лінійної вольтаммограми розгортки.

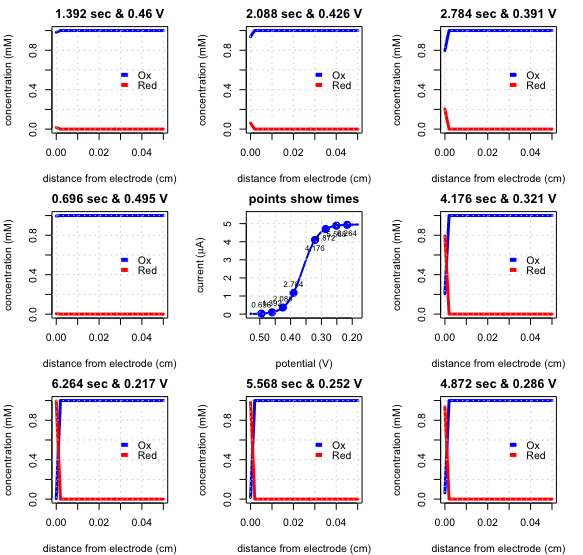
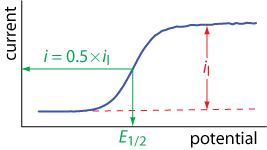
В результаті замість пікового струму на малюнку\(\PageIndex{5}\) струм досягає сталого значення, яке ми називаємо граничним струмом,\(i_l\). Лінійна вольтаммограма розгортки також має характерний напівхвильовий потенціал\(E_{1/2}\), коли струм становить 50% граничного струму. На малюнку\(\PageIndex{7}\) показано, як вимірюється граничний струм і напівхвильовий потенціал.

Рисунок\(\PageIndex{7}\): Граничний струм і напівхвильовий потенціал для лінійного експерименту вольтамметрії розгортки в перемішуваному розчині.

Вольтамметричні струми

Раніше ми відзначали в Equation\ ref {lsv4}, що струм в лінійній вольтамметрії розгортки пропорційний нахилу профілю концентрації. Струм також є функцією інших змінних, як показано тут для зменшення\(\text{Fe(CN)}_6^{3-}\) до\(\text{Fe(CN)}_6^{4-}\)

\[i = \frac{ n F A D \left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right)} {\delta} \label{lsv5} \]

де n число електронів в окисно-відновній реакції, F - постійна Фарадея, A - площа електрода, D - коефіцієнт дифузії для\(\text{Fe(CN)}_6^{3-}\),\(\delta\) - товщина дифузійного шару, і\(\left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right)\) є різницею в концентрація\( \ce{Fe(CN)6^{3-}}\) між об'ємним розчином і поверхнею електрода.

Тому що\(n\),\(F\),\(A\), і\(D\) є константами, і тому що\(\delta\) є константою, якщо ми перемішуємо рішення, ми можемо записати Equation\ ref {lsv5} як

\[i = K_{\ce{Fe(CN)6^{3-}}} \left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right) \label{lsv6} \]

де\(K_{\ce{Fe(CN)6^{3-}}}\) - константа. Якщо використовувати граничний струм, то\(\left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0}\) дорівнює нулю, а Equation\ ref {lsv6} стає

\[i_l = K_{\ce{Fe(CN)6^{3-}}} \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} \label{lsv7} \]

Відносини струму/напруги для оборотних реакцій

Оборотна електрохімічна реакція - це така, при якій концентрації окислених і відновлених видів на поверхні електрода залишаються в термодинамічній рівновазі один з одним. Коли це вірно, рівняння Нернста пояснює взаємозв'язок між прикладним потенціалом, їх концентрацією та стандартним потенціалом стану.

Рівняння\ ref {lsv7} показує нам, що граничний струм є мірою концентрації\(\text{Fe(CN)}_6^{3-}\) в об'ємному розчині, а значить, ми можемо використовувати граничний струм для кількісної роботи. Малюнок\(\PageIndex{7}\) також показує, що існує якісна залежність між півхвильовим\(E_{1/2}\) потенціалом і граничним струмом; однак поки не зрозуміло, що являє собою напівхвильовий потенціал.

Якщо ми вирішимо рівняння\ ref {lsv7} для\(\left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} \) і підставимо в Equation\ ref {lsv6} і переставляємо, ми маємо

\[ \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} = \frac {i_l - i} {K_{\ce{Fe(CN)6^{3-}}}} \label{lsv8} \]

Якщо взяти такий же підхід з тим\(\text{Fe(CN)}_6^{4-}\), який утворюється при електроді розчин, то маємо

\[i = -\frac{ n F A D \left( \left[ \ce{Fe(CN)6^{4-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} \right)} {\delta} = K_{\ce{Fe(CN)6^{4-}}} \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} \label{lsv9} \]

\[ \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} = \frac {-i} {K_{\ce{Fe(CN)6^{4-}}}} \label{lsv10} \]

де знак мінус припадає на профіль концентрації, що має негативний нахил. Підставляючи рівняння\ ref {lsv9} та рівняння\ ref {lsv10} на рівняння\ ref {lsv1}, яке є рівнянням Нерснта, дає

\[E = E^{\circ} - 0.05916 \log \frac {-i/K_{\ce{Fe(CN)6^{4-}}}} {(i_l - i)/K_{\ce{Fe(CN)6^{3-}}}} \label{lsv11} \]

\[E = E^{\circ} + 0.05916 \log \frac{K_{\ce{Fe(CN)6^{3-}}}}{K_{\ce{Fe(CN)6^{4-}}}} - 0.05916 \log \frac {i} {i_l - i} \label{lsv12} \]

Коли\(i = \frac {i_l - i} {2}\), яке є визначенням\(E_{1/2}\), Equation\ ref {lsv12} спрощує

\[E_{1/2} = E^{\circ} + 0.05916 \log \frac{K_{\ce{Fe(CN)6^{3-}}}}{K_{\ce{Fe(CN)6^{4-}}}} \label{lsv13} \]

Єдиною відмінністю між\(K_{\ce{Fe(CN)6^{3-}}}\) і\(K_{\ce{Fe(CN)6^{4-}}}\) є коефіцієнти дифузії\(D\),, for\(\ce{Fe(CN)6^{3-}}\) і for\(\ce{Fe(CN)6^{4-}}\). Оскільки ці значення повинні бути схожими, ми маємо

\[E_{1/2} \approx E^{\circ} \label{lsv14} \]

та\(E_{1/2}\) дає оцінку нормативного потенціалу державного скорочення.

Взаємовідносини струму/напруги для незворотних реакцій

Коли електрохімічна реакція не є оборотною, рівняння Нернста більше не застосовується, а це означає, що ми більше не можемо вважати, що напівхвильовий потенціал забезпечує оцінку потенціалу відновлення стандартного стану. Взаємозв'язок між граничним струмом і концентрацією електроактивних видів в об'ємному розчині все ще зберігається, і кількісна робота залишається можливою.

кисневі хвилі

Наявність розчиненого кисню створює ускладнення, оскільки він здатний зазнати реакцій відновлення на поверхні електрода, які можуть перешкоджати визначенню граничного струму або півхвильового потенціалу аналіта. Наприклад, О ₂ знижується до Н ₂ О ₂ зі стандартним потенціалом стану +0,695 В

\[\ce{O2}(g) + 2\ce{H+}(aq) + 2e^{-} \rightleftharpoons \ce{H2O2}(aq) \label{lsv15} \]

а Н ₂ О ₂ згодом знижується до Н ₂ О при стандартному стані потенціалу +1,763 В.

\[\ce{H2O2}(aq) + 2\ce{H+}(aq) + 2e^{-} \rightleftharpoons 2 \ce{H2O}(aq) \label{lsv16} \]

Це є причиною того, що типова осередок для вольтамметрії (див. Рис. 25.2.5) включає здатність пропускати через розчин N ₂ для видалення розчиненого О ₂. Після деаерації розчину N ₂ дають текти над розчином, щоб запобігти повторному надходженню O ₂ в розчин.

Застосування лінійної стрілочної вольтамметрії

Як ми дізналися в попередньому розділі, граничний струм в лінійної розгортки вольтамметрії пропорційний концентрації видів, що піддаються окисленню або відновленню на поверхні електрода, що робить його корисним інструментом для кількісного аналізу. Оскільки нас цікавить тільки граничний струм, більшість кількісних методів просто утримують потенціал робочого електрода на фіксованій величині і вимірюють граничний струм. Оскільки ми вимірюємо струм як функцію часу замість потенціалу, вони називаються амперометричними методами (де ампер - одиниця струму). Тут зібрано кілька прикладів амперометичних методів.

Амперометричні детектори в хроматографії та проточно-ін'єкційному аналізі

Один важливий детектор для високоефективної рідинної хроматографії (ВЕРХ), в якому рухлива фаза, що елюює з колони, проходить через електрохімічну комірку невеликого обсягу, в якій робочий електрод утримується з потенціалом, який буде окислювати або зменшувати аналіти. Отриманий струм наноситься як функція часу для виходу хроматограми. Подібне розташування використовується в проточно-ін'єкційному аналізі (FIA). Докладніше див. Розділ 28 (ВЕРХ) та главу 33 (FIA).

Амперометричні датчики

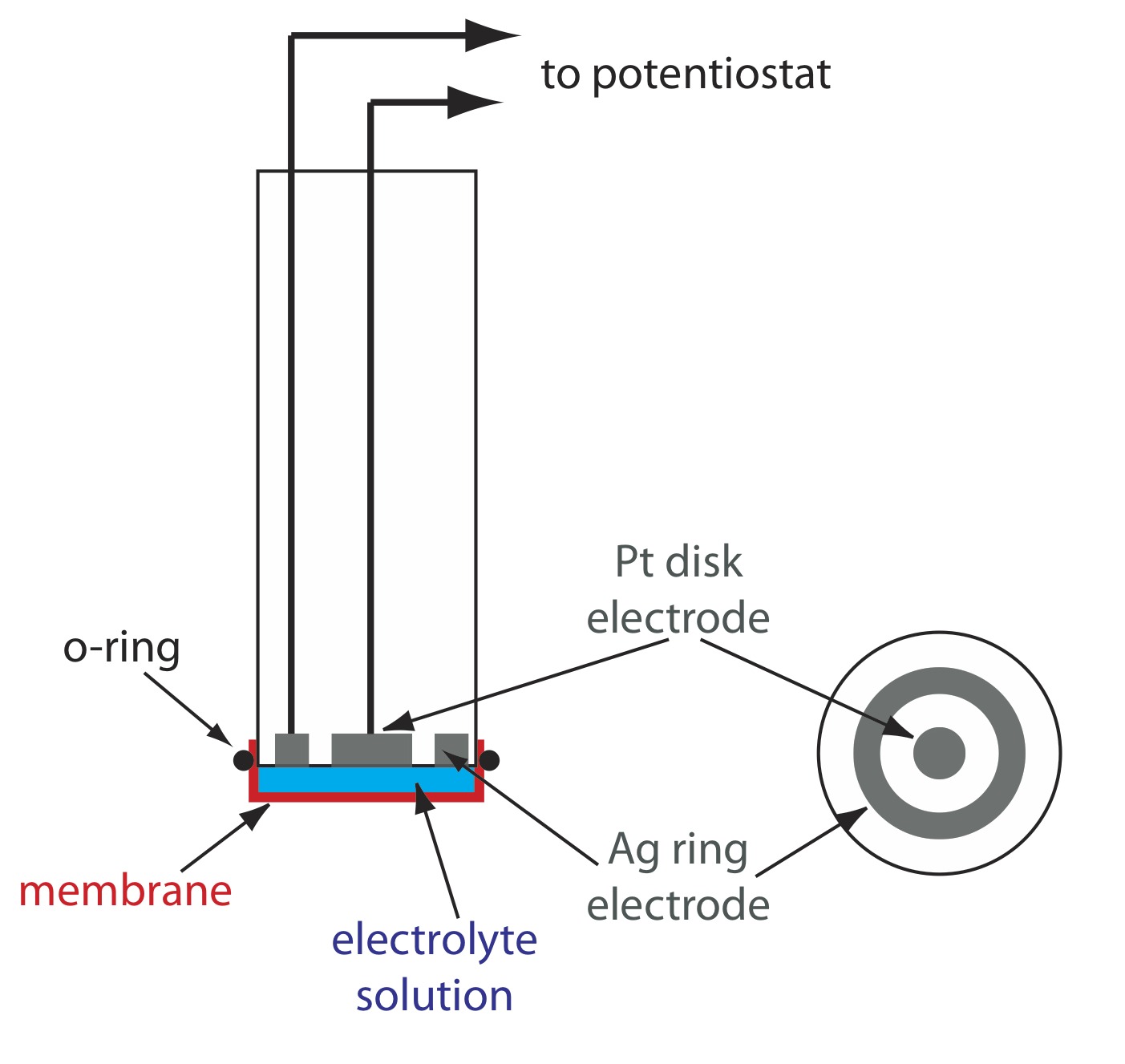
Одним з важливих застосувань амперометрії є побудова хімічних датчиків. Один з перших амперометричних датчиків був розроблений в 1956 році Л.К. Кларком для вимірювання розчиненого O ₂ в крові. \(\PageIndex{9}\)На малюнку показана конструкція датчика, яка схожа на потенціометричний мембранний електрод. Тонка газопроникна мембрана натягнута поперек кінця датчика і відокремлюється від робочого електрода і зустрічного електрода тонким розчином KCl. Робочий електрод являє собою дисковий катод Pt, а кільцевим анодом Ag служить зустрічним електродом. Хоча кілька газів можуть дифузувати по мембрані, включаючи O ₂, N ₂ і CO ₂, тільки кисень піддається відновленню на катоді

\[\mathrm{O}_{2}(g)+4 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+4 e^{-}\rightleftharpoons 6 \mathrm{H}_{2} \mathrm{O}(l) \label{lsv17} \]

при цьому його концентрація на поверхні електрода швидко досягає нуля. Концентрація О ₂ на внутрішній поверхні мембрани фіксується її дифузією через мембрану, яка створює граничний струм. В результаті виходить стійкий струм, пропорційний концентрації розчиненого кисню. Оскільки електрод споживає кисень, зразок перемішують, щоб запобігти виснаженню O ₂ на зовнішній поверхні мембрани.

Окислення анода Ag - це інша напівреакція.

\[\mathrm{Ag}(s)+\text{ Cl}^{-}(a q)\rightleftharpoons \mathrm{AgCl}(s)+e^{-} \nonumber \]

Малюнок\(\PageIndex{9}\). Амперометричний датчик Кларка для визначення розчиненого O ₂. Діаграма праворуч - це поперечний переріз через електрод, на якому зображений кільцевий електрод Ag і дисковий електрод Pt.

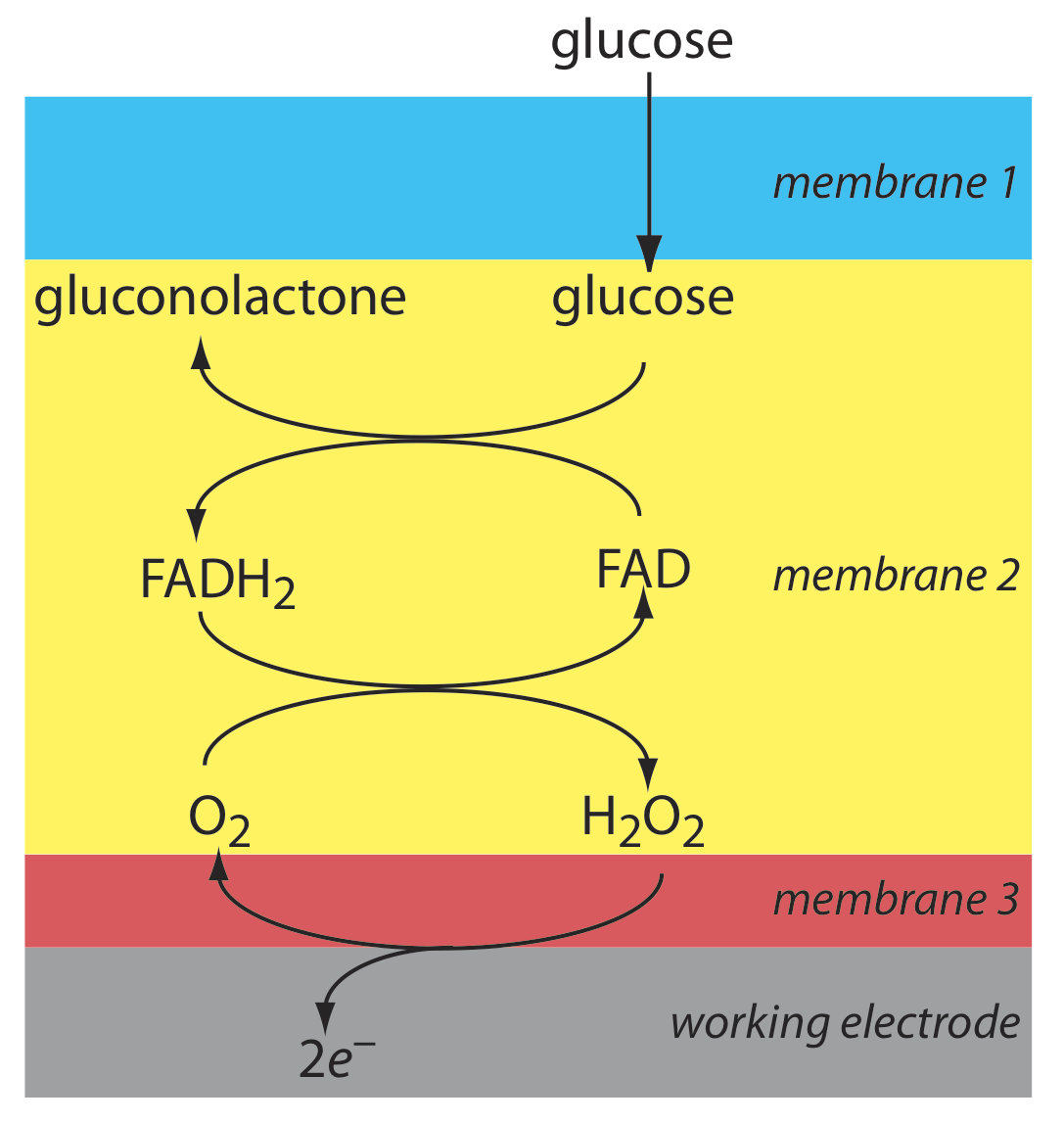
Ще один приклад амперометричного датчика - датчик глюкози. У цьому датчику одна мембрана на малюнку\(\PageIndex{10}\) замінена трьома мембранами. Сама зовнішня мембрана з полікарбонату проникна для глюкози і O ₂. Друга мембрана містить іммобілізований препарат глюкозоксидази, який каталізує окислення глюкози до глюконолактону і перекису водню.

\[\beta-\mathrm{D}-\text {glucose }(a q)+\text{ O}_{2}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \text {gluconolactone }(a q)+\text{ H}_{2} \mathrm{O}_{2}(a q) \label{lsv18} \]

Перекис водню дифундує через внутрішню мембрану ацетату целюлози, де вона піддається окисленню на аноді Pt.

\[\mathrm{H}_{2} \mathrm{O}_{2}(a q)+2 \mathrm{OH}^{-}(a q) \rightleftharpoons \text{ O}_{2}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)+2 e^{-} \label{lsv19} \]

На малюнку\(\PageIndex{10}\) підсумовуються реакції, які відбуваються в цьому амперометричному датчику. FAD - це окислена форма флавінового аденіннуклеотиду - активного місця ферменту оксидази глюкози - і FADH ₂ є відновленою формою активного сайту. Відзначимо, що О ₂ служить медіатором, несучи електрони до електрода.

Малюнок\(\PageIndex{10}\). Схема, що показує реакції, за допомогою яких амперометричний біосенсор реагує на глюкозу.

Змінюючи фермент і медіатор, легко поширюється на амперометричний датчик на малюнку\(\PageIndex{10}\) до аналізу інших аналітів. Наприклад, датчик СО ₂ був розроблений з використанням амперометричного датчика O ₂ з двошаровою мембраною, один з яких містить іммобілізований препарат автотрофних бактерій [Karube, I.; Nomura, Y; Arikawa, Y.Trends in Anal. Хім. 1995, 14, 295-299]. У міру дифузії CO ₂ через мембрани він перетворюється в O ₂ бактеріями, збільшуючи концентрацію O ₂ на катоді Pt.