4.2: MATLAB та незалежні класи
- Page ID
- 98585
MATLAB та незалежні класи
У одиниці на Мінтермах показано, як використовувати мінтермальні ймовірності та мінтермові вектори для обчислення ймовірностей булевих комбінацій подій. В Independence of Events ми показуємо, що в незалежному випадку ми можемо обчислити всі мінтермальні ймовірності з ймовірностей основних подій. Хоча ці розрахунки прості, вони можуть бути виснажливими і схильні до помилок. На щастя, у цьому випадку у нас є m-функція minprob, яка обчислює всі мінтермальні ймовірності з ймовірностей базових або генеруючих наборів. Ця функція використовує m-функцію mintable для налаштування шаблонів з і\(p\) '\(q\)s для різних minterms, а потім приймає продукти, щоб отримати набір minterm ймовірностей.
Приклад\(\PageIndex{1}\)
>> pm = minprob(0.1*[4 7 6]) pm = 0.0720 0.1080 0.1680 0.2520 0.0480 0.0720 0.1120 0.1680
Можливо, бажано розташувати їх як на мінтермальній карті. Для цього ми маємо m-функцію minmap, яка змінює матрицю\(pm\) рядків наступним чином:
>> t = minmap(pm)
t = 0.0720 0.1680 0.0480 0.1120
0.1080 0.2520 0.0720 0.1680
Імовірність виникнення k n незалежних подій
У прикладі 2 показано, як використовувати m-функції mintable та csort для отримання ймовірності\(k\) виникнення\(n\) подій, коли доступні мінтермальні ймовірності. У випадку з незалежним класом, мінтермальні ймовірності легко обчислюються мінпроб, необхідно лише вказати ймовірності для\(n\) основних подій і номери\(k\) подій. Визначається розмір класу, звідси і mintable, а мінтермальні ймовірності обчислюються minprob. У нас є дві корисні m-функції. Якщо\(P\) є матрицею ймовірностей\(n\) окремих подій, і\(k\) є матрицею цілих чисел менше або дорівнює\(n\), то
функція\(y = \text{ikn}(P, k)\) обчислює індивідуальні\(k\) ймовірності, що\(n\) відбуваються
функція\(y = \text{ckn}(P, k)\) обчислює ймовірності, які виникають\(k\) або більше
Приклад\(\PageIndex{2}\)
>> p = 0.01*[13 37 12 56 33 71 22 43 57 31]; >> k = [2 5 7]; >> P = ikn(p,k) P = 0.1401 0.1845 0.0225 % individual probabilities >> Pc = ckn(p,k) Pc = 0.9516 0.2921 0.0266 % cumulative probabilities
Надійність систем з незалежними компонентами
Припустимо, система має\(n\) компоненти, які виходять з ладу самостійно. \(E_i\)Дозволяти подією, коли компонент\(i\) th переживає зазначений період часу. Тоді\(R_i = P(E_i)\) визначається як надійність цього компонента. \(R\)Надійність повної системи - це функція надійності компонентів. Існує три основні конфігурації. Загальні системи можуть бути розкладені на підсистеми цих типів. Підсистеми стають компонентами більшої конфігурації. Три основні конфігурації:
Серія. Система працює, якщо працюють всі n компонентів:\(R = \prod_{i = 1}^n R_i\)
Паралельний. Система працює, якщо не всі компоненти виходять з ладу:\(R = 1 - \prod_{i = 1}^{n} (1 - R_i)\)
k п. Система працює, якщо працює\(k\) більше компонентів. \(R\)можна обчислити за допомогою m-функції cn. Якщо ймовірності компонента однакові, ефективніше використовувати m-функцію cbinom (див. Проби Бернуллі та біноміальний розподіл нижче).
Рішення MATLAB. Помістіть надійність компонента в матрицю\(RC = [R_1\ R_2\ \cdot\cdot\cdot \ R_n]\)
Конфігурація серії
>> R = prod(RC) % prod is a built in MATLAB function
Паралельна конфігурація
>> R = parallel(RC) % parallel is a user defined function
k або n Конфігурація
>> R = ckn(RC,k) % ckn is a user defined function (in file ckn.m).
Приклад\(\PageIndex{3}\)
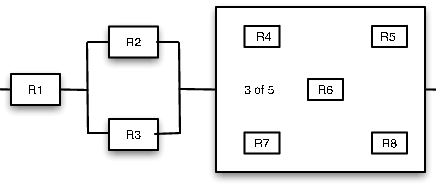
Існує вісім компонентів, пронумерованих від 1 до 8. Компонент 1 послідовно з паралельним поєднанням компонентів 2 і 3 з подальшим поєднанням 3 з 5 компонентів 4 по 8 (схематичне зображення див. Рис. Ймовірності компонентів в порядку є
0,95 0,90 0,92 0,80 0,83 0,91 0,85 0,85
Друга і третя ймовірності - для паралельної пари, а останні п'ять ймовірностей - для комбінації 3 з 5.
>> RC = 0.01*[95 90 92 80 83 91 85 85]; % Component reliabilities >> Ra = RC(1)*parallel(RC(2:3))*ckn(RC(4:8),3) % Solution Ra = 0.9172
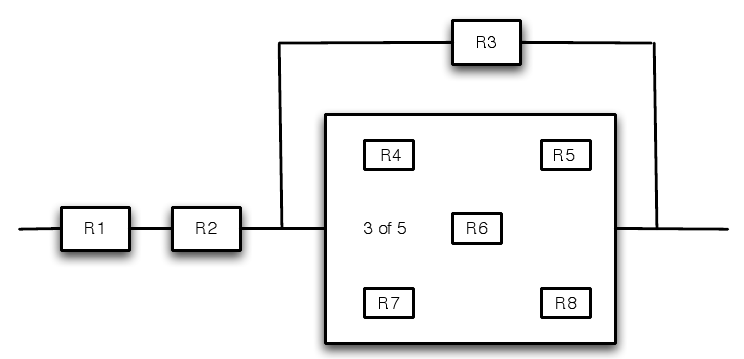
Приклад\(\PageIndex{4}\)
>> RC = 0.01*[95 90 92 80 83 91 85 85]; % Component reliabilities 1--8 >> Rb = prod(RC(1:2))*parallel([RC(3),ckn(RC(4:8),3)]) % Solution Rb = 0.8532
Тест на незалежність
Важко подивитися на список мінтермальних ймовірностей і визначити, утворюють чи генеруючі події незалежний клас. M-функція imintest має як аргумент вектор мінтермальних ймовірностей. Він перевіряє можливий розмір, визначає кількість змінних і виконує перевірку на незалежність.
Приклад\(\PageIndex{5}\)
>> pm = 0.01*[15 5 2 18 25 5 18 12]; % An arbitrary class
>> disp(imintest(pm))
The class is NOT independent
Minterms for which the product rule fails
1 1 1 0
1 1 1 0
Приклад\(\PageIndex{6}\)
>> pm = [0.10 0.15 0.20 0.25 0.30]: %An improper number of probabilities >> disp(imintest(pm)) The number of minterm probabilities incorrect
Приклад\(\PageIndex{7}\)
>> pm = minprob([0.5 0.3 0.7]); >> disp(imintest(pm)) The class is independent
Імовірності булевих комбінацій
Як і в ненезалежному випадку, ми можемо використовувати мінтермальне розширення та мінтермальні ймовірності для обчислення ймовірностей булевих комбінацій подій. Однак часто ефективніше маніпулювати виразами для логічної комбінації, щоб бути неспільним об'єднанням перетинів.
Приклад\(\PageIndex{8}\) A simple Boolean combination
Припустимо, клас {\(A\)\(B\),,\(C\)} є незалежним, з відповідними ймовірностями 0,4, 0,6, 0,8. Визначте\(P(A \cup BC)\). Довгострокова експансія - це
\(A \cup BC = M(3, 4, 5, 6, 7)\), so that \(P(A \cup BC) = p(3, 4, 5, 6, 7)\)
Неважко використовувати правило продукту та теорему заміни для обчислення необхідних мінтермальних ймовірностей. Таким чином\(p(3) = P(A^c) P(B) = P(C) = 0.6 \cdot 0.6 \cdot 0.8 = 0.2280\). Аналогічно\(p(4) = 0.0320\)\(p(5) = 0.1280\),\(p(6) = 0.0480\),,\(p(7) = 0.1920\). Бажана ймовірність - це сума цих, 0.6880.
Як альтернативний підхід пишемо
\(A \cup BC = A \bigvee A^c BC\), щоб\(P(A \cup BC) = 0.4 + 0.6 \cdot 0.6 \cdot 0.8 = 0.6880\)
Значно менше арифметичних операцій потрібно в цьому розрахунку.
У великих задачах, або в ситуаціях, коли ймовірності декількох булевих комбінацій повинні бути визначені, може бути бажано обчислити всі мінтермальні ймовірності, а потім використовувати методи мінтерм-вектора, введені раніше для обчислення ймовірностей для різних булевих комбінацій. Як більший приклад, для якого обчислювальна допомога є дуже бажаною, знову розглянемо клас та ймовірності, використані в прикладі 4.2.2, вище.
Приклад\(\PageIndex{9}\)
Розглянемо ще раз незалежний клас {\(E_1, E_2, \cdot\cdot\cdot E_{10}\)} з відповідними ймовірностями [0.13 0.37 0.12 0.56 0.33 0.71 0.22 0.43 0.57 0.31]. Бажаємо розрахуватиІснують\(2^{10} = 1024\) мінімальні ймовірності, які потрібно обчислити. Кожен вимагає множення десяти чисел. Рішення з MATLAB є простим, наступним чином:
>> P = 0.01*[13 37 12 56 33 71 22 43 57 31]; >> minvec10 Vectors are A1 thru A10 and A1c thru A10c They may be renamed, if desired. >> F = (A1|(A3&(A4|A7c)))|(A2&(A5c|(A6&A8)))|(A9&A10c); >> pm = minprob(P); >> PF = F*pm' PF = 0.6636
Виписання виразу для\(F\) є нудним і схильним до помилок. Ми могли б спростити наступним чином:
>> A = A1|(A3&(A4|A7c)); >> B = A2&(A5c|(A6&A8)); >> C = A9&A10c; >> F = A|B|C; % This minterm vector is the same as for F above
Це розкладання проблеми вказує на те, що вона може бути вирішена як низка менших проблем. По-перше, нам потрібні деякі центральні факти про незалежність булевих комбінацій.
Незалежні логічні комбінації
Припустимо, що у нас є логічна комбінація подій у класі {\(A_i: 1 \le i \le n\)} та друга комбінація подій у класі {\(B_j: 1 \le j \le m\)}. Якщо комбінований клас {\(A_i, B_j: 1 \le i \le n, 1 \le j \le m\)} незалежний, ми очікуємо, що комбінації підкласів будуть незалежними. Важливо бачити, що це насправді є наслідком правила продукту, оскільки це ще одне свідчення того, що правило продукту охопило суть інтуїтивного поняття незалежності. У наступному обговоренні ми показуємо істотну структуру, яка забезпечує основу для наступної загальної пропозиції.
Пропозиція. Розглянемо\(n\) окремі підкласи незалежного класу подій. Якщо для кожної\(i\) події\(A_i) is a Boolean (logical) combination of members of the \(i\) -й підклас, то клас {\ (A_1, A_2,\ cdot\ cdot\ cdot, a_n} є незалежним класом.
Перевірка цього далекосяжного результату спирається на мінтермальне розширення і два елементарних факти про неспільних підкласах незалежного класу. Ми констатуємо ці факти і розглядаємо в кожному конкретному випадку приклад, який демонструє істотну структуру. Формулювання загального результату, в кожному конкретному випадку, просто питання ретельного використання позначень.
Клас, кожен з членів якого є мінтерміном, утвореним членами окремого підкласу незалежного класу, сам по собі є незалежним класом.
Приклад\(\PageIndex{10}\)
Розглянемо незалежний клас {\(A_1, A_2, A_3, B_1, B_2, B_3, B_4\)}, з відповідними ймовірностями 0,4, 0,7, 0,3, 0,5, 0,8, 0,3, 0,6. Розглянемо\(M_3\), minterm три для класу {\(A_1, A_2, A_3\)}, і\(N_5\), minterm п'ять для класу {\(B_1\),\(B_2\),\(B_3\),\(B_4\)}. Тоді
\(P(M_3) = P(A_1^c A_2 A_3) = 0.6 \cdot 0.7 \cdot 0.3 = 0.126\)і\(P(N_5) = P(B_1^c B_2 B_3^c B_4) = 0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6 = 0.168\)
Також
\(P(M_3 N_5) = P(A_1^c A_2 A_3 B_1^c B_2 B_3^c B_40 = 0.6 \cdot 0.7 \cdot 0.3 \cdot 0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6\)
\(=(0.6 \cdot 0.7 \cdot 0.3) \cdot (0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6) = P(M_3)P(N_5) = 0.0212\)
Правило продукту показує бажану незалежність.
Знову ж таки, має бути очевидним, що результат тримає будь-яку кількість\(A_i\) і\(B_j\); і його можна розширити на будь-яку кількість різних підкласів незалежного класу.
Припустимо, кожен член класу може бути виражений у вигляді нез'єднаного союзу. Якщо кожен допоміжний клас, утворений шляхом взяття по одному члену з кожного з нероз'єднаних об'єднань, є незалежним класом, то початковий клас незалежний.
Приклад\(\PageIndex{11}\)
Припустимо\(B = B_1 \bigvee B_2\),\(A = A_1 \bigvee A_2 \bigvee A_3\) і, з {\(A_i\),\(A_j\)} незалежним для кожної пари\(i, j\). ПрипустимоМи хочемо показати, що пара {\(A\),\(B\)} є незалежною; тобто правило продукту\(P(AB) = P(A)P(B)\) тримається.
ОБЧИСЛЕННЯ
\(P(A) = P(A_1) + P(A_2) + P(A_3) = 0.3 + 0.4 + 0.1 = 0.8\)і\(P(B) = P(B_1) + P(B_2) = 0.2 + 0.5 = 0.7\)
Зараз
\(AB = (A_1 \bigvee A_2 \bigvee A_3) (B_1 \bigvee B_2) = A_1B_1 \bigvee A_1 B_2 \bigvee A_2 B_1 \bigvee A_2 B_2 \bigvee A_3 B_1 \bigvee A_3 B_2\)
За адитивності та попарної незалежності ми маємо
\(P(AB) = P(A_1) P(B_1) + P(A_1) P(B_2) + P(A_2) P(B_1) + P(A_2)P(B_2) + P(A_3) P(B_1) + P(A_3) P(B_2)\)
\(= 0.3 \cdot 0.2 + 0.3 \cdot 0.5 + 0.4 \cdot 0.2 + 0.4 \cdot 0.5 + 0.1 \cdot 0.2 + 0.1 \cdot 0.5 = 0.56 = P(A) P(B)\)
Правило добутку також може бути встановлено алгебраїчно з виразу for\(P(AB)\), наступним чином:
\(P(AB) = P(A_1)[P(B_1) + P(B_2)] + P(A_2) [P(B_1) + P(B_2)] + P(A_3) [P(B_1) + P(B_2)]\)
\(= [P(A_1) + P(A_2) + P(A_3)][P(B_1) + P(B_2)] = P(A) P(B)\)
Повинно бути зрозуміло, що тільки що проілюстрований візерунок можна розширити на загальний випадок. Якщо
то пара {\(A, B\)} незалежна. Крім того, ми можемо розширити це правило до потрійного {\(A, B, C\)}
і аналогічно для будь-якого кінцевого числа таких комбінацій, так що друга пропозиція тримає.
Почніть з
самостійного класу\(n\) подій. Виберіть\(m\) різні підкласи і сформуйте логічні комбінації для кожного з них. Використання мінтермального розширення для кожної з цих булевих комбінацій та двох лише проілюстрованих пропозицій показує, що клас логічних комбінацій є незалежним.
Для ілюстрації повернемося до Прикладу 4.2.9, який передбачає незалежний клас з десяти подій.
Приклад\(\PageIndex{12}\) A hybrid approach
Розглянемо знову незалежний клас {\(E_1, E_2, \cdot\cdot\cdot, E_{10}\)} з відповідними ймовірностями {0,13 0,37 0,12 0,56 0,33 0,71 0,22 0,43 0,57 0,31}. Бажаємо розрахувати\(P(F) = P(E_1 \cup E_3 (E_4 \cup E_7^c) \cup E_2 (E_5^c \cup E_6 E_8) \cup E_9 E_10^c)\)
У попередньому рішенні ми використовуємо minprob, щоб обчислити\(2^{10}=1024\) мінтерми для всіх десяти\(E_i\) і визначити мінтерм-вектор для\(F\). Як ми відзначаємо в почерговому розширенні\(F\),
Ми можемо розраховувати безпосередньо\(P(C) = 0.57 \cdot 0.69 = 0.3933\). Тепер\(A\) це логічна комбінація {\(E_1, E_3, E_4, E_7\)} і B є комбінацією {\(E_2, E_5, E_6 E_8\)}. За результатом незалежності булевих комбінацій клас {\(A, B, C\)} є незалежним. Використовуємо m-процедури для розрахунку\(P(A)\) і\(P(B)\). Потім ми маємо справу з незалежним класом {\(A, B, C\)} для отримання ймовірності\(F\).
>> p = 0.01*[13 37 12 56 33 71 22 43 57 31];
>> pa = p([1 3 4 7]); % Selection of probabilities for A
>> pb = p([2 5 6 8]); % Selection of probabilities for B
>> pma = minprob(pa); % Minterm probabilities for calculating P(A)
>> pmb = minprob(pb); % Minterm probabilities for calculating P(B)
>> minvec4;
>> a = A|(B&(C|Dc)); % A corresponds to E1, B to E3, C to E4, D to E7
>> PA = a*pma'
PA = 0.2243
>> b = A&(Bc|(C&D)); % A corresponds to E2, B to E5, C to E6, D to E8
>> PB = b*pmb'
PB = 0.2852
>> PC = p(9)*(1 - p(10))
PC = 0.3933
>> pm = minprob([PA PB PC]);
>> minvec3 % The problem becomes a three variable problem
>> F = A|B|C; % with {A,B,C} an independent class
>> PF = F*pm'
PF = 0.6636 % Agrees with the result of Example 4.2.7