1.3: Тлумачення

Що таке ймовірність?

Формальна система ймовірностей - це модель, корисність якої може бути встановлена лише шляхом вивчення її структури та визначення того, чи можна адекватно представити закономірності невизначеності та ймовірності в будь-якій практичній ситуації. За винятком певної події та неможливої події, модель не говорить нам, як призначити ймовірність будь-якої події. Формальна система узгоджується з багатьма завданнями ймовірності, так само, як поняття маси узгоджується з багатьма різними масовими призначеннями множин у базовому просторі.

Визначальні властивості (P1), (P2), (P3) та похідні властивості забезпечують правила узгодженості для присвоєння ймовірностей. Не можна призначити негативні ймовірності або ймовірності більше одиниці. Впевненій події присвоюється ймовірність один. Якщо дві або більше подій є взаємовиключними, загальна ймовірність, присвоєна союзу, повинна дорівнювати сумі ймовірностей окремих подій. Допускається будь-яке призначення ймовірності, що відповідає цим умовам.

Можна не знати привласнення ймовірності кожної події. Подібно до того, як визначальні умови ставлять обмеження на допустимі призначення ймовірності, вони також забезпечують важливу структуру. Типова прикладна задача забезпечує ймовірності членів класу подій (можливо, лише декількох), з яких можна визначити ймовірності інших подій, що цікавлять. Розглянемо важливий клас таких задач в наступному розділі.

Існує безліч точок зору щодо того, як слід інтерпретувати ймовірність. Вони впливають на спосіб, в якому ймовірності призначаються (або припускаються). Одна важлива дихотомія серед практикуючих.

• Одна група вважає ймовірність об'єктивною в тому сенсі, що це щось притаманне природі речей. Його слід виявити, якщо це можливо, шляхом аналізу та експерименту. Чи можемо ми це визначити чи ні, «воно є».
• Інша група наполягає на тому, що ймовірність - це стан розуму людини, яка робить оцінку ймовірності. З цієї точки зору закони ймовірності просто нав'язують раціональну послідовність способу присвоєння ймовірностей подіям. Були зроблені різні спроби знайти об'єктивні способи вимірювання сили свого переконання або ступеня впевненості в тому, що подія відбудеться. Імовірність\(P(A)\) виражає ступінь впевненості, яку відчувають, що відбудеться подія А. Один з підходів до характеристики ступеня визначеності індивіда полягає в тому, щоб прирівняти його оцінку до суми, яку він готовий заплатити, щоб грати в гру, яка повертає одну одиницю грошей, якщо A відбувається, для виграшу\((1 - a)\), і повертає нуль, якщо A не\(P(A)\) відбуваються, для виграшу\(-a\). За цим формулюванням стоїть поняття чесної гри, в якій «очікуваний» або «середній» виграш дорівнює нулю.

Рання робота над ймовірністю почалася з вивчення відносних частот виникнення події під час повторних, але незалежних випробувань. Ця ідея настільки вбудована в інтуїтивну думку про ймовірність, що деякі імовірністи наполягали на тому, що вона повинна бути вбудована у визначення ймовірності. Цей підхід не був повністю успішним математично і не привернув багато наступних серед теоретичних або прикладних імовірністів. У моделі, яку ми приймаємо, існує фундаментальна гранична теорема, відома як теорема Бореля, яку можна інтерпретувати: «якщо випробування виконується велику кількість разів незалежним чином, частка разів, що\(A\) відбувається подія, наближається як межа значення \(P(A)\). Встановлення цього результату (чого ми не робимо в цьому лікуванні) забезпечує офіційну перевірку інтуїтивного поняття, яке лежить за ранніми спробами сформулювати ймовірності. Завзяті гравці відзначали багаторічні статистичні закономірності і шукали пояснень у своїх математично обдарованих друзів. З цієї точки зору ймовірність має сенс тільки в повторюваних ситуаціях. Ті, хто дотримується цієї точки зору, зазвичай припускають об'єктивний погляд на ймовірність. Це число, яке визначається природою реальності, яке необхідно виявити шляхом повторного експерименту.

Існує багато застосувань ймовірності, в яких відносна частота точки зору нездійсненна. Приклади включають прогнози погоди, результат гри або скачки, виконання індивіда на певній роботі, успіх новоствореного комп'ютера. Це унікальні, неповторювані випробування. Як має популярний вислів, «Ви ходите навколо лише один раз». Іноді ймовірності в цих ситуаціях можуть бути досить суб'єктивними. Насправді ті, хто приймає суб'єктивний погляд, схильні думати з точки зору таких проблем, тоді як ті, хто приймає об'єктивний погляд, зазвичай підкреслюють частотну інтерпретацію.

Суб'єктивна ймовірність і футбольний матч

Імовірність того, що улюблена футбольна команда виграє наступну гру Superbowl, цілком може бути лише суб'єктивною ймовірністю беттора. Це, звичайно, не ймовірність, яку можна визначити за допомогою великої кількості повторних випробувань. Гра проводиться лише один раз. Однак суб'єктивна оцінка ймовірностей може базуватися на інтимних знаннях відносних сильних і слабких сторін залучених команд, а також таких факторів, як погода, травми та досвід. Може бути значна об'єктивна основа для суб'єктивного присвоєння ймовірності. Насправді в суб'єктивній оцінці часто присутній прихований «частотний» елемент. Існує оцінка (можливо, нереалізована), що в подібних ситуаціях частоти, як правило, збігаються з суб'єктивно призначеним значенням.

Імовірність дощу

Новинні випуски часто повідомляють, що ймовірність дощу становить 20 відсотків або 60 відсотків або якась інша цифра. Тут є кілька складнощів.

• Для використання формальної математичної моделі повинна бути точність у визначенні події. Подія або відбувається, або не відбувається. Як ми визначаємо, пішов дощ чи ні? Чи повинна бути вимірна сума? Куди повинен бути зарахований цей дощ? За який часовий проміжок? Навіть якщо є домовленість щодо площі, суми та часового періоду, залишається неоднозначність: не можна з логічною впевненістю сказати, що подія все-таки відбулася або вона не відбулася. Проте в цій та інших подібних ситуаціях використання поняття події може бути корисним, навіть якщо опис не є остаточним. Зазвичай існує достатньо практичної згоди, щоб концепція була корисною.
• Що означає 30-відсоткова ймовірність дощу? Чи означає це, що якщо прогноз буде правильним, 30 відсотків зазначеної площі отримають дощ (в узгодженій кількості) протягом зазначеного періоду часу? Або це означає, що 30 відсотків випадків, коли робиться такий прогноз, протягом зазначеного періоду часу в районі будуть значні опади? Знову ж таки, остання альтернатива цілком може приховувати частотну інтерпретацію. Чи означає твердження, що йде дощ 30 відсотків випадків, коли умови схожі на нинішні умови?

Незалежно від трактування, існує певна неоднозначність щодо події та того, чи відбулося воно. І є певні труднощі з знанням того, як інтерпретувати цифру ймовірності. Хоча точне значення 30-відсоткової ймовірності дощу може бути важко визначити, як правило, корисно знати, чи призводять умови до 20 відсотків або 30 відсотків або 40 відсотків. І немає сумнівів, що, оскільки технологія прогнозування погоди та методологія продовжують вдосконалюватися, оцінки ймовірності погоди стануть все більш корисними.

Інший поширений тип ймовірнісної ситуації передбачає визначення розподілу якоїсь характеристики по населенню - як правило, шляхом опитування. Ці дані використовуються для відповіді на питання: Яка ймовірність (ймовірність) того, що член населення, обраний «навмання» (тобто на однаково імовірній основі) матиме певну характеристику?

Емпірична ймовірність на основі даних опитування

Опитування задає два питання 300 студентів: Ви живете в кампусі? Ви задоволені відпочинковими закладами в студентському центрі? Відповіді на останнє питання були класифіковані «розумно задоволені», «незадоволені» або «немає певної думки». \(C\)Дозволяти бути подією «на кампусі;»\(O\) бути подією «поза кампусом;»\(S\) бути подією «розумно задоволені;»\(U\) бути подією «незадоволені;» і\(N\) бути подією «немає певної думки». Дані наведені в наступній таблиці.

Дані опитування

	S	У	П
C	127	31	42
O	46	43	11

Якщо особа вибирається на однаково імовірній основі з цієї групи 300, ймовірність будь-якої з подій приймається відносною частотою респондентів у кожній категорії, що відповідає тій чи іншій події. Є 200 на кампусі членів в населенні, так\(P(C) = 200/300\) і\(P(O) = 100/300\). Імовірність того, що студент обраний знаходиться на кампусі і задоволений приймається бути\(P(CS) = 127/300\). Імовірність студент або на кампусі і задоволений або поза кампусом і не задоволений

\(P(CS \bigvee OU) = P(CS) + P(OU) = 127/300 + 43/300 = 170/300\)

Якщо є підстави вважати, що вибіркова популяція є репрезентативною для всього студентського тіла, то ті ж ймовірності будуть застосовані до будь-якого студента, обраного навмання з усього студентського тіла.

Пощастило, що нам не потрібно оголошувати жодної позиції, щоб бути «правильною» точкою зору та інтерпретацією. Формальна модель узгоджується з будь-якою з викладених поглядів. Ми вільні в будь-якій ситуації зробити інтерпретацію найбільш значущою і природною для проблеми під рукою. Не потрібно вписувати всі проблеми в одну концептуальну форму; також не потрібно змінювати математичну модель кожного разу, коли інша точка зору здається доречною.

Ймовірність і коефіцієнти

Часто нам зручно працювати з співвідношенням ймовірностей. Якщо\(A\) і\(B\) є подіями з позитивною ймовірністю, шанси на\(A\) користь\(B\) - це коефіцієнт ймовірності\(P(A)P(B)\). Якщо не вказано інше,\(B\) приймається,\(A^c\) і ми говоримо про шанси, що сприяють\(A\)

\(O(A) = \dfrac{P(A)}{P(A^c)} = \dfrac{P(A)}{1 - P(A)}\)

Цей вираз може бути розв'язаний алгебраїчно, щоб визначити ймовірність з коефіцієнтів

\(P(A) = \dfrac{O(A)}{1 + O(A)}\)

Зокрема, якщо\(O(A) = a/b\) тоді\(P(A) = \dfrac{a/b}{1+a/b} = \dfrac{a}{a+b}\).

\(O(A) = 0.7/0.3 = 7/3\). Якщо шанси на користь\(A\) 5/3, то\(P(A) = 5/(5 + 3) = 5/8\).

Розділи та логічні комбінації подій

Зліченна властивість адитивності (P3) ставить премію за відповідне поділ подій.

Визначення

Розділ - це взаємовиключний клас

\({A_i : i \in J}\)такий, що\(\Omega = \bigvee_{i \in J} A_i\)

Розділ події\(A\) - це взаємовиключний клас

\({A_i : i \in J}\)такий, що\(A = \bigvee_{i \in J} A_i\)

Зауваження.

• Розділ - це взаємовиключний клас подій, таких, що на кожному випробуванні має відбуватися одне (і тільки одне).
• Розділ події\(A\) - це взаємовиключний клас подій, таких, що\(A\) відбувається, якщо один (і тільки один)\(A_i\) відбувається.
• Розділ (без класифікатора) приймається як розділ певної події\(\Omega\).
• Якщо клас\({B_i : i \in J}\) взаємовиключний і\(A \subset B = \bigvee_{i \in J} B_i\), то клас\({AB_i : i \in J}\) є розділом\(A\) і\(A = \bigvee_{i \in J} AB_i\).

Ми можемо почати з послідовності\({A_1: 1 \le i}\) і визначити взаємовиключну (непоєднувану) послідовність\({B_1: 1 \le i}\) наступним чином:

\(B_1 = A_1\), і для будь-якого\(i > 1\),\(B_i = A_i A_{1}^{c} A_{2}^{c} \cdot\cdot\cdot A_{i - 1}^{c}\)

Таким чином\(B_i\), кожен є сукупністю цих елементів\(A_i\) не в жодному з попередніх членів послідовності.

Це уявлення використовується для того, щоб показати, що субадитивність (P9) випливає з підрахункової адитивності та властивості (P6). Починаючи з кожного\(B_i \subset A_i\), по (Р6)\(P(B_i) \le P(A_i)\). Зараз

\(P(\bigcup_{i = 1}^{\infty} A_i) = P(\bigvee_{i = 1}^{\infty} B_i) = \sum_{i = 1}^{\infty} P(B_i) \le \sum_{i = 1}^{\infty} P(A_i)\)

Представлення союзу як незв'язаного союзу вказує на важливу стратегію у вирішенні ймовірнісних проблем. Якщо подія може бути виражена як зліченний неспільний союз подій, кожна з ймовірностей якого відома, то ймовірність комбінації - це сума окремих ймовірностей. У модулі про розділи та Мінтерми ми показуємо, що будь-яка логічна комбінація скінченного класу подій може бути виражена у вигляді незв'язкового об'єднання таким чином, що часто сприяє систематичному визначенню ймовірностей.

Функція індикатора

Одним з найбільш корисних інструментів для роботи з безліччю комбінацій (а значить і з комбінаціями подій) є \(I_E\)індикаторна функція для набору\(E \subset \Omega\). Визначається він дуже просто наступним чином:

\(I_E (\omega) = \begin{cases}1 & \text{for } \omega \in E \\ 0 & \text{for } \omega \in E^c \end{cases}\)

Зауваження. Функції індикаторів можуть бути визначені на будь-якому домені. Ми маємо привід у різних випадках визначити їх на дійсній лінії та на вищих розмірних евклідових просторах. Наприклад, якщо\(M\) інтервал [\(a,b\)] на дійсному рядку, то\(I_M(t) = 1\) для кожного\(t\) в інтервалі (а в іншому випадку дорівнює нулю). Таким чином, у нас є step-функція з одиничним значенням протягом інтервалу\(M\). У абстрактному базовому просторі\(\Omega\) ми не можемо так легко намалювати графік. Однак при поданні множин на діаграмі Венна можна дати схематичне зображення, як на малюнку 1.3.1.

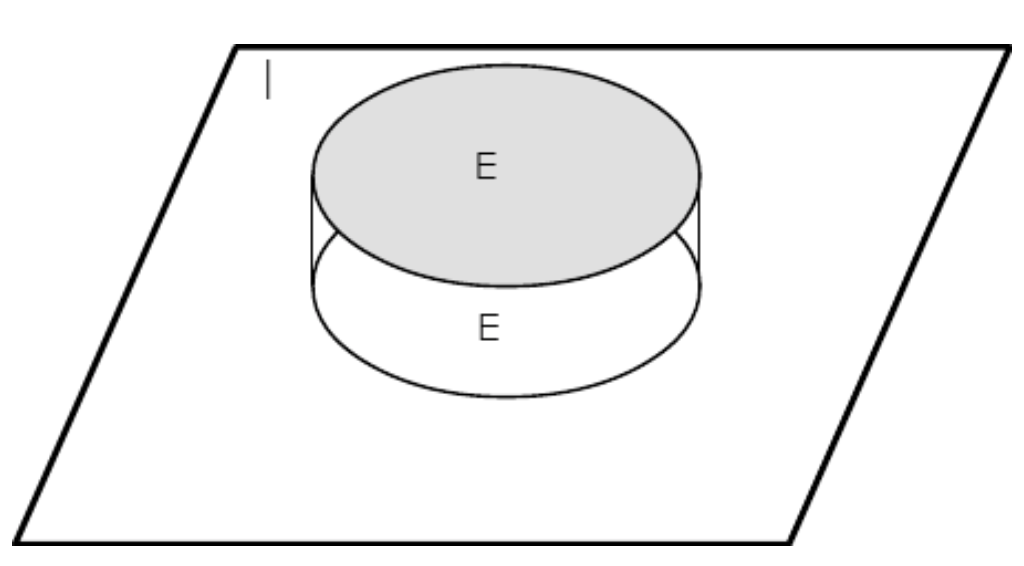
Малюнок 1.3.1. Представлення індикаторної функції\(I_E\) для події\(E\).

Значна частина корисності індикаторної функції походить від наступних властивостей.

(IF1):\(I_A \le I_B\) іфф\(A \subset B\). Якщо\(I_A \le I_B\), то\(\omega \in A\) має на увазі\(I_A (\omega) = I_B (\omega) = 1\), так\(\omega \in B\), то\(I_A (\omega) = 1\) має\(\omega \in A\) на увазі\(\omega \in B\) увазі\(I_B (\omega) = 1\).
(IF2):\(I_A = I_B\) вимкнено\(A = B\)

\(A = B\)вимкніть обидва\(A \subset B\) і\(B \subset A\) вимкніть\(I_A \le I_B\) і\(I_B \le I_A\) вимкніть\(I_A = I_B\)

(IF3):\(I_{A^c} = 1 - I_A\) Це випливає з факту\(I_{A^c} (\omega) = 1\) iff\(I_A (\omega) = 0\).
(IF4):\(I_{AB} = I_A I_B = \text{min } {I_A, I_B}\) (поширюється на будь-який клас) Елемент ω належить до перетину, якщо він належить усім, якщо індикаторна функція для кожної події одна, якщо добуток індикаторних функцій один.
(IF5):\(I_{A \cup B} = I_A + I_B - I_A I_B = \text{min }{I_A, I_B}\) (правило максимуму поширюється на будь-який клас) Правило максимуму випливає з того факту, що\(\omega\) знаходиться в об'єднанні, якщо воно є в будь-якій одній або декількох подіях в об'єднанні, якщо будь-яка одна або кілька окремих індикаторних функцій має значення один iff максимальний один. Правило суми для двох подій встановлюється правилом і властивостями DeMorgan (IF2), (IF3) і (IF4).

\(I_{A \cup B} = 1 - I_{A^c B^c} = 1 - [1 - I_A][1 - I_B] = 1 - 1 + I_B + I_A - I_A I_B\)

(IF6): Якщо пара\({A, B}\) нез'єднана,\(I_{A \bigvee B} = I_A+ I_B\) (поширюється на будь-який неспільний клас)

Наступний приклад ілюструє використання індикаторних функцій при встановленні взаємозв'язків між множинними комбінаціями. Інші способи використання та методи встановлюються в модулі «Розділи» та «Мінтермс».

Функції індикатора і набори комбінацій

Припустимо,\({A_i : 1 \le i \le n}\) це перегородка.

Якщо\(B = \bigvee_{i = 1}^{n} A_i C_i\), то\(B^c = \bigvee_{i = 1}^{n} A_i C_{i}^{c}\)

Доказ

Використовуючи властивості індикаторної функції, встановленої вище, ми маємо

\(I_B = \sum_{i = 1}^{n} I_{A_i} I_{C_i}\)

Зверніть увагу, що оскільки\(A_i\) форма розділу, у нас є\(\sum_{i = 1}^{n} I_{A_i} = 1\), так що функція індикатора для взаємодоповнюючої події

\(I_{B^c} = 1 - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} I_{A_i} - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} [1 - I_{C_i}] = \sum_{i = 1}^{n} I_{A_i} I_{C_{i}^{c}}\)

Остання сума - індикаторна функція для\(\bigvee_{i = 1}^{n} A_i C_{i}^{c}\)

Технічний коментар до класу подій

Клас подій відіграє центральну роль в інтуїтивному тлі, застосуванні та формальній математичній структурі. Події були змодельовані як підмножини базового простору всіх можливих результатів випробування або експерименту. У випадку кінцевого числа результатів, будь-яка підмножина може бути прийнята як подія. У загальній теорії, що передбачає нескінченні можливості, існують деякі технічні математичні причини обмеження класу підмножин, що розглядаються як події. Практичні потреби такі:

1. Якщо\(A\) це подія, її додатковий набір також повинен бути подією.
2. Якщо\({A_i : i \in J}\) є кінцевим або зліченним класом подій, об'єднання і перетин членів класу повинні бути подіями.

Простий аргумент, заснований на правилах DeMorgan, показує, що якщо клас містить доповнення всіх його множин і обчислюваних спілок, то він містить лічильні перетину. Так само, якщо він містить доповнення всіх своїх наборів та лічильних перетинів, то він містить лічильні союзи. Клас множин, закритих під доповненнями та підрахунковими союзами, відомий як сигма-алгебра множин. У формальному, теоретично-вимірювальному лікуванні основним припущенням є те, що клас подій - це сигма-алгебра, а міра ймовірності присвоює членам цього класу ймовірності. Такий клас настільки загальний, що для встановлення того факту, що такий клас містить не всі підмножини, потрібні дуже складні аргументи. Але саме тому, що клас настільки загальний і інклюзивний в звичайних додатках, нам не потрібно турбуватися про те, які множини допустимі як події.

Першочерговим завданням при формулюванні проблеми ймовірності є виявлення відповідних подій і взаємозв'язків між ними. Теоретичне лікування показує, що ми можемо працювати з великою свободою у формуванні подій, із запевненням, що в більшості програм набір, створений таким чином, є математично дійсною подією. Так зване питання вимірюваності вступає в дію лише при роботі з випадковими процесами з безперервними параметрами. Навіть там, за розумними припущеннями, вироблені набори будуть подіями.