1.2: Системи ймовірностей

Міри ймовірності

У модулі «Імовірність» введено поняття базового простору ωΩ всіх можливих результатів випробування або експерименту, подій як підмножин базового простору, визначеного відповідними характеристиками результатів, і логічні або булеві комбінації подій (об'єднань, перетинів і доповнює), що відповідають логічним поєднанням визначальних характеристик.

Виникнення або невиникнення події визначається ознаками або ознаками результату, що спостерігаються на дослідженні. Виконання судового розгляду візуалізується як вибір результату з базового набору. Подія відбувається щоразу, коли вибраний результат є членом підмножини, що представляє подію. Як описано до цих пір, процес відбору може бути досить обдуманим, з встановленим результатом, або він може включати невизначеності, пов'язані з «випадковістю». Імовірність входить в картину тільки в останній ситуації. Перед проведенням судового розгляду існує невизначеність щодо того, яка з цих прихованих можливостей буде реалізована. Імовірність традиційно - це номер, присвоєний події, що вказує на ймовірність виникнення цієї події на будь-якому судовому розгляді.

Почнемо з розгляду класичної моделі, яка вперше успішно сформулювала ймовірнісні ідеї в математичній формі. Для його опису ми використовуємо сучасну термінологію та позначення.

Класична ймовірність

1. Основний простір\(\Omega\) складається з скінченного числа N можливих результатів.
   
   -Є тридцять шість можливих результатів кидання двох кубиків.
   -Є\(C(52,5) = \dfrac{52!}{5! 47!} = 2598960\) різні руки з п'яти карт (порядок не важливий).
   -Є\(2^5 = 32\) результати (послідовності голів або хвостів) гортання п'яти монет.
2. Кожному можливому результату присвоюється ймовірність 1/\(N\)
3. Якщо подія (підмножина)\(A\) має\(N_A\) елементи, то ймовірність присвоєної події\(A\) дорівнює

\(P(A) = N_A /N\)(Тобто, фракція сприятлива для\(A\))

При такому визначенні ймовірності кожній події\(A\) присвоюється унікальна ймовірність, яка може бути визначена підрахунком\(N_A\), кількість елементів в\(A\) (класичною мовою кількість результатів, «сприятливих» до події) і\(N\) загальна кількість можливих результатів в вірна подія\(\Omega\).

Ймовірності для рук карт

Розглянемо експеримент по витягуванню руки з п'яти карт зі звичайної колоди з 52 гральних карт. Кількість результатів, як зазначалося вище, становить\(N = C(52,5) = 2598960 N = C(52,5) = 2598960\). Яка ймовірність розіграшу руки рівно двома тузами? Яка ймовірність розіграшу руки з двома і більше тузами? Яка ймовірність не більше одного туза?

Рішення

\(A\)Дозволяти подією рівно двох тузів,\(B\) бути подією рівно трьох тузів, і\(C\) бути подією рівно чотирьох тузів. У першій задачі ми повинні порахувати\(N_A\) кількість способів малювання руки двома тузами. Ми вибираємо два тузи з чотирьох, а інші три карти вибираємо з 48 без тузів. Таким чином

\(N_A = C(4, 2) C(48,3) = 103776\), щоб\(P(A) = \dfrac{N_A}{N} = \dfrac{103776}{2598960} \approx 0.0399\)

Є два або більше тузів, якщо їх рівно два або рівно три або рівно чотири. Таким чином, подія\(D\) двох або більше є\(D = A \bigvee B \bigvee C\), оскільки\(A, B, C\) є взаємовиключними,

\(N_D = N_A + N_b + N_c = C(4, 2) C(48, 3) + C(4, 3) C(48, 2) + C(4, 4) C(48, 1) = 103776 + 4512 + 48 = 108336\)

так що\(P(D) \approx 0.0417\). Існує один туз або жоден, якщо немає двох або більше тузів. Ми таким чином хочемо\(P(D^c)\). Тепер число в\(D_c\) - це число не в\(D\) якому є\(N - N_D\), так що

\(P(D^c) = \dfrac{N - N_D}{N} = 1 - \dfrac{N_D}{N} = 1 - P(D) = 0.9583\)

Цей приклад ілюструє кілька важливих властивостей класичної ймовірності.

\(P(A) = N_A / N\)є невід'ємною величиною.
\(P(\Omega) = N/N = 1\)
Якщо\(A, B, C\) взаємовиключні, то число в нероз'єднаному союзі - це сума чисел в окремих подіях, так що

\(P(A \bigvee B \bigvee C) = P(A) + P(B) + P(C)\)

Можна виділити кілька інших елементарних властивостей класичної ймовірності. Виявляється, їх можна вивести з цих трьох. Хоча класична модель дуже корисна, і розроблена обширна теорія, вона насправді не є задовільною для багатьох застосувань (наприклад, проблема зв'язку). Ми шукаємо більш загальну модель, яка включає класичну ймовірність як окремий випадок і, таким чином, є її продовженням. Ми приймаємо модель Колмогорова (введена російським математиком А.Н. Колмогоровим), яка надзвичайно успішним чином захоплює основні ідеї. Звичайно, жодна модель ніколи не буває повністю успішною. Реальність завжди, здається, уникає наших логічних мереж.

Модель Колмогорова ґрунтується на теорії абстрактних мір. Повна експлікація вимагає рівня математичної складності, неприйнятного для такого лікування, як це. Але більшість понять і багато результатів елементарні і легко вхоплюються. І багато технічних математичних міркувань не важливі для додатків на рівні цього вступного лікування і можуть бути ігноровані. Ми запозичуємо з теорії мір кілька ключових фактів, які є або дуже правдоподібними, або які можна зрозуміти на практичному рівні. Це дозволяє нам використовувати дуже потужну математичну систему для представлення практичних проблем таким чином, що призводить як до розуміння, так і до корисних стратегій вирішення.

Наш підхід полягає в тому, щоб почати з поняття про події як множини, введені вище, а потім ввести ймовірність як число, присвоєне подіям за певних умов, які стають остаточними властивостями. Поступово ми впроваджуємо та використовуємо додаткові поняття, щоб поступово будувати потужну та корисну дисципліну. Основні необхідні властивості - це лише ті, що проілюстровані в прикладі для класичного випадку.

Визначення

Система ймовірностей складається з\(\Omega\) базового набору елементарних результатів випробування або експерименту, класу подій як підмножин базового простору та міри ймовірності,\(P(\cdot)\) яка призначає значення подіям відповідно до наступних правил:

(P1): Для будь-якої події\(A\) ймовірність\(P(A) \ge 0\).
(P2): Імовірність певної події\(P(\Omega) = 1\).
(P3): Зліченна адитивність. Якщо\({A_i : 1 \in J}\) є взаємовиключним, зліченним класом подій, то ймовірність незв'язкового союзу - це сума індивідуальних ймовірностей.

Необхідність взаємної винятковості (розмежованості) проілюстровано на прикладі. Якби множини не були розмежованими, ймовірність була б зарахована більше одного разу в сумі. Імовірність, як визначено, є абстрактною - просто номер, присвоєний кожному набору, що представляє подію. Але ми можемо дати йому інтерпретацію, яка допомагає візуалізувати різні закономірності та стосунки, що зустрічаються. Ми можемо думати про ймовірність як масу, призначену події. Загальна одинична маса віднесена до базового набору\(\Omega\). Властивість адитивності для нез'єднаних множин робить масову інтерпретацію послідовною. Ми можемо використовувати це тлумачення як точне уявлення. Неодноразово ми посилаємося на масу ймовірностей, присвоєну заданому множині. Маса пропорційна вазі, тому іноді ми говоримо неофіційно про вагу, а не про масу. Тепер масове призначення з трьома властивостями здається не дуже перспективним початком. Але незабаром ми розширимо цей рудиментарний список властивостей. Ми використовуємо масову інтерпретацію, щоб допомогти візуалізувати властивості, але в першу чергу стурбовані інтерпретацією їх з точки зору ймовірності.

(Р4):\(P(A^c) = 1 - P(A)\). З адитивності випливає і той факт, що

\(1 = P(\Omega) = P(A \bigvee A^c) = P(A) + P(A^c)\)

(Р5):\(P(\emptyset) = 0\). Порожній набір представляє неможливу подію. Він не має членів, отже, не може відбуватися. Здається розумним, що їй слід призначити нульову ймовірність (масу). Так як\(\emptyset = \Omega^c\), це логічно випливає з Р (4) і (Р2).

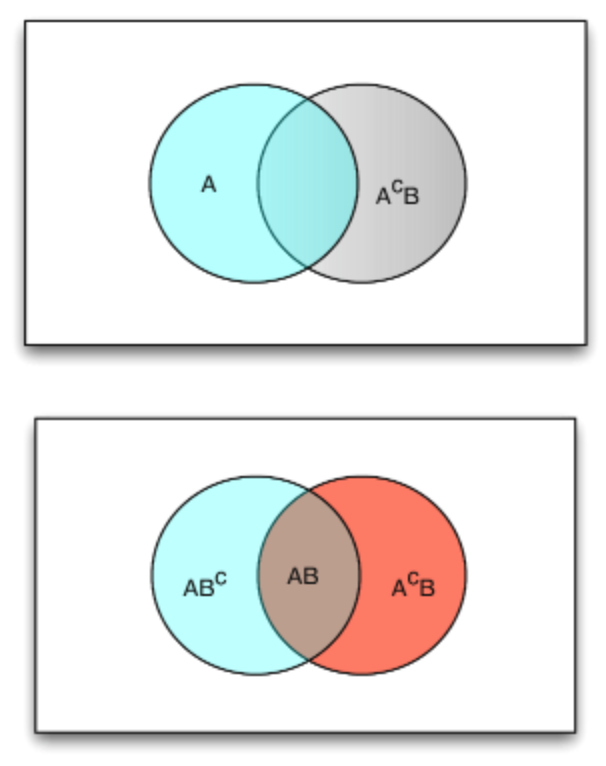
Малюнок 1.2.1: Перегородки об'єднання\(A \cup B\)

(P6): Якщо\(A \subset B\), то\(P(A) \le P(B)\). З точки зору маси, кожна точка також в\(A\)\(B\), так що\(B\) повинна мати принаймні стільки ж маси, скільки\(A\). Тепер відносини\(A \subset B\) означають, що якщо\(A\) відбувається,\(B\) повинні також. Отже\(B\), принаймні так само ймовірно, що відбудеться, як\(A\). З чисто формальної точки зору ми маємо

\(B = A \bigvee A^c B\)так що\(P(B) = P(A) + P(A^c B) \ge P(A)\) з тих пір\(P(A^c B) \ge 0\)

(Р7):\(P(A \cup B) = P(A) + P(A^c B) = P(B) + P(AB^c) = P(AB^c) + P(AB) + P(A^cB)\)

\(= P(A) + P(B) - P(AB)\)

Перші три вирази випливають з адитивності та розбиття\(A \cup B\) наступним чином (див. Рис.

\(A \cup B = A \bigvee A^c B = B \bigvee AB^c = AB^c \bigvee AB \bigvee A^c B\)

Якщо додати перші два вирази і відняти третє, то отримаємо останній вираз. Що стосується маси ймовірності, перший вираз говорить, що ймовірність в -\(A \cup B\) це маса ймовірності\(A\) плюс додаткова маса ймовірності в тій частині\(B\), в якій немає\(A\). Аналогічне тлумачення тримає і для другого виразу. Третя - ймовірність в загальній частині плюс додатковий\(A\) і додатковий в\(B\). Якщо ми додаємо масу в\(A\) і\(B\) ми порахували масу в загальній частині двічі. Останній вираз показує, що ми виправляємо це, забираючи зайву загальну масу.

(P8): Якщо\({B_i : i \in J}\) є лічильним, непоєднуваним класом і\(A\) міститься в союзі, то

\(A = \bigvee_{i \in J} AB_i\)щоб\(P(A) = \sum_{i \in J} P(AB_i)\)

(P9): Субадитивність. Якщо\(A = \bigcup_{i = 1}^{\infty} A_i\), то\(P(A) \le \sum_{i = 1}^{\infty} P(A_i)\). Це випливає з рахункової адитивності, властивості (Р6) та факту

(Перегородки)

\(A = \bigcup_{i = 1}^{\infty} A_i = \bigvee_{i = 1}^{\infty} B_i\), де\(B_i = A_i A_1^c A_2^c \cdot\cdot\cdot A_{i - 1}^c \subset A_i\)

Сюди входить як окремий випадок об'єднання кінцевої кількості подій.

Деякі з цих властивостей, такі як (P4), (P5) та (P6), настільки елементарні, що, здається, їх слід включити до визначального твердження. Це не було б неправильно, але було б неефективно. Якщо у нас є присвоєння чисел подіям, нам потрібно лише встановити (P1), (P2) та (P3), щоб мати можливість стверджувати, що присвоєння є мірою ймовірності. А інші властивості слідують як логічні наслідки.

Гнучкість за ціною

Виходячи за рамки класичної моделі, ми отримали велику гнучкість і адаптивність моделі. Він може бути використаний для систем, в яких кількість результатів нескінченна (зліченно або незліченно). Він не вимагає рівномірного розподілу маси ймовірності між результатами. Наприклад, проблема кісток може бути вирішена безпосередньо шляхом присвоєння відповідних ймовірностей різним числом загальних плям, від 2 до 12. Як ми бачимо при лікуванні умовної ймовірності, ми робимо нові присвоєння ймовірностей (тобто вводять нові міри ймовірності) при отриманні часткової інформації про результат.

Але ця свобода виходить за ціною. У класичному випадку чітко визначено значення ймовірності, яке буде присвоєно події (хоча виконати необхідний підрахунок може бути дуже складно). У загальному випадку ми повинні вдатися до досвіду, структури досліджуваної системи, експерименту або статистичних досліджень, щоб призначити ймовірності.

Існування невизначеності через «випадковість» або «випадковість» не обов'язково означає, що акт виконання судового розгляду є випадковим. Судовий розгляд може бути досить ретельно спланований; непередбачені обставини можуть бути наслідком факторів, що не залежать від експериментатора або знань. Механізм випадковості (тобто джерело невизначеності) може залежати від характеру фактичного процесу або системи, що спостерігається. Наприклад, при прийнятті погодинного профілю температури в даний день на метеостанції основні варіації пов'язані не з експериментальною помилкою, а скоріше з невідомими факторами, які сходяться, щоб забезпечити конкретний характер погоди. У разі невиправленої цифрової помилки передачі причина невизначеності криється в тонкощах механізмів корекції і збуреннях, що створюються дуже складним середовищем. Пацієнт в клініці може бути обраний самостійно. Перед його появою і результатом тесту лікар може не знати, у якого пацієнта, з яким станом з'явиться. У кожному випадку, з точки зору експериментатора, причину просто приписують «випадковість». Незалежно від того, чи сприймає це як «акт богів» або просто результат конфігурації фізичних чи поведінкових причин занадто складних для аналізу, ситуація є невизначеністю перед судом, про який результат представить себе.

Якби була повна невизначеність, ситуація була б хаотичною. Але зазвичай це не так. Хоча існує надзвичайно велика кількість можливих погодинних температурних профілів, значна підмножина з них має дуже мало ймовірності виникнення. Наприклад, профілі, в яких послідовні годинні температури чергуються між дуже високими, то дуже низькими значеннями протягом дня, становлять малоймовірну підмножину (подію). Зазвичай очікують тенденції температури протягом 24-годинного періоду. Хоча дорожній інженер не знає точно, скільки транспортних засобів буде спостерігатися в даний період часу, досвід дає деяке уявлення про те, який діапазон значень очікувати. Хоча існує невизначеність щодо того, який пацієнт, з якими симптомами з'являться в клініці, лікар, безумовно, знає приблизно, яка частка пацієнтів клініки має дане захворювання. У азартній грі, проаналізованій на «однаково ймовірні» результати, припущення рівної ймовірності ґрунтується на знанні симетрій та структурних закономірностей у механізмі, за допомогою якого здійснюється гра. І кількість результатів, пов'язаних з даною подією, відомо, або може бути визначено.

У кожному конкретному випадку існує певна основа статистичних даних про минулий досвід або знання структури, регулярності та симетрії в спостережуваної системі, що дозволяє привласнювати ймовірності виникнення різних подій. Саме ця здатність привласнювати ймовірності різним подіям характеризує прикладну ймовірність. Однак визначена, ймовірність - це номер, присвоєний подіям, щоб вказати на їх ймовірність виникнення. Призначення повинні відповідати визначальним властивостям (P1), (P2), (P3) разом з похідними властивостями (P4) через (P9) (плюс інші, які також можуть бути отримані з них). Оскільки ймовірності не «вбудовані», як у класичному випадку, основна роль теорії ймовірностей полягає у отриманні інших ймовірностей із набору заданих ймовірностей.