3.4: Обмеження довіри

Цілі навчання

• Межі довіри говорять вам, наскільки точною буде ваша оцінка середнього значення.

Вступ

Після того, як ви розрахували середнє значення набору спостережень, вам слід вказати, наскільки близькою буде ваша оцінка до параметричного («істинного») середнього. Один із способів зробити це - з обмеженнями впевненості. Межі довіри - це числа у верхньому та нижньому кінці довірчого інтервалу; наприклад, якщо ваше середнє значення$7.4$ з обмеженнями довіри$5.4$ і$9.4$, ваш довірчий інтервал$5.4$ повинен$9.4$. Більшість людей використовують обмеження$95\%$ довіри, хоча ви можете використовувати інші значення. Встановлення$95\%$ довірчих обмежень означає, що якщо ви взяли повторювані випадкові вибірки з популяції та обчислили середні та довірчі межі для кожної вибірки, довірчий інтервал для$95\%$ ваших зразків буде включати параметричне середнє значення.

Щоб проілюструвати це, наведемо засоби та довірчі інтервали для$100$ зразків$3$ спостережень з популяції з параметричним середнім значенням$5$. З$100$ зразків$94$ (показані з$X$ для середнього та тонкої лінії для довірчого інтервалу) мають параметричне середнє в межах свого$95\%$ довірчого інтервалу, а$6$ (показано колами та товстими лініями) мають параметричне середнє за межами довірчого інтервалу.

Мал. 3.4.1 Середні та довірчі інтервали для 100 зразків 3 спостережень

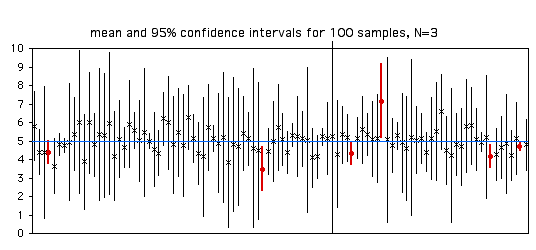
При більших розмірах вибірки$95\%$ довірчі інтервали стають меншими:

Мал. 3.4.2 Середні та довірчі інтервали для 100 зразків із 20 спостережень

Коли ви обчислюєте довірчий інтервал для однієї вибірки, спокусливо сказати, що «існує$95\%$ ймовірність того, що довірчий інтервал включає параметричне середнє». Це технічно невірно, оскільки це означає, що якщо ви збирали зразки з однаковим довірчим інтервалом, іноді вони включали б параметричне середнє значення, а іноді - ні. Наприклад, перший зразок на малюнку вище має довірчі межі$4.59$ і$5.51$. Було б невірно сказати, що того$95\%$ часу параметричне середнє значення для цієї популяції лежало б між$4.59$ і$5.51$. Якби ви взяли повторні зразки з цієї ж популяції і неодноразово отримували довірчі межі$4.59$ і$5.51$, параметричне середнє (тобто$5$, пам'ятайте) було б в цьому інтервалі$100\%$ часу. Деякі статистики не дбають про цю заплутану, педантичну відмінність, але інші дуже прискіпливі до цього, тому добре знати.

Межі довіри для змінних вимірювань

Щоб обчислити довірчі межі для змінної вимірювання, помножте стандартну похибку середнього часу відповідного t-значення. $t$Значення -визначається ймовірністю ($0.05$для$95\%$ довірчого інтервалу) і ступенями свободи ($n-1$). У електронній таблиці ви можете використовувати =( STDEV (Ys) /SQRT (COUNT (Ys))) * TINV (0.05, COUNT (Ys) -1), де$Ys$ діапазон комірок, що містять ваші дані. Ви додаєте це значення і віднімаєте його із середнього значення, щоб отримати межі довіри. Таким чином, якщо середнє значення$87$ і$t$ -значення разів стандартна помилка$10.3$, обмеження довіри будуть$76.7$ і$97.3$. Ви також можете повідомити про це як "$87\pm 10.3$(обмеження$95\%$ довіри).» Люди повідомляють як обмеження довіри, так і стандартні помилки як «$\pm$щось означають», тому завжди обов'язково вказуйте, про що ви говорите.

Все вищесказане відноситься тільки до нормально розподілених змінних вимірювань. Для даних вимірювань з дуже ненормального розподілу, методи початкового завантаження, про які я не буду говорити тут, можуть дати кращі оцінки меж довіри.

Довірчі межі для номінальних змінних

Існує інша, більш складна формула, заснована на біноміальному розподілі, для обчислення довірчих меж пропорцій (номінальні дані). Важливо, що це дає межі довіри, які не симетричні навколо пропорції, особливо для пропорцій, близьких до нуля або одиниці. John Pezzullo має простий у використанні веб-сторінку для довірчих інтервалів пропорції. Щоб побачити, як це працює, скажімо, ви взяли зразок$20$ чоловіків і знайшли$2$ дальтонік і$18$ не дальтонік. Перейдіть на веб-сторінку та введіть$2$ у поле «Чисельник» та$20$ поле «Знаменник», а потім натисніть «Обчислити». Результати для цього прикладу будуть нижньою межею довіри$0.0124$ та верхньою межею довіри$0.3170$. Ви не можете повідомити про частку кольорових сліпих чоловіків як "$0.10\pm something$, натомість вам доведеться сказати"$0.10$ з$95\%$ упевненістю$0.0124$ обмеженнями і»$0.3170$.

Альтернативна методика оцінки довірчих меж пропорції передбачає, що пропорції зразка зазвичай розподілені. Ця приблизна методика дає симетричні межі довіри, які для пропорцій поблизу нуля або одиниці очевидно невірні. Наприклад, якщо ви обчислите межі довіри, використовуючи нормальне наближення$0.10$ з розміром вибірки$20$, ви отримаєте$-0.03$ і$0.23$, що смішно (ви не могли б мати менше, ніж$0\%$ чоловіки, які є дальтоніками). Також було б невірно сказати, що обмеження довіри були$0$ і$0.23$, тому що ви знаєте, що частка дальтоніків у вашому населенні більша, ніж$0$ (у вашому зразку було два дальтоніків, тож ви знаєте, що населення має щонайменше двох дальтоніків). Я вважаю, що обмеження довіри для пропорцій, заснованих на нормальному наближенні, застарілими для більшості цілей; слід використовувати довірчий інтервал, заснований на біноміальному розподілі, якщо розмір вибірки не настільки великий, що обчислювально-непрактичний. На жаль, більше людей використовують межі довіри, засновані на нормальному наближенні, ніж використовують правильні, біноміальні межі довіри.

Формула$95\%$ довірчого інтервалу з використанням нормального наближення -$p$ це$p\pm 1.96\sqrt{\left [ \frac{p(1-p)}{n} \right ]}$, де$n$ пропорція і розмір вибірки. Таким чином, для$P=0.20$ і$n=100$, довірчий інтервал буде$\pm 1.96\sqrt{\left [ \frac{0.20(1-0.20)}{100} \right ]}$, або$0.20\pm 0.078$. Загальне правило говорить, що це нормально використовувати це наближення до тих пір, поки більше, ніж$5$; моє правило$npq$ полягає в тому, щоб використовувати нормальне наближення тільки тоді, коли розмір вибірки настільки великий, що обчислення точного біноміального довірчого інтервалу змушує дим виходити з вашого комп'ютера.

Статистичне тестування з довірчими інтервалами

Цей довідник здебільшого представляє «класичну» або «частотну» статистику, в якій гіпотези перевіряються шляхом оцінки ймовірності отримання спостережуваних результатів випадково, якщо нуль істинно ($P$значення). Альтернативний спосіб ведення статистики полягає в тому, щоб поставити довірчий інтервал на міру відхилення від нульової гіпотези. Наприклад, замість того, щоб порівнювати два засоби з двовибірковим t-тестом, деякі статистики обчислили б довірчий інтервал різниці в середніх.

Цей підхід є цінним, якщо невелике відхилення від нульової гіпотези буде нецікавим, коли вас більше цікавить розмір ефекту, а не те, чи він існує. Наприклад, якщо ви робите остаточне тестування нового препарату, який ви впевнені, матиме певний ефект, ви будете в основному зацікавлені в оцінці того, наскільки добре він працював, і наскільки ви впевнені в розмірі цього ефекту. Ви хочете, щоб ваш результат був «Цей препарат знижував систолічний артеріальний тиск$10.7 mm\; \; Hg$, з довірчим інтервалом$7.8$ до»$13.6$, а не «Цей препарат значно знизив систолічний артеріальний тиск ($P=0.0007$)».

Використання обмежень довіри таким чином, як альтернатива статистиці частот, має багато прихильників, і це може бути корисним підходом. Однак я часто бачу людей, які говорять такі речі, як «Різниця в середньому артеріальному тиску була$10.7 mm\; \; Hg$, з довірчим інтервалом$7.8$ до$13.6$; тому що довірчий інтервал на різницю не включає$0$, засоби значно відрізняються». Це просто незграбний, обхідний спосіб проведення тестування гіпотез, і вони повинні просто визнати це і зробити частотний статистичний тест.

Існує міф, що коли два засоби мають довірчі інтервали, які перекриваються, кошти істотно не відрізняються (на$P<0.05$ рівні). Інша версія цього міфу полягає в тому, що якщо кожне середнє значення знаходиться поза довірчим інтервалом іншого засобу, засоби значно відрізняються. Жоден з них не відповідає дійсності (Schenker and Gentleman 2001, Payton et al. 2003); два набори чисел легко мати перекриваються довірчі інтервали, але все ще значно відрізнятися за допомогою двовибіркового t -тесту; навпаки, кожне середнє значення може бути поза довірчим інтервалом іншого, але вони є все ще істотно не відрізняється. Не намагайтеся порівнювати два засоби, візуально порівнюючи їх довірчі інтервали, просто використовуйте правильний статистичний тест.

Подібна статистика

Межі довіри і стандартна похибка середнього служать одній і тій же меті, щоб висловити достовірність оцінки середнього. Коли ви дивитеся на наукові праці, іноді «смуги помилок» на графіках або ± число після засобів у таблицях представляють стандартну похибку середнього, тоді як в інших роботах вони представляють$95\%$ довірчі інтервали. Я віддаю перевагу$95\%$ інтервалам довіри. Коли я бачу графік з купою точок і смуг помилок, що представляють засоби та довірчі інтервали, я знаю, що більшість ($95\%$) смуг помилок включають параметричні засоби. Коли смуги помилок є стандартними похибками середнього, лише близько двох третин барів, як очікується, включають параметричні засоби; Я повинен подумки подвоїти стовпчики, щоб отримати приблизний розмір$95\%$ довірчого інтервалу (тому що$t(0.05)$ приблизно$2$ для всіх, але дуже малих значень з$n$). Яку б статистику ви не вирішили використовувати, обов'язково дайте зрозуміти, що представляють смуги помилок на ваших графіках. Дивовижна кількість статей не говорить, що представляють їх смуги помилок, а це означає, що єдина інформація, яку смуги помилок передають читачеві, - це те, що автори недбалі та недбалі.

Приклади

Дані вимірювань

Дані чорнозового танцю з центральної веб-сторінки тенденції мають середнє арифметичне значення$70.0$. Нижня межа довіри -$45.3$ ($70.0-24.7$), а верхня межа довіри -$94.7$ ($70+24.7$).

Номінальні дані

Якщо ви працюєте з великою кількістю пропорцій, добре мати приблизне уявлення про обмеження довіри для різних розмірів вибірки, тому ви маєте уявлення про те, скільки даних вам знадобиться для конкретного порівняння. Для пропорцій поруч$50\%$ довірчі інтервали приблизно$\pm 30\%,\; 10\%,\; 3\%$, а$1\%$ для$n=10,\; 100,\; 1000,$ і$10,000$ відповідно. Ось чому «похибка» в політичних опитуваннях, які зазвичай мають розмір вибірки навколо$1,000$, зазвичай приблизно$3\%$. Звичайно, ця груба ідея не замінює фактичного аналізу потужності.

п	пропорція = 0,10	пропорція = 0,50
10	0.0025, 0.4450	0.1871, 0.8129
100	0.0490, 0,1762	0.3983, 0.6017
1000	0.0821, 0.1203	0.4685, 0.5315
10 000	0.0942, 0.1060	0.4902, 0.5098

Як розрахувати довірчі межі

Електронні таблиці

Таблиця описової статистики descriptive.xls обчислює межі$95\%$ довіри середнього для$1000$ вимірювань. Довірчі інтервали для електронної таблиці біноміальної пропорції confidence.xls обчислює$95\%$ довірчі межі для номінальних змінних, використовуючи як точне біноміальне, так і нормальне наближення.

Веб-сторінки

Ця веб-сторінка обчислює довірчі інтервали середнього значення для спостережень до$10,000$ вимірювань. Веб-сторінка для довірчих інтервалів пропорції обробляє номінальні змінні.

Р

$R$Компаньйон Сальваторе Мангіафіко має вибіркові програми R для довірчих обмежень як для вимірювання, так і для номінальних змінних.

САС

Щоб отримати довірчі межі для змінної вимірювання, додайте CIBASIC до оператора PROC UNIVARIATE, ось так:

дані риби; місце
введення $ dacenumber;
карти;
Mill_Creek_1 76
Mill_Creek_2 102
Північ_Філія_Рок_Крик_1 12
Північ_Філія_Рок_Крік_1 12 Північ_Філія_Рок_Крик_2 39
Рок_Крик_1 55
Rock_Creek_2 93
Rock_Creek_3 98
Rock_Creek_4 53
Туреччина_Відділення 102
;
процес одноваріантні дані = риба цибасик;
бігти;

Вихідні дані будуть включати$95\%$ довірчі межі для середнього (а також для стандартного відхилення та дисперсії, які вам навряд чи коли-небудь знадобляться):

Основні межі довіри Припускаючи нормальність

Параметр Оцінка 95% Межі довіри

Середнє 70.00000 45.33665
94.66335 Стандартне відхилення 32.08582 21.67259 61.46908
дисперсія 1030 469.70135 3778

Це показує, що дані чорнозового танцю мають середнє значення$70$, з упевненістю межі$45.3$ і$94.7$.

Ви можете отримати обмеження довіри для біноміальної пропорції за допомогою PROC FREQ. Ось приклад програми з точного тесту на сторінці goodness-of-fit:

дані gus;
вхід лапи $;
карти;

правий лівий правий правий правий
правий

правий
правий
правий
правий
правий
правий
;
proc freq data=gus;
таблиці лапа/біноміальні (P = 0.5);
точний біноміальний;
прогін;

І ось частина виходу:

Біноміальна пропорція
для лапи = ліворуч
-
Пропорція 0.2000
ASE 0.1265
95% Нижня межа Conf 0,0000
95% Верхня межа Конф 0.4479

Точні межі Конф
95% Нижня межа Конф 0,0252
95% Верхня межа Конф 0.5561

Перша пара показаних довірчих меж заснована на нормальному наближенні; друга пара краща, заснована на точному біноміальному обчисленні. Зверніть увагу, що якщо у вас більше двох значень номінальної змінної, довірчі межі будуть розраховані тільки для значення, ім'я якого спочатку в алфавітному порядку. Наприклад, якщо набір даних Gus включав значення «ліворуч», «праворуч» та «обидва», SAS обчислить лише обмеження довіри щодо частки «обох». Одним з незграбних способів вирішити цю проблему було б запустити програму три рази, змінивши назву «ліворуч» на «лівий», а потім змінивши назву «праворуч» на «праворуч», щоб зробити кожну з них першим за один прогін.

Посилання

1. Пейтон, М.Е., Грінстоун М.Х., і Н.Шенкер. 2003. Перекриття довірчих інтервалів або стандартних інтервалів помилок: що вони означають з точки зору статистичної значущості? Журнал науки про комах 3:34.
2. Шенкер, Н., і Дж.Ф. Джентльмен. 2001 рік. Про судження значущості відмінностей шляхом вивчення перекриття між довірчими інтервалами. Американський статистик 55:182-186.