3.3: Стандартна помилка середнього

Last updated
Save as PDF

Page ID: 98731

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Стандартна похибка середнього означає, наскільки точною є ваша оцінка середнього значення.

Вступ

Коли ви берете вибірку спостережень з популяції та обчислюєте середнє значення вибірки, ви оцінюєте параметричне середнє або середнє значення всіх індивідів у популяції. Значення вашого зразка не буде точно рівним параметричному значенню, яке ви намагаєтеся оцінити, і ви хотіли б мати уявлення про те, наскільки близьким є ваше середнє значення зразка. Якщо ваш розмір вибірки невеликий, ваша оцінка середнього значення не буде такою ж хорошою, як оцінка, заснована на більшому розмірі вибірки. Ось\(10\) випадкові зразки з модельованого набору даних з істинним (параметричним) середнім значенням\(5\). Вони\(X's\) являють собою окремі спостереження, червоні кола - це вибіркові засоби, а синя лінія - параметричне середнє.

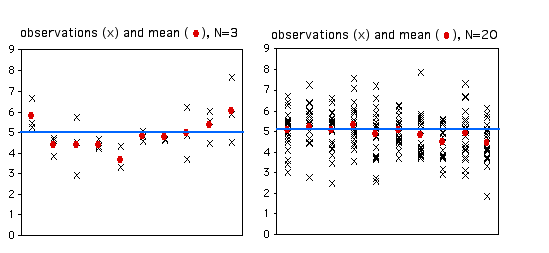
Мал. 3.3.1 Індивідуальні спостереження (X) і засоби (червоні точки) для випадкових вибірок з популяції з параметричним середнім значенням 5 (горизонтальна лінія).

Як бачите, лише з розміром\(3\) вибірки деякі засоби вибірки не дуже близькі до параметричного середнього. Перша вибірка виявилася трьома спостереженнями, які були більшими\(5\), тому середнє значення вибірки занадто високе. Другий зразок має три спостереження, які були менше\(5\), тому середнє значення вибірки занадто низьке. При\(20\) спостереженнях за зразком кошти вибірки, як правило, ближче до параметричного середнього.

Після того, як ви розрахували середнє значення вибірки, ви повинні повідомити людям, наскільки близьке середнє значення зразка, ймовірно, буде до параметричного середнього. Один із способів зробити це - зі стандартною похибкою середнього. Якщо взяти багато випадкових вибірки з популяції, стандартною похибкою середнього значення є стандартним відхиленням різних засобів вибірки. Близько двох третин (\(68.3\%\)) вибіркових засобів знаходилися б в межах однієї стандартної помилки параметричного середнього, знаходилися\(95.4\%\) б у межах двох стандартних помилок, і майже всі (\(99.7\%\)) були б у межах трьох стандартних помилок.

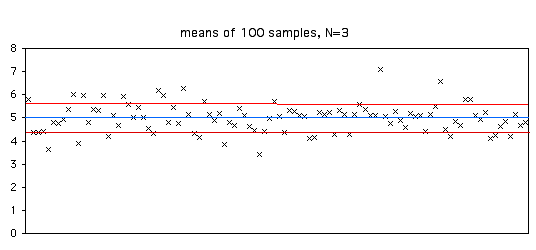
Мал. 3.3.2 Середні 100 випадкових вибірок (N=3) з популяції з параметричним середнім значенням 5 (горизонтальна лінія).

Ось малюнок, що ілюструє це. Я взяв\(100\) зразки\(3\) з популяції з параметричним середнім значенням\(5\) (показана синьою лінією). Стандартне відхилення\(100\) кошти було\(0.63\). З\(100\) вибіркових засобів,\(70\) знаходяться між\(4.37\) і\(5.63\) (параметричне середнє\(\pm\) одна стандартна похибка).

Зазвичай у вас не буде декількох зразків для використання при складанні декількох оцінок середнього. На щастя, ви можете оцінити стандартну похибку середнього значення, використовуючи розмір вибірки і стандартне відхилення однієї вибірки спостережень. Стандартна похибка середнього оцінюється стандартним відхиленням спостережень, поділеним на квадратний корінь розміру вибірки. Чомусь немає функції електронної таблиці для стандартної помилки, тому ви можете використовувати =STDEV (Ys) /SQRT (COUNT (Ys)), де\(Ys\) діапазон комірок, що містять ваші дані.

Ця цифра така ж, як і вище, тільки цього разу я додав смуги помилок, що вказують на\(\pm 1\) стандартну помилку. Оскільки оцінка стандартної помилки базується лише на трьох спостереженнях, вона сильно варіюється від зразка до вибірки.

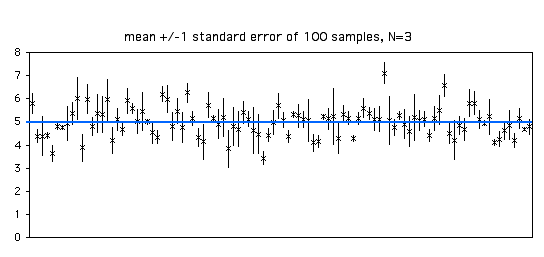
Мал. 3.3.3 Означає ± 1 стандартну похибку 100 випадкових зразків (n=3) з популяції із середнім параметричним значенням 5 (горизонтальна лінія).

При розмірі вибірки\(20\), кожна оцінка стандартної помилки є більш точною. З\(100\) зразків на графіку нижче\(68\) включають параметричне середнє в межах\(\pm 1\) стандартної похибки середнього зразка.

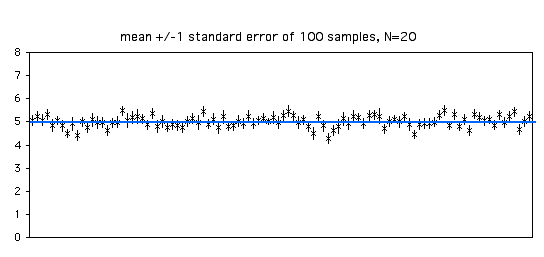
Мал. 3.3.4 Означає ± 1 стандартну похибку 100 випадкових зразків (N=20) з популяції із середнім параметричним значенням 5 (горизонтальна лінія).

У міру збільшення розміру вибірки стандартна похибка середнього значення стане меншою. При більших розмірах вибірки середнє значення вибірки стає більш точною оцінкою середнього параметричного, тому стандартна похибка середнього стає меншою. Зауважте, що це функція квадратного кореня розміру вибірки; наприклад, щоб зробити стандартну помилку вдвічі більшою, вам знадобиться в чотири рази більше спостережень.

«Стандартна похибка середнього» і «стандартне відхилення середнього» - еквівалентні терміни. Люди майже завжди говорять «стандартна похибка середнього», щоб уникнути плутанини зі стандартним відхиленням спостережень. Іноді «стандартна помилка» використовується сама по собі; це майже напевно вказує на стандартну похибку середнього, але оскільки є також статистика стандартної похибки дисперсії, стандартної похибки медіани, стандартної похибки коефіцієнта регресії тощо, слід вказати стандартну похибку середнього.

Існує міф, що коли два засоби мають стандартні смуги помилок, які не перекриваються, засоби значно відрізняються (на\(P<0.05\) рівні). Це неправда (Browne 1979, Payton et al. 2003); два набори чисел легко мати стандартні смуги помилок, які не перекриваються, але не суттєво відрізняються за допомогою двовибіркового t -тесту. Не намагайтеся робити статистичні тести, візуально порівнюючи стандартні смуги помилок, просто використовуйте правильний статистичний тест.

Подібна статистика

Довірчі інтервали і стандартна похибка середнього служать одній і тій же меті, щоб висловити достовірність оцінки середнього. Коли ви дивитеся на наукові праці, іноді «смуги помилок» на графіках або\(\pm\) число після засобів у таблицях представляють стандартну похибку середнього, тоді як в інших роботах вони представляють\(95\%\) довірчі інтервали. Я віддаю перевагу\(95\%\) інтервалам довіри. Коли я бачу графік з купою точок і смуг помилок, що представляють засоби та довірчі інтервали, я знаю, що більшість (\(95\%\)) смуг помилок включають параметричні засоби. Коли смуги помилок є стандартними помилками середнього, очікується, що лише близько двох третин смуг помилок включають параметричні засоби; Я повинен подумки подвоїти бари, щоб отримати приблизний розмір\(95\%\) довірчого інтервалу. Крім того, для дуже малих розмірів вибірки\(95\%\) довірчий інтервал більше, ніж в два рази перевищує стандартну похибку, а поправочний коефіцієнт ще складніше зробити в голові. Яку б статистику ви не вирішили використовувати, обов'язково дайте зрозуміти, що представляють смуги помилок на ваших графіках. Я бачив багато графіків у наукових журналах, які не дали поняття про те, що представляють смуги помилок, що робить їх досить марними.

Ви використовуєте стандартне відхилення та коефіцієнт варіації, щоб показати, скільки варіацій існує серед окремих спостережень, тоді як ви використовуєте стандартні похибки або довірчі інтервали, щоб показати, наскільки хороша ваша оцінка середнього. Єдиний раз, коли ви повідомите про стандартне відхилення або коефіцієнт варіації, буде, якщо ви насправді зацікавлені в кількості варіації. Наприклад, якщо ви вирощували купу соєвих рослин з двома різними видами добрив, ваш основний інтерес, ймовірно, полягав би в тому, чи була врожайність сої різною, тож ви повідомите про середню врожайність ± або стандартну похибку, або довірчі інтервали. Якщо ви збиралися робити штучний відбір на сою для розведення для кращого врожаю, вас може зацікавити, яка обробка мала найбільшу варіацію (полегшує вибір найбільш швидкозростаючої сої), тож тоді ви повідомите про стандартне відхилення або коефіцієнт варіації.

Немає сенсу повідомляти як стандартну помилку середнього, так і стандартного відхилення. Поки ви повідомляєте про один з них, плюс розмір вибірки (\(N\)), кожен, кому потрібно, може обчислити інший.

Приклад

Стандартною похибкою середнього значення для даних чорнозового танцю з центральної веб-сторінки тенденції є\(10.70\).

Як розрахувати стандартну похибку

Електронна таблиця

Таблиця описової статистики descriptive.xls обчислює стандартну похибку середнього значення для\(1000\) спостережень, використовуючи функцію =STDEV (Ys) /SQRT (COUNT (Ys)).

Веб-сторінки

Ця веб-сторінка обчислює стандартну похибку середньої та іншої описової статистики для\(10,000\) спостережень.

Ця веб-сторінка обчислює стандартну похибку середнього значення разом з іншою описовою статистикою. Я не знаю максимальної кількості спостережень, які він може обробити.

Р

\(R\)Компаньйон Сальваторе Мангіафіко має зразок програми R для стандартної помилки середнього.

САС

PROC UNIVARIATE обчислить стандартну похибку середнього значення. Приклади див. на веб-сторінці центральної тенденції.

Посилання

Браун, Р.Х. 1979. Про візуальну оцінку значущості середньої різниці. Біометрія 35:657-665.
Пейтон, М.Е., Грінстоун М.Х., і Н.Шенкер. 2003. Перекриття довірчих інтервалів або стандартних інтервалів помилок: що вони означають з точки зору статистичної значущості? Журнал науки про комах 3:34.