3.3: PACF причинно-наслідкового процесу ARMA

У цьому розділі введено часткову автокореляційну функцію (PACF) для подальшої оцінки структури залежності стаціонарних процесів загалом та причинно-наслідкових процесів АРМА зокрема. Для початку обчислимо ACVF процесу ковзної середньої порядку$q$

Приклад$\PageIndex{1}$: The ACVF of an MA($q$) process

$(X_t\colon t\in\mathbb{Z})$Дозволяти бути MA ($q$) процес, заданий поліномом$\theta(z)=1+\theta_1z+\ldots+\theta_qz^q$. Потім, дозволяючи$\theta_0=1$, він тримає, що

$$E[X_t]=\sum_{j=0}^q\theta_jE[Z_{t-j}]=0. \nonumber$$

Рішення

Щоб обчислити ACVF, припустимо, що$h\geq 0$ і запишіть

\ begin {вирівнювати*}
\ гамма (h) &= Cov (X_ {t+h}, X_ {t}) =Е [X_ {t+h} X_ {t}]\\ [.2см]
&= Е\ ліворуч [\ sum_ {j=0} ^q\ theTa_JZ_ {t+h-j}\ праворуч)
\ ліворуч (\ сума _ {k=0} ^q\ тета_kz_ {t-k}\ право)\\ праворуч]\\ [.2см]
&=\ сума {j=0} ^q\ sum_ {k=0} ^q\ тета_j\ тета_ке [Z_ {t+h-j} Z_ {t-k}]\\ [ .2см]
&=\ ліворуч\ {\ почати {масив} {l@ {\ qquad} r}
\ стиль відображення\ сигма ^ 2\ sum_ {k=0} ^ {q-h}\ theta_ {k+h}\ theta_k,
& 0\ leq h\ leq q.\\ [.2см]
0, & h>q.
\ кінець {масив}\.
\ end {вирівнювати*}

Результатом тут є узагальнення випадку МА (1), який розглядався в прикладі 3.2.3. Це також окремий випадок лінійного процесу в прикладі 3.1.4. Структура ACVF для процесів МА вказує на можливу стратегію визначення на практиці невідомого порядку$q$: побудуйте зразок АКФ і виберіть в якості порядку$q$ найбільший лаг такий, який значно$\rho(h)$ відрізняється від нуля.

Хоча зразок ACF потенційно може виявити справжній порядок процесу МА, те ж саме більше не відповідає дійсності у випадку процесів AR. Навіть для часового ряду AR (1) було показано в прикладі 3.2.1, що його ACF$\rho(h)=\phi^{|h|}$ є ненульовим для всіх лагів. Однак в якості подальшої мотивації ми обговорюємо наступний приклад.

Приклад 3.3.2

$(X_t\colon t\in\mathbb{Z})$Дозволяти причинний AR (1) процес з параметром$|\phi|<1$. Він стверджує, що

\ [\ гамма (2) =Cov (X_2, X_ {0})
=Cov (\ Phi^2x_ {0} +\ phi Z_ {1} +Z_2, X_ {0})
=\ phi^2\ гамма (0)\ not=0. \ номер\]

Щоб розірвати лінійну залежність між$X_0$ і$X_2$, відніміть$\phi X_1$ з обох змінних. Розрахунок результуючої коваріації прибутковості

$$Cov(X_2-\phi X_{1},X_0-\phi X_1)= Cov(Z_2,X_0-\phi X_1)=0, \nonumber$$

оскільки, через причинність цього процесу AR (1),$X_0-\phi X_1$ є функцією$Z_{1},Z_0,Z_{-1},\ldots$ і, отже, не корелює з$X_2-\phi X_1=Z_2$.

Попередній приклад мотивує наступне загальне визначення.

Визначення 3.3.1 Часткова автокореляційна функція

$(X_t\colon t\in\mathbb{Z})$Дозволяти бути слабо стаціонарним стохастичним процесом з нульовим середнім. Потім послідовність,$(\phi_{hh}\colon h\in\mathbb{N})$ задана

\ begin {align*}
\ phi_ {11} &=\ rho (1) =Corr (X_1, X_0),\\ [.2см]
\ phi_ {hh} &=Corr (x_H-x_h^ {h-1}, X_0-X_0^ {h-1}),\ qquad
h\ geq 2,
\ end {align*}

називається частковою автокореляційною функцією (PACF)$(X_t\colon t\in\mathbb{Z})$.

У ньому,

\ begin {align*}
x_h^ {h-1} &=\ mbox {регресія $x_H$ на
} (X_ {h-1},\ ldots, X_1)\\ [.2см]
&=\ beta_1x_ {h-1} +\ beta_2x_ {h-2} +\ ldots+\ beta_ {h-1}\ [.3см]
X_0^ {h-1} &=\ mbox {регресія $X_0$ на
} (X_1,\ ldots, X_ {h-1})\\ [.2см]
&=\ бета_1x_1+\ бета_2+\ ldots+\ бета_ {h-1} X_ {h-1}.
\ end {вирівнювати*}

Зверніть увагу, що$\beta_0$ в параметрах регресії немає коефіцієнта перехоплення, оскільки передбачається, що$E[X_t]=0$. Наступний приклад демонструє, як обчислити параметри регресії у випадку процесу AR (1).

Рисунок 3.5 ACF та PACF процесу AR (2) (верхня панель) та MA (3) (середня панель) та процесу ARMA (1,1) (нижня панель).

Приклад 3.3.3 PACF процесу AR (1)]

Якщо$(X_t\colon t\in\mathbb{Z})$ є причинним AR (1) процес, то$\phi_{11}=\rho(1)=\phi$. Щоб розрахувати$\phi_{22}$, спочатку розрахуйте$X_2^1=\beta X_1$, тобто$\beta$. Цей коефіцієнт визначається мінімізацією середньоквадратичної похибки між$X_2$ і$\beta X_1$:

$$E[X_2-\beta X_1]^2=\gamma(0)-2\beta\gamma(1)+\beta^2\gamma(0) \nonumber$$

який зводиться до мінімуму$\beta=\rho(1)=\phi$. (Це слід легко, взявши похідну і встановивши її на нуль.) Тому$X_2^1=\phi X_1$. Аналогічно, один обчислює,$X_0^1=\phi X_1$ і це випливає з Прикладу 3.3.2, що$\phi_{22}=0$. Дійсно, всі$h\geq 2$ лаги PACF дорівнюють нулю.

Більш загально розглянемо коротко причинно-наслідковий процес AR ($p$), заданий$\phi(B)X_t=Z_t$ з$\phi(z)=1-\phi_1z-\ldots-\phi_pz^p$.

Тоді, для того$h>p$,

$$X_h^{h-1}=\sum_{j=1}^p\phi_jX_{h-j} \nonumber$$

і, отже,

$$\phi_{hh}=Corr(X_h-X_h^{h-1},X_0-X_0^{h-1}) = Corr(Z_h,X_0-X_0^{h-1})=0 \nonumber$$

if$h>p$ за причинністю (той самий аргумент, який використовується в прикладі 3.3.2, застосовується і тут). Однак дотримуйтесь, що$\phi_{hh}$ це не обов'язково нуль, якщо$h\leq p$. Вищесказане припускає, що вибіркова версія PACF може бути використана для визначення порядку авторегресивного процесу з даних: використовувати як$p$ найбільший відставання,$h$ такий, який значно$\phi_{hh}$ відрізняється від нуля.

З іншого боку, для інвертованого процесу MA ($q$) можна написати$Z_t=\pi(B)X_t$ або, що еквівалентно,

$$X_t=-\sum_{j=1}^\infty\pi_jX_{t-j}+Z_t \nonumber$$

що показує, що PACF процесу MA ($q$) буде ненульовим для всіх лагів, оскільки для ``ідеальної» регресії доведеться використовувати всі минулі змінні$(X_s\colon s<t)$ замість лише кількості,$X_t^{t-1}$ наведеної у визначенні 3.3.1.

Підсумовуючи, PACF змінює поведінку ACVF для процесів авторегресії та ковзного середнього. Хоча останні мають ACVF, який зникає після відставання$q$ і PACF, який є ненульовим (хоча і розпадається) для всіх лагів, процеси AR мають ACVF, який є ненульовим (хоча і розпадається) для всіх лагів, але PACF, який зникає після відставання$p$.

ACVF (ACF) та PACF, отже, надають корисні інструменти для оцінки залежності заданих процесів ARMA. Якщо оцінений ACVF (розрахунковий PACF) по суті дорівнює нулю після деякого часового відставання, то базовий часовий ряд може бути зручно змодельований за допомогою процесу MA (AR) - і жодна загальна послідовність ARMA не повинна бути встановлена. Ці висновки зведені в табл. 3.3.1

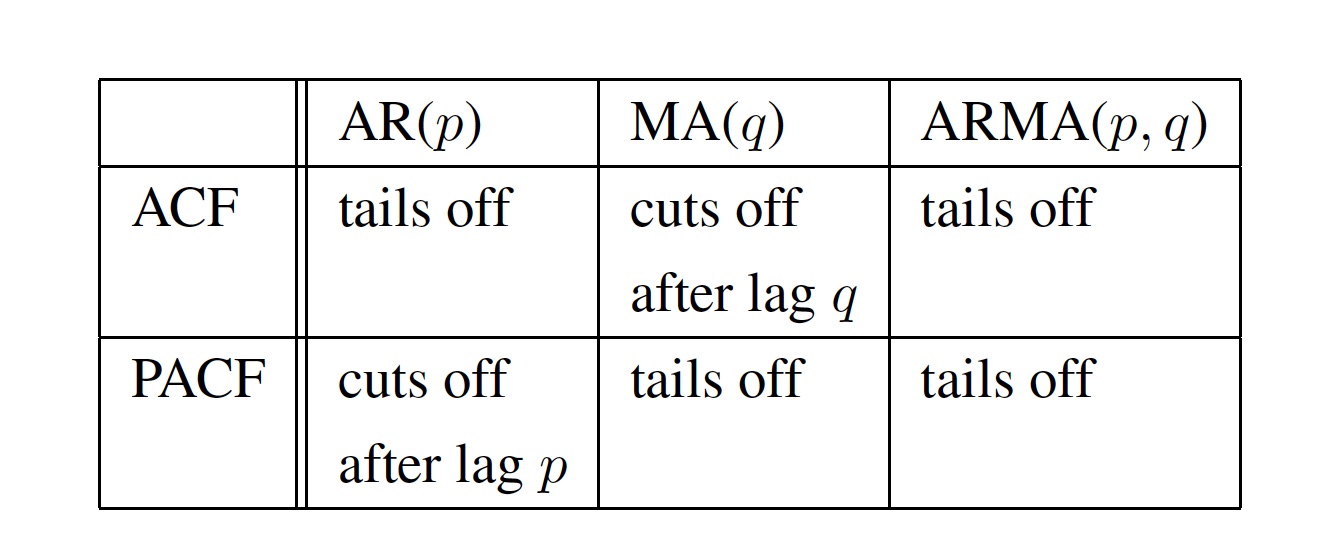
Таблиця 3.1: Поведінка ACF та PACF для процесів AR, MA та ARMA.

Приклад 3.3.4

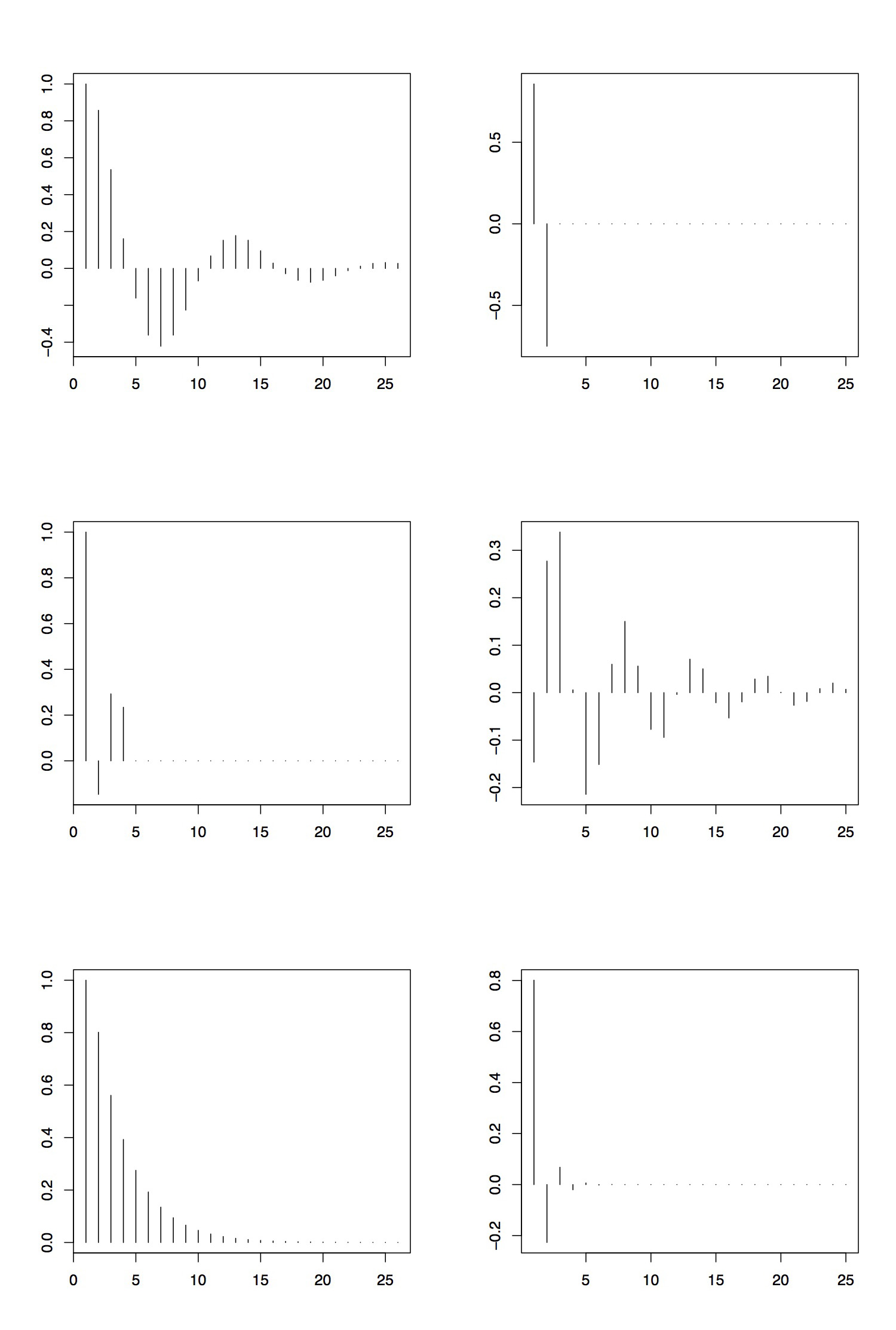
Рисунок 3.5 збирає ACF та PACF трьох процесів ARMA. Верхня панель береться з процесу AR (2) з параметрами$\phi_1=1.5$ і$\phi_2=-.75$. Видно, що АКФ відходить і відображає циклічну поведінку (зверніть увагу, що відповідний авторегресивний поліном має складні коріння). PACF, однак, відсікає після відставання 2. Таким чином, оглядаючи ACF і PACF, ми б правильно вказували порядок процесу АР.

Середня панель показує ACF і PACF процесу MA (3), заданого параметрами$\theta_1=1.5$,$\theta_2=-.75$ і$\theta_3=3$. Ділянки підтверджують це,$q=3$ оскільки ACF відрізається після відставання 3, а PACF хвости.

Нарешті, на нижній панелі відображаються ACF і PACF процесу ARMA (1,1) Приклад 3.2.4. Тут оцінка набагато складніше. У той час як ACF хвости, як передбачалося (див. Таблицю 3.1), PACF в основному відсікає після відставання 4 або 5. Це може призвести до неправильного висновку, що основний процес насправді є процесом AR порядку 4 або 5. (Причина такої поведінки полягає в тому, що залежність у цьому конкретному процесі ARMA (1,1) може бути добре наближена до залежності часового ряду AR (4) або AR (5).)

Щоб відтворити графіки в R, можна скористатися командами

> AR2.acf = Арма АФ (ар=с (1,5, -.75), ма = 0, 25)

> AR2.pacf = Арма АФ (ар=с (1,5, -.75), ма = 0, 25, ПАКФ = Т)

для процесу AR (2). Інші два випадки випливають з простих адаптацій цього коду.

Малюнок 3.6: Набір серії Приклад 3.3.5 (зліва), його зразок ACF (середній) і зразок PACF (праворуч).

Малюнок 3.7: Матриця Scatterplot, що стосується поточного набору до минулого набору для лагів$h=1,\ldots,12$.

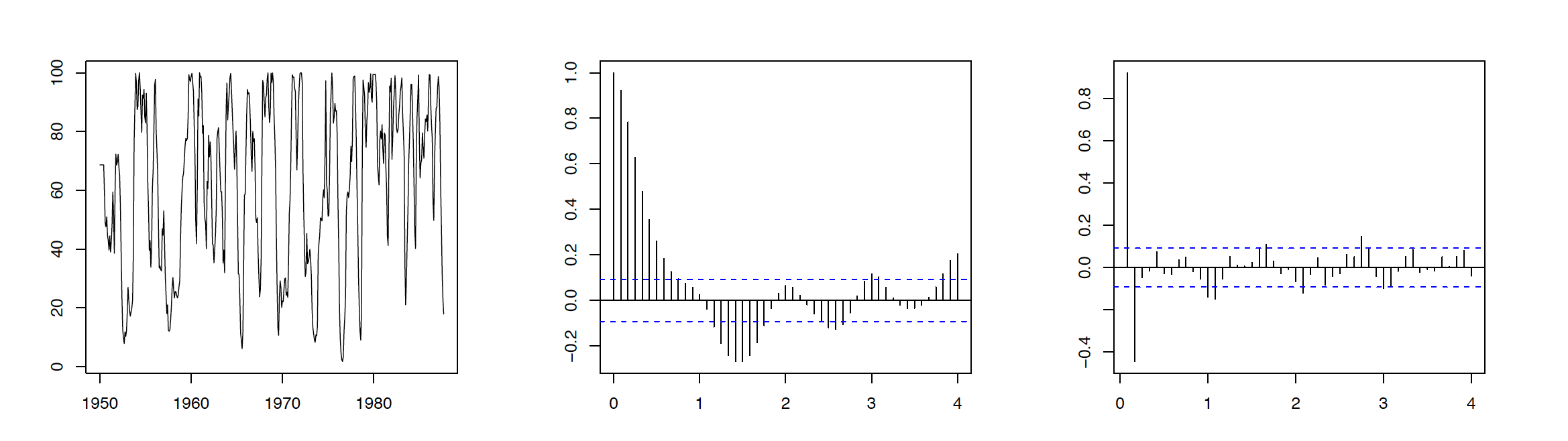
Приклад 3.3.5 Серія набору

Дані, що розглядаються в цьому прикладі, складаються з 453 місяців спостережуваного набору (кількості нових риб) у певній частині Тихого океану, зібраних за 1950—1987 роки. Відповідний графік часових рядів наведено на лівій панелі малюнка 3.6. Відповідні ACF та PACF, відображені на середній та правій панелі одного і того ж малюнка, рекомендують пристосувати процес замовлення AR$p=2$ до даних набору персоналу. Припускаючи, що дані знаходяться в rec, код R для відтворення Рисунок 3.6

> rec = ts (REC, початок = 1950, частота = 12)

> сюжет (rec, xlab = "», Ylab = "»)

> акф (рек, лаг = 48)

> пакет (червоний, лаг = 48)

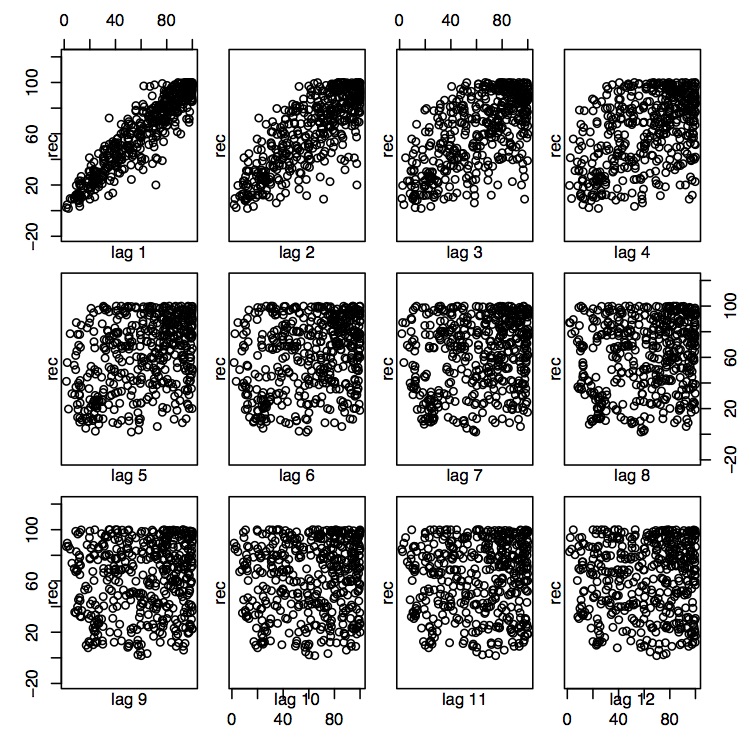
Це твердження також узгоджується з розсіювачами, які пов'язують поточний набір до минулого набору в кілька часових відставань, а саме$h=1,\ldots,12$. Для відставання 1 і 2, здається, існує сильна лінійна залежність, тоді як це вже не так$h\geq 3$. Відповідними командами R є:

> лаг.сюжет (rec, лаги = 12, макет = c (3,4), діаг = F)

Позначимо$X_t$ по набору на час$t$. Для оцінки параметрів AR (2) виконайте регресію на спостережуваних триплетах даних, включених$(x_t,x_ t-1,x_ t-2)\colon j=3,\ldots,453$ до множини, щоб відповідати моделі форми

$$X_t=\phi_0+\phi_1X_ t-1+\phi_2X_ t-2+Z_t, \qquad t=3,\ldots,453, \nonumber$$

де$(Z_t)\sim\mathrm WN(0,\sigma^2)$. Це завдання можна виконати в R наступним чином.

> fit.rec = ar.ols (REC, AIC = F, замовлення.max = 2, поведінка = F, перехоплення = T)

Ці оцінки можна оцінити командою {\ tt fit.rec} і відповідними стандартними помилками з$\tt fit.rec{\$}asy.se$. Тут параметри$\hat{\phi}_0=6.737(1.111)$ оцінюють$\hat{\phi}_1=1.3541(.042)$,$\hat{\phi}_2=-.4632(.0412)$ і$\hat{\sigma}^2=89.72$ виходять. Стандартні помилки наведені в дужках.