1: Статистичні міркування
- Page ID
- 97380
Знайдіть хвилинку, щоб візуалізувати людство в повному обсязі, від самих ранніх людей до сьогодення. Як би ви охарактеризували благополуччя людства? Думайте поза останніми історіями в новині. Щоб допомогти прояснити, подумайте про лікування, житло, транспорт, освіту та наші знання. Хоча не можна заперечувати, що у нас є деякі проблеми, яких не існувало в попередніх поколіннях, ми також маємо значно більше знань.
Прогрес, досягнутий людством у вивченні себе, нашого світу та нашого Всесвіту, підживлюється бажанням людей вирішувати проблеми або здобути розуміння. Він фінансувався як державними, так і приватними грошима. Це було досягнуто завдяки постійному процесу, коли люди пропонують теорії та інші намагаються спростувати теорії, використовуючи докази. Теорії, які не спростовані, стають частиною нашого колективного знання. Жодна людина цього не досягла, це були колективні зусилля людства.
Наскільки ми знаємо і досягли, є багато чого, чого ми не знаємо і ще не досягли. Є багато різних організацій та установ, які сприяють здобуткам людства в знаннях, однак одна організація виділяється тим, що кидає виклик людству, щоб досягти ще більшого. Ця організація є XPrize.1 На своїй веб-сторінці вони пояснюють, що вони є інноваційним двигуном. Фасилітатор експоненціальних змін. Каталізатор на благо людства». Ця організація кидає виклик людству вирішувати сміливі проблеми, проводячи змагання та надаючи грошовий приз команді-переможцю. Приклади деяких їх змагань включають:
- 2004: Ansari XPrize (10 мільйонів доларів) - Private Space Travel - побудувати надійний, багаторазовий, приватно фінансуваний, пілотований космічний корабель, здатний перевозити трьох людей до 100 кілометрів над поверхнею Землі двічі протягом двох тижнів.
- Поточна: XPrize для дорослих грамотності Фонду Барбари Буш (7 мільйонів доларів) - «складні команди для розробки мобільних додатків для існуючих смарт-пристроїв, які призводять до найбільшого підвищення навичок грамотності серед дорослих учнів, які беруть участь всього за 12 місяців».
За оцінками, 36 мільйонів дорослих американців з рівнем читання нижче рівня третього класу. Вони мають труднощі з читанням казок перед сном, читання рецептів та заповнення заяв про роботу, серед іншого. Розробка хорошого додатка може мати величезні переваги для багатьох людей, що також надасть переваги для країни.
Наступна вигадана історія познайомить вас з тим, як дані та статистика використовуються для тестування теорій та прийняття рішень. Мета полягає в тому, щоб ви побачили, що розумові процеси не є алгебраїчними і що необхідно розробити нові способи мислення, щоб ми могли підтвердити наші теорії або приймати рішення, засновані на доказах.
Історія премії грамотності дорослих
Уявіть, що ви є частиною команди, яка змагається за Xprize грамотності для дорослих. На ранніх етапах розробки мета вашої команди - створити додаток, який буде цікавим для користувача, щоб він часто використовував його. Ви протестували свою першу версію (версія 1) програми на деяких дорослих, яким не вистачало базової грамотності, і виявили, що вона використовувалася в середньому 6 годин протягом першого місяця. Ваша команда вирішила, що це не дуже вражає, і що ви можете зробити краще, тому ви розробили абсолютно нову версію програмного забезпечення, позначеного як Версія 2. Коли настав час протестувати програмне забезпечення, 10 членів вашої команди кожен дав його 8 різним людям з низькими навичками грамотності. Ця група з 80 осіб, які отримали програмне забезпечення, є невеликою підмножиною або зразком усіх тих, хто має низькі навички грамотності. Мета полягала в тому, щоб визначити, чи використовується версія 2 більше, ніж в середньому 6 годин на місяць.
Хоча дані в кінцевому підсумку будуть об'єднані разом, ваші товариші по команді вирішують конкурувати один з одним, щоб визначити, чия група з 8 робить краще. Результати наведені в таблиці нижче. Стовпець праворуч - це середнє значення (середнє значення) даних у рядку. Середнє значення знаходять шляхом додавання чисел у рядку та ділення цієї суми на 8.
| Член команди | Версія 2 Дані (годин використання за 1 місяць) | Середнє | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ти, Читач | 4.4 | 3.8 | 4.4 | 6.7 | 1.1 | 5.7 | 0.8 | 2.5 | 3.675 |
| Бетті | 11 | 8.4 | 8.4 | 2.7 | 4.4 | 8.4 | 5.7 | 4.4 | 6.675 |
| Радість | 1.6 | 2.2 | 12.5 | 5.7 | 2.2 | 6.6 | 0.8 | 0.3 | 3.9875 |
| Керісса | 16.1 | 11.1 | 8.7 | 9.1 | 1.4 | 9.1 | 1.2 | 14.4 | 8.8875 |
| Кристал | 0 | 2.1 | 0 | 3.2 | 0.2 | 1.8 | 9.1 | 3.3 | 2.4625 |
| Марцин | 2.2 | 6.3 | 1.3 | 8.8 | 0.8 | 2.7 | 0.9 | 0.8 | 2.975 |
| Тиса | 8.8 | 5.8 | 9.7 | 2.8 | 3.2 | 0.9 | 0.1 | 16.1 | 5.925 |
| Тайлер | 11 | 0.9 | 11.3 | 6.6 | 0.3 | 5.9 | 1.7 | 1.9 | 4.95 |
| Патрік | 0.9 | 1.8 | 6.3 | 3.1 | 6.1 | 6.3 | 3.2 | 6.7 | 4.3 |
Один із способів зрозуміти дані - це їх графік. Графік праворуч називається гістограмою. Він показує розподіл кількості часу, коли програмне забезпечення було використано кожним учасником. Щоб інтерпретувати цей графік, зверніть увагу, що шкала на горизонтальній (x) осі розраховується на 2. Ці цифри представляють години використання. Висота кожного рядка показує, скільки часу використання припадає між значеннями x. Наприклад, 26 людей використовували додаток від 0 до 2 годин, а 2 люди використовували додаток між 16 і 18 годинами.
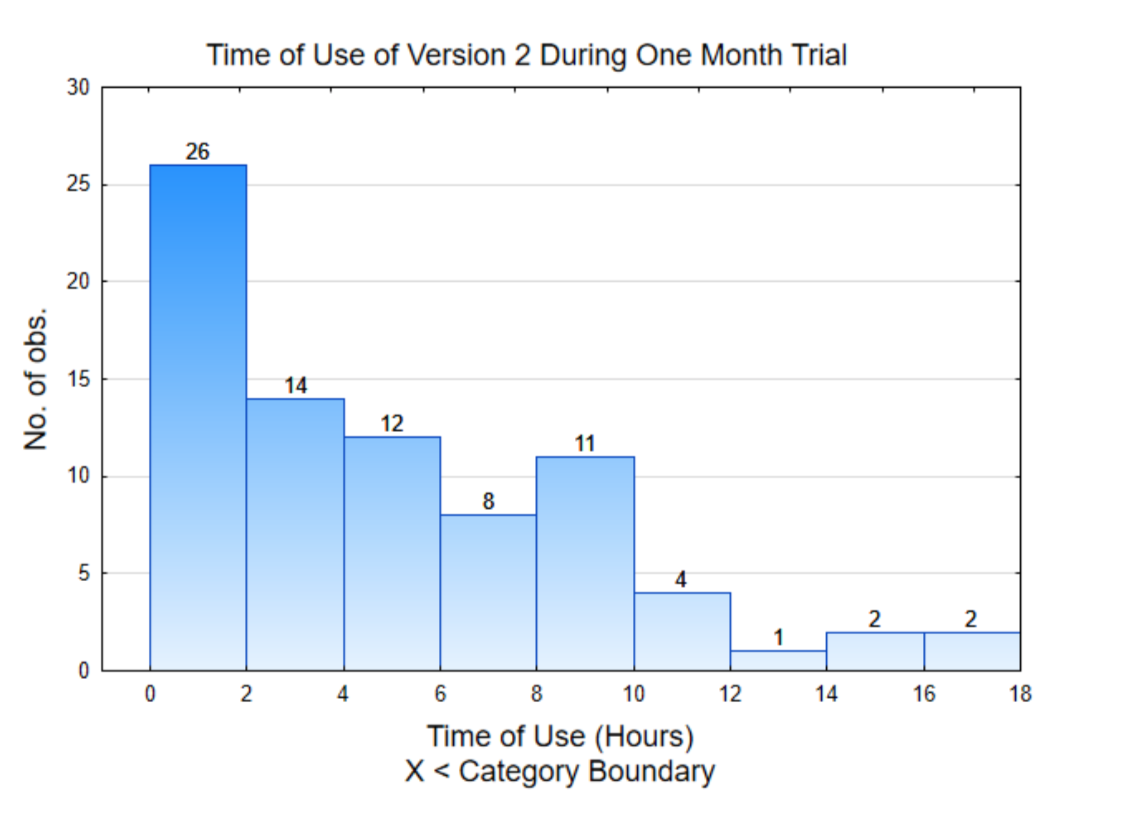
Другий графік являє собою гістограму середнього (середнього) для кожної з 10 груп. Це графік стовпця в таблиці, який затінений. Гістограма засобів називається розподілом вибірки. Розподіл праворуч показує, що 4 засоби знаходяться від 2 до 4 годин, тоді як лише одне середнє значення було від 8 до 10 годин. Зверніть увагу, як засоби згруповані ближче один до одного, ніж вихідні дані.
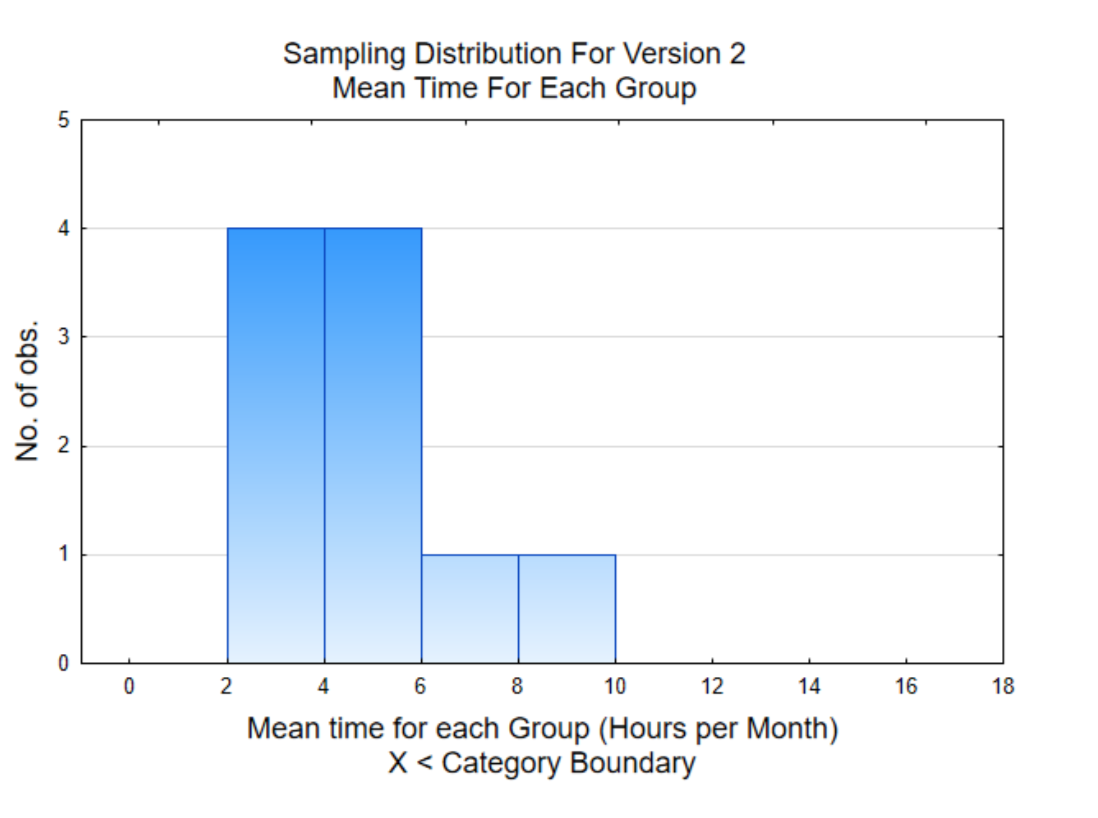
Загальне середнє значення для 80 значень даних становить 4.88 годин. Наше завдання полягає в тому, щоб використовувати графіки та загальне середнє значення, щоб вирішити, чи використовується версія 2 більше, ніж використовувалася версія 1 (6 годин на місяць). Який ваш висновок? Дайте відповідь на це питання, перш ніж продовжувати читання.
Так Версія 2 краще, ніж версія 1 Ні, Версія 2 не краще, ніж версія 1
Що з перерахованого найбільше вплинуло на ваше рішення?
______ 54 з 80 значень даних були нижче 6
______ Середнє значення даних становить 4,88, що нижче 6
______ 8 з 10 зразка засобів нижче 6.
Версія 3
Версія 3 була тотальним редизайном програмного забезпечення. Аналогічна стратегія тестування була використана, як і в попередній версії. Коли ви отримали дані від 8 користувачів, яким ви надали програмне забезпечення, ви виявили, що середня тривалість використання становить 10.25 годин. Виходячи з ваших результатів, чи вважаєте ви, що ця версія краще, ніж версія 1?
| Член команди | Версія 3 Дані (годин використання за 1 місяць) | Середнє | |||||||
| Ти, Читач | 14 | 13 | 8 | 4 | 8 | 21 | 3 | 11 | 10.25 |
Так Версія 3 краще, ніж версія 1 Ні, Версія 3 не краще, ніж версія 1
Ваш колега Кір подивився на її дані, які наведені в таблиці нижче. До якого висновку прийшла б Кір, виходячи з її даних?
| Член команди | Версія 3 Дані (годин використання за 1 місяць) | Середнє | |||||||
| Кір | 0 | 3 | 2 | 3 | 5 | 4 | 8 | 11 | 4. |
Так Версія 3 краще, ніж версія 1 Ні, Версія 3 не краще, ніж версія 1
Якщо ваша інтерпретація ваших даних та даних Кіра є типовою, ви б зробили висновок, що версія 3 була кращою за версію 1 на основі ваших даних, а версія 3 не була кращою на основі даних Кіра. Це ілюструє, як різні зразки можуть призвести до різних висновків. Зрозуміло, що висновок, заснований на ваших даних, і висновок, заснований на даних Кіра, не можуть бути правильними. Щоб допомогти оцінити, хто може помилятися, давайте розглянемо всі дані для 80 людей, які протестували версію 3 програмного забезпечення.
| Член команди | Версія 3 Дані (годин використання за 1 місяць) | Середнє | |||||||
| Ти, Читач | 14 | 13 | 8 | 4 | 8 | 21 | 3 | 11 | 10.25 |
| Кір | 0 | 3 | 2 | 3 | 5 | 4 | 8 | 11 | 4.5 |
| Бетті | 8 | 5 | 5 | 4 | 5 | 0 | 1 | 16 | 5.5 |
| Радість | 7 | 5 | 8 | 4 | 7 | 13 | 7 | 6 | 7.125 |
| Керісса | 8 | 6 | 14 | 3 | 11 | 2 | 5 | 8 | 7.125 |
| Кристал | 6 | 7 | 4 | 7 | 6 | 3 | 7 | 5 | 5.625 |
| Марцин | 7 | 7 | 6 | 1 | 2 | 7 | 5 | 5 | 5 |
| Тиса | 3 | 3 | 5 | 4 | 14 | 13 | 3 | 2 | 5.875 |
| Тайлер | 0 | 7 | 2 | 7 | 4 | 2 | 5 | 2 | 3.625 |
| Патрік | 8 | 3 | 1 | 14 | 2 | 6 | 7 | 2 | 5.375 |
Гістограма праворуч містить дані окремих користувачів. Це показує, що приблизно половина даних (42 з 80) нижче 6, а решта вище 6.
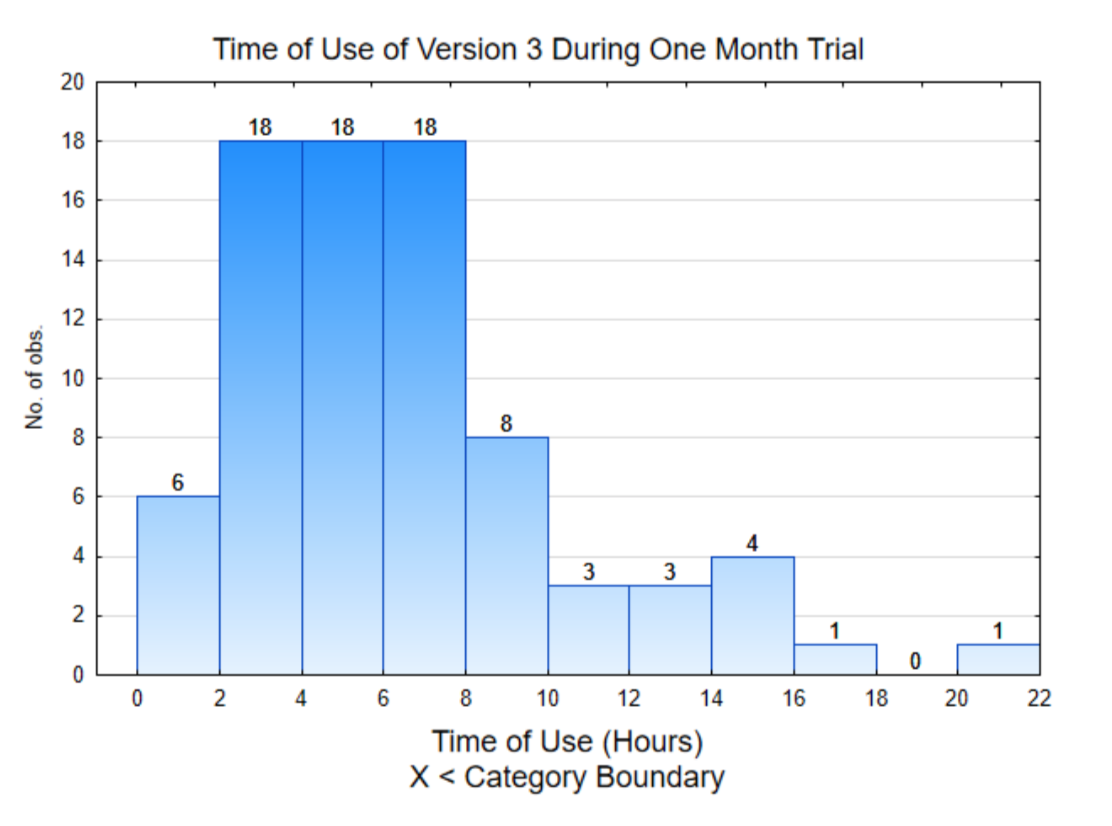
Гістограма праворуч - це середнє значення 8 користувачів для кожного члена команди. Цей розподіл вибірки показує, що 7 із 10 вибіркових засобів нижче 6.
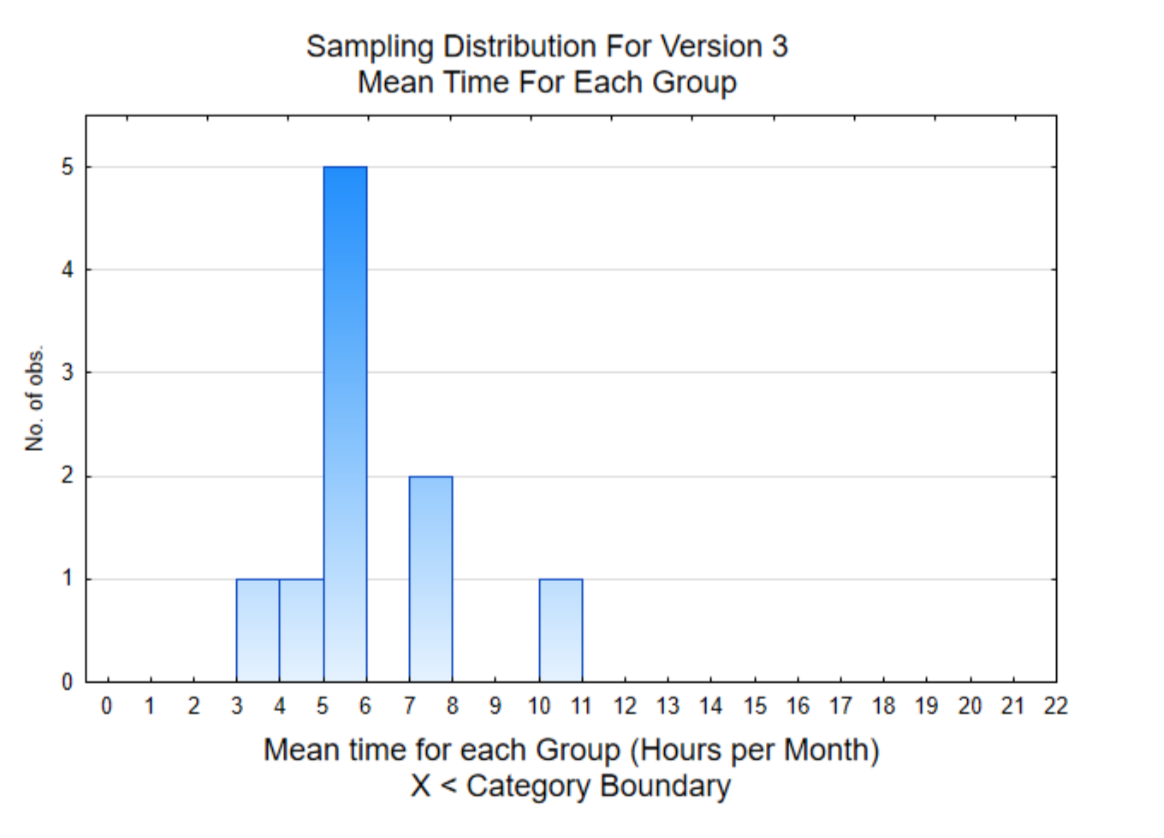
Середнє значення всіх індивідуальних значень даних - 6,0. Отже, якби ви прийшли до висновку, що версія 3 була кращою за версію 1, оскільки середнє значення ваших 8 користувачів становило 10.25 годин, ви б прийшли до неправильного висновку. Ви були б введені в оману даними, які були обрані чисто випадково.
Жодна з перших 3 версій не була особливо успішною, але ваша команда не впадає у відчай. Вони вже мають нові ідеї і складають ще одну версію своєї програми грамотності.
Версія 4.
Коли версія 4 завершена, кожен член команди випадковим чином вибирає 8 людей з низьким рівнем грамотності, як це було зроблено для попередніх версій. Дані, які записуються, - це кількість часу використання програми протягом місяця. Ваші дані наведені нижче.
| Член команди | Версія 4 Дані (годин використання за 1 місяць) | Середнє | ||||||
| Ти, Читач | 60 | 44 | 37 | 62 | 32 | 88 | 32 | 48.375 |
Виходячи з ваших результатів, чи вважаєте ви, що ця версія краще, ніж версія 1?
Так Версія 4 краще, ніж версія 1 Ні, Версія 4 не краще, ніж версія 1
Результати всіх 80 учасників наведені в таблиці нижче.
| Член команди | Версія 4 Дані (годин використання за 1 місяць) | Середнє | |||||||
| Ти, Читач | 60 | 44 | 37 | 32 | 62 | 32 | 88 | 32 | 48.375 |
| Кір | 48 | 37 | 24 | 20 | 82 | 76 | 67 | 67 | 52.625 |
| Бетті | 88 | 39 | 67 | 24 | 71 | 85 | 81 | 24 | 59,875 |
| Радість | 23 | 58 | 21 | 88 | 81 | 75 | 84 | 81 | 63.875 |
| Керісса | 88 | 24 | 58 | 53 | 81 | 57 | 88 | 24 | 59,125 |
| Кристал | 47 | 85 | 767 | 24 | 39 | 67 | 40 | 77 | 56.875 |
| Марцин | 61 | 45 | 75 | 58 | 87 | 51 | 37 | 73 | 60.875 |
| Тиса | 76 | 77 | 58 | 84 | 20 | 55 | 81 | 82 | 66.625 |
| Тайлер | 82 | 47 | 48 | 60 | 88 | 21 | 50 | 24 | 52.5 |
| Патрік | 20 | 40 | 52 | 24 | 55 | 33 | 33 | 84 | 42.625 |
Гістограма праворуч містить дані окремих користувачів. Зверніть увагу, що всі ці значення вище 20. 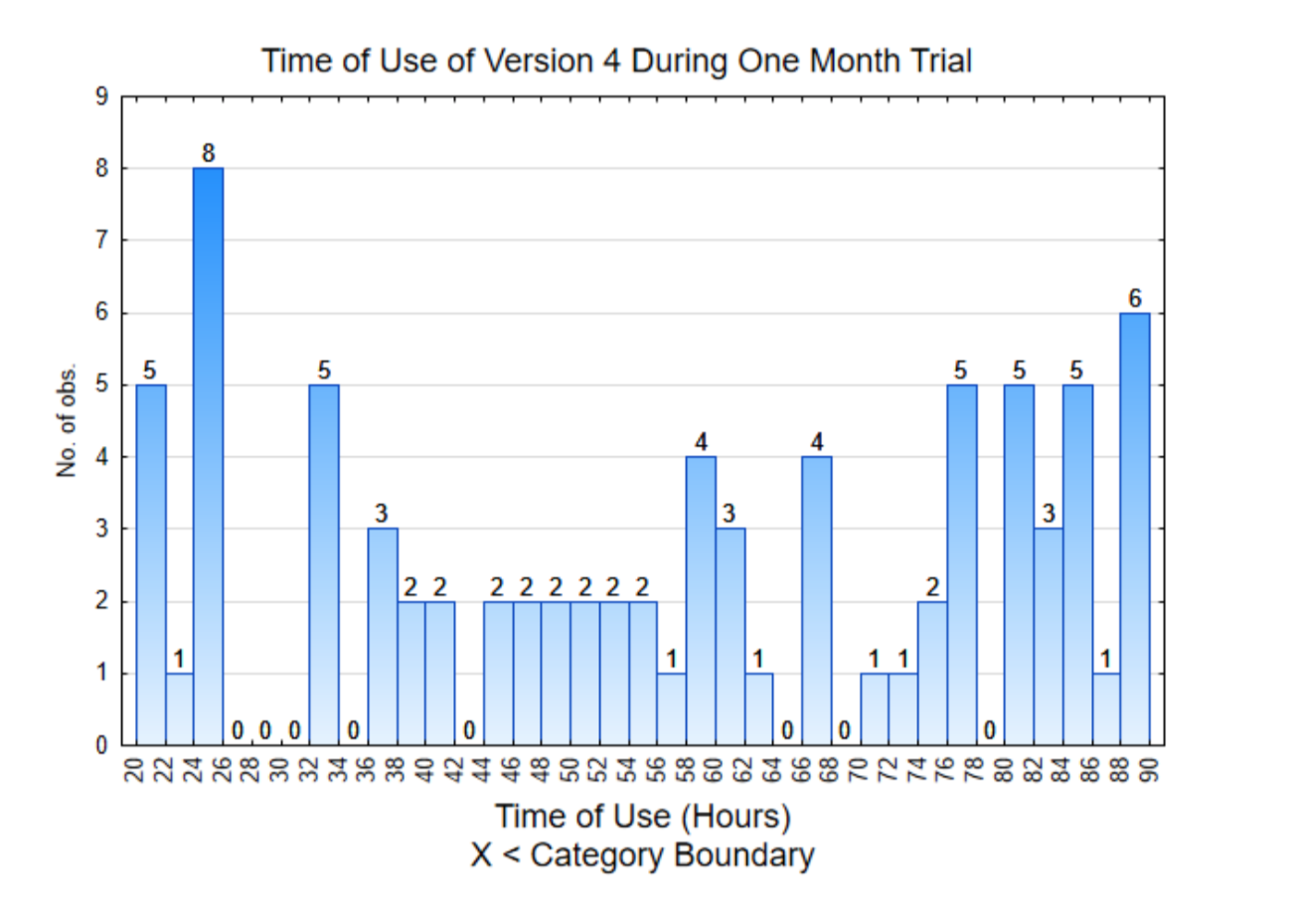
Гістограма праворуч - це середнє значення 8 користувачів для кожного члена команди. Зверніть увагу, що всі кошти зразка значно вище 6.
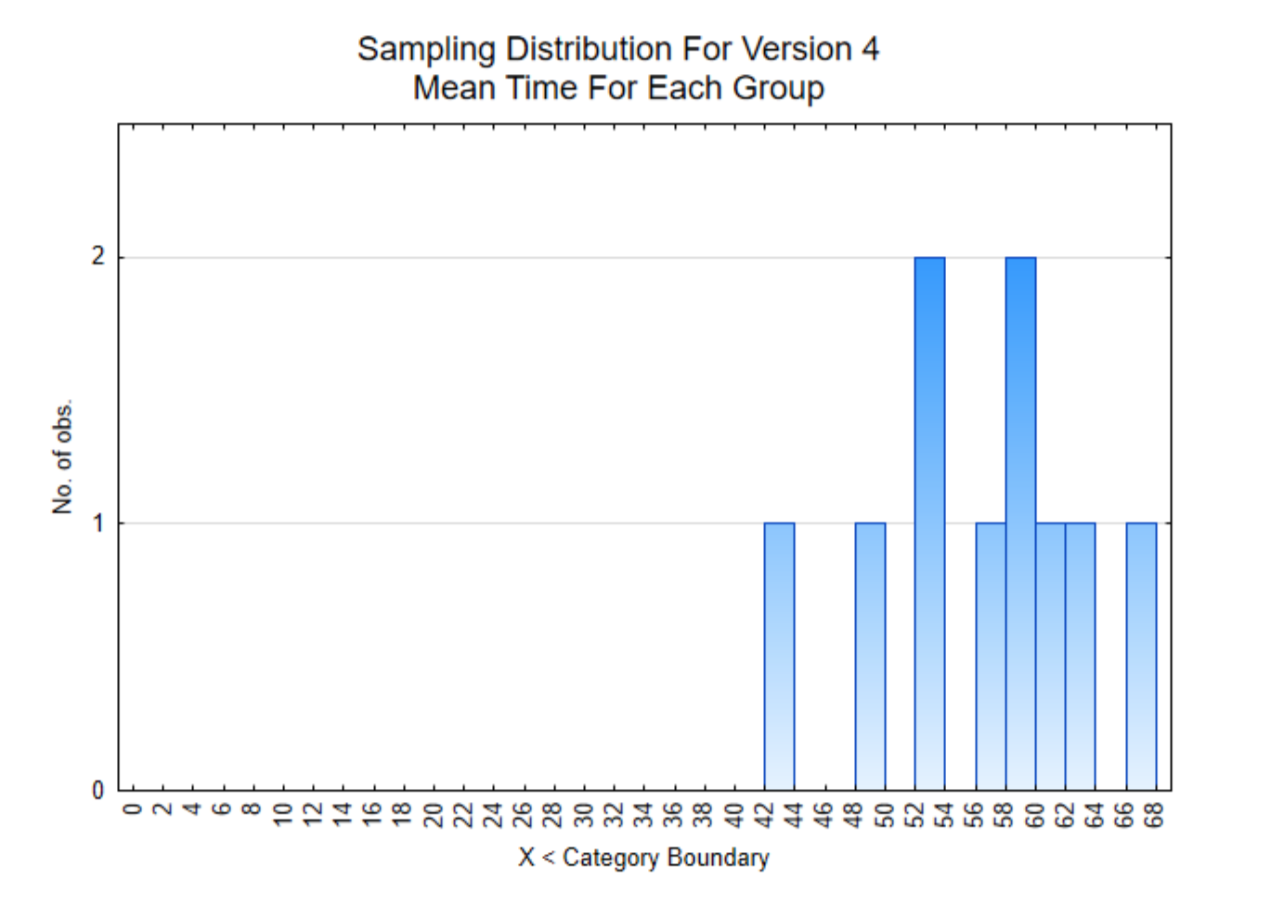
Виходячи з результатів версії 4, всі дані значно перевищують 6 годин на місяць. Середній показник становить 56,3 години на місяць, що становить майже 2 години на день. Це значно більше використання програми, ніж ранні версії, і, отже, буде додатком, який використовується в конкурсі XPrize.
Прийняття рішень за допомогою статистики
Було кілька цілей історії, яку ви щойно прочитали.
- Щоб дати вам оцінку варіації, яка може існувати у вибіркових даних.
- Щоб познайомити вас з типом графіка даних, який називається гістограма, який є хорошим способом для перегляду розподілу даних.
- Познайомити вас з концепцією розподілу вибірки, яка є розподілом засобів вибірки, а не вихідних даних.
- Щоб проілюструвати різні результати, які можуть виникнути, коли ми намагаємося відповісти на питання, використовуючи дані. Ці результати підсумовані нижче у відповідь на питання про те, чи краще нова версія, ніж перша версія.
a Версія 2: Це було не краще. Насправді, виявилося, гірше.
b Версія 3: Спочатку це виглядало краще, але в кінцевому підсумку це було те ж саме.
c Версія 4: Це було набагато краще.
Оскільки дані іноді дають чіткість щодо рішення, яке слід прийняти (Версії 2 та 4), але інші часи незрозумілі (Версія 3), у цьому розділі буде пояснено більш формальний, статистичний процес міркування з деталями, що розробляються протягом решти книги.
Перш ніж почати цей процес, необхідно чітко зрозуміти роль статистики в тому, щоб допомогти нам зрозуміти наш світ. Є два основних способи, за допомогою яких ми встановлюємо впевненість у своїх знаннях світу, надаючи аналітичні докази або емпіричні докази.
Аналітичні докази використовують визначення або математичні правила. Математичне доказ - це аналітичний метод використання встановлених фактів для доведення чогось нового. Аналітичні докази корисні для доведення речей, які є детермінованими. Детермінований означає, що один і той же результат буде досягнутий кожен раз (якщо помилки не зроблені). Алгебра та обчислення є прикладами детермінованої математики, і вони можуть бути використані для надання аналітичних доказів.
Навпаки, емпіричні дані базуються на спостереженнях. Більш конкретно, хтось запропонує теорію, а потім можна провести дослідження, щоб визначити обґрунтованість цієї теорії. Більшість ідей, які ми віримо з упевненістю, призвели до відмови від теорій, які ми раніше мали, і наші нинішні знання складаються з тих ідей, які ми не змогли відкинути за допомогою емпіричних доказів. Емпіричні докази отримані завдяки ретельним дослідженням. Це контрастує з анекдотичними доказами, які також отримують шляхом спостереження, але не суворо. Анекдотичні докази можуть вводити в оману.
Роль статистики полягає в об'єктивній оцінці доказів, щоб можна було прийняти рішення про те, відхиляти чи не відхиляти теорію. Це особливо корисно для тих ситуацій, в яких докази є результатом вибірки, взятої з набагато більшої кількості населення. На відміну від детермінованих відносин, стохастичні популяції - це ті, в яких є випадковість, тоді як докази отримані шляхом випадкової вибірки, тобто докази, які ми бачимо, є результатом випадковості.
Науковий метод, який використовується у всьому дослідницькому співтоваристві для підвищення нашого розуміння світу, заснований на пропонуванні, а потім тестуванні теорій за допомогою емпіричних методів. Статистика відіграє життєво важливу роль, допомагаючи дослідникам зрозуміти дані, які вони виробляють. Науковий метод містить наступні компоненти.
- Задати питання
- Запропонуйте гіпотезу про відповідь на питання
- Проектні дослідження (Глава 2)
- Збір даних (Глава 2)
- Розвивати розуміння даних за допомогою графіків та статистики (Глава 3)
- Використовуйте дані, щоб визначити, чи підтримує вона або суперечить гіпотезі (Розділи 5,7,8)
- Зробіть висновок.
Перш ніж досліджувати статистичні інструменти, що використовуються в науковому методі, корисно зрозуміти проблеми, з якими ми стикаємося зі стохастичними популяціями, та процес статистичного міркування, який ми використовуємо для висновків.
- Коли пропонується теорія про населення, вона базується на кожній людині чи елементі населення. Населення - це весь набір людей або речей, що представляють інтерес.
- Оскільки населення містить занадто багато людей або елементів, з яких можна отримати інформацію, ми робимо гіпотезу про те, якою була б інформація, якби ми могли її отримати.
- Докази збираються шляхом взяття проби у населення.
- Докази використовуються для визначення того, чи слід відкидати гіпотезу чи не відхиляти.
Ці чотири складові процесу статистичного міркування тепер будуть розроблені більш повно. Завдання полягає в тому, щоб визначити, чи є достатня підтримка гіпотези на основі часткових доказів, коли відомо, що часткові докази змінюються залежно від обраного зразка. За аналогією, це все одно, що намагатися знайти потрібну людину, щоб одружитися, отримуючи часткові докази від знайомства або знайти потрібну людину для найму, отримуючи часткові докази від інтерв'ю.
1. Теорії про популяції.
Коли хтось має теорію, ця теорія застосовується до населення, яке повинно бути чітко визначено. Наприклад, населення може бути кожен в країні, або всі люди похилого віку, або всі в політичній партії, або кожен, хто спортивний, або кожен, хто є двомовним, і т.д. населення також може бути будь-якою частиною природного світу, включаючи тварин, рослини, хімікати, вода і т.д. теорії, які можуть бути дійсними для одного населення не обов'язково дійсні для іншого. Приклади теорій, що застосовуються до популяції, включають наступне.
- Команда, що працює над програмою для грамотності, стверджує, що одна версія їхнього додатка буде регулярно використовуватися всім населенням дорослих з низькими навичками грамотності, які мають до неї доступ.
- Педагог теоретизує, що її педагогіка викладання призведе до найбільшого рівня успіху для всього населення всіх учнів, яких вона буде навчати.
- Фармацевтична компанія припускає, що нові ліки будуть ефективними при лікуванні всього населення людей, які страждають від захворювання, які використовують ліки.
- Вчений з водних ресурсів теоретизує, що рівень забруднення всього водойми знаходиться на небезпечному рівні.
1.5 Дані, параметри та статистика
Перш ніж обговорювати гіпотези, необхідно поговорити про дані, параметрах і статистиці.
На найбільшому рівні виділяють два типи даних, категоричні і кількісні. Категоричні дані - це дані, які можна розставити в категорії. Приклади включають відповіді так/ні, або такі категорії, як колір, релігія, національність, прохід/невдача, виграш/програш і т.д. кількісні дані - це дані, які складаються з чисел, отриманих в результаті підрахунків або вимірювань. Приклади включають, зріст, вага, час, кількість грошей, кількість злочинів, частота серцевих скорочень тощо.
Способи, якими ми розуміємо дані, графіки та статистику, залежать від типу даних. Статистика - це цифри, які використовуються для узагальнення даних. На даний момент є дві статистичні дані, які будуть важливими, пропорції і засоби. Пізніше в книзі будуть введені інші статистичні дані.
Пропорція - це частина, розділена на ціле. Він схожий на відсоток, але не множиться на 100. Частина - це кількість значень даних у категорії. Ціле - це кількість значень даних, які були зібрані. Таким чином, якби 800 людей запитали, чи відвідували вони коли-небудь чужу країну, а 200 сказали, що вони мали, то частка людей, які відвідали чужу країну, становила б:
\(\dfrac{\text{part}}{\text{whole}} = \dfrac{x}{n} = \dfrac{200}{800} = 0.25\)
Частина представлена змінною x, а ціле - змінною n.
Середнє значення, часто відоме як середнє значення, - це сума кількісних даних, поділена на кількість значень даних. Якщо ми повернемося до програми для грамотності, версія 3, дані для Марчіна були:
| Марцин | 7 | 7 | 6 | 1 | 2 | 7 | 5 | 5 | 5 |
Середнє значення є\(\dfrac{7+ 7 + 6 + 1 + 2 + 7 + 5 +}{8} = \dfrac{40}{8} = 5\)
Хоча статистика - це цифри, які використовуються для узагальнення вибіркових даних, параметри - це цифри, які використовуються для узагальнення всіх даних у популяції. Щоб знайти параметр, однак, потрібно отримати дані від кожної людини або елемента в популяції. Це називається переписом. Взагалі, це занадто дорого, займає занадто багато часу або просто неможливо провести перепис. Однак, оскільки наша теорія стосується популяції, то ми повинні розрізняти параметри і статистику. Для цього використовуємо різні змінні.
| Тип даних | Резюме | Населення | Зразок |
| Категоричний | Пропорція | р | \(\hat{p}\)(р-капелюх) |
| Кількісні | Середнє | \(\mu\) | \(bar{x}\)(Х-бар) |
Для деталізації, коли дані категоричні, частка всієї сукупності представлена змінною p, тоді як частка вибірки представлена змінною\(\hat{p}\). Коли дані кількісні, середнє значення всього населення представлено грецькою літерою\(\mu\), тоді як середнє значення вибірки представлено змінною\(bar{x}\).
У типовій ситуації ми не будемо знати ні р, ні\(\mu\) і тому ми б зробили гіпотезу про них. З даних, які ми збираємо, ми знайдемо\(\hat{p}\) або\(bar{x}\) використаємо їх, щоб визначити, чи слід відкидати нашу гіпотезу.
2. Гіпотези
Про параметри пишуться гіпотези до збору даних (апріорі). Гіпотези записуються парами, які містять нульову гіпотезу (\(H_0\)) і альтернативну гіпотезу (\(H_1\)).
Припустимо, хтось мав теорію про те, що частка людей, які відвідали спортивну подію в прямому ефірі за останній рік, була більшою за 0,2. У такому випадку вони писали б свої гіпотези як:
\(H_0\):\(p = 0.2\)
\(H_1\):\(p > 0.2\)
Якби у когось була теорія про те, що середні години перегляду спортивних подій по телевізору становили менше 15 годин на тиждень, то вони написали б свої гіпотези так:
\(H_0\):\(\mu\) = 15
\(H_1\):\(\mu\) < 15
Правила, які використовуються для написання гіпотез, такі:
- Завжди є дві гіпотези, нульова і альтернативна.
- Обидві гіпотези мають приблизно один і той же параметр.
- Нульова гіпотеза завжди містить знак рівності (=).
- Альтернатива містить знак нерівності (<, >, ≠).
- Число буде однаковим для обох гіпотез.
Коли гіпотези використовуються для прийняття рішень, їх слід підбирати таким чином, щоб, якщо докази підтверджують нульову гіпотезу, повинно бути прийнято одне рішення, а докази, що підтверджують альтернативну гіпотезу, повинні привести до іншого рішення.
Гіпотеза, яку бажають дослідники, часто є альтернативною гіпотезою. Гіпотеза, яка буде перевірена, - це нульова гіпотеза. Якщо нульова гіпотеза відхилена через доказів, то приймається альтернативна гіпотеза. Якщо докази не призводять до відхилення нульової гіпотези, ми не можемо зробити висновок, що нуль є істинним, лише те, що він не був відхилений. У цьому тексті ми будемо використовувати термін «підтримується». Таким чином, або нульова гіпотеза підтримується даними, або підтримується альтернативна гіпотеза. Підтвердження даних не означає, що гіпотеза є правдивою, а скоріше, що рішення, яке ми приймаємо, має базуватися на гіпотезі, яка підтримується.
Дві ситуації, з якими ви зіткнетеся в цьому тексті, - це коли існує теорія про пропорцію або середнє значення для однієї популяції або коли існує теорія про те, як пропорція або середнє значення порівнюються між двома популяціями. Вони зведені в таблиці нижче.
|
Гіпотеза про одну популяції |
Позначення |
Гіпотеза про 2 популяції |
Позначення |
|
Пропорція більше 0,2 |
\(H_0\):\(p = 0.2\) |
Частка населення А більша, ніж частка населення В |
\(H_0\):\(p_A = p_B\) |
|
Пропорція менше 0,2 |
\(H_0\):\(p = 0.2\) |
Частка населення А менше, ніж частка населення В |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A < p_B\) |
|
Пропорція не дорівнює 0,2 |
\(H_0\):\(p = 0.2\) |
Частка населення А відрізняється від частки населення В |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A \ne p_B\) |
|
Середнє значення більше 15 |
\(H_0\):\(\mu = 15\) |
Середнє значення чисельності населення А більше, ніж середнє значення популяції В |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A > \mu_B\) |
|
Середнє значення менше 15 |
\(H_0\):\(\mu = 15\) \(H_1\):\(\mu < 15\) |
Середнє значення чисельності населення А менше, ніж середнє значення популяції В |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A < \mu_B\) |
|
Середнє значення не дорівнює 15 |
\(H_0\):\(\mu = 15\) \(H_1\):\(\mu \ne 15\) |
Середнє значення чисельності населення А відрізняється від середнього показника чисельності населення В |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A \ne \mu_B\) |
3. Використовуючи докази, щоб визначити, яка гіпотеза, швидше за все, вірна.
З історії програми «Грамотність» ви повинні були бачити, що іноді докази чітко підтверджують один висновок (наприклад, версія 2 гірша за версію 1), іноді вона чітко підтримує інший висновок (версія 4 краще, ніж версія 1), а іноді це занадто важко сказати (версія 3). Перш ніж обговорювати більш формальний спосіб перевірки гіпотез, давайте розвинемо деяку інтуїцію щодо гіпотез і доказів.
Припустимо, гіпотези
\(H_0\): р = 0,4
\(H_0\): р < 0,4
Якщо докази з зразка є\(\hat{p} = 0.45\), чи підтверджують ці докази нульові або альтернативні? Вирішіть, перш ніж продовжувати.
Гіпотези містять знак рівності і знак менше, але не більше знака, тому коли докази більше, ніж, який висновок слід зробити? Оскільки пропорція вибірки не підтримує альтернативну гіпотезу, оскільки вона не менше 0,4, то ми зробимо висновок, що 0.45 підтримує нульову гіпотезу.
Якщо докази зразка\(\hat{p}\) = 0,12, чи підтвердили б ці докази нульові або альтернативні? Вирішіть, перш ніж продовжувати.
У цьому випадку 0,12 значно менше 0,4, тому підтримує альтернативу.
Якщо докази зразка\(\hat{p}\) = 0,38, чи підтвердили б ці докази нульові або альтернативні? Вирішіть, перш ніж продовжувати.
Це ситуація, яку визначити складніше. Хоча ви, можливо, вирішили, що 0.38 менше 0.4 і тому підтримує альтернативу, швидше за все, він підтримує нульову гіпотезу.
Як це може бути?
В арифметиці 0,38 завжди менше 0,4. Однак в статистиці це не обов'язково так. Причина в тому, що гіпотеза йде про якийсь параметр, мова йде про всю сукупність. З іншого боку, докази є зі зразка. Різні зразки дають різні результати. Пряме порівняння статистики (0,38) з гіпотезованим параметром (0,4) недоцільно. Швидше, нам потрібен інший спосіб зробити це визначення. Перш ніж зупинитися на іншому шляху, давайте спробуємо ще один.
Припустимо, гіпотези
\(H_0\):\(\mu = 30\)
\(H_1\):\(\mu > 30\)
Якщо докази з вибірки\(\bar{x}\) = 80, яка гіпотеза підтримується? Нульова альтернатива
Якщо докази з вибірки\(\bar{x}\) = 26, яка гіпотеза підтримується? Нульова альтернатива
Якщо докази з вибірки\(\bar{x}\) = 32, яка гіпотеза підтримується? Нульова альтернатива
Якщо докази\(\bar{x}\) = 80, альтернатива буде підтримана. Якщо докази\(\bar{x}\) = 26, нуль буде підтримуватися. Якщо докази\(\bar{x}\) = 32, на перший погляд, це, здається, підтримує альтернативу, але вона близька до гіпотези, тому ми зробимо висновок, що ми не впевнені, що вона підтримує.
Можливо, вас бентежить неможливість зробити чіткий висновок з доказів. Адже як люди можуть приймати рішення? Далі наведено пояснення стратегії статистичного міркування, яка використовується.
Статистичний процес міркування
Процес міркування для вирішення того, яку гіпотезу підтримують дані, однаковий для будь-якого параметра (p або μ).
- Припустимо, що нульова гіпотеза вірна.
- Зберіть дані та розрахуйте статистику.
- Визначте ймовірність вибору даних, які виробляли статистику або могли б створити більш екстремальну статистику, припускаючи, що нульова гіпотеза вірна.
- Якщо дані ймовірні, вони підтримують нульову гіпотезу. Однак, якщо вони малоймовірні, вони підтримують альтернативну гіпотезу.
Щоб проілюструвати це, ми використаємо інше дослідницьке запитання: «Яка частка дорослих американців вважає, що ми повинні перейти до суспільства, яке більше не використовує викопне паливо (вугілля, нафта, природний газ)? Припустимо, у дослідника є теорія, що частка дорослих американців, які вважають, що ми повинні зробити цей перехід, перевищує 0,6. Гіпотези, які будуть використані для цього:
\(H_0\): р = 0,6
\(H_1\): р > 0,6
Ми могли б візуалізувати цю ситуацію, якби використали мішок з мармуром. Оскільки перший крок у процесі статистичного міркування полягає в тому, щоб припустити, що нульова гіпотеза вірна, то наш мішок мармуру може містити 6 зелених кульок, які представляють дорослих, які хочуть припинити використання викопного палива, і 4 білих мармуру, щоб представляти тих, хто хоче продовжувати використовувати викопне паливо. Відбір проб буде проводитися з заміною, а це означає, що після того, як мармур буде підібраний, колір записується і мармур поміщається назад в мішок.
Якщо з мішка вибрано 100 кульок (із заміною), чи очікуєте ви, що рівно 60 з них (60%) будуть зеленими? Це траплялося б кожного разу?
Результати комп'ютерного моделювання цього процесу відбору проб наведені нижче. Моделювання складається з 100 кульок вибирається, при цьому процес повторюється 20 разів.
| 0,62 | 0,57 | 0,58 | 0,64 | 0,64 | 0,53 | 0,73 | 0,55 | 0,58 | 0,55 |
| 0,61 | 0.66 | 0.6 | 0,54 | 0,54 | 0.5 | 0,62 | 0,55 | 0,61 | 0,61 |
Зверніть увагу, що в деяких випадках частка вибірки перевищує 0,6, в деяких випадках вона менше 0,6 і є лише один раз, коли вона фактично дорівнювала 0,6. З цього ми можемо зробити висновок, що хоча нульова гіпотеза дійсно була правдою, є пропорції вибірки, які можуть змусити нас думати, що альтернатива є істинною (що може призвести до помилки).
У процесі статистичного міркування є три пункти, які потребують уточнення. Перший полягає у визначенні того, які значення ймовірні або малоймовірні, тоді як другий - визначити точку поділу між ймовірним і малоймовірним. Третій момент уточнення - напрямок крайнього.
Ймовірні та малоймовірні значення
Коли докази збираються шляхом взяття випадкової вибірки з популяції, випадкова вибірка, яка фактично відібрана, є лише однією з багатьох, багатьох, багатьох можливих зразків, які могли бути взяті замість цього. Кожен випадковий зразок дасть різну статистику. Якби ви могли побачити всю статистику, ви могли б визначити, чи був зразок, який ви взяли, вірогідним чи малоймовірним. Графік статистики, такий як пропорції вибірки або засоби вибірки, називається розподілом вибірки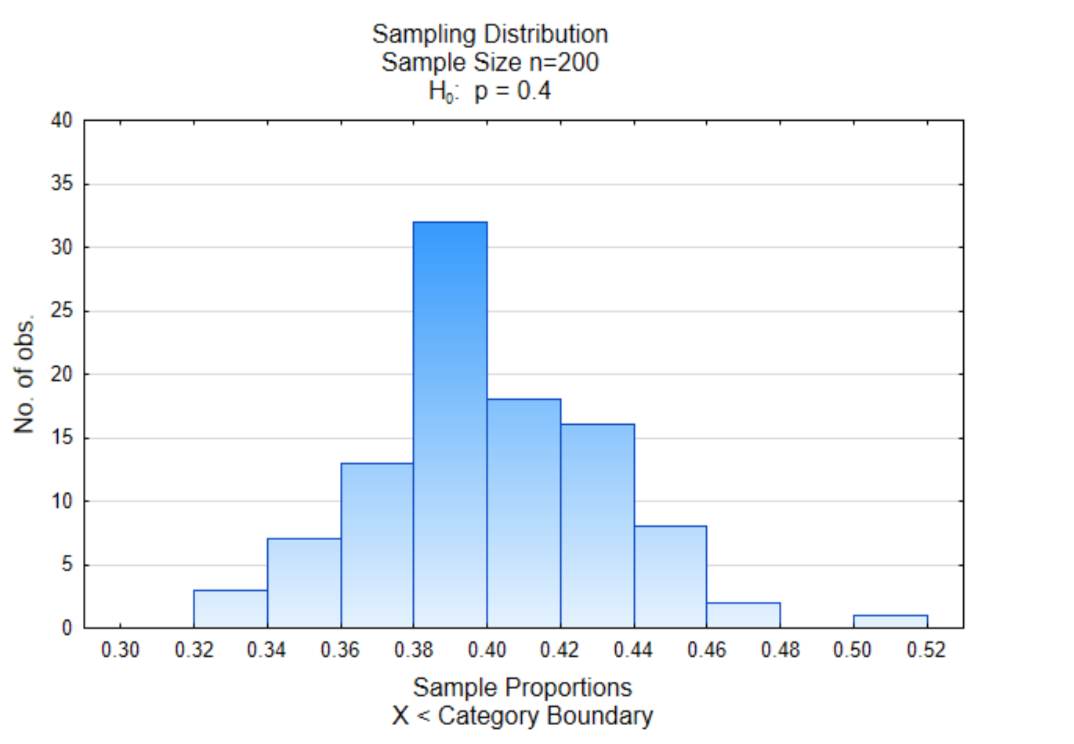 .
.
Хоча не має сенсу брати багато різних зразків, щоб знайти всю можливу статистику, кілька демонстрацій того, що станеться, якщо хтось зробить, це може дати вам певну впевненість, що подібні результати будуть відбуватися і в інших ситуаціях. Дані, використані на графіках нижче, були зроблені за допомогою комп'ютерного моделювання.
Гістограма праворуч - це розподіл вибірки пропорцій вибірки. 100 різних зразків, які містили 200 значень даних, були відібрані з популяції, в якій 40% сприяли заміні викопного палива (зеленого мармуру). Пропорція на користь заміни викопного палива (зеленого мармуру) була знайдена для кожного зразка та графізована. Є дві речі, які ви повинні помітити на графіку. Перший полягає в тому, що більшість пропорцій зразка згруповані разом посередині, а друга річ полягає в тому, що середина становить приблизно 0,40, що еквівалентно частці зеленого мармуру в контейнері.
Це, звичайно, може бути збігом обставин. Отже, давайте розглянемо інший зразок. У цьому первісне населення становило 60% зеленого мармуру, що представляють тих, хто виступає за заміну викопного палива. Розмір вибірки становив 500, а процес повторювався 100 разів. 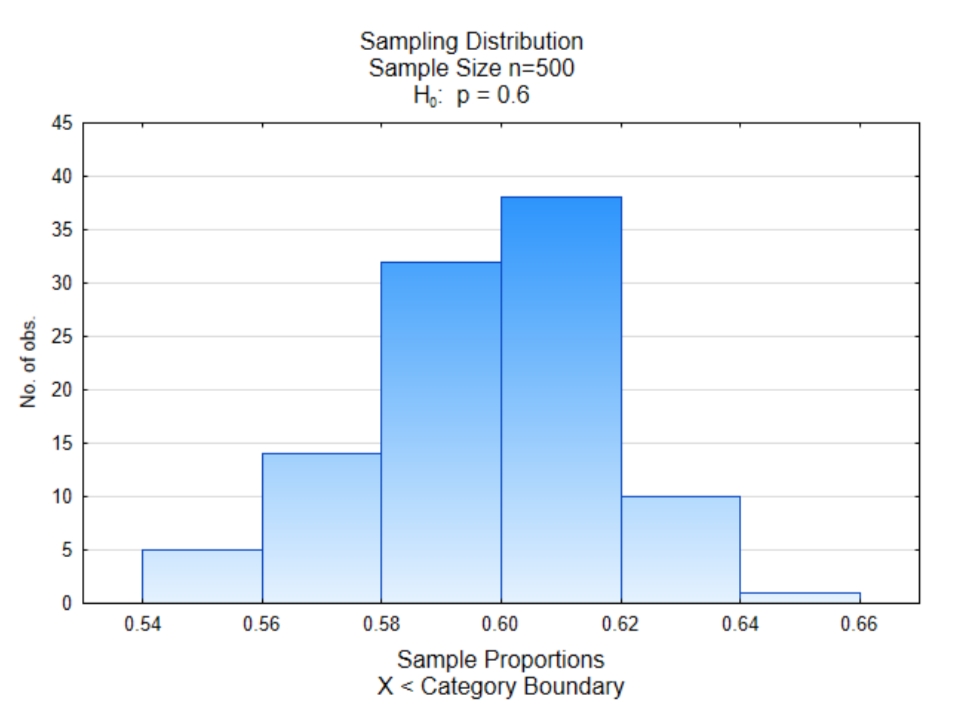
Знову ми бачимо більшість пропорцій вибірки, згрупованих посередині, а середина становить близько значення 0,60, що є часткою зеленого мармуру в початковій популяції.
Ми розглянемо ще один приклад. У цьому прикладі частка на користь заміни викопного палива становить 0,80, тоді як частка протилежних - 0,20. Розмір вибірки становитиме 1000 і буде 100 зразків такого розміру. Куди ви очікуєте падіння центру цієї дистрибуції? 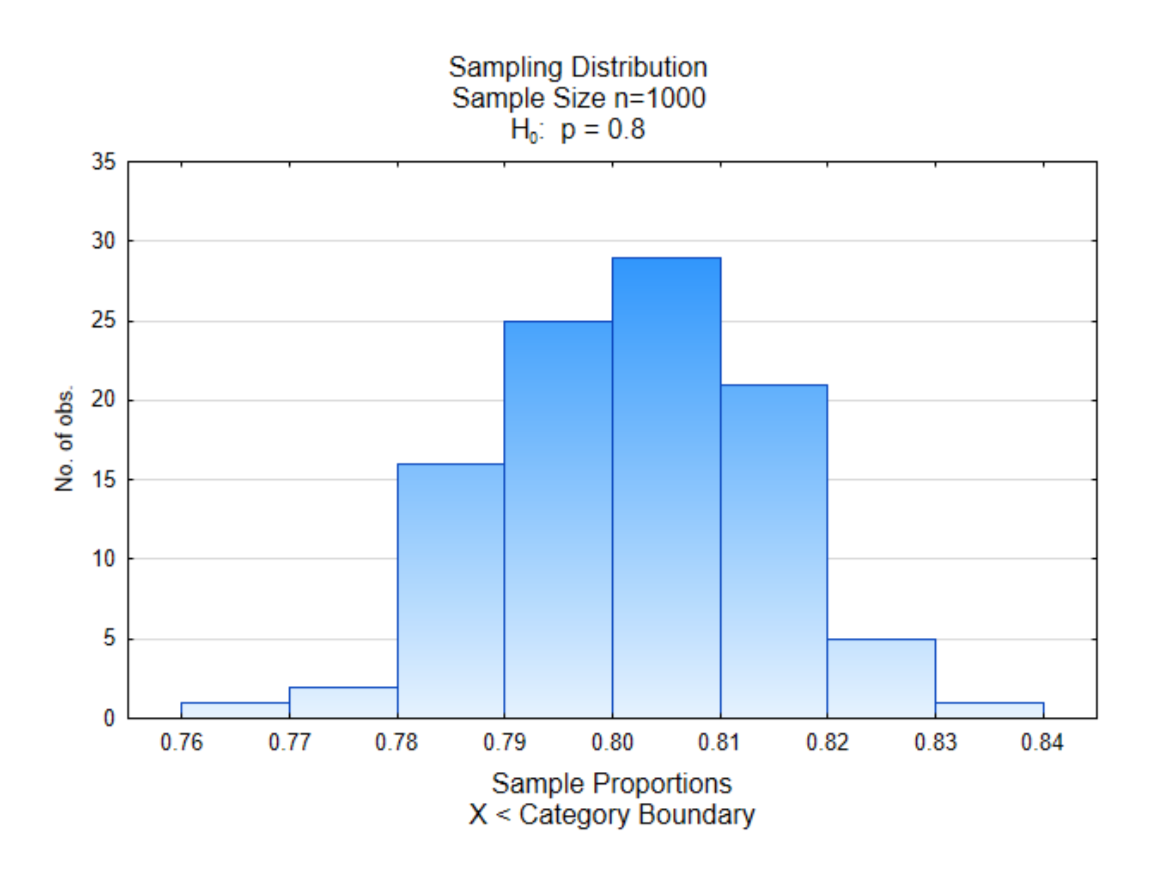
Як бачите, центр цього розподілу знаходиться близько 0,80 з більшою кількістю значень біля середини, ніж по краях.
Одне питання, яке не було вирішено, - це вплив розміру вибірки. Розміри вибірки представлені змінною n, всі ці три графіки мали різні розміри вибірки. Перший зразок мав n = 200, другий мав n = 500, а третій мав n = 1000. Щоб побачити ефект цих різних розмірів вибірки, всі три набори пропорцій зразка були позначені на одній гістограмі. 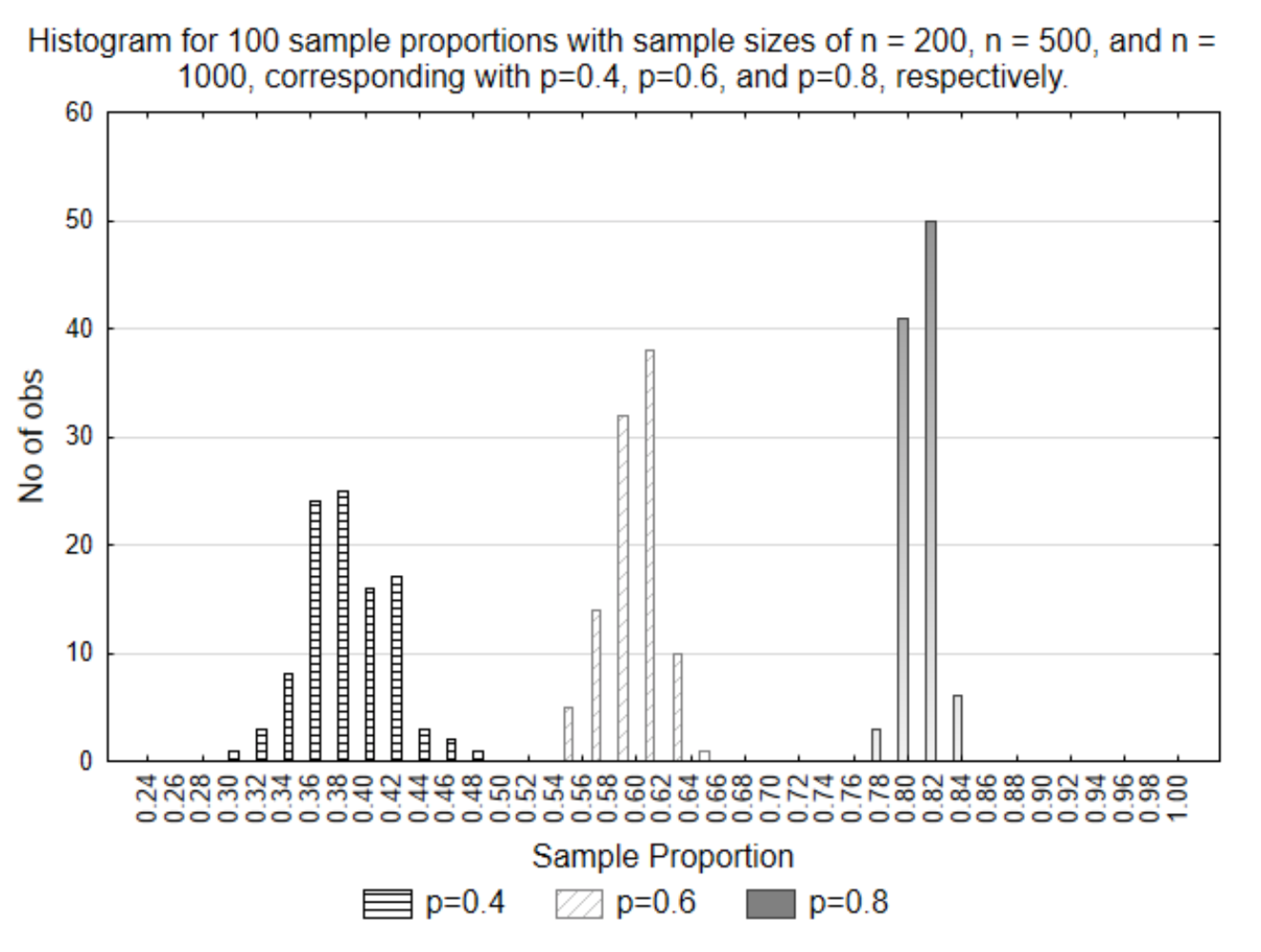
Цей графік ілюструє те, що чим менший розмір вибірки, тим більше варіацій існує в пропорціях вибірки. Це очевидно, тому що вони розкидані більше. І навпаки, чим більше розмір вибірки, тим менше варіацій існує. Це означає, що чим більше розмір вибірки, тим ближче результат вибірки буде до параметра. Чи здається це розумним? Якби в населенні було 10 000 людей, і ви отримали думку 9 999 з них, чи вважаєте ви, що всі ваші можливі пропорції вибірки були б ближче до параметра (частка населення), ніж якби ви запитували лише 20 людей?
Ми повернемося до розподілів вибірки за короткий час, але спочатку нам потрібно дізнатися про напрямки крайнощів і ймовірності.
Напрямок екстриму
Напрямок крайніх - це напрямок (ліворуч або праворуч) на числовій лінії, що змусить вас думати, що альтернативна гіпотеза вірна. Більше символів мають напрямок крайнього вправо, менше, ніж символи вказують напрямок вліво і не-рівні знаки вказують на двосторонній напрямок крайнього.
| Позначення | Позначення | Напрямок екстриму |
| \(H_0\):\(p = 0.2\) \(H_1\):\(p > 0.2\) |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A > p_B\) |
Правий |
| Ліворуч | \(H_0\):\(p_A = p_B\) \(H_1\):\(p_A < p_B\) |
Ліворуч |
| \(H_0\):\(p = 0.2\) \(H_1\):\(p \ne 0.2\) |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A \ne p_B\) |
Двостороння |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu > 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A > \mu_B\) |
Правий |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu < 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A < \mu_B\) |
Ліворуч |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu \ne 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A \ne \mu_B\) |
Двостороння |
Імовірність
В цей час необхідно провести коротку дискусію про ймовірність. Більш детальне обговорення відбудеться в розділі 4. Коли теорії перевіряються емпіричним шляхом шляхом вибірки зі стохастичної популяції, то вибірка, яка отримана, базується на випадковості. Коли вибірка вибирається випадковим процесом і обчислюється статистика, можна визначити ймовірність отримання цієї статистики або більш екстремальної статистики, якщо ми знаємо розподіл вибірки.
За визначенням ймовірність - це кількість сприятливих результатів, поділене на кількість можливих результатів.
\[P(A) = \dfrac{Number\ of\ Favorable\ Outcomes}{Number\ of\ Possible\ Outcomes}\]
Ця формула передбачає, що всі результати однаково вірогідні, як це теоретично буває у випадкових процесах відбору. Він відображає частку разів, що результат був би отриманий, якби експеримент був проведений дуже велика кількість разів. Оскільки ви не можете мати від'ємне число результатів або більш успішних результатів, ніж це можливо, ймовірність завжди дорівнює дробу або десятковій дробі від 0 до 1. Це показано узагальнено,\(0 \le P(A) \le 1\) коли P (A) представляє ймовірність події А.
Використання розподілів вибірки для перевірки гіпотез
Пам'ятайте наше дослідницьке запитання: «Яка частка дорослих американців вважає, що ми повинні перейти до суспільства, яке більше не використовує викопне паливо (вугілля, нафта, природний газ)? Теорія дослідників полягає в тому, що частка дорослих американців, які вважають, що ми повинні зробити цей перехід, перевищує 0,6. Гіпотези, які будуть використані для цього:
\(H_0 : p = 0.6\)
\(H_1 : p > 0.6\)
Щоб перевірити цю гіпотезу, нам потрібні дві речі. По-перше, нам потрібен розподіл вибірки для нульової гіпотези, оскільки ми будемо вважати, що це правда, як зазначено першим у списку для процесу міркування, використовуваного для перевірки гіпотези. Друге, що нам потрібно - це дані. Оскільки це навчально, на цьому етапі буде надано кілька пропорцій зразка, щоб ви могли порівнювати та порівнювати результати.
Невелика зміна була внесена в розподіл вибірки, який був показаний раніше. У верхній частині кожної планки знаходиться пропорція. На осі х також є пропорції. Різниця між цими пропорціями полягає в тому, що ті, що знаходяться на осі х, вказують пропорції зразка, тоді як пропорції у верхній частині брусків вказують на частку пропорцій зразка, які були між двома граничними значеннями. Так, з 100 пропорцій зразка 0,38 (або 38%) з них становили від 0,60 до 0,62. Пропорції у верхній частині брусків також можна інтерпретувати як ймовірності.
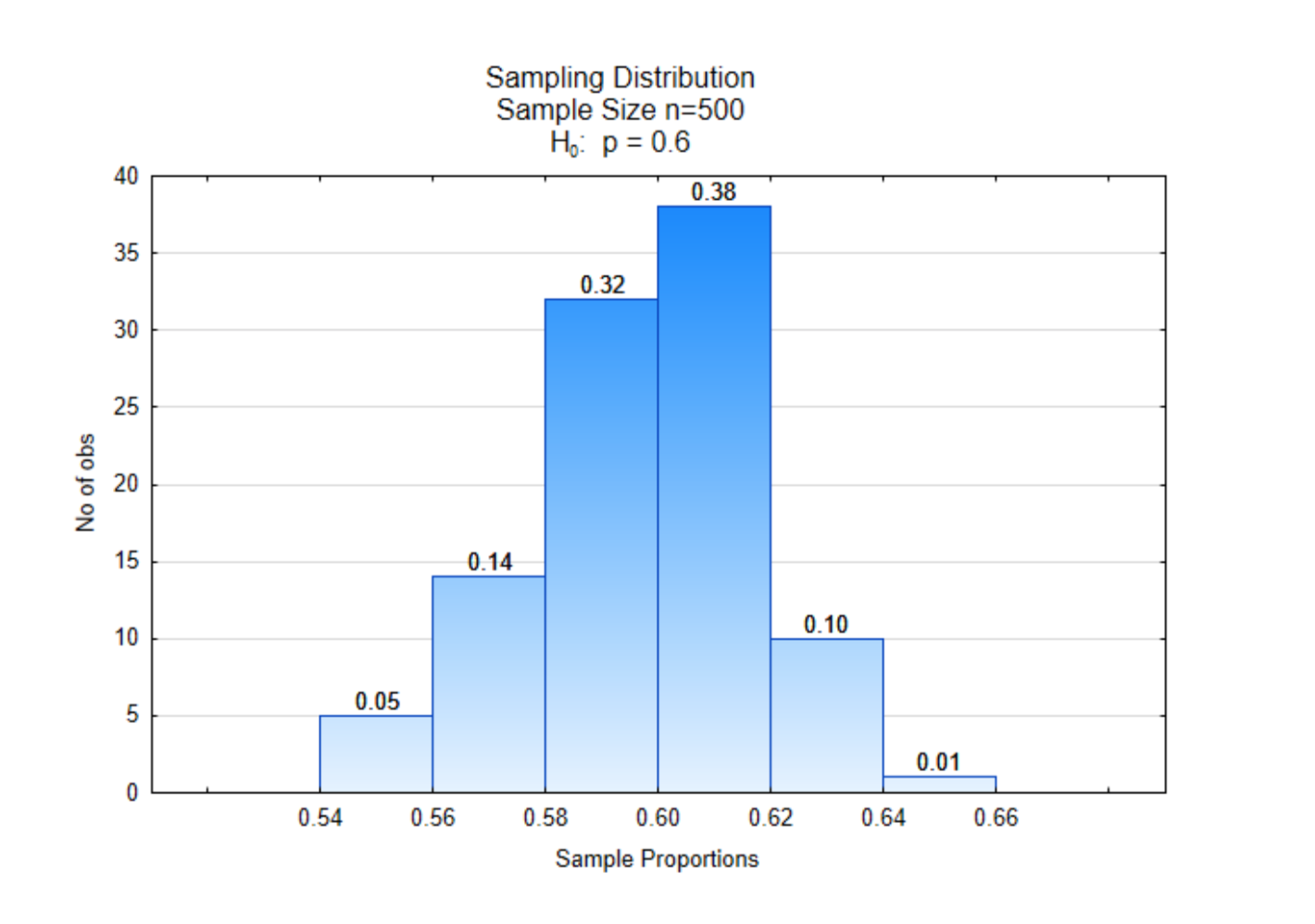
Саме за допомогою цього розподілу вибірки з нульових гіпотез ми можемо знайти ймовірність, або ймовірність отримання наших даних, або більш екстремальних даних. Цю ймовірність ми будемо називати p-значенням.
Нагадаємо, для гіпотези, яку ми перевіряємо, напрямок крайності - праворуч.
Припустимо, пропорція вибірки, яку ми отримали для наших даних,\(\hat{p}\) склала = 0,64. Яка ймовірність того, що ми отримали б цю частку вибірки або більш екстремальну від цього розподілу? Ця ймовірність дорівнює 0,01, отже, p-значення дорівнює 0,01. Це число знаходиться у верхній частині крайньої правої панелі.
Припустимо, пропорція вибірки, яку ми отримали з наших даних,\(\hat{p}\) склала = 0,62. Яка ймовірність того, що ми отримали б цю частку вибірки з цього розподілу? Ця ймовірність дорівнює 0.11. Це було розраховано шляхом додавання пропорцій у верхній частині двох крайніх правих смуг. Значення p - 0,11.
Ви спробуєте. Припустимо, пропорція вибірки, яку ми отримали з наших даних,\(\hat{p}\) склала = 0,60. Яка ймовірність того, що ми отримали б цю частку вибірки з цього розподілу?
Тепер, припустимо, частка вибірки, яку ми отримали з наших даних, була\(\hat{p}\) = 0,68. Яка ймовірність того, що ми отримали б цю частку вибірки з цього розподілу? У цьому випадку немає доказів будь-яких пропорцій вибірки, рівних 0,68 або вище, тому, отже, ймовірність або p-значення дорівнюватиме 0.
тестування гіпотези
Ми зараз спробуємо визначити, яка гіпотеза підкріплена даними. Ми будемо використовувати розподіл p=0.8 для представлення альтернативної гіпотези. Як нульовий, так і альтернативний розподіли показані на одному графіку.
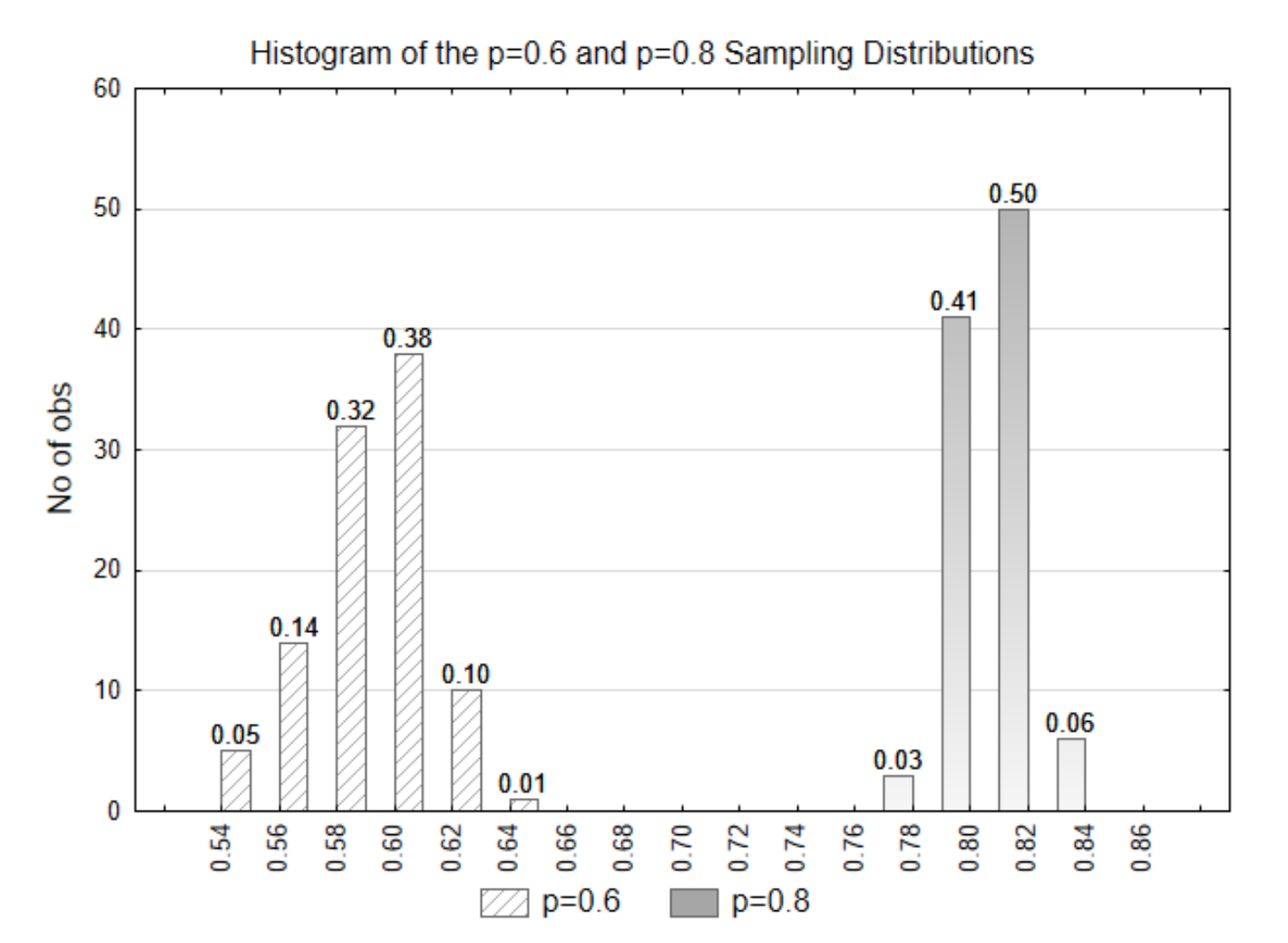
Якщо вибрані дані мали статистику\(\hat{p}\) = 0,58, що таке p-значення? Як ви думаєте, з якого з двох дистрибутивів надійшли дані? Яка гіпотеза підтримується?
Значення p - 0,81 (0,32+0,38+0,10+0,01). Ці дані надійшли з нульового дистрибутива (p=0.6). Ці докази підтверджують нульову гіпотезу.
Якщо вибрані дані були\(\hat{p}\) = 0,78, то що таке p-значення? Як ви думаєте, з якого з двох дистрибутивів надійшли дані? Яка гіпотеза підтримується?
Значення p дорівнює 0, оскільки у розподілі p=0.6 немає значень 0,78 або вище. Дані надійшли з альтернативного (p=0.8) розподілу. Альтернативна гіпотеза підтримується.
У попередніх прикладах існує чітке розмежування між нульовим та альтернативним розподілами. У наступному прикладі відмінність не настільки зрозуміла. Альтернативний розподіл буде представлений з пропорцією 0,65
. 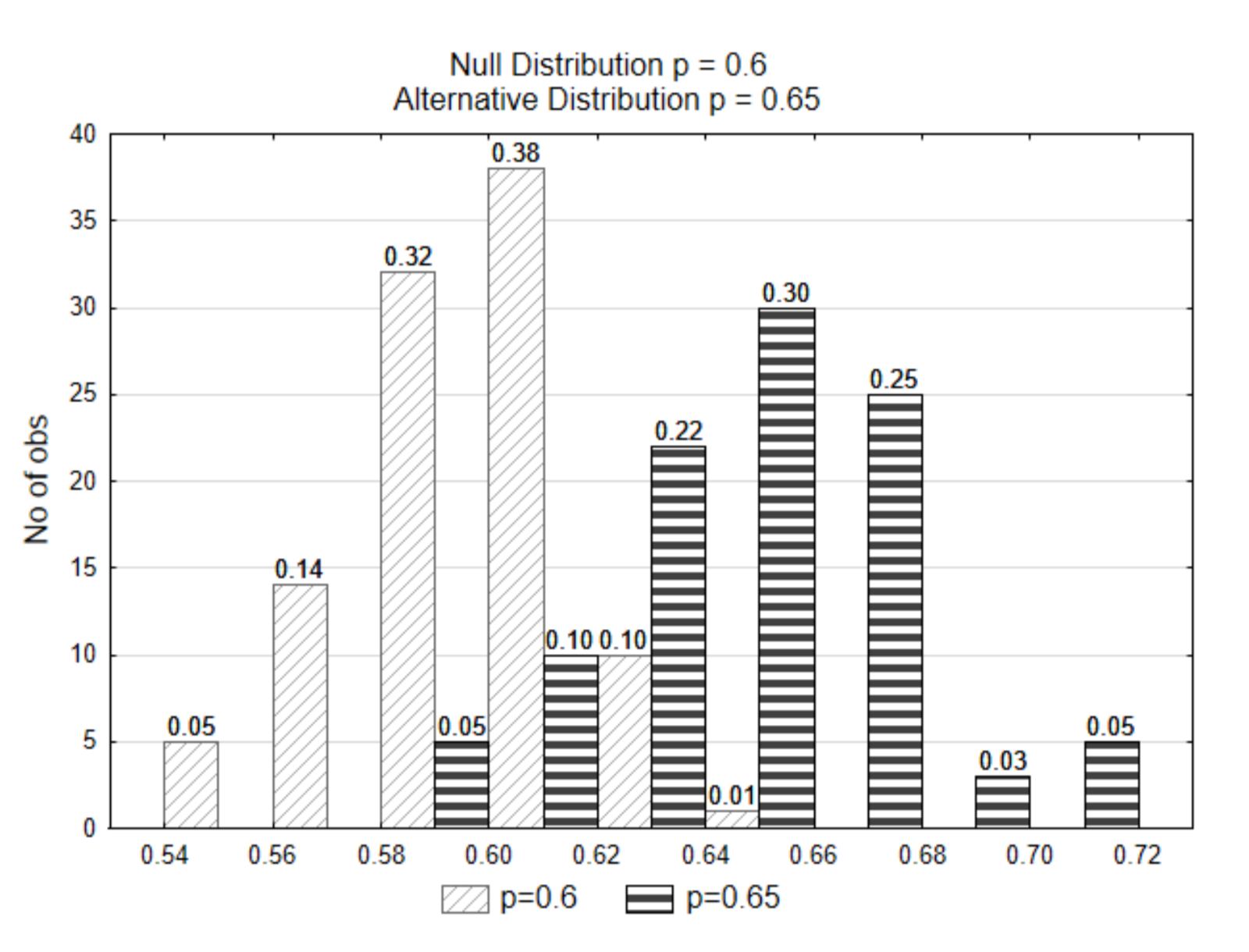
Якщо вибрані дані були\(\hat{p}\) = 0.62, з якого з двох дистрибутивів ви вважаєте, що дані прийшли? Яка гіпотеза підтримується?
Зверніть увагу, що в цьому випадку, оскільки розподіли перекриваються, вибіркова частка 0,62 або більше екстремальних могла б прийти з будь-якого розподілу. Незрозуміло, з якого саме воно прийшло. Через цю відсутність ясності ми могли б зробити помилку. Ми могли б подумати, що він прийшов з нульового розподілу, тоді як він дійсно прийшов з альтернативного розподілу. Або, можливо, ми думали, що це походить від альтернативного дистрибутива, але він дійсно прийшов з нульового розподілу. Як ми вирішуємо???
Перш ніж пояснити, як ми вирішуємо, нам потрібно обговорити помилки, оскільки вони є частиною процесу прийняття рішень.
Існує два типи помилок, які ми можемо зробити в результаті процесу відбору проб. Вони відомі як помилки вибірки. Ці помилки називаються помилками типу I та типу II. Помилка типу I виникає, коли ми думаємо, що дані підтримують альтернативну гіпотезу, але насправді нульова гіпотеза правильна. Помилка типу II виникає, коли ми думаємо, що дані підтримують нульову гіпотезу, але насправді альтернативна гіпотеза є правильною. У всіх випадках тестування гіпотез існує можливість зробити помилку типу I або II типу.
Імовірність допущення помилок типу I або типу II важлива в процесі прийняття рішень. Ми представляємо ймовірність зробити помилку типу I з грецькою літерою alpha, \(\alpha\). Його ще називають рівнем значущості. Імовірність виникнення помилки типу II представлена грецькою літерою Beta,\(\beta\). Імовірність даних, що підтримують альтернативну гіпотезу, коли альтернатива істинна, називається владою. Харчування - це не помилка. Помилки зведені в таблиці нижче.
| Справжня гіпотеза | |||
| \(H_0\)Це правда | \(H_1\)Це правда | ||
| Докази, на яких ґрунтується рішення | Підтримка даних\(H_0\) | Немає помилок | Імовірність помилки типу II:\(\beta\) |
| Підтримка даних\(H_1\) | Імовірність помилки типу I:\(\alpha\) | Ймовірність відсутності помилок: Потужність | |
Процес міркування для вирішення того, яку гіпотезу підтримують дані, передрукований тут.
- Припустимо, що нульова гіпотеза вірна.
- Зберіть дані та розрахуйте статистику.
- Визначте ймовірність вибору даних, які виробляли статистику або могли б створити більш екстремальну статистику, припускаючи, що нульова гіпотеза вірна. Це називається p-значенням.
- Якщо дані ймовірні, вони підтримують нульову гіпотезу. Однак, якщо вони малоймовірні, вони підтримують альтернативну гіпотезу.
Визначення того, чи є дані ймовірними чи ні, ґрунтується на порівнянні між значенням p і α. І альфа, і p-значення є ймовірностями. Вони завжди повинні бути значеннями від 0 до 1 включно. Якщо p- значення менше або дорівнює α, дані підтримують альтернативну гіпотезу . Якщо p-значення більше α, дані підтримують нульову гіпотезу. Коли дані підтримують альтернативну гіпотезу, дані, як кажуть, є значними. Коли дані підтримують нульову гіпотезу, дані не є суттєвими. Перечитайте цей абзац принаймні 3 рази, оскільки він визначає правило прийняття рішень, яке використовується у статистиці, і це критично важливо зрозуміти.
Оскільки деякі значення чітко підтримують нульову гіпотезу, інші чітко підтримують альтернативну гіпотезу, але деякі також не чітко підтримують, тоді має бути прийнято рішення, перш ніж дані коли-небудь збираються (апріорі), щодо ймовірності зробити помилку типу I, яка є прийнятною досліднику. Найпоширенішими значеннями для α є 0,05, 0,01 та 0,10. Немає конкретної причини для цього вибору, але для них є значний історичний пріоритет, і вони будуть регулярно використовуватися в цій книзі. Вибір рівня значущості повинен грунтуватися на декількох факторах.
- Якщо потужність тесту низька через невеликі розміри вибірки або слабку експериментальну конструкцію, слід використовувати більший рівень значущості.
- Майте на увазі кінцеву мету дослідження — «зрозуміти, які гіпотези про Всесвіт є правильними. Зрештою, це так і немає рішень». (Шейнер, Семюель М., і Джессіка Гуревич. Проектування та аналіз екологічних експериментів. Оксфорд [і т.д.: Оксфорд UP, 2001. Друк.) Статистичні тести повинні привести до одного з трьох результатів. Одним з результатів є те, що гіпотеза майже напевно вірна. Другий результат полягає в тому, що гіпотеза майже напевно невірна. Третій результат полягає в тому, що подальші дослідження виправдані. P- значення в межах інтервалу (0,01,0,10) можуть гарантувати продовження досліджень, хоча ці значення є такими ж довільними, як і зазвичай використовувані рівні значущості.
- Якщо ми намагаємося побудувати теорію, ми повинні використовувати більш ліберальні (вищі) значення α, тоді як якщо ми намагаємося підтвердити теорію, ми повинні використовувати більш консервативні (нижчі) значення\(\alpha\).
Демонстрація елементарного тесту гіпотези
Тепер у вас є всі частини для вирішення того, яка гіпотеза підтверджується доказами (даними). Проблема буде переосмислена тут.
\(H_0 : p = 0.6\)
\(H_1 : p > 0.6\)
\(\alpha = 0.01\)
На графіку була проведена вертикальна лінія так, щоб пропорція всього 0,01 була праворуч від прямої в нульовому розподілі. Це називається лінією рішення, оскільки саме лінія визначає, як ми будемо вирішувати, чи підтримує статистика нульова або альтернативна гіпотеза. Число в нижній частині рядка рішення називається критичним значенням.
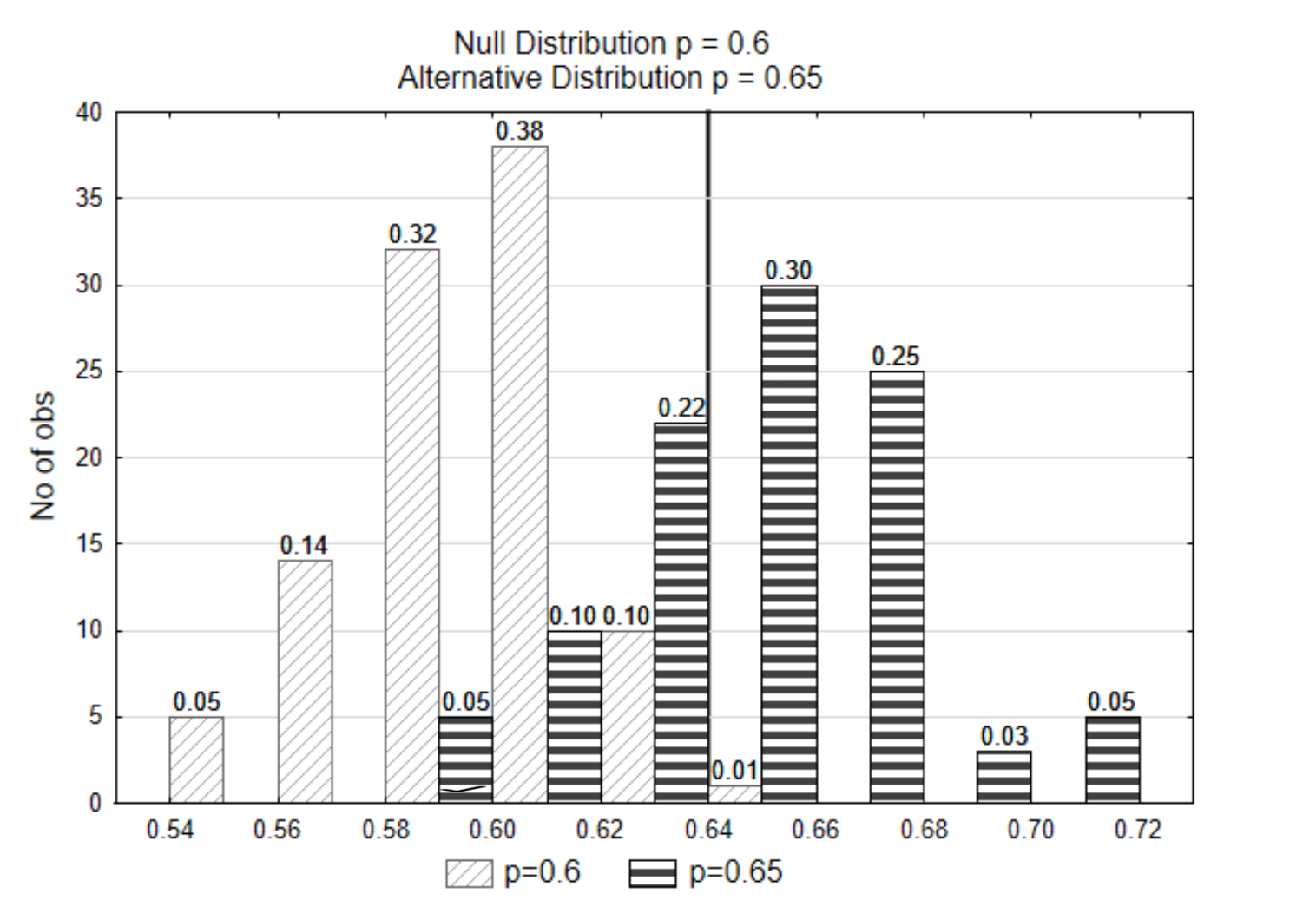
Якщо вибрані дані були\(\hat{p}\) = 0.62, з якого з двох дистрибутивів ви вважаєте, що дані прийшли? Яка гіпотеза підтримується?
Щоб відповісти на ці питання, спочатку знайдіть p-значення. Значення p дорівнює 0,11 (0,10 + 0,01).
Далі порівняємо p-значення з\(\alpha\). Починаючи з 0,11> 0,01, ці докази підтверджують нульову гіпотезу.
Оскільки показ обох розподілів на одному графіку може зробити графік трохи складним для читання, цей графік буде розділений на два графіки. Лінія рішення показана при однаковому критичному значенні на обох графіках (0,64). Рівень значущості α показаний на нульовому розподілі. Він вказує в сторону крайності. β і потужність показані на альтернативному розподілі. Потужність знаходиться на тій же стороні розподілу, що і напрямок крайнього, тоді як β знаходиться на протилежній стороні. Значення p-значення також показано на нульовому розподілі, вказуючи в бік крайності.
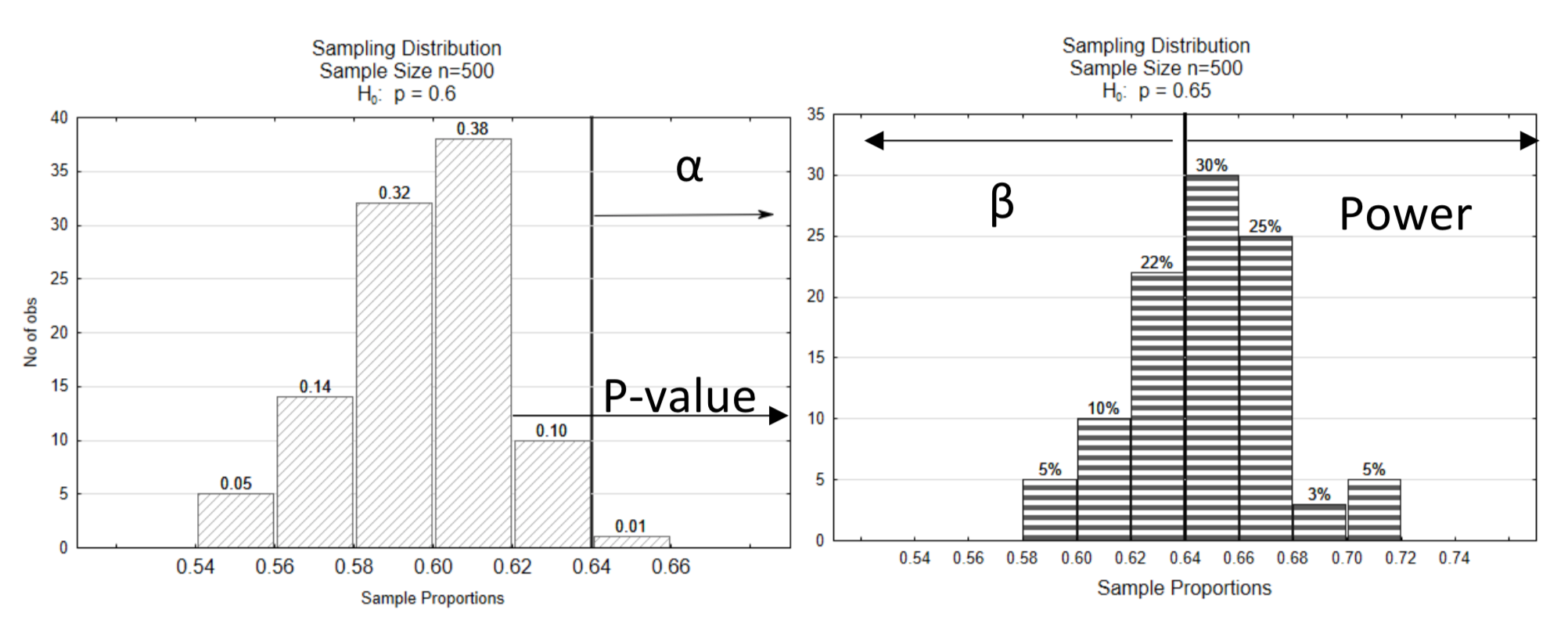
Інший приклад буде продемонстрований далі.
Питання: Яка частка людей, які побували в іншій країні?
Теорія: Частка менше 0,40
Гіпотези:\(H_0: p = 0.40\)
\(H_1: p < 0.40\)
\(\alpha = 0.04\)
Розподіл зліва - це нульовий розподіл, тобто це розподіл, який був отриманий шляхом вибірки з населення, в якому частка людей, які відвідали іншу країну, дійсно становить 0,40. Розподіл праворуч представляє альтернативну гіпотезу.
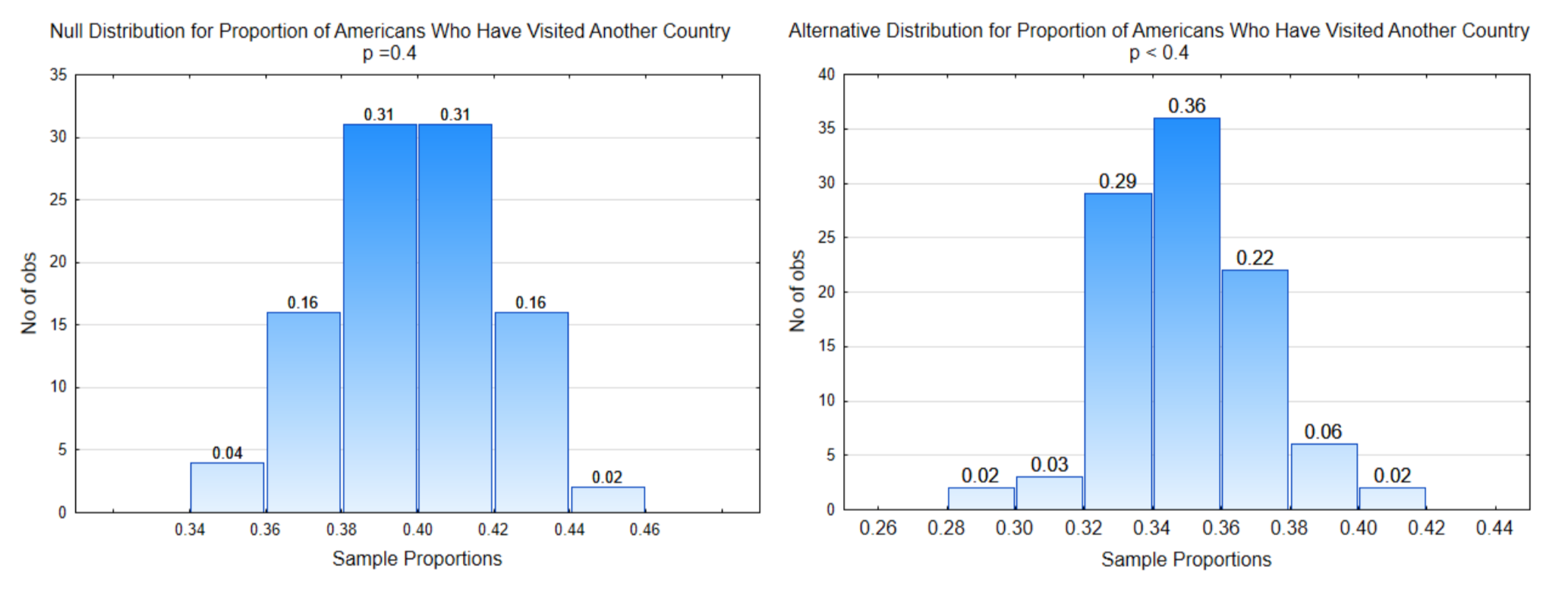
Мета полягає в тому, щоб визначити частину кожного графіка, пов'язану з α, β та потужністю. Після того, як дані будуть надані, ви також зможете показати ту частину графіка, яка вказує на p-значення.
Процес міркування маркування дистрибутивів полягає в наступному.
1. Визначте напрямок крайніх. Це робиться шляхом погляду на знак нерівності в альтернативній гіпотезі. Якщо знак <, то напрямок крайнього - вліво. Якщо знак >, то напрямок крайності - вправо. Якщо знак є\(\ne\), то напрямок крайнього - вліво і вправо, що називається двостороннім. Зверніть увагу, що знак нерівності вказує на напрямок крайніх. Щоб зберегти ці поняття трохи легше, коли ви їх вивчаєте, ми не будемо робити двосторонні альтернативні гіпотези, поки пізніше в тексті.
У цій задачі напрямок крайніх є ліворуч, оскільки менші пропорції вибірки підтримують альтернативну гіпотезу.
2. Намалюйте лінію Рішення. Напрямок крайніх поряд з α використовуються для визначення розміщення лінії рішення. Альфа - це ймовірність виникнення помилки типу I. Помилка типу I може виникнути лише в тому випадку, якщо нульова гіпотеза істинна, тому ми завжди розміщуємо альфа на нульовому розподілі. Починаючи з боку напрямку крайніх, додайте пропорції у верхній частині брусків до тих пір, поки вони не дорівнюють альфа. Намалюйте лінію рішення між смугами, що відокремлюють ті, які можуть призвести до помилки типу I від решти розподілу.
Зверніть увагу на значення осі x у нижній частині лінії рішення. Це значення називається критичним значенням. Визначте критичне значення на альтернативному розподілі та розмістіть там іншу лінію рішення.
У цій задачі напрямок крайніх знаходиться вліво і\(\alpha\) = 4% (0,04), тому лінія рішення розміщується так, щоб частка пропорцій зразка вліво становила 0,04. Критичне значення становить 0,36, тому інша лінія рішення розміщується на рівні 0,36 на альтернативному розподілі.
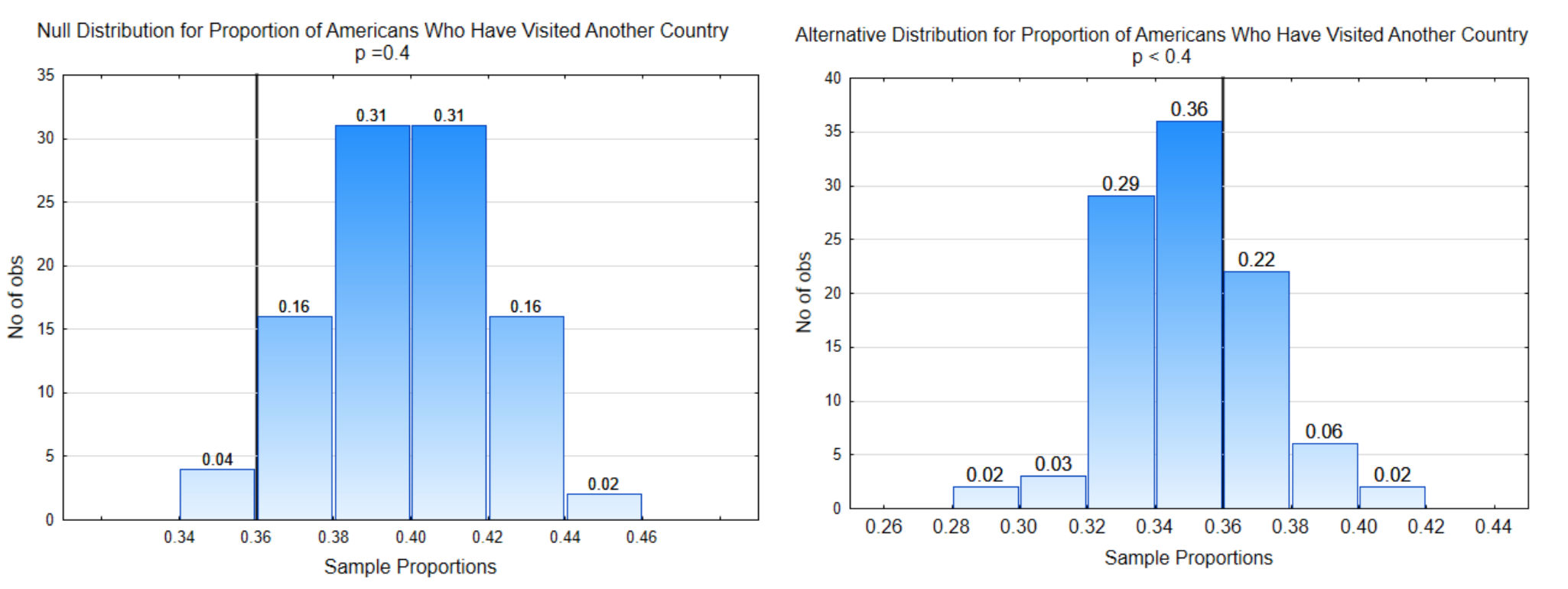
3. Маркування\(\alpha\)\(\beta\) та потужність. \(\alpha\)завжди розміщується на нульовому розподілі на стороні лінії рішення, яка знаходиться в напрямку крайності. \(\beta\)завжди розміщується на альтернативному розподілі на стороні лінії рішення, яка протилежна напрямку крайніх. Потужність завжди розміщується на альтернативному розподілі на стороні лінії рішення, яка знаходиться в напрямку крайніх.
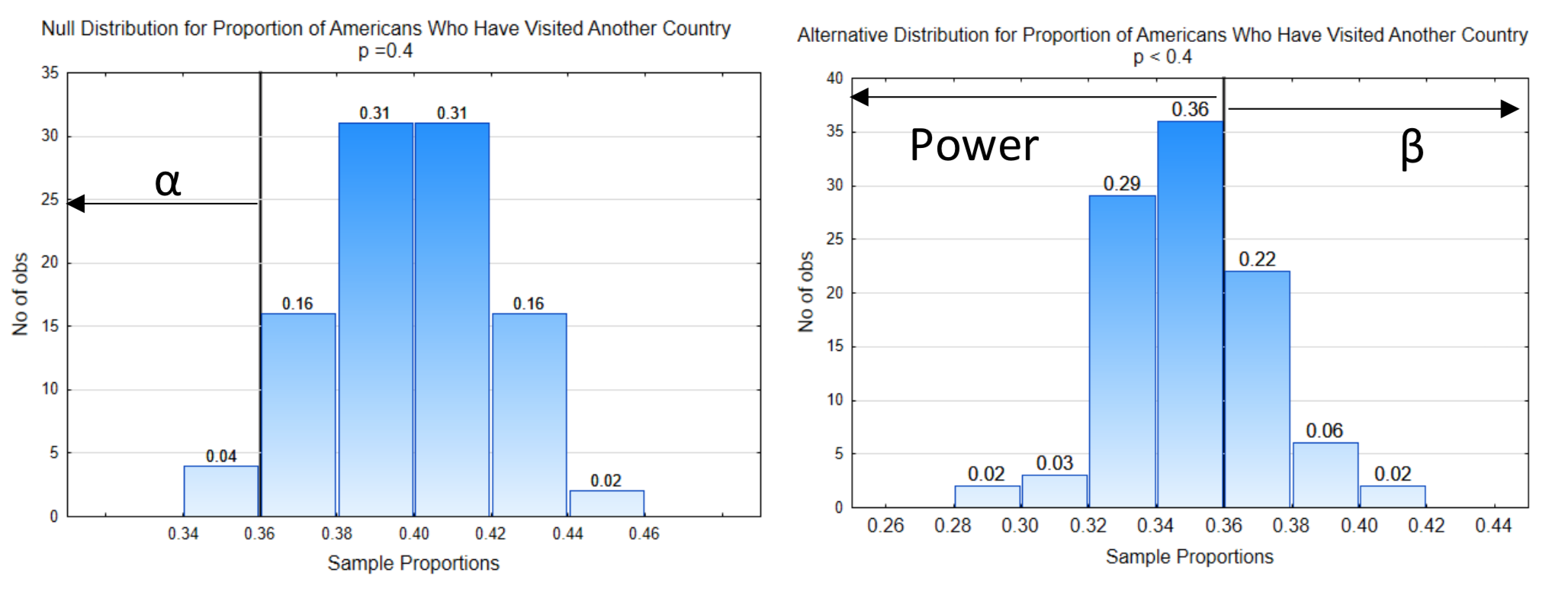
4. Визначте ймовірності для\(\alpha\)\(\beta\), і владу. Це робиться шляхом додавання пропорцій у верхній частині брусків.
У цьому прикладі ймовірність для\(\alpha\) дорівнює 0,04. \(\beta\)Імовірність для 0.30 (0.02 + 0.06 + 0.22). Імовірність потужності дорівнює 0,70 (0,02 + 0,03 + 0,29 + 0,36).
5. Знайдіть p-значення. Дані потрібні для перевірки гіпотези, тому ось дані: У вибірці з 200 людей 72 відвідали іншу країну. Пропорція вибірки становить\(\hat{p} = \dfrac{72}{200} = 0.36\). p-значення, яке є ймовірністю отримання даних, або більш екстремальних значень, припускаючи, що нульова гіпотеза істинна, завжди ставиться на нульовий розподіл і завжди вказує в сторону крайності.
У цьому прикладі p-значення було вказано на нульовому розподілі.
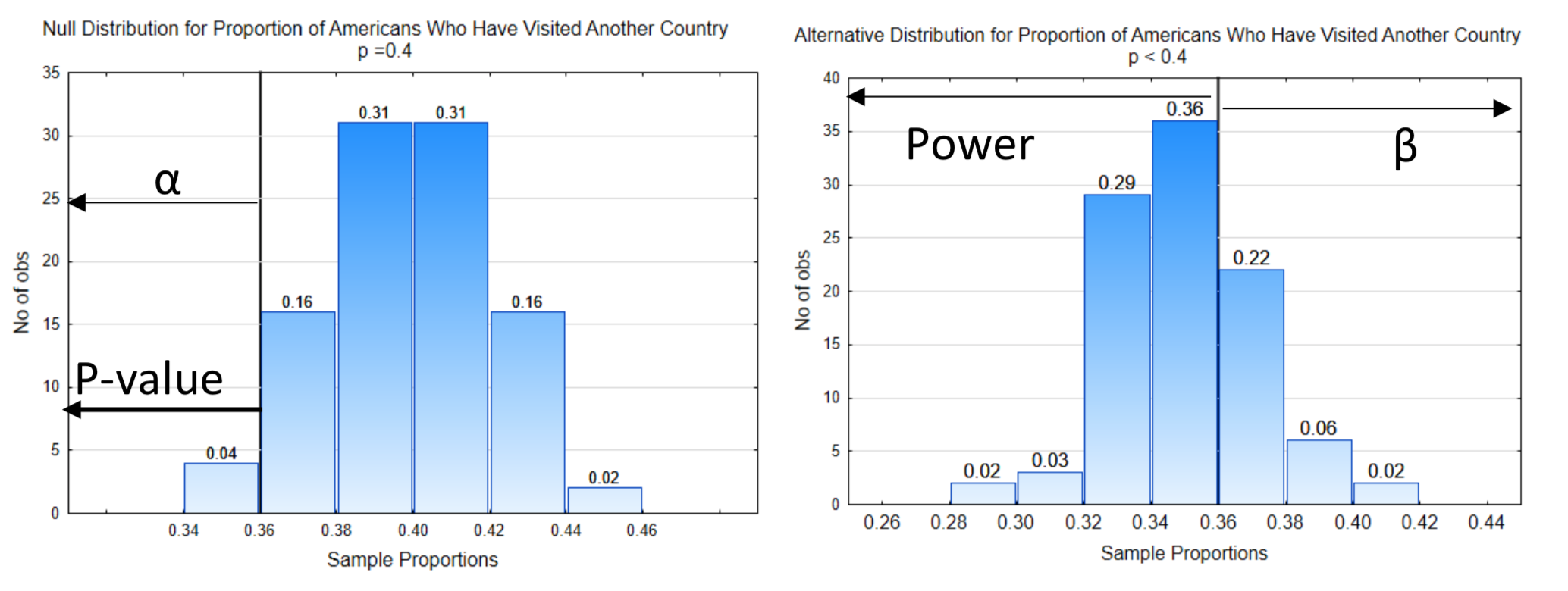
6. Прийміть рішення. Імовірність для p-значення дорівнює 0,04. Щоб визначити, яка гіпотеза підкріплена даними, порівняємо p-значення з альфа. Якщо p-значення менше або дорівнює альфі, докази підтверджують альтернативну гіпотезу. У цьому випадку p-значення 0,04 дорівнює альфа, що також становить 0,04, тому ці докази підтверджують альтернативну гіпотезу, що призводить до висновку, що частка людей, які відвідали іншу країну, становить менше 40%.
7. Помилки і їх наслідок. Хоча ця проблема недостатньо серйозна, щоб мати наслідки, які мають значення, ми, тим не менш, вивчимо наслідки різних помилок, які можуть бути допущені.
Оскільки докази підтвердили альтернативну гіпотезу, ми маємо можливість зробити помилку типу I. Якби ми зробили помилку типу I, це означало б, що ми думаємо, що менше 40% американців відвідали іншу країну, коли насправді 40% зробили це.
На відміну від цього, якби наші дані були 0.38 так що наше p-значення було 0.20, то наші результати підтримали б нульову гіпотезу, і ми могли б зробити помилку типу II. Ця помилка означає, що ми вважаємо, що 40% американців відвідали іншу країну, коли насправді справжня частка була б меншою.
8. Звітність за результатами. Статистичні результати повідомляються у реченні, яке вказує, чи є дані значущими, альтернативною гіпотезою та підтверджуючими доказами, у дужках, які на даний момент включають p-значення та розмір вибірки (n).
Для прикладу, в якому\(\hat{p}\) = 0,36 ми б написали, частка американців, які відвідали інші країни, значно менше 0,40 (p = 0,04, n = 200).
Для прикладу, в якому\(\hat{p}\) = 0,38 ми б написали, частка американців, які відвідали інші країни, не значно менше 0,40 (p= 0,20, n = 200).
У цей момент необхідно коротке пояснення про букву р При вивченні статистики є кілька слів, які починаються з букви р і використовують p як змінну. Список слів включає параметри, чисельність, пропорцію, частку вибірки, ймовірність та p-значення. Параметр слів і популяція ніколи не представляються p. Імовірність представлена позначенням, подібним до позначення функції, яке ви вивчили в алгебрі, f (x), яке читається f з x. Для ймовірності запишемо P (A), який читається ймовірність події А. пропорція і р для p-значення зверніть увагу на розташування р Коли p використовується в гіпотезах\(H_0: p = 0.6\), таких як\(H_1: p > 0.6\),, значить частка населення. Коли в ув'язненні використовується p, наприклад, пропорція значно більше 0,6 (р = 0,01, n = 200), то p в p = 0,01 інтерпретується як p-значення. Якщо задана пропорція вибірки, то вона представлена як\(\hat{p}\) = 0,64.
Ми завершимо цю главу остаточною думкою про те, чому ми формальні в тестуванні гіпотез. За словами Колкухуна (1971), «Більшості людей потрібна вся допомога, яку вони можуть отримати, щоб перешкодити їм зробити дурнів з себе, стверджуючи, що їхня улюблена теорія обґрунтована спостереженнями, які нічого подібного не роблять. І головна функція того розділу статистики, який займається тестами значущості, полягає в тому, щоб не дати людям робити дурнів з себе». (Зелений, 1979).
Глава 1 Домашнє завдання
- Визначте кожне з наведених нижче параметрів або статистики.
А. р є
B
.\(\bar{x}\)\(\hat{p}\) є C
.\(\mu\) є D. - Чи пишуться гіпотези про параметри або статистику? _________________
- Розподіл вибірки - це гістограма якої з наступних?
______оригінальні дані
______можлива статистика, яка може бути отримана при вибірці з популяції - Напишіть гіпотези, використовуючи відповідні позначення для кожної з наступних гіпотез. Використання значущих індексів при порівнянні двох параметрів популяції. Наприклад, порівнюючи чоловіків з жінками, ви можете використовувати сценарії m та w, наприклад\(p_m = p_w\).
4а. Середнє значення більше 20. \(H_0\):\(H_1\):
4б. Пропорція менше 0,75. \(H_0\):\(H_1\):
4c. Середнє значення для американців відрізняється від середнього для канадців. \(H_0\):\(H_1\):
4d. Частка для мексиканців більше, ніж частка для американців. \(H_0\):\(H_1\):
4е. Пропорція відрізняється від 0,45. 4ф. Середнє значення менше 3000. \(H_0\):\(H_1\): - Якщо p-значення менше\(\alpha\),
5a. яка гіпотеза підтримується?
5b. чи є дані значущими?
5c. помилка якого типу може бути зроблена? - Для кожного рядка таблиці задається p-значення і рівень значущості (α). Визначте, яка гіпотеза підтримується, якщо дані значні і який тип помилки може бути допущений. Якщо задане p- значення не є коректним p-значенням (оскільки воно більше 1), поставте x у кожне поле в рядку.
p-значення \(\alpha\) Гіпотеза\(H_0\) чи\(H_1\) Значний чи не суттєвий Помилка
типу I або типу II0.043 0,05 0,32 0,05 0.043 0,01 0,0035 0,01 0.043 0,10 0,15 0,10 5.6\(\times 10^{-6}\) 0,05 7,3256 0,01 - Для кожного набору відомостей, який надається, напишіть заключне речення у формі, яка використовується дослідниками.
7а. \(H_1: p > 0.5, n = 350\), р - значення = 0,022,\(\alpha = 0.05\)
7б. \(H_1: p < 0.25, n = 1400\), р - значення = 0,048,\(\alpha = 0.01\)
7с. \(H_1: \mu > 20, n = 32\), р - значення =\(5.6 \times 10^{-5}\),\(\alpha = 0.05\)
7д. \(H_1: \mu \ne 20, n = 32\), p - значення =\(5.6 \times 10^{-5}\),\(\alpha = 0.05\) - Перевірте гіпотези:
\(H_0: p = 0.5\)
\(H_1: p < 0.5\)
Використовуйте 2% рівень значущості.
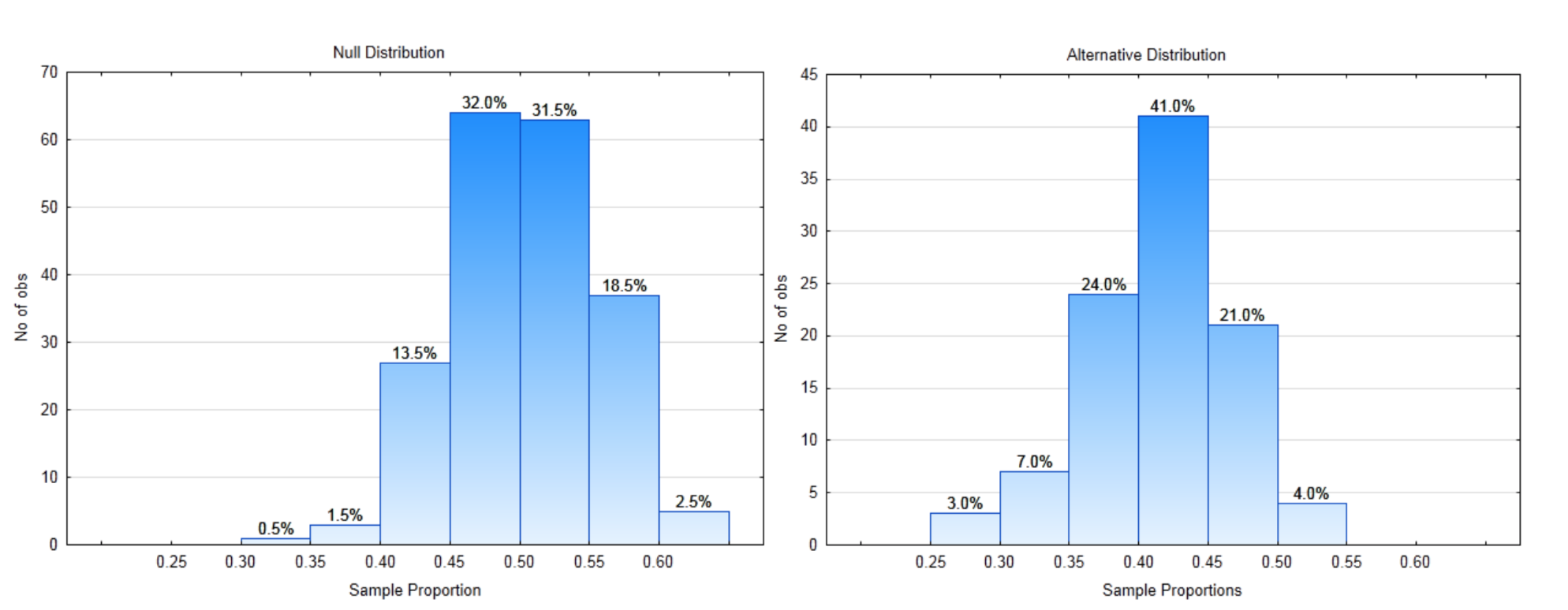
8а. Яке напрямок крайності?
8б. Позначте кожен розподіл рядком правила рішення. Визначити\(\alpha\),\(\beta\), і харчування на відповідному розподілі.
8с. Яке критичне значення?
8д. Що таке цінність\(\alpha\)?
8е. Що таке цінність\(\beta\)?
8ф. Що таке значення Потужність?
Дані: Розмір вибірки 80. Пропорція вибірки становить 0,45.
8 г. Показувати p-значення на відповідному розподілі.
8 годин. Яке значення p-значення?
8i. Яку гіпотезу підтверджують дані?
8 Дж. Чи є дані значущими?
8к. Який тип помилки міг бути допущений?
8 л. Напишіть заключне речення. - Перевірте гіпотези:
\(H_0: \mu = 300\)
\(H_0: \mu > 300\)
Використовуйте 3,5% рівень значущості.
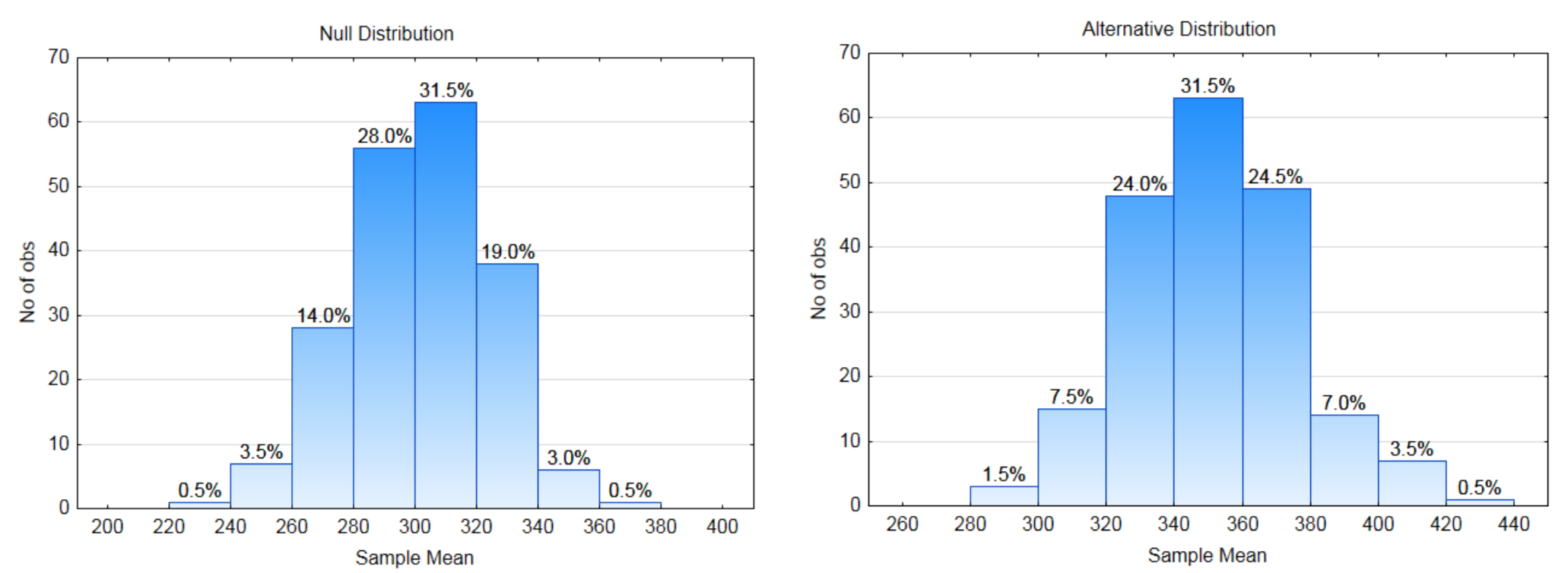
8а. Яке напрямок крайності?
8б. Позначте кожен розподіл рядком правила рішення. Визначити\(\alpha\),\(\beta\), і харчування на відповідному розподілі.
8с. Яке критичне значення?
8д. Що таке цінність\(\alpha\)?
8е. Що таке цінність\(\beta\)?
8ф. Що таке значення Потужність?
Дані: Розмір вибірки становить 10. Середнє значення вибірки - 360.
8 г. Показувати p-значення на відповідному розподілі.
8 годин. Яке значення p-значення?
8i. Яку гіпотезу підтверджують дані?
8 Дж. Чи є дані значущими?
8к. Який тип помилки міг бути допущений?
8 л. Напишіть заключне речення. - Питання: Чи покращується п'ятирічний рівень виживання раку для всіх рас?
.
5 — рік Виживання раку. За даними Американського онкологічного товариства, в 1974-1976 п'ятирічна виживаність для всіх рас становила 50%. Це означає, що 50% людей, у яких діагностували рак, залишилися живими через 5 років. Ці люди все ще можуть проходити лікування, можуть перебувати в стадії ремісії або бути без хвороб. (www.cancer.org/acs/групи/кон... securedpdf.pdf Переглянуто 5-29-13)
Дизайн дослідження: Щоб визначити, чи покращуються показники виживання, дані будуть зібрані від людей, у яких діагностовано рак принаймні за 5 років до початку цього дослідження. Дані, які будуть зібрані, - чи живі люди ще через 5 років після постановки діагнозу. Дані будуть категоричними, тобто люди будуть занесені в одну з двох категорій, виживуть або не вижили. Припустимо, вивчені медичні записи 100 людей з діагнозом рак. Використовуйте рівень значущості 0,02.
10а. Напишіть гіпотези, які були б використані, щоб показати, що частка людей, які переживають рак протягом принаймні п'яти років після встановлення діагнозу, перевищує 0,5. Скористайтеся відповідним параметром.
\(H_0:\)
\(H_1:\)
10б. Яке напрямок крайності?
10с. Позначте нульові та альтернативні розподіли вибірки нижче рядком правила рішення\(\alpha\),\(\beta\),, потужність.
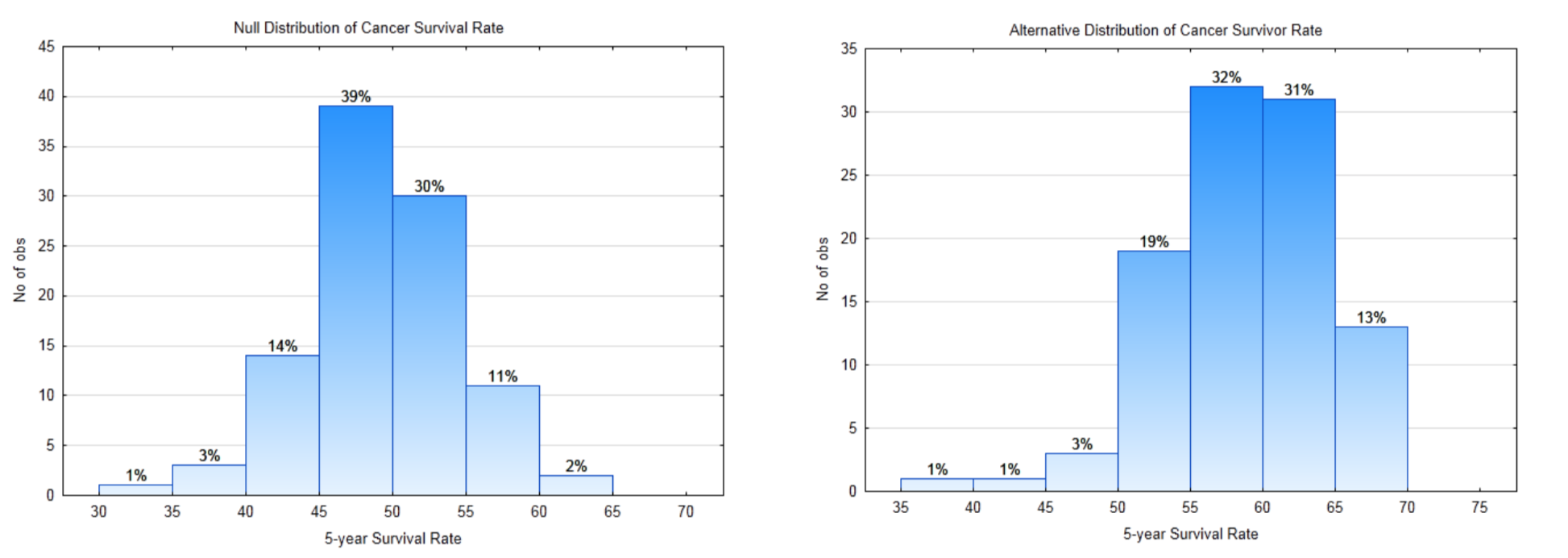
10д. Яке критичне значення?
10е. Що таке цінність\(\alpha\)?
10ф. Що таке цінність\(\beta\)?
10г. Що таке значення Потужність?Дані: 5-річна виживаність становить 65%.
10 год. Що таке p-значення для даних?
10i. Напишіть свій висновок у відповідному форматі.
10 м. Який тип помилки можлива?
10к. Англійською мовою поясніть висновок, який можна зробити з приводу питання. - Чому статистичні міркування важливо для бізнес-студента та професіонала
Розроблено у співпраці з Томом Фелпсом, професором економіки, математики та статистики Ця тема обговорюється в ECON 201, Micro Economics.
Брифінг 1.2
Взагалі кажучи, у міру зростання ціни товару стає менше одиниць придбаного товару. В економічному плані менше «затребуваної кількості». Ставлення процентної зміни необхідної кількості до процентної зміни ціни називається ціновою еластичністю попиту. Формула є\(e_d = \dfrac{\%\Delta Q_d}{\%\Delta P}\). Наприклад, якщо зростання ціни на 1% призвело до зменшення кількості на 1,5%, еластичність ціни становить\(e_d = \dfrac{-1.5\%}{1\%}\) = −1,5. Економісти зазвичай використовують абсолютне значення,\(e_d\) оскільки майже всі\(e_d\) значення є негативними. Еластичність - це одиничне число, яке називається коефіцієнтом пружності.
Їжа - це найважливіший предмет, тому попит завжди буде існувати, однак їсти поза їжею, що дорожче, ніж їсти, не так важливо. Середня цінова еластичність попиту на продукти харчування для дому становить 0,51. Це означає, що зростання цін на 1% призводить до зменшення кількості на 0.51%. Оскільки їсти вдома дешевше, ніж їсти в ресторанах, було б нерозумно припустити, що зі зростанням цін люди їдять рідше. Якщо це так, ми очікуємо, що цінова еластичність попиту на їжу поза приміщеннями буде більшою, ніж для їжі вдома. Перевірте гіпотезу про те, що середня еластичність для їжі далеко від дому вища, ніж для їжі вдома, а це означає, що зміна цін має більший вплив на їжу поза домом. (www.ncbi.nlm.nih.gov/PMC/статті/PMC28046/) (www.ncbi.nlm.nih.gov/pmc/arti... 46/таблиця/tbl1/)
11а. Напишіть гіпотези, які були б використані, щоб показати, що середня еластичність для їжі далеко від дому більше 0,51. Використовуйте рівень значущості 7%.
\(H_0:\)
\(H_1:\)
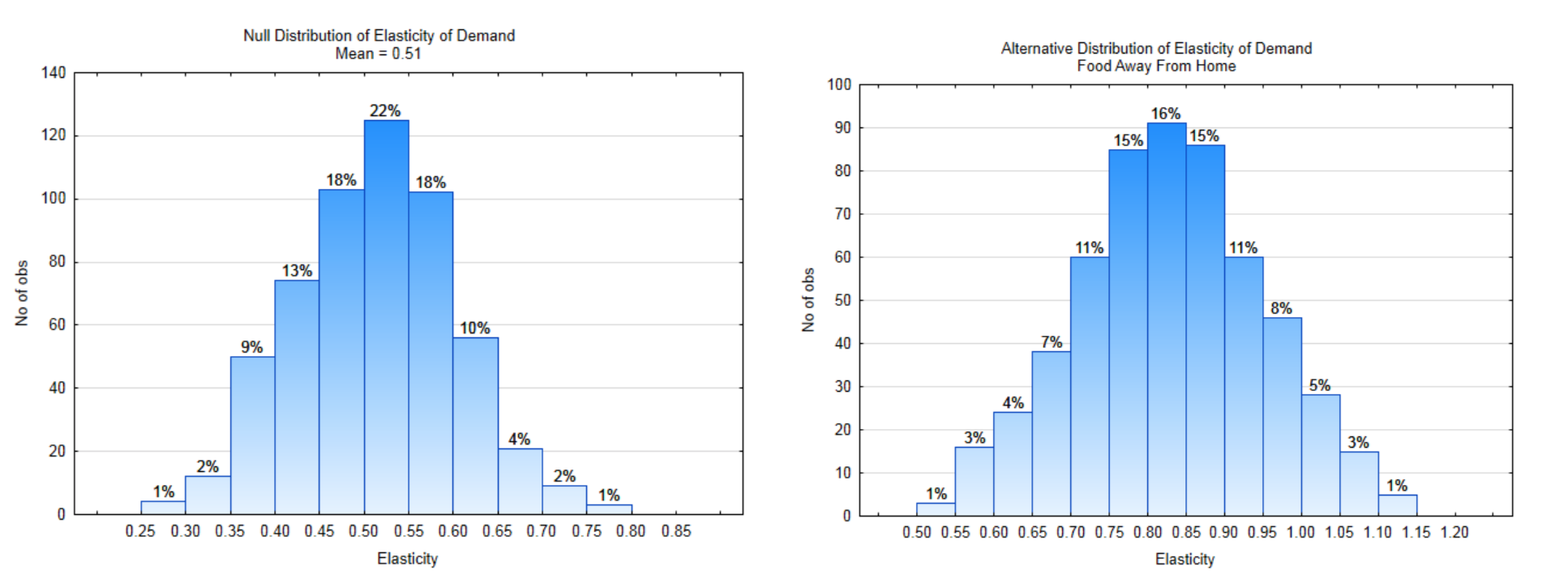
11б. Позначте кожен розподіл рядком правила рішення. Визначити\(\alpha\),\(\beta\), і харчування на відповідному розподілі.
11с. Яке напрямок крайності?
11д. Що таке цінність\(\alpha\)?
11е. Що таке цінність\(\beta\)?
11ф. Що таке значення Потужність?Дані: Вибірка з 13 ресторанів мала середню еластичність 0,80.
11г. Показувати p-значення на відповідному розподілі.
11 год. Яке значення p-значення?
11i. Яку гіпотезу підтверджують дані?
11ж. Чи є дані значущими?
11к. Який тип помилки міг бути допущений?
11л. Напишіть заключне речення.
