2: Отримання корисних доказів
- Page ID
- 97466
Основна роль статистики полягає у використанні доказів стохастичних популяцій для покращення нашого розуміння світу. Вирішення про те, які докази будуть зібрані, є важливою частиною процесу. Дизайн дослідження - це та частина статистичного процесу, в якому планування робиться так, щоб висновки були зроблені з упевненістю і можуть бути підтримані під пильною увагою.
У цьому розділі ми вивчимо три дослідницькі проекти, спостережні дослідження, спостережні експерименти та маніпулятивні експерименти. Тип дослідження, яке проводиться, залежить від мети дослідження. У випадках, коли метою є розуміння популяції або порівняння популяцій, доцільні спостережні дослідження. У випадках, коли ми хочемо визначити, чи існує причинно-наслідковий зв'язок між двома змінними, ми проводимо експеримент. Причинно-наслідковий зв'язок (причинно-наслідкові зв'язки) має на увазі наявність двох змінних. Змінна, яка є причиною, повинна відбутися першою. Перша змінна називається пояснювальною змінною, змінна, на яку впливає, - змінна відповіді.
В експериментах пояснювальна змінна - це лікування або втручання, яке накладається людям або елементам населення. З двох експериментів, спостережних і маніпулятивних, останній краще показує причинно-наслідковий зв'язок. У маніпулятивних експериментах дослідник може випадково призначити лікування або втручання, тоді як для спостережних експериментів лікування або втручання накладається кимось іншим, ніж дослідник.
Перш ніж роз'яснити кожен із цих дослідницьких проектів, кілька прикладів можуть бути корисними.
Приклади спостережних досліджень
- Дослідник може провести опитування американців, щоб порівняти частку демократів, які підтримують зусилля щодо скорочення викидів вуглецю, з часткою республіканців, які хочуть зменшити викиди вуглецю.
- Проби води можуть бути взяті в Puget Sound для визначення рівня забруднення друкованої плати.
- Студентам можна було б дати неоголошений іспит з математичних навичок, які вони вивчили раніше в навчальному році, щоб побачити, скільки вони зберегли.
Приклад експериментів зі спостереженням
- Оскільки деякі штати легалізували рекреаційне використання марихуани, можна визначити, чи дійсно це наркотик шлюзу, побачивши, чи є зміна у вживанні більш твердих наркотиків.
- Коли деякі держави підвищують мінімальну заробітну плату, можна визначити, чи впливає підвищення мінімальної заробітної плати на кількість працюючих в державі людей, порівнюючи їх з державами, які не підвищують мінімальну заробітну плату.
- Коли стихійне лихо вражає район, можна визначити вплив на пожертви таким організаціям, як Червоний Хрест.
Приклад маніпулятивних експериментів
- Тренер випадковим чином призначає деяких бігунів на програму силових тренувань і не дозволяє іншим бігунам піднімати тяжкості, але в іншому всі бігуни мають однакову програму тренувань, тоді тренер може визначити вплив силових тренувань на поліпшення бігу.
- Батони домашнього хліба можна випікати при різних температурах, щоб визначити вплив температури на хліб.
- Компанія може спробувати різні інтернет-оголошення, щоб побачити, чи є вплив на продажі свого продукту.
Випадковість
Кожна дослідницька конструкція включає в себе одне застосування випадковості. У разі спостережних досліджень і спостережних експериментів проводиться випадковий відбір з популяції. Це може бути важко для деяких спостережних експериментів. Наприклад, недостатньо штатів, які легалізували марихуану для випадкового вибору. У маніпулятивних експериментах дослідник випадковим чином призначає учасників до різних груп, наприклад, до груп, які отримують лікування, і тим, хто його не отримує. Методи, які використовуються для випадкового вибору та випадкового присвоєння, розглядаються далі в цьому розділі.
Розмежування дослідницьких конструкцій
Це може бути складним, щоб визначити, який дослідницький дизайн використовується. Наступні питання можуть керувати вашим рішенням.
- Дослідник шукає ефект від лікування чи втручання?
- Якщо відповідь на перше питання ствердна, то чи може дослідник випадковим чином призначити учасників до різних груп?
Наступна блок-схема використовує ці питання для визначення типу дослідницького дизайну.
Типи дослідницької блок-діаграми
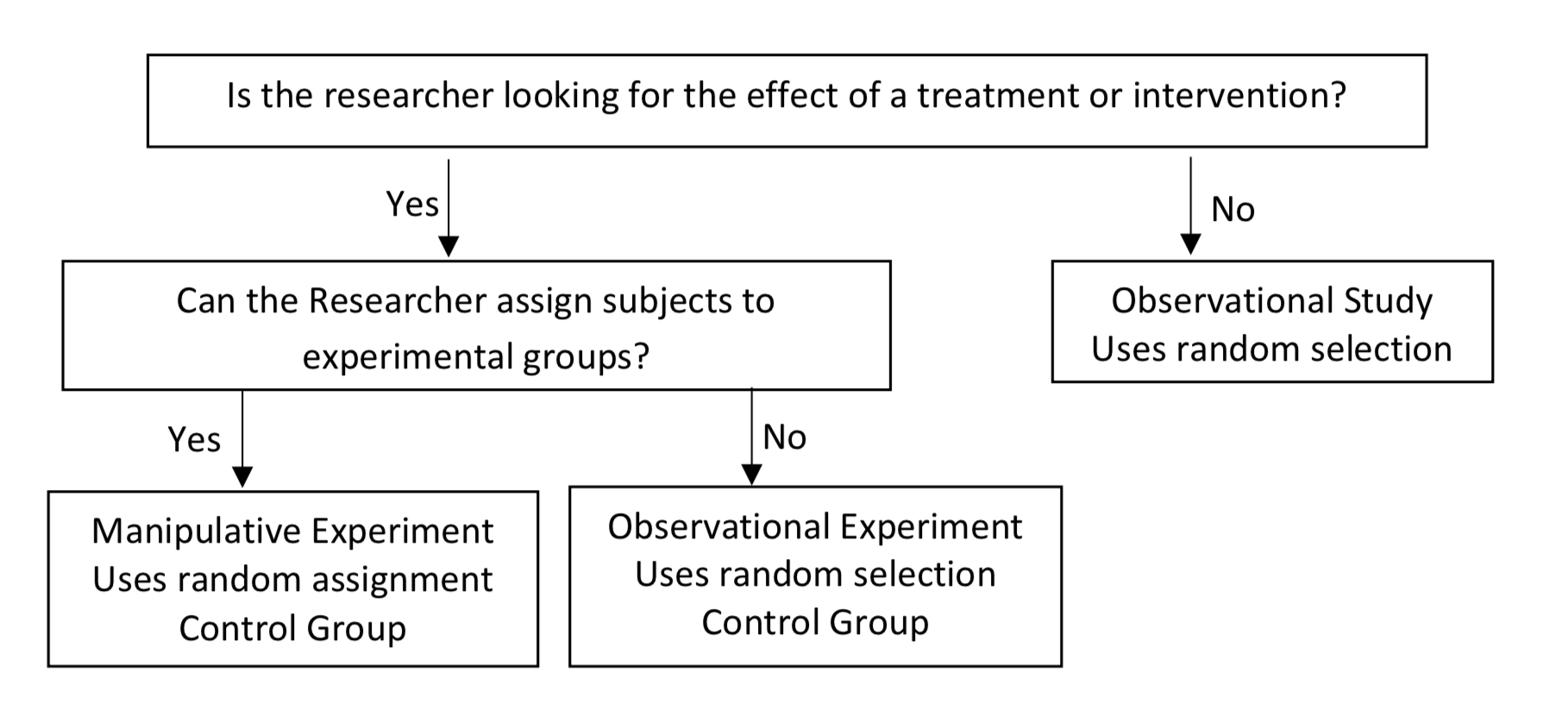
Експерименти
Політики, керівники підприємств, лікарі, освітяни, науковці та тренери, як правило, мають результат, якого вони хотіли б досягти, але вони хочуть прийняти рішення на основі доказів, щоб досягти результату. Тобто вони хочуть знати, яку змінну вони можуть змінити, щоб зміна вплинула на іншу змінну. Наприклад,
Політик може задатися питанням, яку змінну слід змінити, щоб зменшити бідність.
Бізнес-менеджер може задатися питанням, яка рекламна стратегія призведе до найбільшого збільшення продажів.
Лікар може задатися питанням, які ліки вилікує людину.
Вихователь може задатися питанням, яка стратегія викладання призведе до найбільшої кількості навчання для студентів.
Для причинно-наслідкових зв'язків вже було заявлено, що причина повинна протікати наслідком, але є ще один критерій важливості. У причинно-наслідковому зв'язку лікування виробляє певний результат, не забезпечуючи лікування означає, що конкретний результат не виробляється. Таким чином, просто показуючи, що певна відповідь сталася, коли було надано лікування, не доводить, що лікування викликало відповідь. Може бути ще один фактор, який спричинив цю конкретну реакцію. Щоб довести причинно-наслідковий зв'язок, дослідження повинно бути розроблене таким чином, щоб показати, що одна відповідь виникає при лікуванні і не відбувається без лікування і що навряд чи буде інша змінна, яка викликає відповідь. Для цього потрібно мати принаймні дві групи, одну (або більше), яка отримує лікування, і одна, яка не отримує лікування. Група, яка не отримує лікування, називається контрольною групою.
Коли експерименти проводяться на нелюдях, можливо наявність контрольної групи, яка не отримує ніякого лікування. Прикладом можуть бути дослідники сільського господарства, які можуть удобрювати одні культури, але не інші. Однак при проведенні експерименту на людині можуть виникнути ускладнення. У типових експериментах, що передбачають тестування нових ліків на людину з хворобою, недостатньо просто давати деяким людям перевіряється ліки і не давати його іншим. Людина може мати психосоматичні ефекти — фізичні зміни, які є результатом очікувань певного ефекту від медицини, що приписується взаємодіям розум-тіло. Для вирішення цієї проблеми прийнято давати інертні ліки, зване плацебо, деяким учасникам. Важливо, щоб суб'єкти не знали, чи отримують вони справжні ліки чи плацебо. Важливо також, що дослідник, що вивчає предмети, також не знає. Це досягається шляхом проведення подвійного сліпого експерименту. У цьому типі експерименту суб'єкти випадковим чином призначаються або до групи лікування, або до групи плацебо, але не повідомляють, в якій групі вони знаходяться. Лікарю теж не говорять.
Однак проблема спостерігалася з цим типом подвійного сліпого експерименту. Ця проблема називається розривом сліпих і викликана тим, що суб'єкти повинні бути попереджені про можливі побічні ефекти від ліків. Отже, ті, хто відчуває побічні ефекти, можуть здогадатися, що вони приймають фактичне ліки, і ті, які не відчувають їх, роблять висновок, що вони приймають плацебо. У деяких експериментах більше 80% лікарів та випробовуваних правильно визначили, чи був суб'єкт у групі лікування або групі плацебо. Оскільки правильне припущення про групу повинно відбуватися приблизно в 50% часу, цілком ймовірно, що побічні ефекти, або, можливо, інші підказки, призвели до більш високого значення правильної ідентифікації. Щоб допомогти мінімізувати цю проблему, деякі дослідники використовують активне плацебо замість більш типових цукрових таблеток. Активне плацебо виробляє побічні ефекти, подібні до справжніх ліків, але не забезпечує лікування від медичного стану. («Слухання Прозака, але слухання плацебо». Нові наркотики імператора: Вибух антидепресантів міф. Філадельфія: Основні книги, 2010. 7-20. Друк.)
У медичних дослідженнях, окрім групи лікування та групи плацебо, доцільно мати контрольну групу, яка взагалі не отримує лікування. Це часто досягається тому, що деякі люди, які застосовують, щоб бути в експерименті, не приймаються. Оскільки хвороби можуть проходити цикли (хороші дні, погані дні), і люди зазвичай чекають, поки вони відчувають себе дуже погано, щоб отримати лікування, то порівняння результатів лікування з людьми, які не отримують ніякого лікування, може бути корисним, щоб показати, якщо щось інше, ніж нормальний цикл симптомів відбувається в результаті лікування.
Змінні відповіді, пояснювальні змінні, рівні та заплутаність
Відповідь та пояснювальні змінні будуть пояснюватися на прикладі викладачів. Ідеальним результатом для вчителя буде те, щоб весь клас учнів був успішним у класі. Викладач хотів би знати, які стратегії навчання (педагогіка) приведуть до найбільшого успіху для учнів. Зверніть увагу, що в цьому прикладі є дві змінні, стратегія навчання та успіх учнів. Оскільки викладання повинно прийти до оцінки успішності учнів, то стратегія викладання є пояснювальною змінною, а успіх учня - змінна відповіді.
Однак змінна відповіді досить розпливчаста. Що означає успіх учнів? Існує багато аспектів навчання, таких як запам'ятовування фактів, вміння обчислювати, навички в лабораторії, навички письма, здатність мислити критично, здатність мислити творчо тощо Дослідник повинен чітко розуміти змінну відповіді. Наприклад, оскільки ця книга використовується для класу статистики, то одним результатом особливого інтересу є те, чи можуть студенти правильно перевірити гіпотезу. Іншим результатом може бути те, чи можуть студенти створити відповідні графіки для даних.
Існує багато можливостей для пояснювальної змінної стратегій навчання. Ці можливості називаються рівнями. Приклади рівнів включають читання лекцій, активне навчання, навчання відкриттів, програмне забезпечення для комп'ютерного навчання тощо Рівні є конкретними прикладами пояснювальної змінної.
Хоча педагогіка викладання є пояснювальною змінною, яку вчитель може змінити, це не єдина змінна, яка може вплинути на змінну відповіді успіху учня. Інші змінні включають інтерес і мотивацію учня, текст, час навчання, відволікання (відсутність їжі або притулку, розміщення чоловіка, розлучення, хвороба і т.д.). Ці інші змінні, які можуть бути використані як пояснювальні змінні в різних дослідженнях, називаються змішаними змінними. Потенційні змішані змінні повинні бути ідентифіковані на етапі проектування дослідження, щоб ними можна було керувати в експерименті, переконавшись, що вони рівномірно розподілені в різних експериментальних групах.
Щоб отримати практику виявлення різних елементів дослідження, вам будуть надані історії, які пояснюють дослідницький проект. З історії, ваш об'єкт полягає у визначенні ключових елементів, включаючи питання дослідження, змінні, параметр та тип дослідження. Вони будуть організовані в дослідницькій таблиці дизайну. Заповнюючи цю таблицю, подумайте про потенційні змішані змінні самостійно, оскільки вони зазвичай не включаються в історію.
| Дослідження Дизайн Таблиця | |
| Дослідницьке питання: | |
| Тип дослідження | Спостережне дослідження Спостережний експеримент Маніпулятивний експеримент |
| Що таке змінна відповіді? | |
| Що таке параметр, який буде обчислюватися | Середня пропорція |
| Перерахуйте потенційні змішані змінні. | |
| Групування/пояснювальні змінні 1 (якщо є) |
Рівні: |
Деякі з наведених нижче прикладів містять підкреслені слова, інші - ні. Мета підкреслення - допомогти вам визначити ключові слова в історії. Зрештою, вам потрібно визначити ці частини без їх підкреслення.
Приклад 2.1 Чи існує різниця в кількості електронних предметів у будинках людей, які народилися та виросли в США порівняно з людьми, які іммігрували до США і прожили в США щонайменше 5 років?
Щоб відповісти на це питання, статус проживання людей буде класифікований як рідний або 5-річний іммігрант. Будуть взяті випадкові зразки корінних жителів та іммігрантів, які перебували в США не менше 5 років. Всі електронні елементи будуть зараховані індивідуально (наприклад, мобільні телефони, комп'ютери, телевізори, радіоприймачі). Мета полягає в тому, щоб визначити, чи відрізняється середня кількість електронних елементів для двох груп.
| Дослідження Дизайн Таблиця | |
| Питання дослідження: Чи існує різниця в кількості електронних предметів у будинках людей, які народилися та виросли в США порівняно з людьми, які іммігрували до США і прожили в США щонайменше 5 років? | |
| Тип дослідження | Спостережне дослідження Спостережний експеримент Маніпулятивний експеримент |
| Що таке змінна відповіді? | кількість електронних елементів |
| Який параметр буде обчислюватися? | Середня пропорція |
| Перерахуйте потенційні змішані змінні. | Дохід, багатство, вік, розмір сім'ї |
| Групування/пояснювальні змінні (якщо є) Статус резидентства |
Рівні: рідні 5-річний іммігрант |
Брифінг 2.1 Біг босою ногою
У 2011 році Vintage Books опублікував книгу «Народжені бігати: приховане плем'я, суперспортсмени та найбільша раса, яку світ ніколи не бачив» Крістофера Макдугалла. Однією з обговорюваних тем стала концепція бігу голими ногами. Автор стверджував, що біг босою ногою (або з мінімальним захистом між підошвою стопи та землею) призводить до стилю бігу передньої стопи, що призводить до меншої кількості травм, ніж ті, хто бігає з м'яким взуттям та використовує страйк зцілення.
Тренер з бігу середньої школи хотів би знати, якщо нові бігуни, які використовують мінімалістське взуття, що призводять до стилю бігу передньої стопи, матимуть менше травм, ніж нові бігуни, які використовують м'яке взуття, що призводить до загоєння ударів. Тренер використовує монетний фліп, щоб випадково призначити тип взуття, яке повинен носити новий бігун. Тренер запише цей вибір взуття та збереже рекорд травм для кожного спортсмена. В кінцевому підсумку тренер визначить, чи є різниця в частці бігунів з кожної групи, які отримали травму. Тільки нові бігуни будуть включені, тому що було б важко і, можливо, недоречно змінити стиль бігу досвідчених бігунів.
| Дослідження Дизайн Таблиця | |
| Питання дослідження: Чи впливає стиль бігу в травмах? | |
| Тип дослідження | Спостережне дослідження спостережний експеримент Маніпулятивний експеримент |
| Що таке змінна відповіді? | травми |
| Який параметр буде обчислюватися? | Середня пропорція |
| Перерахуйте потенційні змішані змінні. | Попередній досвід бігу, попередні травми, загальна підготовленість |
| Групування/пояснювальні змінні (якщо є) Тип взуття |
Рівні: мінімалістичне взуття Туфлі м'які |
Приклад 2.3 Чи вирішить питання держборгу підвищення податкової ставки для заможних?
Щоразу, коли закон змінюється, країна проводить експеримент. Можна припустити, що законодавці ретельно розмірковують про можливі наслідки будь-яких схвалених ними змін у законі. Зараз країна стикається з великим державним боргом, який стосується деяких законодавців і який іноді привертає інтерес інвесторів. Існує також ідеологічна дискусія, яка триває щодо переваг або наслідків підвищення податків або скорочення витрат. Популярна рекомендація деяких - підвищити податки на заможних.
Брифінг 2.2 Гранична ставка податку
Податкові дужки використовуються для показу суми податку, сплаченого за кожен зароблений долар. Граничні ставки податку на 2013 рік наведені в таблиці на наступній сторінці для осіб, які перебувають у шлюбі, подаючи спільно. (taxfoundation.org/article/us-... використані дужки переглянуті 7/08/13)
Людина, яка заробляє $80,000, буде платити 10% податок на перші $17,488, 15% податок на гроші між $17,488 і $71,030, і 25% від суми понад $71,030.
На графіку нижче показана зміна граничної ставки податку на найбагатших американців та державного боргу. З цього графіка ми бачимо, що державний борг почав сильно зростати наприкінці 1970-х та 1980-х років. Ми також помічаємо, що цьому зростанню передувало велике падіння верхніх граничних податкових ставок під час адміністрації Рейгана.
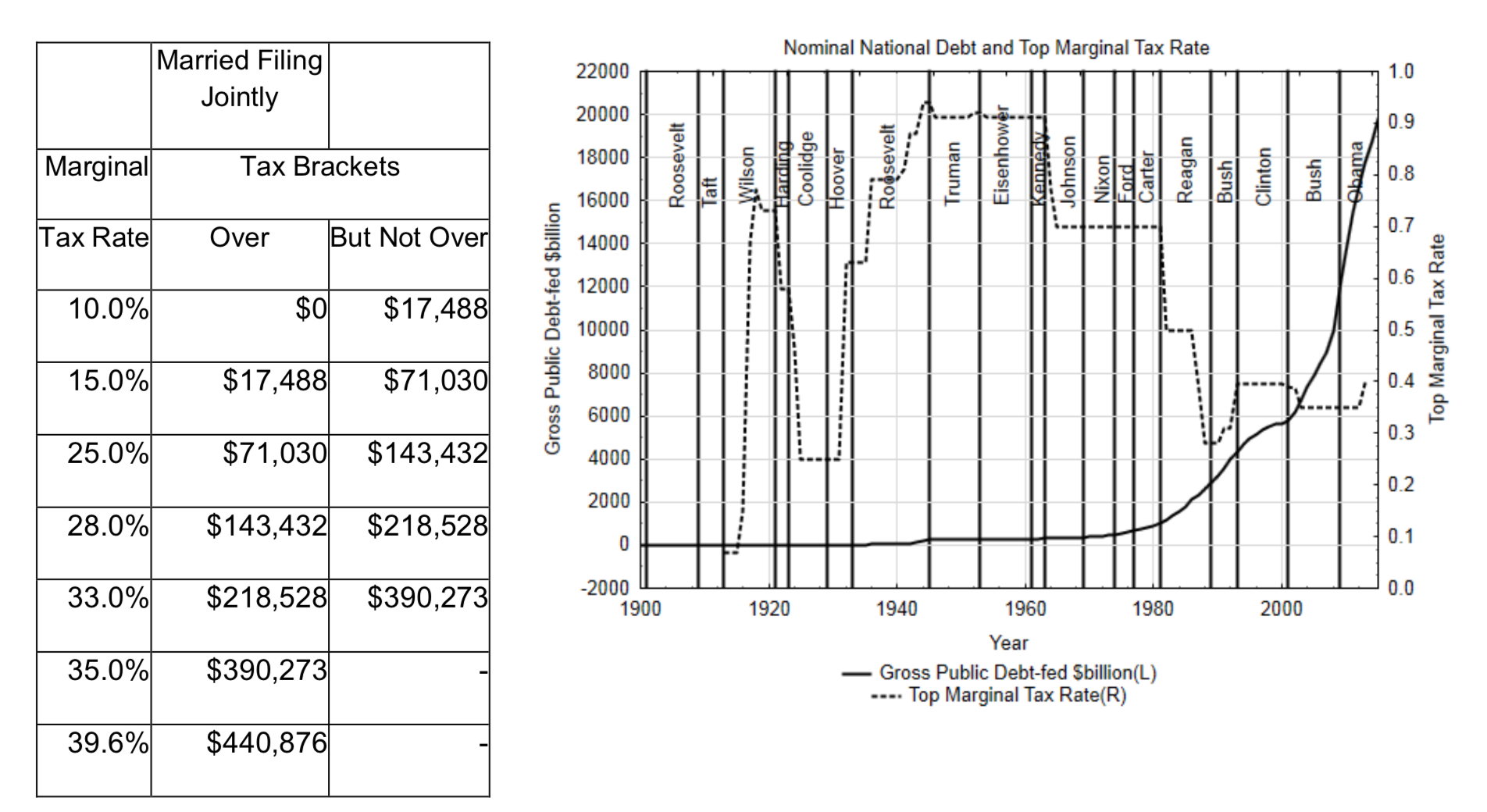
Інформація з цього графіка не може бути використана для перевірки теорії, що зниження податкових ставок призводить до збільшення державного боргу (або навпаки), оскільки теорії не можуть бути доведені доказами, які були використані для створення теорії в першу чергу. Тому, якщо економіст хотів перевірити теорію про вплив граничних ставок податку на державний борг, їм потрібно буде отримати різні дані. Було б нереально очікувати, що будь-яка країна погодиться брати участь в експерименті, в якому науковий економіст змусить їх змінити свої податкові ставки. Однак країни змінюють податкові ставки самостійно, тому дослідник міг спостерігати, що відбувається після кожної такої зміни. Державний борг до зміни ставки і через 5 років після нього можна було визначити. Якщо метою є встановлення причинно-наслідкового зв'язку, також необхідно буде виявити зміни державного боргу для країн, які не змінюють свої податкові ставки. Порівняння змін державного боргу можна було б провести для обох груп. Інші важливі аспекти державного боргу включають обсяг витрат, які робиться, а також обсяг занепокоєння законодавців щодо збереження збалансованого бюджету.
| Дослідження Дизайн Таблиця | |
| Дослідницьке питання: Чи призводить зниження податкових ставок до збільшення держборгу? | |
| Тип дослідження | Спостережне дослідження Спостережний експеримент Маніпулятивний експеримент |
| Що таке змінна відповіді? | Зміни держборгу через 5 років після зміни ставки |
| Який параметр буде обчислюватися? | Середня пропорція |
| Перерахуйте потенційні змішані змінні. | Стан економіки, кількість людей на кожному економічному рівні, пріоритети державного бюджету |
| Групування/пояснювальні змінні (якщо є) Зміна граничної ставки податку |
Рівні: Контроль (не змінювали податкові ставки) Вплив (знижені податкові ставки) |
Відбір проб
Спостережні дослідження та деякі спостережні експерименти вимагають випадкової вибірки з популяції. Наступним кроком процесу проектування дослідження є визначення того, як буде взята вибірка з популяції, щоб вона була репрезентативною для населення. Мета полягає в тому, щоб уникнути упередженості. Упередженість - це систематичне упередження в одному напрямку. Нагадаємо розподіли вибірки, які обговорювалися в главі 1. Половина статистики у розподілі вибірки була меншою за параметр, а половина - більше, таким чином ймовірність отримання статистики вище або нижче параметра була однаковою. Якщо відбір проб зроблений неправильно, легко можна отримати упереджені результати. Це означає, що зразки, швидше за все, будуть меншими за параметр або вони, швидше за все, будуть більшими за параметр. Наприклад, якщо ви хочете визначити, який вид спорту люди вважають найбільш захоплюючим, про футбол або про футбол, і ви тільки зразки людей у місті з командою НФЛ, ви, швидше за все, отримаєте упереджені результати на користь про футбол. З іншого боку, якщо ви проводите своє опитування в такому місті, як Лондон, ви, швидше за все, отримаєте упереджені результати на користь футболу. У будь-якому випадку, ви отримуєте упереджені результати, а це означає, що будь-який висновок, який ви робите, не є дійсним.
Упереджені результати виходять при проведенні добровільного відбору проб і зручності відбору проб. Добровільна вибірка відбувається, коли люди добровільно погоджуються брати участь в опитуванні, наприклад, онлайн-опитуванні або телевізійному опитуванні, де люди можуть надіслати свою відповідь. Зручність вибірки відбувається через отримання відгуків від зручних людей. Цілком можливо, що ці люди поділяють думку і, отже, об'єднуються, що призводить до упереджених результатів.
Найкраща вибірка досягається за допомогою методів вибірки ймовірностей. Чотири методи, про які піде мова:
- Проста випадкова вибірка
- Стратифікований відбір проб
- Систематична вибірка
- Кластерна вибірка
Проста випадкова вибірка
Проста випадкова вибірка відповідає двом бажаним критеріям. По-перше, кожна людина або одиниця в популяції має рівні шанси бути обраними, а по-друге, кожна колекція вибраних одиниць має рівні шанси бути обраними. Розподіли вибірки, які лежать в основі тестування гіпотез, засновані на простому випадковому вибірці з заміною. Це означає, що після вибору одиниця повертається в басейн і може бути обраний знову. Отже, інформацію з одного і того ж блоку можна використовувати не один раз.
Найпростіший приклад простого випадкового зразка - витягування імен з капелюха. Тобто кожен в групі може мати своє ім'я, написане на аркуші паперу, а потім покласти в капелюх або інший контейнер. Хтось змішує папірці, а потім витягує ім'я. Це багато в чому схоже на розіграші, які роблять організації.
Нанесення імен на аркуші паперу швидко стає некерованим з більшим населенням, і тому потрібна інша стратегія. Замість цього кожній людині або одиниці дається число, а потім вибираються цифри. Потім дані збираються від особи або підрозділу з вибраним номером. Три різні методи будуть надані для виконання простого випадкового зразка. Ці методи використовують таблицю випадкових цифр, калькулятор TI83 або TI84 та веб-сайт під назвою Random.Org. Перші два методи відомі як псевдовипадкові означає, що, хоча випадковий процес використовується для генерації чисел, це повторюваний процес. Вони будуть пояснені нижче. Випадкові числа, створені на Random.Org, справді випадкові, оскільки вони засновані на атмосферному шумі. Відвідайте веб-сайт та виберіть генератор цілих чисел, щоб спробувати процес їх вибору.
Таблиця випадкових цифр
Таблиця випадкових цифр складається з цифр 0 — 9, які були обрані випадковим чином, з заміною. Вони згруповані з 5 цифр разом для візуальної зручності. Рядки і стовпці нумеруються.
Щоб скористатися таблицею, визначте чисельність населення, з якої буде проводитися вибірка. Призначте номер кожній людині або одиниці в популяції. Найпростіший спосіб зробити це - призначити 1 першій особі (одиниці), 2 - другій особі (одиниці) тощо Однак це не єдина стратегія. Люди або підрозділи вже можуть мати номер (наприклад, номер студента, виробничий номер), який можна використовувати. Кількість цифр, яке буде вибрано одночасно, відповідає кількості цифр в найбільшому присвоєному номері. Якщо вибір буде здійснюватися з населення розміром 89 одиниць, то оскільки 89 - це 2-значне число, то присвоєні номери будуть 01, 02,... 89 і всі виділення будуть 2 цифри. Якщо чисельність населення дорівнює 745, так як це 3-значне число, то присвоєні номери будуть 001, 002,... 745.
| Ряд | Кол. 1-5 | Кол 6-10 | Кол 11-15 | Кол 16-20 | Черт 21-25 | Кол 26-30 | Кол 31-35 | Кол 36-40 |
|---|---|---|---|---|---|---|---|---|
| 1 | 05902 | 75968 | 00100 | 12330 | 92481 | 64625 | 83012 | 90763 |
| 2 | 53365 | 25560 | 86425 | 45946 | 67093 | 36638 | 71740 | 16878 |
| 3 | 69363 | 06820 | 49676 | 25363 | 96300 | 94376 | 65819 | 19636 |
| 4 | 37520 | 54955 | 31507 | 70745 | 41817 | 86606 | 9766 | 44989 |
| 5 | 10390 | 12738 | 54072 | 03238 | 08294 | 89479 | 03156 | 24217 |
| 6 | 98735 | 90798 | 96609 | 18368 | 74876 | 17403 | 33783 | 85101 |
| 7 | 79609 | 87687 | 77178 | 39784 | 76983 | 05689 | 84023 | 24804 |
| 8 | 00348 | 58777 | 90570 | 09114 | 99677 | 08126 | 76132 | 19334 |
| 9 | 98367 | 93351 | 08246 | 81492 | 57876 | 04366 | 21851 | 28620 |
| 10 | 34588 | 88493 | 61188 | 29234 | 32565 | 82010 | 07425 | 37173 |
| 11 | 74198 | 34943 | 64557 | 2018 | 25540 | 50014 | 29338 | 87231 |
| 12 | 00621 | 86824 | 81204 | 71923 | 03600 | 69080 | 31712 | 3659 |
| 13 | 44684 | 53902 | 86099 | 98640 | 86347 | 88061 | 60420 | 54118 |
| 14 | 43526 | 09310 | 21922 | 40743 | 64742 | 12780 | 88432 | 41496 |
| 15 | 37335 | 98934 | 61403 | 85336 | 76356 | 22349 | 31498 | 34136 |
| 16 | 25488 | 41567 | 32833 | 56973 | 04039 | 5773 | 88677 | 44817 |
| 17 | 45327 | 69347 | 85698 | 03248 | 60079 | 64469 | 71406 | 19478 |
| 18 | 47458 | 08093 | 94256 | 14305 | 42728 | 676159 | 35991 | 13527 |
| 19 | 91622 | 23621 | 91124 | 08233 | 54571 | 73527 | 29012 | 31534 |
| 20 | 77630 | 37356 | 85498 | 21296 | 14880 | 24981 | 70976 | 64922 |
Наприклад, які будуть цифри перших 3 осіб, які будуть обрані з населення з 6890 чоловік? Людям присвоюються такі номери, як 0001, 0002,... 6890. Вибір почнеться в рядку 16, який відтворюється нижче. Підряд буде вибрано чотири цифри. Якщо вони менші або дорівнюють 6890, їх буде вибрано (показано з підкресленням). Якщо вони більші за 6890, вони будуть проігноровані.
| 16 | 25488 | 41567 | 32833 | 56973 | 04039 | 5773 | 88677 | 44817 |
Перші три числа, які обрані, - це 2548, 6732 і 0403.
Калькулятор Texas Instrument TI84 здатний генерувати випадкові цілі числа. Процес, аналогічний вибору рядка в таблиці випадкових цифр, полягає в насінні калькулятора. Калькулятор висівається, а потім вибираються випадкові цілі числа. Наприклад, якщо початкове число дорівнює 38, то натискання клавіш на калькуляторі будуть такими:
38 sto math prb 1 ранд enter. 38 має з'явитися на екрані.
Щоб генерувати випадкове число, натискання клавіш:
математичний привід 5 рандінт, введіть. Функція randint очікує введення трьох чисел, низького, високого та кількості значень, які, на вашу думку, впишуться у вікно екрана. Якщо ми продовжимо приклад 6890 людей, то, оскільки це 4-значне число, ми могли б очікувати, що 3 такі цифри помістяться на екрані, тому ми б ввели: randint (1,6890,3). Якщо нам потрібно більше 3 чисел, то ми можемо просто натиснути Enter знову так часто, як це необхідно.
Числа, які вибрані в цьому прикладі: 2283, 3612, 3884.
Стратифікований відбір проб
Бувають випадки, коли частини населення можуть отримувати інші дані, ніж інші частини. Наприклад, можна очікувати, що концентрація токсичної хімічної речовини в Пьюджет-Саунд буде вищою поблизу промислових районів, ніж у місцях, далеких від цих промислових районів. Оскільки випадкова вибірка може призвести до пропуску ділянок, то можна зробити стратифікований вибірку. При такому підході визначаються області, причому кожна область є прошаруванням. Потім в кожному шарі використовується простий випадковий процес вибірки.
Як окремий приклад, група, яка прагне розширити громадський транспорт у державі, може задатися питанням, скільки підтримки буде для ініціативи. Вони можуть очікувати, що підтримка громадського транспорту буде істотно відрізнятися для людей, які користуються громадським транспортом, ніж для людей, які ніколи не користуються ним. Отже, вони можуть робити просту випадкову вибірку з кожної з цих груп.
Слід зазначити, що розшарування ґрунтується на припущенні, що між шарами будуть відмінності, хоча це може бути не те, що було доведено. Це відрізняється від того, що насправді є гіпотеза про різницю між шарами, і в цьому випадку кожен шар вважається різним населенням, а не різними частинами однієї і тієї ж популяції.
Систематична вибірка
Стратегія вибірки, яка особливо корисна для вибірки даних часових рядів, - це систематична вибірка. Це метод вибірки 1 в k, в якому кожен k\(^{\text{th}}\) unit is selected. Since the value of data in one year may be influenced by the previous year (or more), the data are not independent. For example, this year’s cost of tuition is closely related to last year’s cost. Suppose that a sample is to be taken from time series data that is serially dependent when the data are 1,2 and 3 years separated but not when they are separated by 4 years. In this case, sampling every 4t\(^{\text{th}}\) year would be appropriate. Suppose that data is available from 1961 to the present and a 1 in 4 systematic sampling method is used. What will be the first year in which data are selected? Since every year has to have a chance of being selected, then it will be necessary to randomize the initial value. This will be done by randomly selecting one number between one and k. To find successive numbers, add k to the number selected. For example, if a TI84 calculator is seeded with the number 42, then randint(1961,1964,1) will produce the number 1962. To this will be added 4 repeatedly until a sample of the desired size has been selected. The table below shows the years that will be selected.
| 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | 1970 |
| 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 |
The value of k is dependent upon the size of the population (N) and the size of the sample (n)and is found by dividing the former by the latter: \(K \thickapprox N/n\).
Cluster Sampling
Collecting data can be time consuming and expensive, neither of which is a trivial factor for any organization that needs the data. When data must be collected from different locations and there is not an assumption that the locations will cause the variation in the data, then cluster sampling can be used. For example, a community college may want to sample the student body about charging students a technology fee so that a new student computer lab can be built. Because students take many different classes and these classes are not likely to have a major impact on their preference about the fees, then different classes can be selected and all the students in those classes can be asked their preference on the fees. If a college has 450 classes, they can be numbered from 1 to 450 and a simple random sampling process can be used to select the desired number of classes. If the goal is to select 8 classes and a seed value of 16 is use, then on the TI84, the function Randint(1,450,4) will give the class numbers of 419, 313, 273, 229, 445, 162, 127, 428.
These methods are often confused. The following guidelines may help clarify the differences. Simple Random Sample – Random Sampling is done from the entire population.
Stratified Sampling – The entire population is divided into strata then simple random sampling is done from each strata. The samples from each strata are combined before being analyzed.
Systematic Sampling – One number is randomly selected from the first k numbers. The numbers of the other data are found by adding k to the last number that was selected.
Cluster Sampling – The entire population is divided into groups or clusters, which are given numbers. The groups are randomly selected and every unit within the group becomes part of the sample.
Chapter 2 Homework
Complete the design-layout tables. Use underlined words when available.
- A student would like to know which of two possible routes is faster for the daily trips to school. Route 1 is shorter but has many traffic lights. Route 2 is a little longer but doesn’t have traffic lights. Each morning, a coin flip will be used to determine the route taken to school. The time it takes for the commute will be measured with a stopwatch. After approximately 15 trials on each route, the average time for each will be compared.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Suppose researchers wanted to know if the opinion people had about the future was influenced by the amount of news they consume (watched, listened to, or read). The researchers categorized news consumption into three categories: 5-7 days/week, 1-4 days/week, less than 1 day/week. They then asked the people their opinion of the future (if they expected the future to be better or worse than the present). They will compare the proportion of optimistic people in each group.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Because so many species are becoming extinct, scientists would like to know how to increase biodiversity. There are two approaches to improve biodiversity in the world. The hands-off approach is one in which no one makes any deliberate changes to the environment with the intent of improving biodiversity. The deliberate approach is to deliberately introduce species that will reshape the environment, using surrogate species when necessary (e.g. use elephants instead of woolly mammoths, which are extinct). Examples of the first approach include the DMZ between North and South Korea. An example of the second includes the creation of a Pleistocene park in northeast Siberia by ecologist Sergei Zimov. Whether they occur by accident or design, there is no central planning organization that will randomly determine the approach that will be taken, so researchers can only look at the evidence after ecosystems have been engineered. A comparison will also be made with similar areas (control groups) that do not receive either the hands-off or deliberate approach. The researchers might record data on the increase in the number of species and determine if the average increase in number of species is different for the two approaches and the control groups. (Brand, Stewart. Whole Earth Discipline: An Ecopragmatist Manifesto. New York: Viking, 2009. Print.)
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: 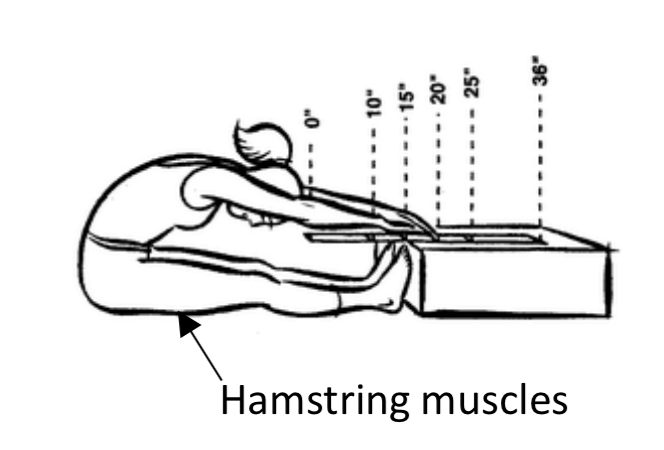 a. It has been hypothesized that a lack of flexibility of the hamstring muscles can contribute to poor posture. To determine if that is the case, a group of adults was randomly selected. The group was divided into two, those with good posture and those with poor posture. The flexibility of their hamstrings was measured using a sit and reach test.(http://silbergen564s15.weebly.com/. Viewed 4/8/2017) The further a person can reach, the greater their hamstring flexibility.
a. It has been hypothesized that a lack of flexibility of the hamstring muscles can contribute to poor posture. To determine if that is the case, a group of adults was randomly selected. The group was divided into two, those with good posture and those with poor posture. The flexibility of their hamstrings was measured using a sit and reach test.(http://silbergen564s15.weebly.com/. Viewed 4/8/2017) The further a person can reach, the greater their hamstring flexibility.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: b. Two types of stretching can be done to improve flexibility, static stretching and dynamic stretching. Static stretching involves stretching a muscle and holding it in a stretched position for about 30 sec. Dynamic stretching involves stretching while moving through a range of motion. To determine which type of stretching resulted in improvement, the group of people with poor hamstring flexibility were randomly assigned to one of three groups. One group did static stretching daily for one month. Once group did dynamic stretching daily for one month. The third group was the control group, which did not do any stretching. Afterwards, the subjects were retested and categorized as improving or not improving since their first test.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Researchers want to know the proportion of acres of forest in the state that show evidence of the brown beetle infestation.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - A teacher wants to know the mean amount of time community college students spend doing homework each night.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - A fisheries biologist want to know the average weight of Coho Salmon returning to spawn.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - In Chapter 2, you were introduced to sampling distributions. Understanding these distributions proves challenging for many but since they form the bases upon which p-values are determined and therefore conclusions are drawn, knowing how the distributions are created and what they mean is helpful for your understanding of statistics. Sampling distributions are really theoretical in nature because they would be extremely difficult to make in reality, but having the experience of partially making one should give you greater insight into what one would really be like. In this problem, you are given a set of data, which is considered the entire population. Each data value has been numbered. You will then practice the various sampling methods multiple times, using different seed values. In each case, you will determine the statistic of the sample, which in this case will be a sample proportion. You will then fill in one box in the distribution that is provided. The first box you put in should be considered the one and only sample that you would have taken. Use a different color for shading the box. The remaining samples you take will represent other possible samples that you would have gotten with a different seed number.
The population consists of all the berths in a harbor. Each dock has room for 20 boats. In this problem, each cluster is a different dock. The two strata are the west side of the harbor and the east side. Yes means there is a boat at the berth, no means that it is vacant.
West Side of Harbor East Side of Harbor Cluster 1 Cluster 2 Cluster 3 Cluster 4 Cluster 5 Cluster 6 Cluster 7 1 Yes 21 No 41 Yes 61 No 81 101 121 2 Yes 22 No 42 No 62 No 82 Yes 102 122 Yes 3 No 23 No 43 No 63 No 83 103 Yes 123 4 Yes 24 No 44 Yes 64 No 84 104 Yes 124 5 No 25 No 45 No 65 No 85 Yes 105 Yes 125 Yes 6 Yes 26 Yes 46 Yes 66 No 86 Yes 106 No 126 No 7 No 27 No 47 No 67 Yes 87 No 107 No 127 Yes 8 Yes 28 No 48 No 68 No 88 No 108 Yes 128 No 9 No 29 No 49 No 69 No 89 Yes 109 No 129 Yes 10 No 30 No 50 No 70 Yes 90 No 110 No 130 No 11 No 31 No 51 Yes 71 No 91 No 111 No 131 No 12 Yes 32 No 52 Yes 72 Yes 92 Yes 112 Yes 132 Yes 13 Yes 33 No 53 Yes 73 Yes 93 No 113 No 133 No 14 Yes 34 No 54 Yes 74 Yes 94 Yes 114 No 134 Yes 15 35 Yes 55 No 75 Yes 95 No 115 No 135 No 16 36 Yes 56 No 76 Yes 96 No 116 No 136 No 17 Yes 37 Yes 57 No 77 No 97 Yes 117 Yes 137 Yes 18 Yes 38 Yes 58 No 78 Yes 98 No 118 Yes 138 No 19 No 39 No 59 Yes 79 No 99 No 119 Yes 139 Yes 20 No 40 No 60 No 80 No 100 No 120 Yes 140 Yes For each sampling method, 20 samples will be taken. Sample with replacement, which means the same number can be selected more than once. Determine the proportion of samples that are Yes. On each line, write the number selected and a Y for yes or N for no (e.g. 8Y)
- In Chapter 2, you were introduced to sampling distributions. Understanding these distributions proves challenging for many but since they form the bases upon which p-values are determined and therefore conclusions are drawn, knowing how the distributions are created and what they mean is helpful for your understanding of statistics. Sampling distributions are really theoretical in nature because they would be extremely difficult to make in reality, but having the experience of partially making one should give you greater insight into what one would really be like. In this problem, you are given a set of data, which is considered the entire population. Each data value has been numbered. You will then practice the various sampling methods multiple times, using different seed values. In each case, you will determine the statistic of the sample, which in this case will be a sample proportion. You will then fill in one box in the distribution that is provided. The first box you put in should be considered the one and only sample that you would have taken. Use a different color for shading the box. The remaining samples you take will represent other possible samples that you would have gotten with a different seed number.
- a. Use a simple random sample. The seed number for what will be considered the official sample is 5.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
The following are alternate sample results you could get if you had used different sampling methods and seed numbers.
b. Use a stratified sample with a seed number of 10 for the West and 11 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______
Sample Proportion ______c. Use systematic sampling with a seed number of 15. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
d. Use a cluster sampling method with a seed number of 20.
Which cluster is selected? ___________ Sample Proportion _________8e. Use a simple random sample with a seed number of 25._______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
f. Use a stratified sample with a seed number of 30 for the West and 31 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______Sample Proportion ______
g. Use systematic sampling with a seed number of 35. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
h. Use a cluster sampling method with a seed number of 40.
Which cluster is selected? ___________ Sample Proportion _________
i. Use a simple random sample with a seed number of 45._______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
j. Use a stratified sample with a seed number of 50 for the West and 51 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______
Sample Proportion ______k. Use a cluster sampling method with a seed number of 55. Which cluster is selected? ___________ Sample Proportion _________
l. Use systematic sampling with a seed number of 60. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
m. Fill in a square in the appropriate column, starting at the bottom row (that does not contain the numbers). The first sample proportion you get (from problem 8a) should be shaded differently than the rest of the sample proportions.0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00
n. Find the parameter by finding the proportion of all the 140 responses that are yes. Show this on the chart in 8m. How do the sample proportions compare to the population proportion? - The first graph shows the change in employment when the Federal minimum wage has been increased. This graph shows a comparison in the number of people employed 6 months after the increase, compared to six months before the increase. The numbers on the x-axis represent millions of people (e.g. 1000 x 1000) with positive numbers reflecting an increase in employment. Notice that most of the time, minimum wage went up, so did employment. However, this graph does not provide solid evidence that raising the minimum wage leads to an increase in employment. This is because there is no comparison. It could be that jobs were increasing or decreasing anyway, because of bigger economic changes, and that the minimum wage had only minor effect.
A better way to determine the effect of raising the minimum wage is to compare states that raise it with states that don’t since states have the ability to raise the minimum wage above the Federal level. The average after – before change in annual unemployment can be compared between these groups of states. For example, if the minimum wage in a state is increased in 2003, then the unemployment rate in 2002 can be subtracted from the unemployment rate in 2003. If the 2003 rate is lower than the 2002 rate, it means the unemployment rate went down and the difference would be a negative number. (Note: while the graph above was about the number of employed people, the graphs that follow are about the number of unemployed people).
a. Complete the Research Design table.Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: Hypotheses and the level of significance are to be established before data is collected. The hypotheses for this question are that the average after-before difference in annual unemployment rates is different in the states that raise their minimum wage compared to states that don’t.
\(H_0: \mu_{\text{Raise}} = \mu_{\text{Not Raise}}\)
\(H_1: \mu_{\text{Raise}} \ne \mu_{\text{Not Raise}}\)
\(\alpha = 0.05\)From the table at http://www.dol.gov/whd/state/stateMinWageHis.htm, minimum wage data is available for consecutive years from 2000 to 2013, with an indication of rate changes beginning in the year 2001. Sampling from this set of data will be done by selecting 3 different years and using all the data from those years.
b. What is the name of the sampling method that is being used? ________________________
Which three years will be selected if your TI84 calculator is seeded with the number 42 and the years 2001 thru 2012 can be selected? These years were chosen because there is minimum wage increase data for these years and unemployment records for the year of, and the year before the unemployment rate increased, are available. Unemployment rates are found at http://www.bls.gov/lau/tables.htm.
c. Which years are selected? _______, ________, _________
The two graphs below are of the actual After-Minus-Before change in unemployment rates for the various states in the years that were randomly selected.
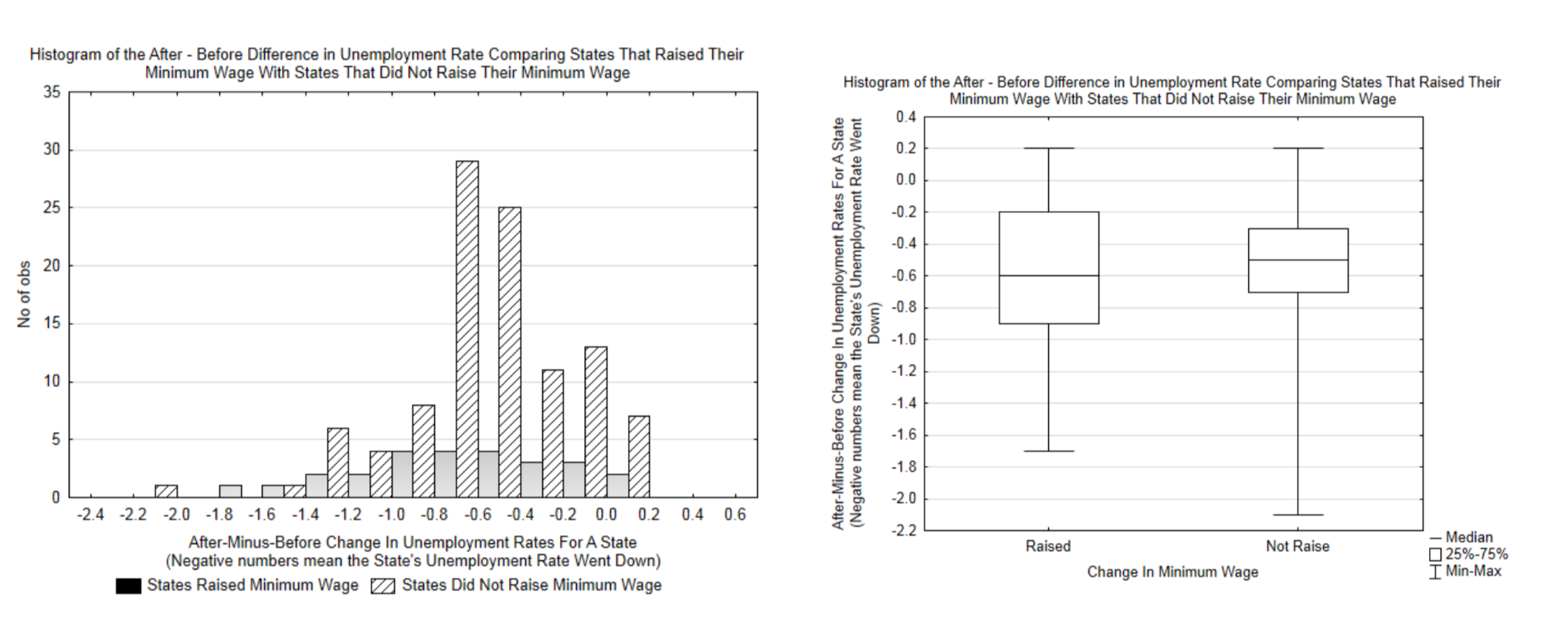
d. Do the graphs appear to support the null hypothesis or the alternate hypothesis better?
e. Both graphs are based on the same data. Which graph do you think shows the data better? Why?
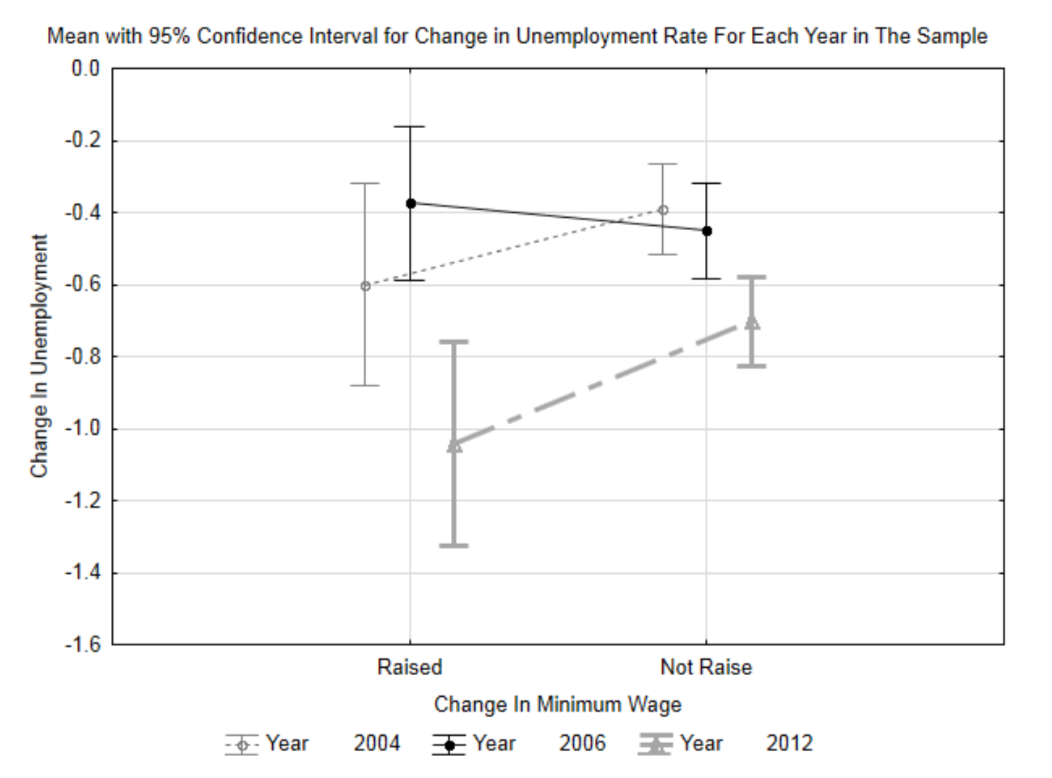 One additional graph is shown to the right. It includes concepts that will be discussed near the end of the book, but because this topic is of interest to the many people working at minimum wage, the graph is being included here. Each line is for a different year. The mean for each year is in the center of the vertical bar. The vertical bars on the left show the change in unemployment for the states that raised their minimum wage and the vertical bars on the right are for the states that did not. The bars represent the confidence interval. Since decreasing unemployment is viewed as desirable, then this graph shows that in two of the years (2004 and 2012), the states that raised their minimum wage reduced their unemployment rate more than the states that didn’t raise their rates. In 2006, the states that didn’t raise their minimum wage reduced their unemployment rate more than the states that did raise their rates.
One additional graph is shown to the right. It includes concepts that will be discussed near the end of the book, but because this topic is of interest to the many people working at minimum wage, the graph is being included here. Each line is for a different year. The mean for each year is in the center of the vertical bar. The vertical bars on the left show the change in unemployment for the states that raised their minimum wage and the vertical bars on the right are for the states that did not. The bars represent the confidence interval. Since decreasing unemployment is viewed as desirable, then this graph shows that in two of the years (2004 and 2012), the states that raised their minimum wage reduced their unemployment rate more than the states that didn’t raise their rates. In 2006, the states that didn’t raise their minimum wage reduced their unemployment rate more than the states that did raise their rates.
f. The table below shows the average change in unemployment rates for all the data combined. Which hypothesis do these statistics support?States Raised Minimum Wage States Did Not Raise Minimum Wage Mean -0.615 -0.519 n 26 105 g. The p-value for a comparison of the two means is 0.286. Write a concluding sentence in the style used in scholarly journals (like you were taught in Chapter 1).
h. Suppose you were in a class in which this topic was being discussed. What would you say to a classmate who argued that the minimum wage should not be raised because it will lead to more unemployment?
What would you say to the classmate who argued that the minimum wage should be raised because it means the poorer people will have more money to spend which means businesses will do better and have to hire more people thereby causing unemployment to drop even more?
- Why Statistical Reasoning Is Important for a Nursing Student and Professional Developed in collaboration with Becky Piper, Pierce College Puyallup Nursing Program Director This topic is discussed in NURS 112.
This problem is based on An Analysis of Falls in the Hospital: Can We Do Without Bedrails?by H.C. Hanger, M.C. Ball and L.A. Wood. the American Geriatrics Society, 47:529-531.
There was a time when women who helped the sick and injured were poorly regarded. However, in 1844, Florence Nightingale, daughter of a British banker, started visiting hospitals and learning about the care of patients. She eventually provided leadership to the British field hospitals during the Crimean War of 1853-56.(http://en.Wikipedia.org/wiki/Crimean_War) While her efforts helped improve the quality of the hospitals, it was after the war that she reflected about results she considered disappointing. She sought the assistance of William Farr who had recently invented the field of medical statistics. To help Florence understand the reasons for all the deaths in the hospital, he suggest that “We do not want impressions, we want facts.” One of her theories had been that many of the deaths were the result of inadequate food and supplies. The statistics lead to a rejection of this theory and instead pointed to lack of sanitation as a cause.(https://www.sciencenews.org/article/...e-statistician) Nightingale was also known for her use of graphs as a way of showing her analysis. Because of Florence Nightingale, the profession of Nursing is inextricably linked with statistics. In the modern context, it is called “evidence-based practices”.
Because hospital patients, particularly the elderly, have physical and possible cognitive problems that required placement in a hospital or nursing home, there is a need for nurses to keep the patients safe. One problem for these patients is falls, including falling out of bed. A standard practice for facilities has been to use bedrails so that a patient doesn’t accidently roll out of bed.
The researchers who wrote the article could find no evidence that bedrails prevented falls, so they conducted their own experiment. They instituted a policy at their hospital (in Christchurch, NZ) to discontinue the use of bedrails unless there was a justifiable reason for their use that was documented and approved. Their experiment was to compare the average number of falls per 10,000 bed days after the implementation of the policy to before its implementation. If the bedrails helped reduce falls, the number of falls should increase after they are removed.
\(H_0: \mu_{\text{after}} = \mu_{\text{before}}\)
\(H_1: \mu_{\text{after}} > \mu_{\text{before}}\)
\(\alpha = 0.05\)
a. Complete the experiment design tableResearch Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: b. Before implementing the policy, the average number of falls per 10,000 bed days was 164.8 (S.D. = 20.6). After the new policy was implemented, the average number of falls per 10,000 bed days was 191.7 (S.D. = 40.7). The p-value was 0.18. Write a complete concluding sentence.
c. An additional part of the experiment was to compare the severity of the falls. Falls were classified as serious injury, minor injury or no injury. The table below shows the distribution of the injuries.Pre-policy Post-policy Serious injury 33 18 Minor injury 43 60 No injury 110 154 There is a significant difference in the injuries (p = 0.008). Explain what the difference is and give a possible reason for the difference.
d. If you were a nurse, would you suggest that bedrails be required or be removed? Why?
