Skip to main content
LibreTexts - Ukrayinska

9: Заняття в класі

  1. Last updated
  2. Save as PDF
  • Page ID
    97390

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Глава 1 Дані та статистика

    1. Питання опитування запитало, чи чекали ви з нетерпінням часу, коли більшість автомобілів на дорозі були самохідними (автономними) автомобілями, і вибір відповідей був так чи ні.

      а Чи є дані відповідей на це питання категоричними або кількісними?

      б) Чи є відповідною статистикою\(\hat{p}\) чи\(\bar{x}\)?

      в Таблиці нижче наведені відповіді на 20 питань. Обчисліть значення відповідної статистики, яка використовується для відповіді «так».
      ні так так так ні ні так ні ні так
      так ні так ні так ні так так так ні
    2. У їдальні школи співробітник підраховував кількість людей, що сидять за кожним столом.

      а Чи є дані відповідей на це питання категоричними або кількісними?

      б) Чи є відповідною статистикою\(\hat{p}\) чи\(\bar{x}\)?

      в Таблиці нижче наведено число на 10 різних таблицях. Обчисліть значення відповідної статистики.

      5 6 8 7 4
      1 7 8 3 1

    Глава 1 Написання гіпотез

    Ім'я___________________________ Зусилля _____/4 Відвідуваність ____/1 Всього ____/5

    1. Знак рівності завжди повинен йти в нульовій гіпотезі (\(H_0\))
    2. Знак рівності ніколи не може з'явитися в альтернативній гіпотезі (\(H_1\))
    3. Альтернативна гіпотеза використовує одну з наступних дій: <, >,\(\ne\)
    4. Обидві гіпотези повинні бути приблизно однаковим параметром (середнє (μ) або пропорція (p)). Якщо гіпотеза стосується пропорції, то використовуйте\(H_0: p = a\) число між 0 і 1. Якщо гіпотеза про середнє значення, використовуйте\(H_0: \mu = a\) число.
    5. Число в нульовій і альтернативній гіпотезі має бути однаковим.

    Приклад: Яка частка студентів сьогодні снідала?
    \(H_0: p = 0.60\)
    \(H_1: p < 0.60\)

    Приклад: Яка середня кількість калорій, споживаних на сніданок сьогодні студентами?
    \(H_0: \mu = 200\)
    \(H_1: \mu > 200\)

    Напишіть свої гіпотези для кожного питання. Використовуйте кожне з трьох нерівностей хоча б один раз.

    1. Яка середня частота серцевих скорочень студентів коледжу?

      \(H_0: \)
      \(H_1: \)
    2. Враховуючи вибір між людством, що створює фантастичне майбутнє за допомогою технологій або страждає крахом суспільства через виснаження ресурсів та інші екологічні проблеми, яка частка студентів коледжу, на вашу думку, вважає, що майбутнє буде фантастичним?

      \(H_0: \)
      \(H_1: \)
    3. Який середній час, у хвилинах, потрібно учням, щоб потрапити в школу вранці?

      \(H_0: \)
      \(H_1: \)
    4. Яка частка студентів їдять сире тісто для печива?

      \(H_0: \)
      \(H_1: \)

    Розділ 1 Розподіли вибірки

    1. У розподілі праворуч: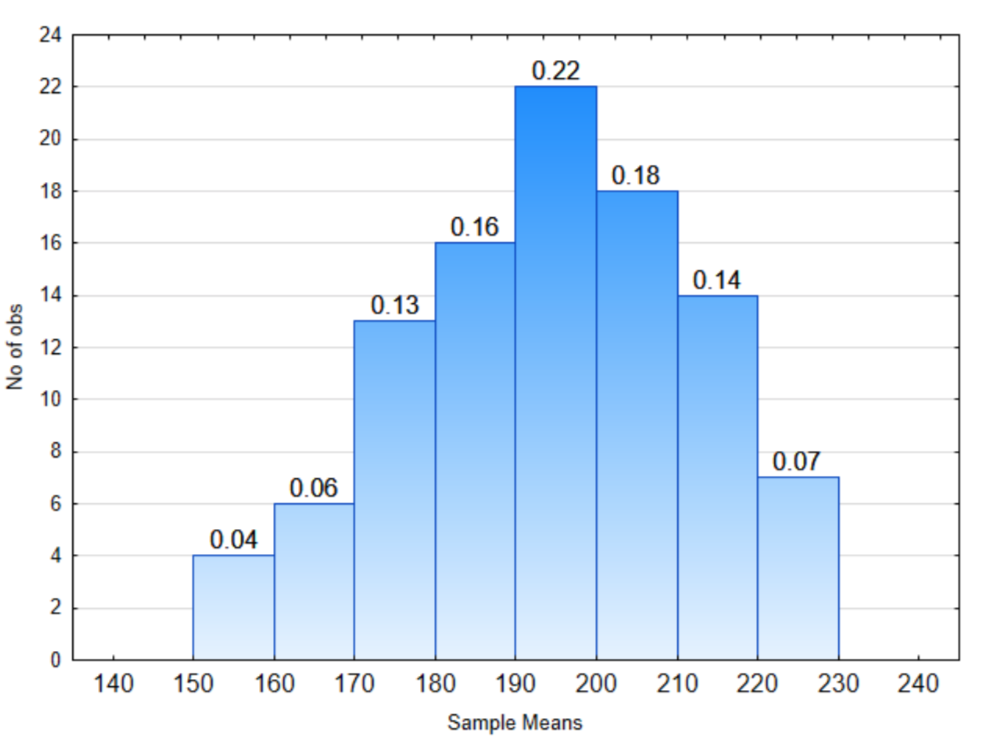2019-05-21 3.29.05.png

    Яка частка вибіркових засобів буде між 150 і 170?

    Яка частка вибіркових засобів буде між 200 і 230?

    Яка частка вибіркових засобів буде між 150 і 230?

    2. У розподілі праворуч: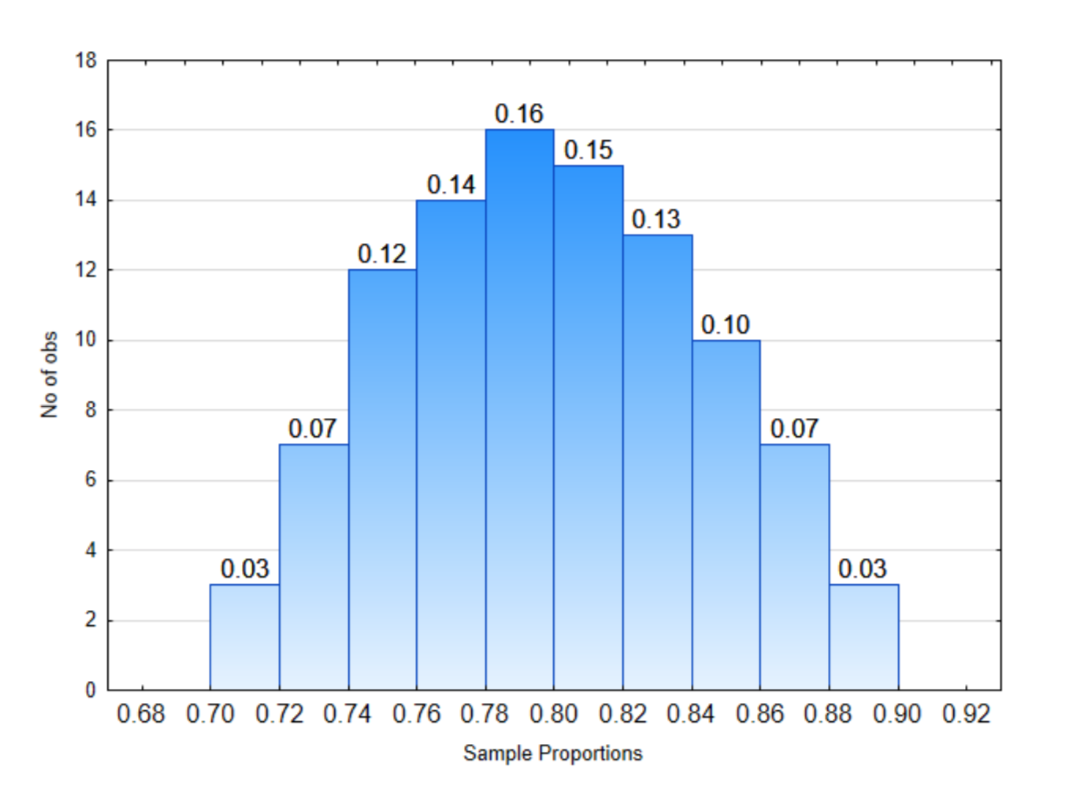2019-05-21 3.29.40 пнг

    Яка частка пропорцій зразка буде між 0,70 і 0,74?

    Яка частка пропорцій зразка буде між 0,84 і 0,90?

    Яка частка пропорцій зразка буде менше 0,70?

    Глава 2 p-значення і рівні значущості

    1. Для кожного рядка таблиці задається p-значення і рівень значущості (\(\alpha\)). Визначте, яка гіпотеза підтримується, якщо дані значні і який тип помилки може бути допущений. Якщо задане p-значення не є коректним p-значенням, поставте x у кожне поле в рядку.
      p - значення \(\alpha\) Гіпотеза\(H_0\) чи\(H_1\) Значний чи не суттєвий Помилка
      типу I або типу II
      0,48 0,05
      0,023 0,10
      6.7Е-6 0,01

      Визначте кожен як істинний або хибний, якщо дані не є значними
      _____ Нульова гіпотеза безумовно вірна
      _____ Альтернативна гіпотеза безумовно вірна
      _____ Альтернативна гіпотеза відхилена
      _____ Нульова гіпотеза не була відхилено
      _____p-значення більше\(\alpha\)

    2. Для кожного рядка таблиці задається p-значення і рівень значущості (\(\alpha\)). Визначте, яка гіпотеза підтримується, якщо дані значні і який тип помилки може бути допущений. Якщо задане p-значення не є коректним p-значенням, поставте x у кожне поле в рядку.
      p - значення \(\alpha\) Гіпотеза\(H_0\) чи\(H_1\) Значний чи не суттєвий Помилка
      типу I або типу II
      0,048 0,05
      0,0023 0,10
      6.70 0,01


      Визначте кожен як істинний або хибний, якщо дані не є значними
      _____ Нульова гіпотеза, безумовно, вірна
      _____ Альтернативна гіпотеза, безумовно, вірна
      _____ Альтернативна гіпотеза відхилена
      _____ Нульова гіпотеза не була відхилена
      _____p-значення більше\(\alpha\)

    Елементарний тест гіпотези, приклад 1 Миш'як

    Брифінг: Миш'як є природним елементом, а також людським виробленим елементом (наприклад, фрекінг, спалювання вугілля), які можна знайти в грунтових водах. Він викликає різноманітні проблеми зі здоров'ям і може призвести до летального результату. Ліміт EPA становить 10 ppb, тобто 10 ppb або вище небезпечно. Проблема: Fracking було розпочато у вашій громаді. Через рік хвороба в громаді змушує посадових осіб департаменту охорони здоров'я перевірити вашу воду, щоб визначити, чи забруднена вона миш'яком. Чиновник візьме 5 проб води протягом наступних 2 місяців і вирішить, чи є у вас безпечна вода або небезпечна вода на основі середнього показника цих зразків. Гіпотези, які потрібно перевірити, такі:\(H_0: \mu = 10\) (Небезпечно)\(H_1: \mu < 10\) (Безпечно). Рівень значущості:\(\alpha = 0.12\).

    Припустімо, що це два можливі дистрибутиви, які існують.

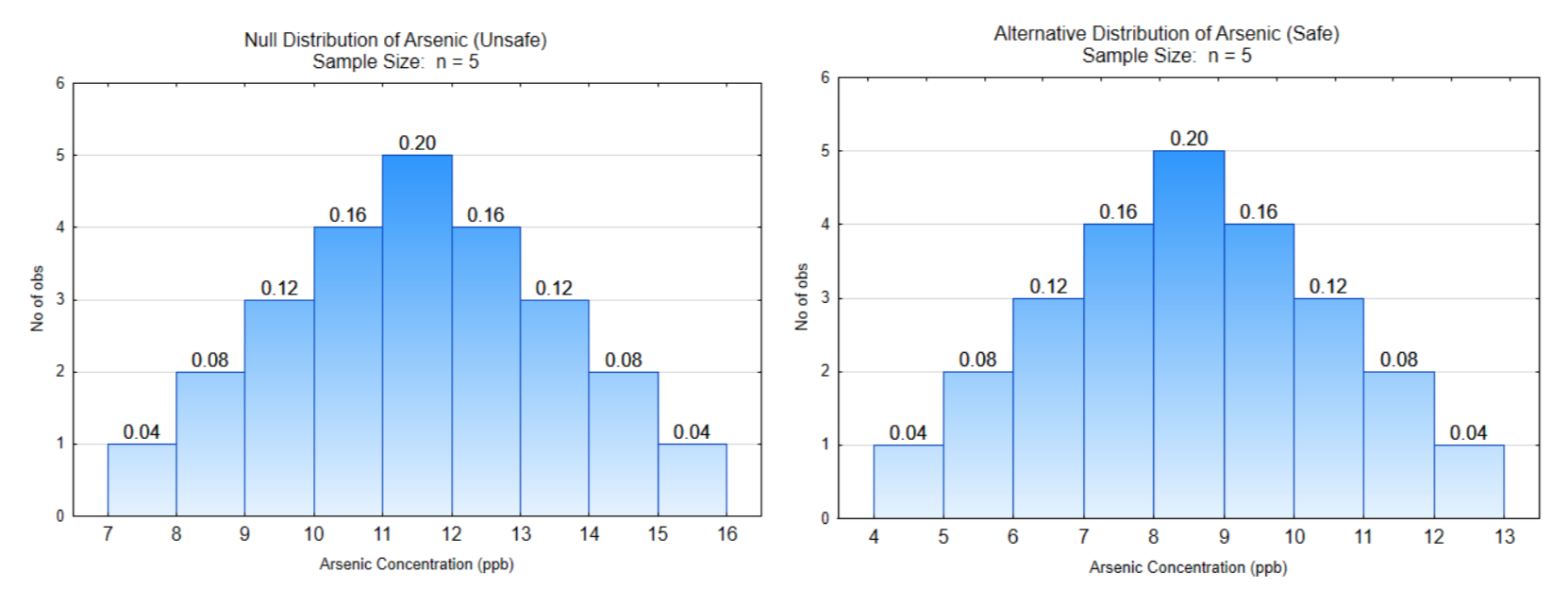
    2019-05-21 3.36.30.png

    Яке напрямок крайності?
    Показувати рядок рішення для обох дистрибутивів.
    Яке критичне значення?

    \(\alpha\)\(\beta\)Етикетка та влада

    Яка ймовірність\(\alpha\)?

    Яка ймовірність\(\beta\)?

    Що таке потужність?

    Що є наслідком помилки типу I?

    Що є наслідком помилки типу II?

    Дані: Що ви вибираєте з контейнера, який був переданий навколо класу

    Напишіть заключне речення:

    Яке рішення ви приймаєте щодо свого будинку та водопостачання?

    Елементарний тест гіпотез, приклад 2: Чи вважає більшість людей у США, що настав час для нової системи голосування?

    Брифінг: Система множинності голосування була використана в цій, і в інших країнах, з моменту формування демократії. Однак ця система призвела до домінування двох партій, які не обов'язково відображають думку громадян. Деякі країни, такі як Нова Зеландія, а також деякі штати та громади США прийняли інші системи голосування, які дозволяють краще представництво. Уявіть собі опитування, в якому людей запитували, чи вважають вони, що настав час змінити систему голосування як рішення вирішальної партизанства, яка зараз існує в США. Мета полягає в тому, щоб визначити, чи готова більшість виборців досліджувати альтернативні системи голосування. Гіпотези такі:\(H_0: p = 0.50\),\(H_1: p > 0.50\),\(\alpha = 0.07\).

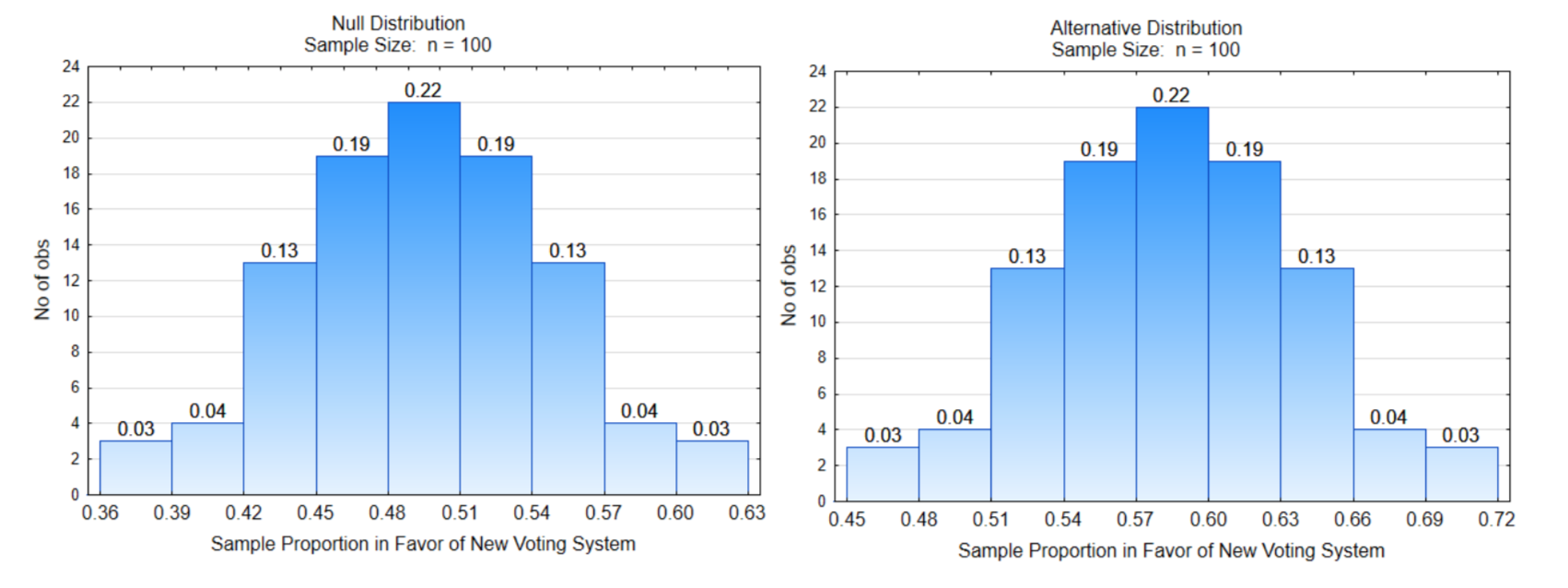
    2019-05-21 3.38.58.png

    Яке напрямок крайності?
    Показувати рядок рішення для обох дистрибутивів.
    Яке критичне значення?

    \(\alpha\)\(\beta\)Етикетка та влада

    Яка ймовірність\(\alpha\)?

    Яка ймовірність\(\beta\)?

    Що таке потужність?

    Що є наслідком помилки типу I?

    Що є наслідком помилки типу II?

    Дані: 54 з 100 виборців хотіли вивчити альтернативні системи голосування.

    Що таке пропорція вибірки?

    Напишіть заключне речення:

    Розділ 2 Дизайн таблиць

    1. Прагнучи визначити, яка стратегія найбільш ефективна для схуднення, дослідник випадковим чином відносить суб'єктів до однієї з чотирьох груп. Одна група (фізичні вправи) буде задіяна в регулярній програмі вправ, друга група буде годувати збалансованим харчуванням (їжею), але з відповідними розмірами порцій, третя група (фізичні вправи і харчування) буде використовувати як програму вправ, так і збалансовану дієту, тоді як четверта група (без змін) не змінить свій раціон або вправи.
      Дослідження Дизайн Таблиця
      Дослідницьке питання:
      Тип дослідження Спостережне дослідження
      Спостережний експеримент
      Маніпулятивний експеримент
      Що таке змінна відповіді?
      Який параметр буде обчислюватися? Середня пропорція
      Перерахуйте потенційні змішані змінні.
      Групування/пояснювальні змінні 1 (якщо є) Рівні:
    2. Люди збуджуються, коли молодий спортсмен досягає великого успіху, але завжди є питання про те, чи найкращі спортсмени коледжу були насправді серед кращих молодих спортсменів. Якщо інтерв'ю починаються спортсменів університетів з дивізіону 1 шкіл були зроблені, і їх запитали, якщо вони вважаються вищим спортсменом як 10 річний у своєму виді спорту, чи буде пропорція, яка була успішною, як маленька дитина, відрізнятися для чоловіків і жінок?
      Дослідження Дизайн Таблиця
      Дослідницьке питання:
      Тип дослідження Спостережне дослідження
      Спостережний експеримент
      Маніпулятивний експеримент
      Що таке змінна відповіді?
      Який параметр буде обчислюватися? Середня пропорція
      Перерахуйте потенційні змішані змінні.
      Групування/пояснювальні змінні 1 (якщо є) Рівні:

    Глава 2 Випадкові числа

    1. Буде зроблено опитування в нашому коледжі. Адміністрація очікує різних відповідей від бігових стартових студентів, традиційних студентів, що повертаються студентів та ветеранів. Вибірка буде проводитися з кожної з цих груп.

    Який метод відбору проб використовується?

    Якщо є 1320 ветеранів (1-1320), які числа перших 3 випадково вибраних ветеранів, якщо використовується значення насіння 3?

    2. Дані часових рядів будуть обрані з інтервалом 5 років, щоб дані були незалежними. Які цифри перших 3 випадково вибраних років даних, якщо перший рік даних - 1960? Використовуйте значення насіння 4.

    Глава 2 Порівняння та контрастність методів вибірки

    Ім'я___________________________ Зусил_____/5 Відвідуваність ____/1 Всього ___/6

    Поточна дискусія у Вашингтоні полягає в тому, чи будувати термінали експорту вугілля, щоб вугілля, видобуте в Монтані та Вайомінгу, можна було відправляти поїздом до узбережжя Вашингтона, Орегону чи Британської Колумбії, а потім експортувати до Азії. Деякі проблеми включають тривалі поїзди, які будуть постійним порушенням руху, вугільний пил з поїздів буде забруднювати повітря поблизу залізничних ліній, забруднення води, яке знищить рибальську та рибну промисловість, і занепокоєння, що вугілля сприятиме змінам клімату. Припустимо, що цільова група з 100 осіб з Айдахо, Вашингтона, Орегону та Британської Колумбії збирається, щоб визначити регіональну політику для цієї ситуації. Цільова група складається з державних службовців (G) та громадських громадян (C). Їм усім присвоєно номер від 1 до 100. Весь відбір проб буде проводитися з заміною. Це означає, що ви можете використовувати одне і те ж число двічі протягом одного методу вибірки. Ця діяльність призначена для того, щоб ви могли порівнювати та протиставити 4 методи вибірки.

    Група 1
    Айдахо    		 Група 2
    Вашингтон    		 Група 3
    Орегон    		 Група 4
    Британська Колумбія
    1 -С Без вугілля 23 -Г Без вугілля 49 -Г Термінали 71 -С Термінали
    2 -С Термінали 24 -С Термінали 50 -Г Без вугілля 72 -Г Термінали
    3 -С Термінали 25 -Г Без вугілля 51 -Г Без вугілля 73 -С Без вугілля
    4 -С Термінали 26 -Г Без вугілля 52 -Г Без вугілля 74 -Г Термінали
    5 -С Без вугілля 27 -С Термінали 53 -С Без вугілля 75 -С Термінали
    6 -С Термінали 28 -Г Без вугілля 54 -С Термінали 76 -С Термінали
    7 -С Термінали 29 -Г Без вугілля 55 -Г Без вугілля 77 -С Термінали
    8 -Г Без вугілля 30 -Г Без вугілля 56 -С Без вугілля 78 -Г Термінали
    9 -Г Термінали 31 -С Без вугілля 57 -Г Без вугілля 79 -Г Термінали
    10 -Г Без вугілля 32 -С Термінали 58 -Г Без вугілля 80 -С Термінали
    11 -С Термінали 33 -Г Термінали 59 -Г Без вугілля 81 -С Без вугілля
    12 -Г Без вугілля 34 -Г Термінали 60 -С Без вугілля 82 -Г Термінали
    13 -Г Термінали 35 -Г Термінали 61 -С Термінали 83 -Г Термінали
    14 -Г Без вугілля 36 -Г Термінали 62 -Г Без вугілля 84 -С Без вугілля
    15 -Г Термінали 37 -С Термінали 63 -С Без вугілля 85 -С Без вугілля
    16 -Г Без вугілля 38 -Г Термінали 64 -С Термінали 86 -Г Термінали
    17 -С Термінали 39 -С Термінали 65 -С Термінали 87 -С Без вугілля
    18 -Г Без вугілля 40 -Г Без вугілля 66 -Г Без вугілля 88 -С Термінали
    19 -Г Термінали 41 -Г Без вугілля 67 -Г Термінали 89 -Г Без вугілля
    20 -Г Термінали 42 -Г Термінали 68 -Г Без вугілля 90 -Г Без вугілля
    19 -С Термінали 43 -Г Без вугілля 69 -С Термінали 91 -Г Без вугілля
    22 -Г Без вугілля 44 -С Без вугілля 70 -С Термінали 92 -С Термінали
    45 -С Без вугілля 93 -Г Без вугілля
    46 -С Без вугілля 94 -С Без вугілля
    47 -Г Без вугілля 95 -Г Без вугілля
    48 -Г Без вугілля 96 -Г Термінали
    97 -Г Термінали
    98 -С Термінали
    99 -С Термінали
    100 Г Термінали

    1. Простий випадковий зразок

    Використовуйте свій калькулятор з насінням 23, щоб випадковим чином вибрати зразок розміром 10. Найменше число - 1, а найбільше - 100. Перерахуйте вибрані номери, а потім визначте частку зразка, яка знаходиться проти вугільних терміналів (No Coal).

    Номер: _____, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,

    Н або Т _____, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,

    Пропорція, яка проти вугільних терміналів:\(\hat{p} =\) _____

    2. Стратифікований випадковий зразок

    Скористайтеся калькулятором з насінням 13. Низький - 1, а високий - 100. Помістіть випадкові числа у відповідні пласти. Коли шар заповнений, ігноруйте інші числа, які належать до нього.
    Громадяни: Кількість _____, _____, _____, _____, _____, _____,

    Н або Т _____, _____, _____, _____, _____, _____,

    Уряд: Кількість _____, _____, _____, _____, _____, _____,

    Н або Т _____, _____, _____, _____, _____, _____,

    Пропорція (використання громадян та державних службовців разом узятих), що проти вугільних терміналів: \(\hat{p} =\)_____

    3. Систематична випадкова вибірка

    Використовуйте метод вибірки 1 в K, з k = 10, щоб випадково вибрати зразок розміром 10. Щоб визначити перше вибране число, скористайтеся калькулятором з насінням 18, низьким 1 і високим 10. Визначте частку зразка, яка знаходиться проти вугільних терміналів.

    Номер: _____, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,

    Н або Т _____, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,

    Пропорція, яка проти вугільних терміналів:\(\hat{p} =\) _____

    4. Кластерна вибірка

    Скористайтеся калькулятором із значенням насіння 33, щоб випадковим чином вибрати одну з груп (1-4). Яку групу вибрано? _____________. Яка частка вибірки вибраної групи проти вугільних терміналів? \(\hat{p} =\)_____

    Глава 3 Гістограми та графіки коробки

    Ім'я___________________________ Зусил_____/5 Відвідуваність ____/1 Всього ___/6

    Результати іспиту з глав 2 і 3 з одного класу статистики наведені в таблиці нижче. Цифри представляють відсоток можливих балів, які студент заробив.

    76.8 91.5 98.8 97.6 76.8 93.9 57.3 86.6 90.2
    93.9 93.9 82.9 92.7 89.0 72.0 57.3 93.9 92.7
    93.9 81.7 63.4 68.3 85.4 50.0 84.1 90.2 86.6
    97.6 84.1 81.7 95.1 87.8 75.6 92.7 73.2 91.5

    Низьке значення ___________ Високе значення _____________

    Зробіть розподіл частот. Використовуйте інтервальні позначення для меж [нижня, верхня).

    Заняття

    Зробіть гістограму. Позначте повністю.

    Скористайтеся калькулятором, щоб заповнити таблицю нижче, ввівши вихідні дані в списки.

    сторінка 266 зображення 8740176

    Середнє

    Стандартне відхилення Sx

    		 сторінка 266 зображення 156002816

    Мінімум

    		 сторінка 266 зображення 156003584

    Q1

    Медіана

    		 сторінка 266 зображення 156017088

    Q3

    Максимум

    		 сторінка 266 зображення 156021888сторінка 266 зображення 8736704

    Зробіть коробочку змови. Позначте повністю.

    Глава 4 Теорія висновків

    Питання 2: Чи більше 70% американців п'ють чай (гарячий або крижаний)?

    а) Напишіть свою нульову та альтернативну гіпотезу:

    б. знайти P (S): с. знайти P (F):

    d Якби ви взяли вибірку з 7 чоловік, яка ймовірність точного замовлення буде SFSSFSS? Тобто знайти П (SFSSFSS).

    е Скільки комбінацій існує на 5 успіхів у вибірці з 7 чоловік?

    f Яка ймовірність того, що ви отримаєте 5 успіхів у вибірці з 7 людей?

    м Складіть біноміальний розподіл за кількістю успіхів у вибірці з 7 осіб.

    2019-05-21 4.25.41 пнг

    h Яке середнє і стандартне відхилення для цього розподілу?

    т.е. закінчити заключне речення, якщо було 5 успіхів у вибірці з 7 чоловік. На рівні 5% значущості частка американців, які п'ють чай ________________________________________________________________________________________________________________________________________

    Глава 4 Теорія висновків - Тестування гіпотез

    Жителі північного заходу Тихого океану часто стурбовані питанням стійкості. Якщо опитування 400 людей на північному заході Тихого океану призвело до 296, які сказали, що роблять вибір, грунтуючись на стабільності, то перевірте гіпотезу про те, що понад 67% людей у цьому регіоні роблять вибір, грунтуючись на стабільності.

    Перевірте гіпотези (\(H_0: p = 0.67\)\(H_1: p > 0.67\)) за допомогою трьох різних методів і рівня значущості 0,05. Для кожного методу вас запитають, яка гіпотеза підтримується.

    1а. Біноміальний розподіл: Використовуйте біноміальний розподіл для обчислення точного p-значення на основі даних (296 з 400).

    ______________________________ ___________________
    Калькулятор введення р-значення

    Яку гіпотезу підтверджують дані? Виберіть 1:\(H_0\)\(H_1\)

    1б. Нормальне наближення: Використовуйте нормальне наближення до біноміального розподілу для обчислення наближеного p-значення на основі даних (296 з 400). Надайте запитувану інформацію.

    \(\mu = np = \),\(\sigma = \sqrt{npq} =\)

    Формула Підстановка z значення p-значення

    Яку гіпотезу підтверджують дані? Виберіть 1:\(H_0\)\(H_1\)

    1с. Розподіл вибірки для пропорцій вибірки: Знайдіть p-значення, використовуючи пропорції вибірки для даних (296 з 400). Надайте запитувану інформацію.

    Пропорція зразка

    Формула Підстановка z значення p-значення

    Яку гіпотезу підтверджують дані? Виберіть 1:\(H_0\)\(H_1\)

    Студент UC Santa Barbara (http://www.culturechange.org/cms/content/view/704/62/) зробив деякі дослідження пластикових червоних чашок, які люди використовують для напоїв на вечірках. Ці чашки виготовлені з полістиролу, який не можна переробляти в Санта-Барбарі. Багато чашок потрапляють на звалище, але деякі опиняються в океані. У сусідньому коледжному містечку Isla Vista дослідник підрахував, що середня кількість чашок, використовуваних на людину на рік, становила 58. Припустимо, стандартне відхилення дорівнює 8.

    Прагнучи змінити культуру, припустимо, що освітня кампанія була використана для зменшення кількості червоних чашок, заохочуючи придбання напоїв у банках (оскільки вони можуть бути перероблені). Щоб визначити, чи це ефективно, випадкова вибірка з 16 студентів буде відстежувати кількість червоних чашок, які вони використовують протягом року. Гіпотези, які будуть перевірені:\(H_0: \mu = 58\)\(H_1: \mu < 58\)\(\alpha = 0.05\)

    2а. Що означає розподіл відбору проб засобів? \(\mu_{\bar{x}}\)________

    2б. Що таке стандартне відхилення розподілу вибірки засобів? \(\sigma_{\bar{x}}\)_________

    2c. Намалюйте і позначте нормальний розподіл, що показує середнє і перші три стандартні відхилення (стандартні помилки) з кожного боку середнього для розподілу вибіркових засобів 16 учнів.

    2d, Перевірте гіпотезу, якщо середнє значення вибірки 16 студентів становить 55, використовуючи рівень значущості\(\alpha = 0.05\).

    Формула Підстановка z значення p-значення

    2е. Виходячи з результатів цього експерименту, чи відбулося зменшення використання червоних чашок? Виберіть 1: Так Ні

    Розділи 5 та 6 Змішана практика з перевіркою гіпотез та довірчими інтервалами

    Для кожної задачі надайте гіпотези та перевірте гіпотези, обчисливши статистику тесту та p-значення. Заповніть всі пропуски в наступному реченні. Також дайте відповідь калькулятора в дужках для тестової статистики та p-значення. Це не буде виправлено або оцінено, але допоможе підготувати вас до іспиту.

    1. Студент прочитав, що в районі затоки Каліфорнії середня людина виробляє 2 фунта сміття в день. Студентка вважала, що вона виробляє менше цього, але хотіла перевірити свою гіпотезу статистично. Вона збирала дані за 10 випадково вибраних днів. Використовувати\(\alpha = 0.05\).

    2.0 2.3 1.9 1.9 2.3
    1.2 2.3 2.1 1.7 1.8

    \(H_0:\)

    \(H_1:\)

    Що таке зразок означає? Зразок Середнє __________
    Що таке стандартне відхилення вибірки? Зразок стандартного відхилення______________

    Формула заміщення Тест Статистичне значення p-значення

    Калькулятор:

    Тестове статистичне значення p-значення

    Середня кількість сміття, що виробляється студентом щодня ___________ значно менше 2 фунтів (t = __________, р = _____________, n=_______________).

    Який 95% довірчий інтервал для кількості сміття, яке вона виробляє?

    Формула заміщення поля довірчого інтервалу похибки

    Довірчий інтервал калькулятора: __________________

    2. Прожитковий мінімум - це погодинна ставка, яку людина повинна заробляти, щоб утримувати свою сім'ю, якщо вони є єдиним постачальником і працюють повний робочий день. У 2005 році було підраховано, що 33% вакансій мали заробітну плату, яка була недостатньою (нижче прожиткового мінімуму). Дослідник хоче визначити, чи це все ще так. У вибірці з 460 робочих місць 207 мали неадекватну заробітну плату. Перевірте твердження, що частка робочих місць з недостатньою заробітною платою перевищує 0,33. Нехай\(\alpha =\) 0,01.

    \(H_0\)\(H_1\)

    Формула заміщення Тест Статистичне значення p-значення

    Калькулятор:

    Тестове статистичне значення p-значення

    Який довірчий інтервал 90% для частки робочих місць з недостатньою заробітною платою?

    Формула заміщення поля довірчого інтервалу похибки

    Довірчий інтервал калькулятора: __________________

    3. Припустимо, у вас було два різних способи потрапити в школу. Один шлях був на головних дорогах з великою кількістю світлофорів, інший - на задніх дорогах з невеликою кількістю світлофорів. Ви хотіли б знати, який шлях швидше. Ви випадковим чином вибираєте 6 днів для використання головної дороги та 6 днів для використання задніх доріг. Ваша мета полягає в тому, щоб визначити, чи середній час, який він займає на задній дорозі мкм, відрізняється від середнього часу на головній дорозі мкм. Дані представлені в таблиці нижче. Одиниці - хвилини. Припустимо, що розбіжності населення рівні. Оскільки розмір вибірки невеликий, ви вирішувативикористовувати рівень значущості\(\alpha = 0.1\).

    Назад Дорога 14.5 15,0 16.2 18.9 21.3 17.4
    Головна дорога 19.5 17.3 21.2 20.9 21.1 17,7

    Напишіть відповідні нульові і альтернативні гіпотези: Н0: _____________ Н1:______________

    Що означає зразок для кожного маршруту? Зворотній дорога______ Головна дорога ______

    Яке стандартне відхилення вибірки для кожного маршруту? Зворотній дорога______ Головна дорога ______

    Перевірте це за допомогою калькулятора

    Тестове статистичне значення p-значення

    Там _____________ суттєва різниця між взяттям задньої дороги і головної дороги (t = ______, р = ___________, n=_______).

    Який довірчий інтервал 99% для різниці середніх часів?

    Довірчий інтервал калькулятора: __________________

    Використовуйте ваш калькулятор згенерований довірчий інтервал для обчислення похибки ____________

    4. Деякі батьки спортсменів вікової групи вважають, що їхня дитина буде краще, якщо вони заплатять їм фінансову винагороду за успіх. Наприклад, вони можуть заплатити $5 за забив гол у футболі або $1 за найкращий час на зустрічі плавання. Аргумент проти оплати полягає в тому, що це контрпродуктивно і руйнує самомотивацію дитини. Чи відрізняється рівень відсіву дітей, які були виплачені, ніж у дітей, яким не платили? Нехай\(\alpha = 0.05\).

    Рівень відсіву дітей, яким було виплачено: 450 з
    510 Відсеву дітей, яким не заплатили: 780 з 930

    \(H_0\)\(H_1\)

    Перевірте це за допомогою калькулятора

    Тестове статистичне значення p-значення

    Який 95% довірчий інтервал різниці між рівнем відсіву дітей, які були виплачені, та дітьми, яким не виплачували? Нехай α = 0,05.

    Довірчий інтервал калькулятора: __________________

    Використовуйте ваш калькулятор згенерований довірчий інтервал для обчислення похибки ____________

    Глава 7 - Лінійний регресійний аналіз

    Завдання завдання 4 розглядає взаємозв'язок між населенням мегаполісу та кількістю патентів, вироблених у цій галузі. Нижче наведено розгорнутий зразок. Вона включає в себе більшу частину великих мегаполісів. Зробіть новий розкид ділянки. Використовуйте інший кольоровий маркер, щоб вказати Лас-Вегас і Фресно на цій ділянці розкиду. У домашньому завданні ці дві громади виглядали як викиди. Вони все ще?

    Використовуйте 5% -ний рівень значущості.

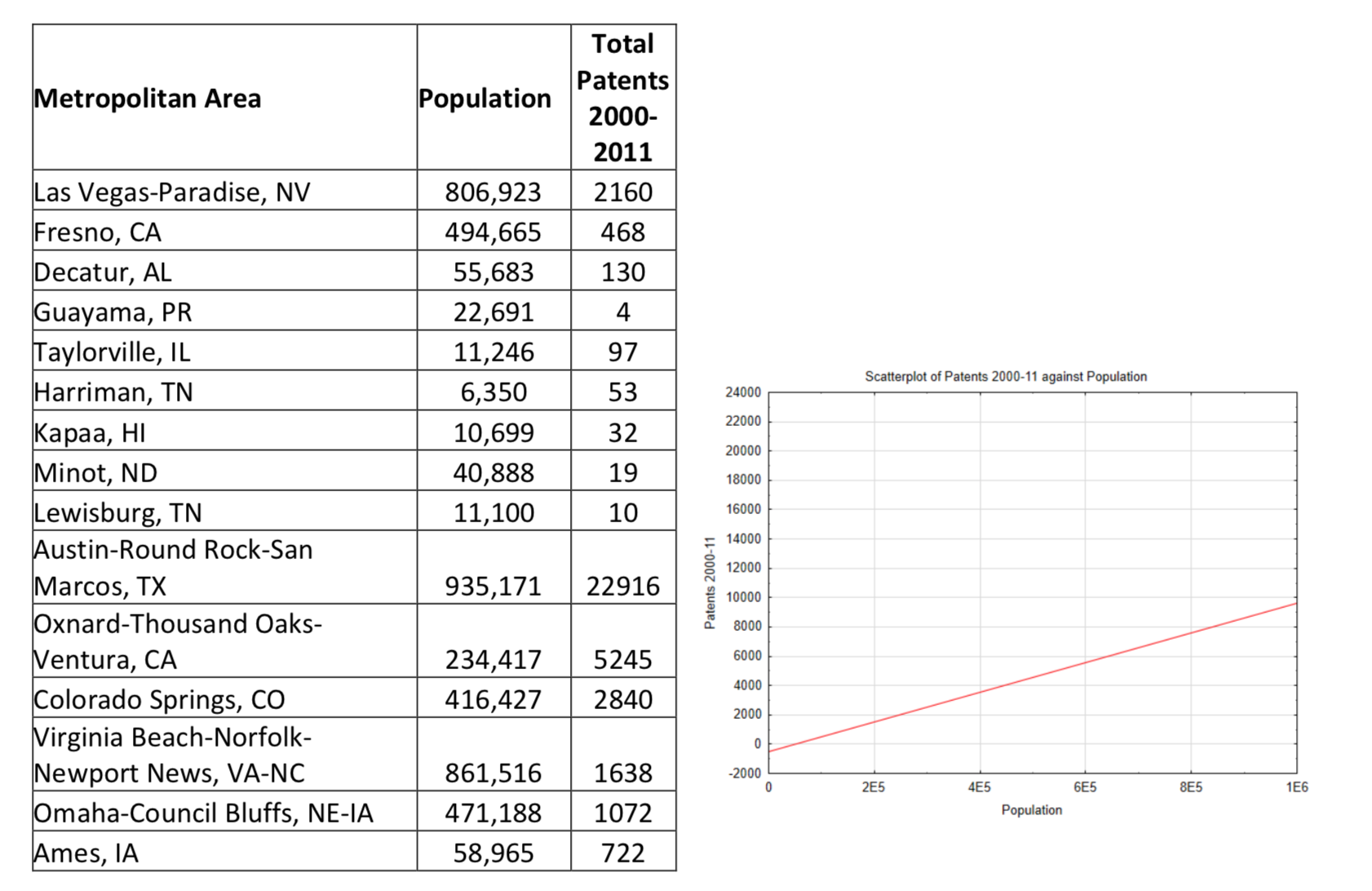
    2019-05-21 4.54.0.png

    Показати виходи калькулятора, включаючи кореляцію,\(r^2\) значення та рівняння лінії регресії (яка була зручно розміщена на графіку для вас). Напишіть статистичний висновок, а потім інтерпретуйте результати. Використовуйте рівень значущості 0,10.

    Кореляція ____________

    Коефіцієнт визначення (\(r^2\)значення) _______________

    Рівняння регресії _____________________

    Перевірка гіпотези заключного речення:

    Глава 7 —\(\chi ^2\)

    Якщо викладач змінює спосіб викладання курсу або використовує нову книгу, як вчитель знає, чи призвели зміни до кращого успіху для студентів? Один із способів - порівняти розподіл класів (A, B, C, нижче C) з тим, що відбувалося в минулих класах, припускаючи, що оцінки та оцінювання були подібними.

    Розподіл оцінок за минулі класи, які використовували перше видання «Основи статистичного міркування», показано в середній колонці таблиці нижче. Кількість учнів, які отримали кожен бал при використанні другого видання, наведено нижче.

    Сорт

    		 сторінка 275 зображення 155977216Пропорція

    Граф з другого видання

    A

    0,349

    		 сторінка 275 зображення 155977984

    16

    Б

    сторінка 275 зображення 155982208

    0,287

    сторінка 275 зображення 155986240    		 сторінка 275 зображення 155979712

    11

    C

    0,204

    7

    сторінка 275 зображення 155991232

    Нижче C

    0,160

    6
    сторінка 275 зображення 155825088сторінка 275 зображення 8707968

    Перевірте гіпотезу про те, що розподіл оцінок з другого видання відрізняється від розподілу з першого видання.
    Напишіть гіпотези:

    \(H_0\):
    \(H_1\):

    Який тест підходить для цієї проблеми?

    А. _______ Доброта придатності B. _______ Тест на незалежність C. _______ Тест на однорідність

    Перевірте гіпотезу, скориставшись таблицею нижче.

    Спостерігається Очікується \(O - E\) \((O - E)^2\) \(\dfrac{(O - E)^2}{E}\)
    \(\chi^2 =\)

    Напишіть заключне речення:

    Який із наведених нижче висновків підтверджують докази?

    _____Друге видання призвело до значно покращеного розподілу оцінок

    _____Друге видання призвело до суттєвого погіршення розподілу оцінок

    _____Друге видання, схоже, не вплинуло на розподіл оцінок

    Цю проблему можна було б зробити по-іншому, якби вам сказали кількість людей, які отримали кожен клас, використовуючи перше видання.

    Сорт

    		 сторінка 276 зображення 155765760

    Граф з першого видання

    		 сторінка 276 зображення 8885840

    Граф з другого видання
    сторінка 276 зображення 155772480

    A

    		 сторінка 276 зображення 155764224

    174

    		 сторінка 276 зображення 155723328

    16

    Б

    143

    11

    C

    сторінка 276 зображення 155774400

    102

    сторінка 276 зображення 155775552

    7

    сторінка 276 зображення 155771520

    Нижче C

    80

    6

    Перевірте гіпотезу про те, що розподіл оцінок з другого видання відрізняється від розподілу з першого видання.
    Напишіть гіпотези:

    \(H_0:\)
    \(H_1:\)

    Який тест підходить для цієї проблеми?

    А. _______ Доброта придатності B. _______ Тест на незалежність C. _______ Тест на однорідність

    Використовуйте матрицю і\(\chi^2\) тест на калькуляторі, щоб перевірити гіпотезу.