4: Інференційна теорія
- Page ID
- 97372
До виборів опитувальники опитуватимуть приблизно 1000 осіб і на основі їх результатів спробують спрогнозувати результат виборів. На перший погляд, це має здатися абсурдом, що думки 1000 можуть дати будь-яке свідчення про думку 100 000 000 виборців на національних президентських виборах. Так само взяття 100 або 1000 проб води з Puget Sound, коли це незначна кількість води порівняно із загальною кількістю постійно мінливої води в Звуку, має здатися недостатнім для прийняття рішення.
Мета цієї глави - розробити теорію, яка допомагає нам зрозуміти, чому відносно невеликий розмір вибірки насправді може призвести до висновків про набагато більшу кількість населення. Пояснення різне для категоричних і кількісних даних. Почнемо з категоричних даних.
Подорож, яку ви проберете через цей розділ, має кінцевий пункт призначення у формулі, яка в кінцевому підсумку буде використана для перевірки гіпотез. Хоча ви можете бути готові прийняти формулу, не беручи подорож, це буде подорож, яка надає значення формулі. Оскільки дані стохастичні, тобто схильні до випадковості, ймовірність відіграє вирішальну роль у цій подорожі.
Наша подорож починається з концепції висновку. Висновок означає, що невелика кількість спостережуваної інформації використовується для того, щоб зробити загальні висновки. Наприклад, ви можете відвідати бізнес і отримати видатне обслуговування клієнтів, з якого ви робите висновок, що цей бізнес піклується про своїх клієнтів. Висновок використовується при перевірці гіпотези. Невеликий обсяг інформації, зразок, використовується для того, щоб зробити висновок, або зробити щось про все населення.
Теорія починається з знаходження ймовірності отримання тієї чи іншої вибірки і в кінцевому підсумку закінчується створенням розподілів всіх результатів вибірки, які можливі, якщо нульова гіпотеза істинна. Для кожного кроку 7-крокової подорожі будуть зроблені відступи, щоб дізнатися про конкретні правила ймовірності, які сприяють теорії висновків.
Перед початком роботи необхідно уточнити деяку термінологію, яка буде використовуватися. Незалежно від питання, яке задається, якщо воно виробляє категоричні дані, ці дані будуть визначені загалом як успіх чи невдача, без використання цих термінів у звичному порядку. Наприклад, дослідник, який висуває гіпотезу про частку людей, які є безробітними, вважав би безробітним успіхом зі статистичної точки зору, а працевлаштований як невдачу, хоча це суперечить тому, як це розглядається в реальному світі. Таким чином, успіх - це значення даних, про які пишуться гіпотези, а невдача - альтернативне значення даних.
Брифінг 4.1 Самохідні автомобілі
Google, як і більшість автомобільних компаній, розробляють самохідні автомобілі. Ці автономні автомобілі не повинні мати водія і вважаються менш імовірними, що потрапляють в аварію, ніж автомобілі, якими керують люди. Такі автомобілі, як ці, як очікується, будуть доступні для громадськості приблизно в 2020 - 2025 роках. Є багато питань, на які необхідно відповісти, перш ніж ці автомобілі стануть доступними. Одним з таких питань є визначення того, хто несе відповідальність у разі ДТП. Чи несе відповідальність власник автомобіля, хоча вони не керували автомобілем або несе відповідальність виробника, оскільки їх технологія не уникнула аварії? (mashable.com/2014/07/07/привід... -автомобілі-tipping- точки/, переглянутий липень 2014).
Крок 1 - Наскільки ймовірно, що конкретне значення даних є успішним?
Припустимо, дослідник хотів визначити частку громадськості, яка вважає, що власник несе відповідальність за аварію. У дослідника є гіпотеза, що частка становить понад 60%. В цьому випадку гіпотези будуть такими:
- \(H_0: p = 0.60\)
- \(H_1: p > 0.60\)
При зборі даних порядок, в якому вибираються одиниці або люди, визначає порядок, в якому збираються дані. В цьому випадку покладання відповідальності на власника буде вважатися успішним, а покладання відповідальності на виробника буде вважатися провалом. Якщо перша особа вважає, що власник несе відповідальність, друга людина вважає, що виробник несе відповідальність, третя особа вибирає виробника, четверта, п'ята та шоста люди вибирають власника як відповідальну сторону, тоді ми можемо перетворити цю інформацію на успіхи та невдачі, перерахувавши порядок, в якому дані були отримані як SFFSSS.
Стратегія, яка використовується для визначення того, яка з двох конкуруючих гіпотез краще підтримується, завжди припускає, що нульова гіпотеза вірна. Це критична точка, тому що якщо ми можемо припустити, що умова істинна, то ми можемо визначити ймовірність отримання нашого конкретного результату вибірки або більш екстремальних результатів. Це p-значення.
Однак перш ніж ми зможемо визначити ймовірність отримання такої послідовності, як SFFSSS, ми повинні спочатку знайти ймовірність отримання успіху. Для цього нам потрібно вивчити поняття ймовірності.
Відступ 1 - Ймовірність
Імовірність - це шанс того, що той чи інший результат трапиться, якщо процес повторюється дуже велика кількість разів. Його кількісно визначають шляхом ділення кількості сприятливих результатів на кількість можливих результатів. Це показано у вигляді формули:
\[P(A) = \dfrac{\text{Number of Favorable Outcomes}}{\text{Number of Possible Outcomes}}\]
де\(P(A)\) означає ймовірність якоїсь події під назвою\(A\). Ця формула передбачає, що всі результати однаково вірогідні, що і відбувається з хорошим випадковим процесом вибірки. Весь набір можливих результатів називається простором вибірки. Кількість можливих результатів збігається з кількістю елементів у вибірковому просторі.
Хоча мета цієї глави полягає в тому, щоб зосередитися на розробці теорії для перевірки гіпотез, кілька понять будуть пояснені спочатку з більш легкими прикладами.
Якщо ми хотіли знати ймовірність отримання хвоста, коли ми перевертаємо справедливу монету, то ми повинні спочатку розглянути простір зразка, який буде {H, T}. Оскільки в цьому вибірковому просторі є один елемент, який є сприятливим, а простір вибірки містить два елементи, ймовірність є\(p(tails) = \dfrac{1}{2}\).
Щоб знайти ймовірність отримання 4 при прокатці справедливої матриці, створимо простір зразка з шістьма елементами {1,2,3,4,5,6}, так як це можливі результати, які можна отримати при прокатці матриці. Щоб знайти ймовірність або прокатки 4, ми можемо підставити в формулу, щоб отримати\(P(4) = \dfrac{1}{6}\).
Більш складним питанням є визначення ймовірності отримання двох голів при гортанні двох монет або перевертання однієї монети двічі. Простір вибірки для цього експерименту є {HH, HT, TH, TT}. Імовірність дорівнює (HH) =\(\dfrac{1}{4}\). Імовірність отримання однієї голови і одного хвоста, в будь-якому порядку дорівнює (1 голова і 1 хвіст) =\(\dfrac{2}{4}\) =\(\dfrac{1}{2}\).
Імовірність завжди буде числом від 0 до 1, таким чином\(0 \le P(A) \le 1\). Імовірність 0 означає, що щось не може статися. Імовірність 1 - це впевненість.
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Якщо припустити, що нульова гіпотеза вірна, то частка людей, які вважають, що власник несе відповідальність, становить 0,60. Що це означає? Це означає, що якщо є рівно 100 осіб, то рівно 60 з них беруть на себе відповідальність власника, а 40 - ні.
Якщо наша мета - знайти ймовірність SFFSSS, то треба спочатку знайти ймовірність отримання успіху (власника). Якщо в населенні 100 осіб і 60 з них вибирають власника, то ймовірність вибору людини, яка вибирає власника, є\(P(owner) = \dfrac{60}{100} = 0.60\). Зверніть увагу, що ця ймовірність точно дорівнює пропорції, визначеної в нульовій гіпотезі. Це не випадковість, і це буде відбуватися щоразу, оскільки пропорція в нульовій гіпотезі використовується для генерації теоретичної сукупності, яка використовувалася для пошуку ймовірності. Першим важливим кроком у процесі тестування гіпотези є усвідомлення того, що ймовірність успіху будь-яких даних дорівнює пропорції, визначеної в нульовій гіпотезі, припускаючи, що вибірка проводиться з заміною, або що розмір популяції надзвичайно великий, так що видалення одиниця з населення не змінює ймовірність значної суми.
Приклад 1
- Якщо\(H_0: p = 0.35\), то ймовірність\(5^{\text{th}}\) значення успіху дорівнює 0,35.
- Якщо\(H_0: p = 0.82\), то ймовірність\(20^{\text{th}}\) значення успіху дорівнює 0,82.
Крок 2 - Наскільки ймовірно, що конкретне значення даних є помилкою?
Тепер, коли ми знаємо, як знайти ймовірність успіху, ми повинні знайти ймовірність невдачі. Для цього ми знову відступимо від правил ймовірності.
Відступ 2 - Імовірність A або B
Коли з популяції вибирається одна одиниця, може бути кілька можливих заходів, які можуть бути вжиті по ній. Наприклад, новий шматок техніки можна було б поставити в кілька марок автомобілів, а потім перевірити на надійність. Наведена нижче таблиця непередбачених ситуацій показує кількість автомобілів у кожній з категорій. Ці цифри фіктивні і ми будемо робити вигляд, що це все населення автомобілів, що розробляються.
| Hyundai | Nissan | Всього | ||
|---|---|---|---|---|
| Надійний | 80 | 75 | 90 | 245 |
| Не надійний | 25 | 10 | 20 | 55 |
| Всього | 105 | 85 | 110 | Гранд Всього 300 |
З цього ми можемо задати різноманітні питання ймовірності.
Якщо випадковим чином обраний один автомобіль, яка ймовірність того, що це Nissan?
\(P(Nissan) = \dfrac{85}{300} = 0.283\)
Якщо випадковим чином обраний один автомобіль, яка ймовірність того, що шматок техніки не був надійним?
\(P(not reliable) = \dfrac{55}{300} = 0.183\)
Якщо випадковим чином обраний один автомобіль, то яка ймовірність того, що це Hyundai або шматок техніки був надійним?
Це питання вводить слово «або», що означає, що автомобіль має ту чи іншу характеристику або обидві. Слово «або» використовується, коли робиться лише один вибір. Таблиця нижче повинна допомогти вам зрозуміти, як буде виведена формула.

Зверніть увагу, що значення 2 в стовпці Hyundai обведені, а три значення в рядку «Надійний» обведені, але що значення в комірці, що містить число 80, що представляє Hyundai і Relible, обводиться двічі. Ми не хочемо підраховувати ці конкретні автомобілі двічі, тому після додавання стовпця для Hyundai до рядка для Надійний, необхідно відняти комірку для Hyundai і Надійний, оскільки вона була підрахована двічі, але повинна бути зарахована лише один раз. Таким чином, рівняння стає:
P (Hyundai або надійний) = P (Hyundai) + P (Надійний) - P (Hyundai і надійний)
=\(\dfrac{105}{300} + \dfrac{245}{300} - \dfrac{80}{300} = \dfrac{270}{300} = 0.90\)
З цього ми узагальнимо формулу бути
\[P(A\ or\ B) = P(A) + P(B) - P(A\ and\ B).\]
Що буде, якщо ми скористаємося формулою для визначення ймовірності випадкового вибору автомобіля Nissan або Google?
Оскільки ці два критерії не можуть відбуватися одночасно, вони, як кажуть, є взаємовиключними. Отже, їх перетин дорівнює 0.
Р (Ніссан або Гугл) = Р (Ніссан) + Р (Гугл) — Р (Ніссан і Гугл)
=\(\dfrac{85}{300} + \dfrac{110}{300} - \dfrac{0}{300} = \dfrac{195}{300} = 0.65\)
Оскільки перетин дорівнює 0, це призводить до модифікованої формули для категоріальних значень даних, які є взаємовиключними.
\[P(A\ or\ B) = P(A) + P(B)\]
Це формула, яка представляє для нас першорядний інтерес для визначення того, як знайти ймовірність невдачі.
Якщо успіх і невдача - це тільки два можливих результату, і неможливо одночасно мати успіх і невдачу, то вони взаємовиключні. Крім того, якщо випадковий вибір зроблений, то впевнений, що це буде успіх або невдача. Речі, які є певними, мають ймовірність 1. Тому ми можемо записати формулу, використовуючи S і F як:
\(P(S\ or\ F) = P(S) + P(F)\)
або
\(1 = P(S) + P(F)\)
з невеликою алгеброю це стає
\[1- P(S) = P(F)\]
Це означає, що віднімання ймовірності успіху з 1 дає ймовірність невдачі. Імовірність невдачі називається доповненням ймовірності успіху.
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Нагадаємо, що початкова гіпотеза відповідальності при ДТП полягає в тому, що: Н0: р = 0,60. Ми встановили, що ймовірність успіху дорівнює 0,60. Імовірність невдачі дорівнює 0,40, оскільки вона є доповненням ймовірності успіху і 1 — 0,60 = 0,40.
Приклад 2
- Якщо\(H_0: p = 0.35\), то ймовірність\(5^{\text{th}}\) значення успіху дорівнює 0,35. Імовірність\(5^{\text{th}}\) значення відмови дорівнює 0,65.
- Якщо\(H_0: p = 0.82\), то ймовірність\(20^{\text{th}}\) значення успіху дорівнює 0,82. Імовірність\(20^{\text{th}}\) значення відмови дорівнює 0,18.
Крок 3 - Наскільки ймовірно, що зразок складається з певної послідовності успіхів і невдач?
Тепер ми знаємо, що ймовірність успіху ідентична пропорції, визначеній нульовою гіпотезою, і ймовірність невдачі є доповненням. Але ці ймовірності стосуються тільки одного виділення. Що відбувається, коли вибрано більше одного? Щоб знайти цю ймовірність, ми повинні вивчити останнє з правил ймовірності:
\[P(A\ and\ B) = P(A)P(B)\]
Відступ 3 - Р (А і В) = Р (А) Р (В)
Якщо зроблено два або більше виділень, слово «і» стає важливим, оскільки воно вказує на те, що ми шукаємо один результат для першого вибору та один результат для другого вибору. Ця ймовірність виявляється шляхом множення індивідуальних ймовірностей. Частина ключа до вибору цієї формули полягає у визначенні проблеми як проблеми «і». Наприклад, на початку цього розділу ми виявили ймовірність отримати дві голови при гортанні двох монет становить 0,25. Цю проблему можна розглядати як проблему «і», якщо запитати «яка ймовірність отримати голову при першому сальті і голову на другому сальто»? Використовуючи індекси 1 і 2 для представлення першого та другого сальто відповідно, ми можемо переписати формулу, щоб показати:
\(P(H_1\ and\ H_2) = P(H_1)P(H_2) = (\dfrac{1}{2})(\dfrac{1}{2}) = \dfrac{1}{4} = 0.25.\)
Припустимо, дослідник випадковим чином вибирає три машини. Яка ймовірність того, що буде по одній машині кожної з марок (Hyundai, Nissan, Google)?
| Hyundai | Nissan | Всього | ||
|---|---|---|---|---|
| Надійний | 80 | 75 | 90 | 245 |
| Не надійний | 25 | 10 | 20 | 55 |
| Всього | 105 | 85 | 110 | Гранд Всього 300 |
По-перше, оскільки вибираються три автомобілі, це слід визнати проблемою «і» і можна сформулювати P (Hyundai і Nissan і Google). Перш ніж ми зможемо визначити ймовірність, однак, є одне важливе питання, яке потрібно задати. Це питання полягає в тому, чи буде дослідник вибирати з заміною.
Якщо дослідник проводить відбір проб з заміною, то ймовірність може бути визначена наступним чином.
P (Хендай і Ніссан і Гугл) = Р (Хендай) П (Ніссан) П (Гугл) =
\((\dfrac{105}{300})(\dfrac{85}{300})(\dfrac{110}{300}) = 0.03636.\)
Зверніть увагу на незначну зміну ймовірності в результаті невикористання заміни.
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Ми зараз готові відповісти на питання про те, яка ймовірність того, що ми отримали б точну послідовність людей, якщо перша людина вважає, що власник несе відповідальність, друга людина вважає, що виробник несе відповідальність, третя особа вибирає виробника, четвертий, п'ятий і шостий люди все вибрати власника в якості відповідальної сторони. Оскільки вибрано шість людей, то це проблема «і» і може бути записана як P (S і F і F і S і S і S і S) або більш стисло, залишаючи слово «і», але зберігаючи його за підтекстом, ми пишемо P (SFFSSS). Пам'ятайте, що P (S) = 0,6 і P (F) = 0,4
Р (СФССС) = Р (С) Р (Ф) Р (Ф) Р (С) Р (С) Р (С) = (0,6) (0,4) (0,4) (0,6) (0,6) (0,6) = 0,0207.
Підводячи підсумок, якщо нульова гіпотеза вірна, то 60% людей вважають, що власник несе відповідальність за нещасні випадки. При цих умовах, якщо береться проба з шести чоловік, з заміною, то ймовірність отримання цієї точної послідовності успіхів і невдач становить 0,0207.
Крок 4 - Наскільки ймовірно, що зразок буде містити певну кількість успіхів?
Знання ймовірності точної послідовності успіхів і невдач не особливо важливо саме по собі. Це крок до питання більшого значення — яка ймовірність того, що чотири з шести випадково відібраних людей (із заміною) повірять власнику відповідальність? Це важливий перехід у мисленні, яке робиться. Це перехід від мислення про конкретну послідовність до роздумів про кількість успіхів у вибірці.
Коли дані збираються, дослідники не дбають про порядок даних, лише скільки успіхів було у вибірці. Нам потрібно знайти спосіб переходу від ймовірності отримання певної послідовності успіхів і невдач, таких як SFFSSS, до знаходження ймовірності отримання чотирьох успіхів з вибірки розміром 6. Цей перехід використовуватиме комутативну властивість множення, правило P (A або B) та комбінаторику (методи підрахунку).
В кінці кроку 3 ми виявили, що P (SFFSSS) = 0,0207.
- Як ви думаєте, якою буде ймовірність P (SSFSF)?
- Як ви думаєте, якою буде ймовірність P (SSSSFF)?
Відповідь на обидва ці питання становить 0.0207, оскільки всі ці послідовності містять 4 успіхи та дві невдачі, і оскільки ймовірність виявляється шляхом множення ймовірностей успіху та невдачі в послідовності, а оскільки множення є комутативним (порядок не має значення), то
(0.6) (0.4) (0.4) (0.6) (0.6) = (0.6) (0.6) (0.6) (0.6) (0.4) (0.6) (0.6) = (0,6) (0,6) (0.6) (0.4) = 0.020736.
Якщо питання зараз змінюється від того, яка ймовірність послідовності, на те, яка ймовірність 4 успіхів у вибірці розміру 6, то ми повинні розглянути всі різні способи, за допомогою яких можна організувати чотири успіхи. Ми можемо отримати 4 успіхи, якщо послідовність нашого вибору - SFFSSSS або SSSFSF або SSSSFF або численні інші можливості. Оскільки ми проводимо вибірку один раз і тому, що є багато можливих результатів, які ми могли б мати, це проблема «або», яка використовує розширену версію формули P (A або B) = P (A) + P (B). Це можна записати як:
Р (4 з 6) = П (СФФСССС або ССССФФ або ССССФФ або...) = П (СФФСССС) + П (ССССФСФ) + П (ССССССФ) +...
Іншими словами, ми можемо додати ймовірність кожного з цих замовлень. Однак, оскільки ймовірність кожного з цих замовлень однакова (0.0207), то цей процес був би набагато швидше, якби ми просто помножили 0,0207 на кількість можливих замовлень. Питання, на яке ми повинні відповісти тоді, скільки способів організувати чотири успіхи та 2 невдачі? Щоб відповісти на це, ми повинні вивчити область комбінаторики, які забезпечують різні методи підрахунку.
Відступ 4 — Комбінаторика
Дослідники, що проектують автомобілі, порівнюватимуть різні технології, щоб побачити, яка працює краще. Припустимо, для автомобіля доступні дві марки відеокамери. Скільки різних пар можливо?
Деревоподібна діаграма може допомогти пояснити це.
Створення діаграми дерева для відповіді на такі питання може бути нудним, тому простіший підхід полягає у використанні основного правила підрахунку, яке стверджує, що якщо є M варіантів для одного вибору, який повинен бути зроблений, і N варіантів для другого вибору, який повинен бути зроблений, то існують унікальні комбінації MN. Один із способів показати це - намалювати та позначити лінію для кожного вибору, який потрібно зробити, і на рядку написати кількість доступних варіантів. Помножте числа.
_______2_________ ____3_________ = 6
Відео Автомобілі
Це говорить вам, що існує шість унікальних комбінацій для однієї камери та однієї марки автомобіля.
Якщо дослідники мають 4 випробувальних транспортних засобів, які будуть їздити по автостраді як конвой, а кольори транспортних засобів - синій, червоний, зелений та жовтий, скільки способів можна замовити ці автомобілі в конвою?
Щоб відповісти на це питання, подумайте про це як про те, щоб зробити чотири варіанти вибору, який колір автомобіля перший, другий, третій, четвертий. Намалюйте лінію для кожного вибору і на рядку напишіть кількість доступних варіантів, а потім перемножте ці числа. Існує чотири варіанти першого автомобіля. Після того, як цей вибір зроблений, залишається три варіанти для другого автомобіля. Коли цей вибір зроблений, залишається два варіанти для третього автомобіля. Після того, як вибір зроблений, залишається тільки один варіант, доступний для кінцевого автомобіля.
4 3 2 1 = 24 унікальних замовлень
Перший автомобіль Другий автомобіль Третій автомобіль Четвертий автомобіль
Приклади деяких з цих унікальних замовлень включають: синій, червоний, зелений та жовтий,
червоний, синій, зелений та жовтий,
зелений, червоний, синій та жовтий
Кожна унікальна послідовність називається перестановкою. Таким чином, в даній ситуації існує 24 перестановки.
Спосіб знаходження кількості перестановок при використанні всіх доступних елементів називається факторіал. У цій задачі використовуються всі чотири автомобілі, тому кількість перестановок дорівнює 4 факторіалу, який символічно відображається як 4!. 4! засоби (4) (3) (2) (1). Щоб бути більш загальним,
\[n! = n(n - 1)(n - 2)... 1\]
Перестановки також можна знайти, коли використовується менше елементів, ніж доступно. Наприклад, припустимо, що дослідники використовуватимуть лише два з чотирьох автомобілів. Скільки різних замовлень можливо? Наприклад, синій автомобіль, за яким слідує зелений автомобіль, - це інший порядок, ніж зелений автомобіль, за яким слідує синій автомобіль. Ми можемо відповісти на це питання двома способами (і, сподіваємось, отримаємо однакову відповідь обома способами!). Перший спосіб полягає у використанні основного правила підрахунку та намалюйте дві лінії для вибору, який ми робимо, поставивши кількість варіантів, доступних для кожного вибору на лінію, а потім множивши.
4 3 = 12 перестановок
Перший автомобіль другий автомобіль
Приклади можливих перестановок включають:
Синій, зелений, зелений, синій, синій, червоний жовтий, зелений
Другий підхід полягає у використанні формули для перестановок, коли вибране число менше або дорівнює кількості доступних. У цій формулі r представляє кількість вибраних елементів, n - кількість доступних елементів.
\[nPr = \dfrac{n!}{(n - r)!}\]
Для цього прикладу n дорівнює 4 і r дорівнює 2 так з формулою ми отримуємо:
\(_4P_2 = \dfrac{4!}{(4 - 2)!} = \dfrac{4!}{2!} = \dfrac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1} = 4 \cdot 3 = 12\)перестановки.
Зверніть увагу,\(4 \cdot 3\) що кінцевий продукт такий же, як у нас при використанні основного правила підрахунку. Знаменник терміну (n-r)! використовується для скасування непотрібних числівників термінів.
Для перестановок важливий порядок, але що робити, якщо порядок не важливий? Наприклад, що робити, якби ми хотіли знати, скільки пар автомобілів різних кольорів можна поєднати, якщо нас не хвилює порядок, в якому вони їхали. В такому випадку нас цікавлять комбінації. У той час як синій, зелений і зелений, синій представляють дві перестановки, вони представляють лише одну комбінацію. Завжди буде більше перестановок, ніж комбінацій. Кількість перестановок для кожної комбінації дорівнює r!. Тобто, коли вибрано 2 авто, їх 2! перестановки для кожної комбінації.
Щоб визначити кількість комбінацій, якщо вибрано два з чотирьох автомобілів, ми можемо розділити загальну кількість перестановок на кількість перестановок на комбінацію.
\(Number\ of\ combinations = Number\ of\ permutations (\dfrac{1\ Combination}{Number\ of\ Permutations})\)
Використовуючи подібні позначення, які використовувались для перестановок (nPR), комбінації можуть бути представлені за допомогою nCr, тому рівняння можна переписати як
\[\begin{array} {rcl} {nCr} &= & {nPr(\dfrac{1}{r!})\ or} \\ {nCr} &= & {\dfrac{n!}{(n - r)!} (\dfrac{1}{r!})} \\ {nCr} &= & {\dfrac{n!}{(n - r)!r!}} \end{array}\]
Альтернативний спосіб розробки цієї формули, яка може бути використана для більших розмірів вибірки, які містять успіхи та невдачі, - вважати, що кількість перестановок дорівнює n! в той час як кількість перестановок для кожної комбінації дорівнює r! (н-р)!. Наприклад, у вибірці розміром 20 з 12 успіхами і 8 невдачами, їх 20! перестановки успіхів і невдач в поєднанні з 12! перестановки успіхів і 8! перестановки збоїв для кожної комбінації. Таким чином,
\(Number\ of\ combinations = 20!(\dfrac{1\ Combination}{12!8!}) = \dfrac{20!}{12!8!}\ or\ as\ a\ formula:\)
\(Number\ of\ combinations = n!(\dfrac{1\ Combination}{r!(n - r)!}) = \dfrac{n!}{r!(n - r)!}\ or\ \dfrac{n!}{(n - r)!r!}\).
Для нашого прикладу про кольори автомобіля ми маємо:
\(_4C_2 = \dfrac{4!}{(4 - 2)! 2!} = \dfrac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1 \cdot 2 \cdot 1} = 6\)комбінації.
Ця послідовність концепцій комбінаторики досягла наміченої мети в тому, що інтерес полягає в кількості комбінацій успіхів і невдач є для заданої кількості успіхів у вибірці. Тепер повернемося до проблеми відповідальності за нещасні випадки.
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Нагадаємо, що було відібрано 6 осіб і 4 вважали, що господар повинен нести відповідальність. Ми побачили, що ймовірність будь-якої послідовності з 4 успіхів і 2 невдач, таких як SFFSSSS або SSSFSF або SSSSFF дорівнює 0.0207, якщо нульова гіпотеза дорівнює p = 0,60. Якби ми знали кількість комбінацій цих 4 успіхів і 2 невдач, ми могли б помножити це число разів ймовірність будь-якої конкретної послідовності, щоб отримати ймовірність 4 успіхів у вибірці розміру 6.
Використовуючи формулу для nCR, отримуємо:\(_6C_4 = \dfrac{6!}{(6 - 4)!4!} = 15\) комбінації.
Тому ймовірність 4 успіхів у вибірці розміром 6 дорівнює 15*0,020736 = 0,31104. Це означає, що якщо нульова гіпотеза p=0.60 вірна і запитують шість людей, існує ймовірність 0.311, що четверо з цих людей повірять, що власник несе відповідальність.
Тепер ми готові зробити перехід до дистрибутивів. Наступна таблиця підсумовує нашу подорож до цього моменту.
| Крок 1 | Використовуйте нульову гіпотезу для визначення P (S) для будь-якого виділення, припускаючи заміну. |
| Крок 2 | Використовуйте правило P (A або B), щоб знайти доповнення, яке є P (F) = 1 - P (S) |
| Крок 3 | Використовуйте правило P (A або B), щоб знайти ймовірність певної послідовності певної послідовності успіхів і невдач, таких як SFFSSS, шляхом множення окремих ймовірностей. |
| Крок 4 | R визнати, що всі комбінації r успіхів з вибірки розміру n мають однакову ймовірність виникнення. Знайдіть кількість комбінацій nCr і помножте на цей раз ймовірність будь-якої з комбінацій, щоб визначити ймовірність отримання r успіхів з вибірки розміром n. |
Крок 5 - Як можна знайти точне p-значення за допомогою біноміального розподілу?
Нагадаємо, що в главі 2 ми визначили, яка гіпотеза була підкріплена знаходженням p-значення. Якщо p-значення було невеликим, меншим за рівень значущості, ми дійшли висновку, що дані підтримують альтернативну гіпотезу. Якщо p-значення було більше рівня значущості, ми зробили висновок, що дані підтримують нульову гіпотезу. Значення p - це ймовірність отримання даних, або більш екстремальних даних, припускаючи, що нульова гіпотеза вірна.
На кроці 4 ми знайшли ймовірність отримання даних (наприклад, чотири успіхи з 6), але ми ще не знайшли ймовірності отримання більш екстремальних даних. Для цього тепер ми повинні створити дистрибутиви. Розподіл показує ймовірність всіх можливих результатів експерименту. Для категоричних даних робимо дискретний розподіл.
Перш ніж розглядати розподіл, який має відношення до проблеми відповідальності за нещасні випадки, буде надано загальне обговорення розподілів.
У розділі 4 ви навчилися робити гістограми. Гістограми показують розподіл даних. У розділі 4 ви також дізналися про засоби і стандартні відхилення. Розподіли мають засоби і стандартні відхилення теж.
Щоб продемонструвати поняття, почнемо з простого прикладу. Припустимо, що у когось є два маршрути, які використовуються для бігу. Один маршрут довжиною 2 милі, а інший - 5 миль. Нижче наведено розклад роботи за минулий тиждень.
| Неділя | Понеділок | Вівторок | Середа | Четвер | П’ятниця | Субота |
| 5 | 2 | 2 | 5 | 2 | 2 | 5 |
Розподіл суми, що виконується щодня, наведено нижче.
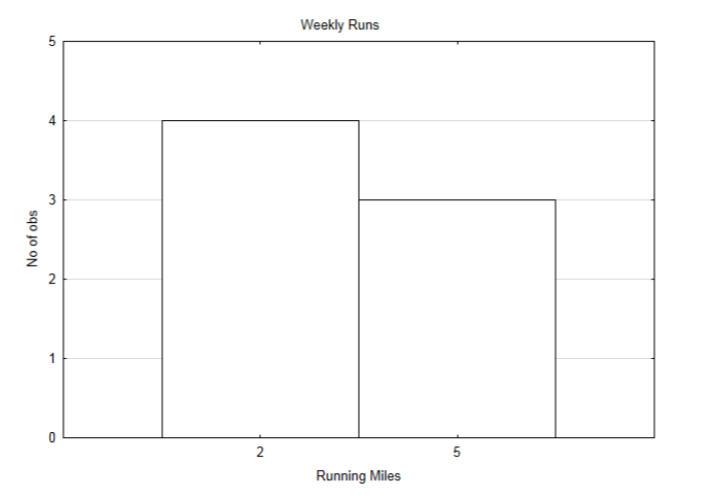
Середнє значення можна знайти, склавши всі щоденні пробіги і розділивши на 7. Середнє значення становить 3.286 миль на день. Оскільки однакові відстані повторюються в різні дні, також можна використовувати середнє зваження. У цьому випадку вага - це кількість разів, коли певна дистанція була пробігнута. Зважене середнє використовує переваги множення замість додавання. Таким чином, замість обчислення:\(\dfrac{2 + 2 + 2 + 2 + 5 + 5 + 5}{7} = 3.286\). ми можемо помножити кожне число на кількість разів, коли воно відбувається, потім розділити на кількість входжень:\(\dfrac{4 \cdot 2 + 3 \cdot 5}{4 + 3} = 3.286\). Формула середнього зваження така:
\[\dfrac{\sum w \cdot x}{\sum w}\]
Такий же графік представлений нижче, але на цей раз є відсотки над барами.
Замість того, щоб використовувати підрахунок як вага, відсотки (насправді пропорції) можуть бути використані як вага. Таким чином 57,143% можна записати як 0.57143. Так само 42.857% можна записати 0.42857.
Підстановка в формулу дає:\(\dfrac{0.57143 \cdot 2 + 0.42857 \cdot 5}{0.57143 + 0.42857} = 3.286\). Зверніть увагу, що знаменник додає до 1. Тому, якщо вага - це частка разів, що виникає значення, то середнє значення розподілу, яке використовує відсотки, можна знайти за формулою:
\[\mu = \sum P(x) x\]
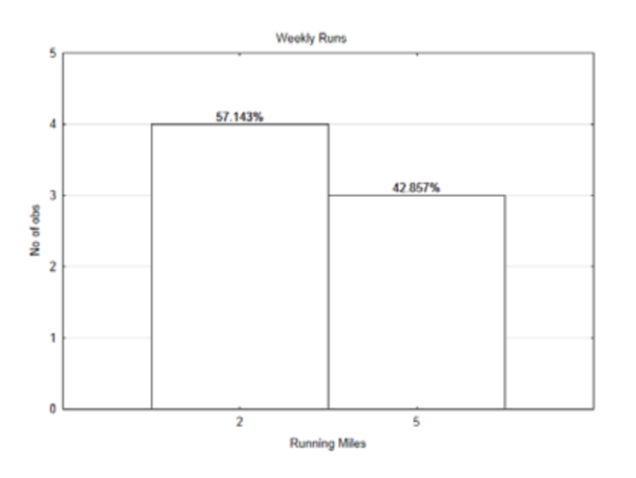
Це середнє значення, яке також відоме як очікуване значення, є сумою ймовірності значення, помноженої на значення. Немає необхідності в діленні, як це прийнято при знаходженні засобів, тому що ми завжди просто ділимо на 1.
Нагадаємо з глави 4, що стандартне відхилення - квадратний корінь дисперсії. Дисперсія є\(\sigma^2 = \sum[(x - \mu)^2 \cdot P(x)]\). Стандартне відхилення - це\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\).
\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\).
\(\sigma = \sqrt{(2 - 3.286)^2 \cdot 0.57143 + (5 - 3.286)^2 \cdot 0.42857} = 1.485\)
Проблема самостійного водіння автомобіля покаже нам один із способів, в якому ми стикаємося з дискретними розподілами. Насправді це призведе до створення особливого виду дискретного розподілу під назвою Біноміальний розподіл, який буде визначено після вивчення понять, що призводять до його створення.
При тестуванні гіпотези про пропорції успіхів є дві випадкові величини, які нас цікавлять. Перша випадкова величина специфічна для даних, які ми будемо збирати. Наприклад, у дослідженнях про те, хто несе відповідальність за аварії, спричинені автономними автомобілями, випадкова величина буде «відповідальною стороною». Було б два можливі значення для цієї випадкової величини, власника або виробника автомобіля. Ми вважаємо власника успішним, а виробника - невдачею. Дані, які збирають дослідники, стосуються цієї випадкової величини. Однак створення розподілів і знаходження ймовірностей і p-значень вимагає зсуву нашого фокусу на іншу випадкову величину. Ця друга випадкова величина - це кількість успіхів у вибірці розміру n Іншими словами, якщо запитують шість людей, скільки з них вважають, що власник несе відповідальність? Цілком можливо, що ніхто з них не вважає власником відповідальності, або хтось вважає, що власник несе відповідальність, або два, або три, або чотири, або п'ять, або всі шість думають, що власник несе відповідальність. Тому в вибірці розміром 6 випадкова величина числа успіхів може мати значення 0,1,2,3,4,5,6. Ми вже з'ясували, що ймовірність отримання чотирьох успіхів становить 0.3110. Тепер ми знайдемо ймовірність отримання 0,1,2,3,5,6 успіхів, припускаючи, що гіпотези все ще\(H_0: p = 0.60\) є\(H_1: p > 0.60\). Це дозволить створити дискретний біноміальний розподіл всіх можливих результатів.
Знайдіть ймовірність 0 успіхів
Єдиний спосіб досягти 0 успіхів - це мати всі невдачі, тому ми шукаємо P (FFFFFF).
Р (ФФФФФ) = Р (Ф) Р (Ф) Р (Ф) Р (Ф) Р (Ф) Р (Ф) = (0,4) (0,4) (0,4) (0,4) (0,4) (0,4) (0,4) (0,4) = 0,004096.
Так як існує тільки одна комбінація на 0 успіхів, то ймовірність 0 успіхів дорівнює 0,0041.
Знайти ймовірність 1 успіху
Ми знаємо, що всі комбінації мають однакову ймовірність, тому ми можемо створити найпростішу комбінацію для 1 успіху. Це був би SFFFFF.
П (СФФФФФ) = П (С) Р (Ф) Р (Ф) Р (Ф) Р (Ф) Р (Ф) = (0,6) (0,4) (0,4) (0,4) (0,4) (0,4) (0,4) =\((0.6)^{1}(0.4)^{5}\) = 0,006144.
Скільки комбінацій для 1 успіху? Це можна знайти за допомогою\(_6C_1\).
\(_6C_1 = \dfrac{6!}{(6 - 1)!1!} = 6\)комбінації. Чи здається ця відповідь розумною? Вважайте, що є лише 6 місць, в яких міг би статися успіх.
Імовірність 1 успіху тоді 6*0.006144 = 0,036864 або якщо округлити до чотирьох знаків після коми, 0,0369.
Знайдіть ймовірність 2 успіхів.
Замість того, щоб робити цю проблему поетапно, як це було зроблено для попередніх прикладів, вона буде продемонстрована шляхом комбінування кроків.
\(_6C_2 P\)(ПСФФФ)
\(\dfrac{6!}{(6 - 2)! 2!} (0.6)(0.6)(0.4)(0.4)(0.4)(0.4) = \dfrac{6!}{(6 - 2)! 2!} (0.6)^2(0.4)^4 =\)
15 (0,009216) = 0,1824 або з округленням до чотирьох знаків після коми 0,1382.
Знайдіть ймовірність 3 успіхів за допомогою комбінованих кроків. (Тепер ваша черга).
Знайдіть ймовірність 5 успіхів.
Знайдіть ймовірність 6 успіхів.
Коли всі ймовірності будуть знайдені, ми можемо створити таблицю, яка показує значення, які може приймати випадкова величина, і їх ймовірності. Визначимо випадкові величини для кількості успіхів як X з можливими значеннями, визначеними як x.
| Х = х | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Р (Х = х) | 0.0041 | 0.0369 | 0.1382 | 0,2765 | 0,3110 | 0.1866 | 0.0467 |
Чи згодні ваші значення для 3,5, і 6 успіхів зі значеннями, знайденими в таблиці?
Графік цього розподілу може призвести до кращого його розуміння. Цей графік називається імовірнісною масовою функцією, яка показана за допомогою графіка палиці. Це спосіб графіків дискретних розподілів, оскільки між числами на осі x не може бути жодних значень. Висоти планки відповідають ймовірності отримання кількості успіхів.
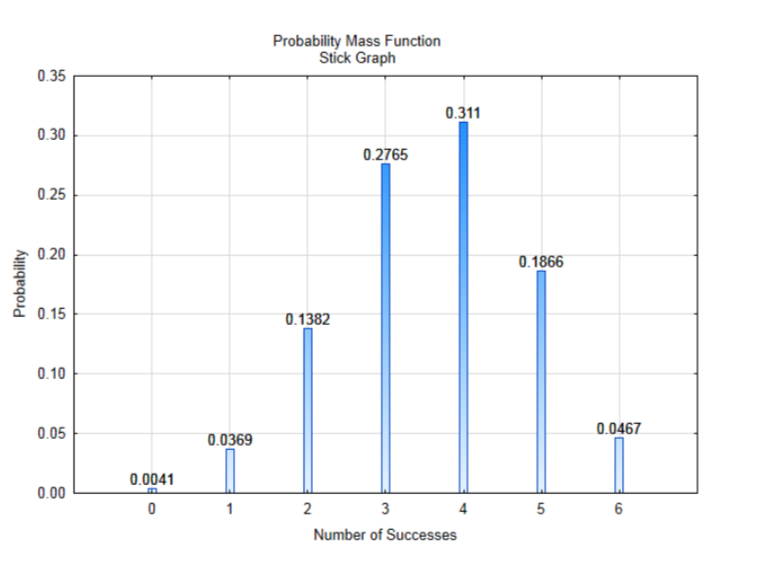
Є три речі, які ви повинні помітити про цей розподіл. По-перше, це повний розподіл. Тобто, у вибірці розміром шість можна мати лише 0,1,2,3,4,5 або 6 успіхів, і всі вони були включені до графіка. Друге, на що слід звернути увагу, це те, що всі ймовірності мають значення від 0 до 1. Цього слід очікувати, оскільки ймовірності завжди повинні бути між 0 та 1. Останнє, що слід помітити, що спочатку може бути не очевидним, полягає в тому, що якщо додати всі ймовірності, сума буде дорівнює 1. Сума всіх повних розподілів ймовірностей повинна дорівнювати 1,\(\sum P(x) =1\). Якщо ви додасте всі ймовірності, і вони не дорівнюють одній, але дуже близькі, це може бути через округлення, а не тому, що ви зробили щось неправильне.
Відступ 5 - Біноміальні розподіли
Весь шлях, який був здійснений з початку цієї глави, призвів до створення дуже важливого дискретного розподілу, який називається біноміальним розподілом, який має наступні компоненти.
- Пробний процес Бернуллі - це зразок, який може мати лише два можливі результати, успіх та невдачу.
- Експеримент може складатися з незалежних випробувань Бернуллі.
- Біноміальна випадкова величина, X - це кількість успіхів в експерименті
- Біноміальний розподіл показує всі значення для X і ймовірність виникнення кожного з цих значень.
Припущення такі, що:
- Всі випробування незалежні.
- Кількість випробувань в експерименті однакова і визначається змінною n.
- Імовірність успіху залишається постійною для кожного зразка. Імовірність невдачі є доповненням ймовірності успіху. Змінна p = P (S) і змінна\(q = P(F). q = 1 – p\).
- Випадкова величина X може мати значення 0, 1, 2,... n.
Імовірність можна знайти для кожного можливого числа успіхів, які випадкова величина X може мати за допомогою біноміальної формули розподілу.
\[P(X = x) = _nC_x P^x q^{n-x}\].
Якщо ця формула виглядає заплутаною, перегляньте роботу, яку ви зробили, знайшовши ймовірність того, що 3,5 або 6 людей вважають, що власник несе відповідальність, тому що ви насправді використовували цю формулу. \(_nC_x\), який показаний у вашому калькуляторі як\(_nC_r\), - це кількість комбінацій для x успіхів. X і r представляють одне і те ж і використовуються взаємозамінно.
р - ймовірність успіху. Вона походить від нульової гіпотези.
q - ймовірність виходу з ладу. Вона є доповненням р.
n - розмір вибірки
x - кількість успіхів
Якщо використовувати цю формулу для всіх можливих значень випадкової величини X, ми можемо створити біноміальний розподіл і графік.
\(P(X = 0) = _6C_0(0.60)^0(0.40)^{6 - 0} = 0.0041\)
\(P(X = 1) = _6C_1(0.60)^1(0.40)^{6 - 1} = 0.0369\)
\(P(X = 2) = _6C_2(0.60)^2(0.40)^{6 - 2} = 0.1382\)Можна закінчити і інші з них.
Калькулятор TI84 має простіший спосіб створити цей розподіл. Знайдіть і натисніть клавішу Y =. Курсор повинен з'явитися в пробілі поруч з Y1 =. Далі натискаємо\(2^{\text{nd}}\) ключ, потім ключ з VARS на ньому і DISR над ним. Це перенесе вас до колекції дистрибутивів. Прокрутіть вгору, поки не знайдете Binompdf. Це біноміальна функція розподілу ймовірностей. Виберіть його і введіть три значення n, p, x Наприклад, якщо ви введете Y1=Binompdf (6,0.60, x), а потім виберіть\(2^{\text{nd}}\) TABLE, ви побачите таблицю, яка виглядає наступним чином:
Х Я1
0 0,0041
1 0,03686
2 0,1824
3 0,27648
4 0,31104
5 0.18662
6 0,04666
Якщо таблиця не виглядає так, натисніть\(2^{\text{nd}}\) TBLSET і переконайтеся, що ваші налаштування:
TBlStart = 0
\(\Delta\) TBL =
1 Відступ:
Автозалежність: Авто.
Біноміальні розподіли мають середнє і стандартне відхилення. Підхід до знаходження середнього та стандартного відхилення дискретного розподілу може бути застосований до біноміального розподілу.
| \(X = x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(P(x = x)\) | 0.0041 | 0.0369 | 0.1382 | 0,2765 | 0,3110 | 0.1866 | 0.0467 |
| \(x(P(x))\) | 0 | 0.0369 | 0,2764 | 0,8295 | 1.244 | 0.933 | 0,2802 |
| \((x - \mu)^2\) | \((0 - 3.6)^2 = 12.96\) | 6.76 | 2.56 | 0,36 | 0,16 | 1.96 | 5.76 |
| \((x - \mu)^2 \cdot P(x)\) | 0.0531 | 0,2494 | 0,3538 | 0.0995 | 0.0498 | 0,3657 | 0,2690 |
\(\mu = \sum P(x) x\)
\(\mu = 0 + 0.0369+0.2764+0.8295+1.244+0.933+0.2802 = 3.6\)
\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\)
\(\sigma = \sqrt{0.0531 + 0.2494 + 0.3538 + 0.0995 + 0.0498 + 0.3657 + 0.2690} = \sqrt{1.4403} = 1.20\)
Середнє значення ще називають очікуваним значенням розподілу. Пошук очікуваного значення та стандартного відхилення для використання цих формул може бути дуже нудним. На щастя, для біноміального розподілу існує більш простий спосіб. Очікуване значення можна знайти за формулою:
\[E(x) = \mu = np\]
Стандартне відхилення знаходять за формулою
\[\sigma = \sqrt{npq} = \sqrt{np(1 - p)}\]
Щоб визначити середню кількість людей, які вважають, що власник несе відповідальність за нещасні випадки, скористайтеся формулою
\(E(x) = \mu = np = 6\ (0.6) = 3.6\).
Це вказує на те, що якби було взято багато зразків з 6 людей, середня кількість людей, які вважають, що власник несе відповідальність, становила б 3,6. Прийнятно, щоб це середнє значення не було цілим числом.
Стандартне відхилення цього розподілу становить:\(\sigma = \sqrt{np(1 - p)} = \sqrt{6 (0.6) (0.4)} = 1.2\)
Зверніть увагу, що ті ж результати були отримані з більш легким процесом. Формули 5.12 і 5.13 слід використовувати для пошуку середнього та стандартного відхилення для всіх біноміальних розподілів.
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Тепер, коли у вас є можливість створити повний біноміальний розподіл, ви готові перевірити гіпотезу. Це буде продемонстровано на прикладі автономного автомобіля, який використовувався протягом усього цього розділу.
Припустимо, дослідник хотів визначити частку людей, які вважають, що власник несе відповідальність. Дослідник, можливо, мав гіпотезу, що частка людей, які вважають, що власник несе відповідальність за нещасні випадки, становить понад 60%. В цьому випадку гіпотези будуть такими: Н0: р = 0,60 і Н1: р > 0,60. Рівень значущості становитиме 0,10, оскільки буде використовуватися лише невеликий розмір вибірки. В цьому випадку розмір вибірки буде дорівнює 6.
З цим розміром вибірки ми вже бачили, яким буде біноміальний розподіл. Ми також знаємо, що напрямок крайності праворуч, оскільки альтернативна гіпотеза використовує більше, ніж символ.
Дослідник випадковим чином вибирає 6 осіб. З них четверо кажуть, що власник несе відповідальність. Яку гіпотезу підтверджують ці дані?
Значення p - це ймовірність того, що дослідник отримає чотири або більше людей, які стверджують, що власник несе відповідальність. З таблиці, яку ми створили раніше, бачимо ймовірність отримати 4 людини, які думають
| \(X = x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(P(X = x)\) | 0.0041 | 0.0369 | 0.1382 | 0,2765 | 0,3110 | 0.1866 | 0.0467 |
власник несе відповідальність 0,3110, ймовірність отримання 5 - 0,1866 і ймовірність отримання 6 - 0,0467. Якщо скласти їх разом, ми виявимо ймовірність отримання 4 або більше дорівнює 0.5443. Оскільки ця ймовірність більша за наш рівень значущості, ми робимо висновок, що дані підтримують нульову гіпотезу і тому не є суттєвими. Висновок, який був би написаний: На рівні 0,10 значущості частка людей, які вважають, що власник несе відповідальність, не значно перевищує 0,60 (\(x = 4\),\(p = 0.5443\),\(n = 6\)). Пам'ятайте, що в статистичних висновках p - це p-значення, а не пропорція вибірки.
TI84 має швидкий спосіб скласти ймовірності. Він використовує функцію binomcdf, для біноміальної функції кумулятивного розподілу. Він знаходиться в списку\(2^{\text{nd}}\) дистрибутивів DISTR. Binomcdf складатиме всі ймовірності, що починаються зліва, таким чином binomcdf (6, .6,1) додасть ймовірності для 0 та 1. Існує дві умови, які зустрічаються при перевірці гіпотез з використанням біноміального розподілу. Спосіб знаходження p-значення за допомогою binomcdf заснований на альтернативній гіпотезі.
Умова 1. Альтернативна гіпотеза має знак менше (<).
Так як напрямок крайності - вліво, то за допомогою binomcdf (n, p, x) буде отримано значення p. Змінна n представляє розмір вибірки, змінна p представляє ймовірність успіху (див. Нульова гіпотеза), а x представляє конкретну кількість успіхів з даних.
Стан 2. Альтернативна гіпотеза має знак більше (>).
Оскільки напрямок крайності вправо, необхідно використовувати правило доповнення, а також зменшити значення\(x\) на 1, тому введіть 1 — binomcdf (\(n\)\(p\),\(x - 1\)) у вашому калькуляторі. Наприклад, якщо даних 4, то введіть 1 — binomcdf (6,0.6,3). Чи можете ви зрозуміти, чому використовується x — 1 і чому binomcdf (n, p, x-1) віднімається від 1? Якщо ні, запитайте на уроці.
У цьому прикладі дані не були значними, і тому дослідник не міг стверджувати, що частка людей, які вважають, що власник несе відповідальність більше 0,60. Розмір вибірки 6 дуже малий для категоричних даних, і тому важко досягти будь-яких значних результатів. Якщо дані змінені так, що замість того, щоб отримати 4 з 6 осіб, дослідник отримує 400 з 600, чи змінюється висновок? Використовуйте 1 — binomcdf (600,0,6,399), щоб знайти p-значення для цієї ситуації.
1 — біномдф (600,0,6,399) = ____________________
Напишіть заключне речення:
Крок 6 - Як знайти приблизне p-значення за допомогою нормального наближення до біноміального розподілу?
При перевірці гіпотези з використанням біноміального розподілу виявляється точне p-значення. Саме тому, що біноміальний розподіл створюється з кожної комбінації успіхів і невдач, яка можлива для вибірки розміру n, Існують і інші методи визначення p-значення, які дадуть приблизне p-значення. Насправді типовий метод, який використовується для перевірки гіпотез про пропорції, дасть приблизне p-значення. Ви можете задатися питанням, чому замість методу, який дає точне p-значення, використовується метод, який дає точне p-значення. Це буде пояснено після того, як будуть продемонстровані наступні два методи. Перш ніж їх можна буде продемонструвати, нам потрібно дізнатися про інший розподіл, який називається нормальним розподілом.
Відступ 6 - Нормальний розподіл
За коледжем Пірса знаходиться озеро Уогхоп, яке використовується багатьма студентами для вивчення наукових концепцій поза класом. Приблизна форма озера показана нижче. Якщо одна з наукових лабораторій вимагала від студентів оцінити площу поверхні води, яку стратегію вони могли б використовувати для цього озера неправильної форми?
Можлива стратегія полягає в тому, щоб думати, що це озеро майже прямокутник, і щоб вони могли намалювати прямокутник над ним. Оскільки формула відома для площі прямокутника, і якщо ми знаємо, що кожна стрілка нижче становить 200 метрів, чи можна оцінити площу озера?
Є два важливих питання, які слід розглянути. Якщо такий підхід буде прийнятий, чи буде площа озера в точності дорівнює площі прямокутника? Чи буде це близько?
Відповідь на перше питання - ні, якщо тільки нам не довелося вкрай пощастило з нашим малюнком прямокутника. Відповідь на друге питання - так, він повинен бути близьким. 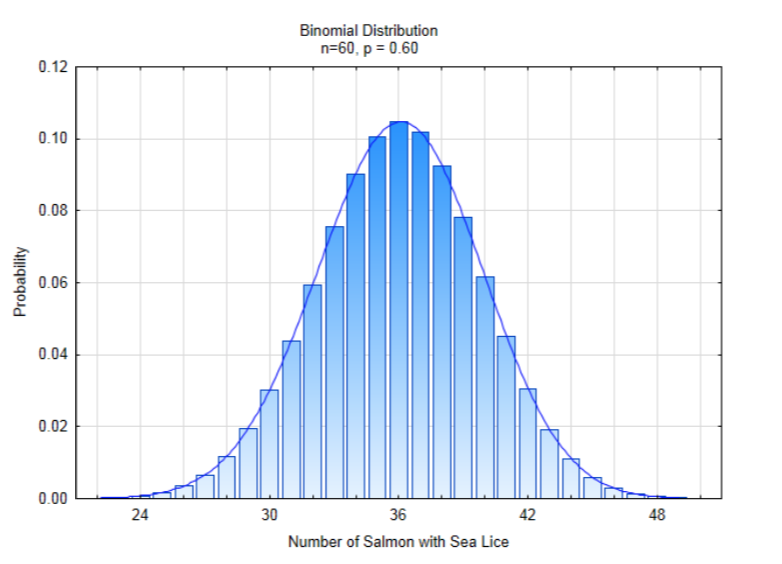
Концепція наближення неправильної форми формою, для якої відомі властивості, - це стратегія, яку ми будемо використовувати для пошуку нових способів визначення p-значення. Праворуч - неправильна форма біноміального розподілу, якщо n = 60, p = 0,60. Плавна крива, яка намальована над вершиною брусків, називається нормальним розподілом. Він також йде за назвами кривої дзвінка і гауссового розподілу.
Формула нормального розподілу є\(f(x, \mu, \sigma) = \dfrac{1}{\sigma \sqrt{2\pi}} e^{[\dfrac{1}{2} (\dfrac{x - \mu}{\sigma})^2]}\). Не важливо, щоб ви знали цю формулу. Що важливо - помітити в ньому змінні. Обидва πі e є константами зі значеннями 3,14159 і 2,71828 відповідно. x - незалежна змінна, яка знаходиться вздовж осі x. Важливими змінними, які слід помітити, є μ і σ, середнє і стандартне відхилення. Наслідком цих двох змінних є те, що вони відіграють важливу роль у визначенні цієї кривої. Функція може бути показана як\(N(\mu,\sigma)\).
Біноміальний розподіл є дискретним розподілом, тоді як нормальний розподіл є безперервним розподілом. Він відомий як функція щільності.
Нормальний розподіл контрастується з перекосованими розподілами нижче.
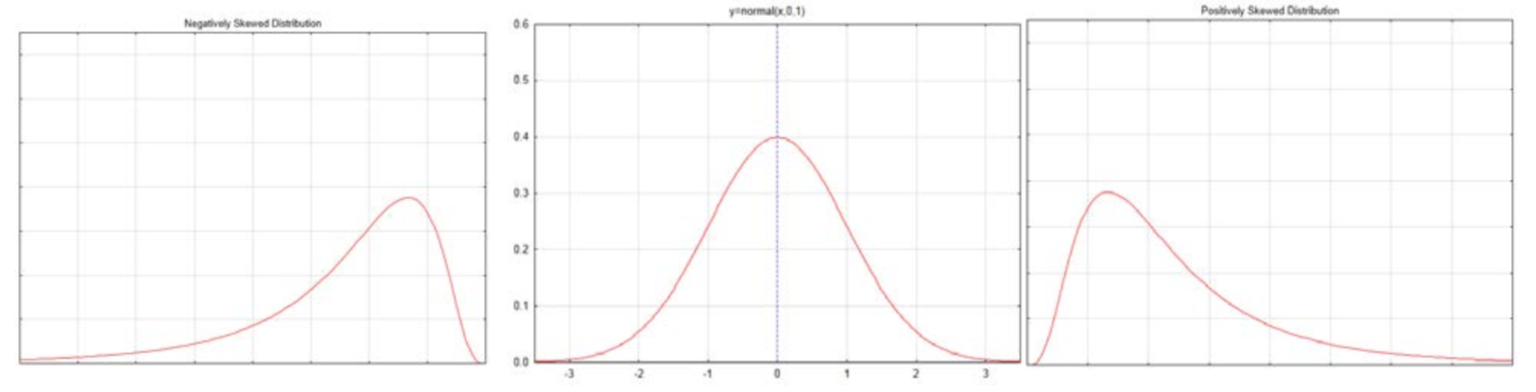
Негативно перекошений розподіл, наприклад, показано ліворуч, має деякі значення, які дуже низькі, що призводить до розтягування кривої вліво. Ці низькі значення призведуть до того, що середнє значення буде меншим за медіану для розподілу. Позитивно перекошений розподіл, наприклад, показано праворуч, має деякі значення, які дуже високі, внаслідок чого крива розтягується вправо. Ці високі значення призведуть до того, що середнє значення буде більшим за медіану для розподілу. Нормальна крива посередині симетрична. Середнє, медіана і режим знаходяться в середині. Режим - це найвища точка кривої.
Нормальна крива називається функцією щільності, на відміну від біноміального розподілу, який є імовірнісної масовою функцією. Простір під кривою називається площею під кривою. Площа є синонімом ймовірності. Площа під всією кривою, відповідна ймовірності вибору значення з будь-якої точки розподілу, дорівнює 1. Ця крива ніколи не стосується осі х, незважаючи на те, що вона виглядає так, як це робить. Наша кінцева мета з кривою nor mal - знайти площу в хвості, що відповідає знаходженню p-значення.
mal - знайти площу в хвості, що відповідає знаходженню p-значення.
Ми почнемо думати про площу (ймовірність) під кривою, подивившись на стандартну нормальну криву. Стандартна нормальна крива має середнє значення 0 і стандартне відхилення 1 і показана у вигляді функції N (0,1). Зверніть увагу, що вісь x кривої нумерується —3, -2, -1, 0, 1, 2, 3. Ці числа називаються z scores. Вони являють собою число стандартних відхилень х є від середнього, яке знаходиться в середині кривої.
Чи здається розумним, що половина кривої знаходиться зліва від середнього, а половина кривої - праворуч? Ми можемо позначити кожну сторону цим значенням, яке інтерпретується як область і ймовірність того, що значення буде існувати в цій області. 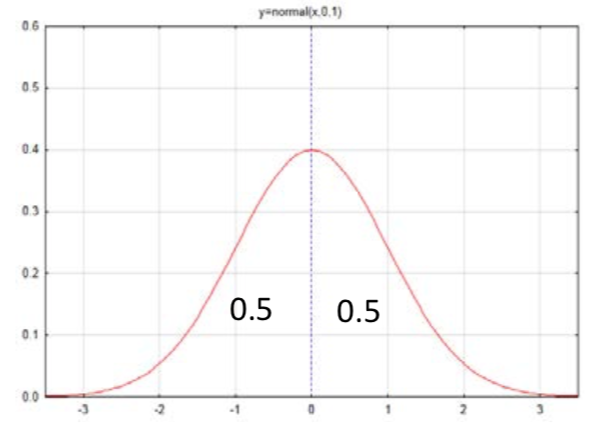
Думати про площу при нормальному розподілі не так просто, як думати про площу під рівномірним розподілом. Наприклад, ми могли б створити рівномірний розподіл для результату експерименту, в якому згортається одна матриця. Імовірність прокатки будь-якого числа дорівнює 1/6. Тому рівномірний розподіл виглядав би так.
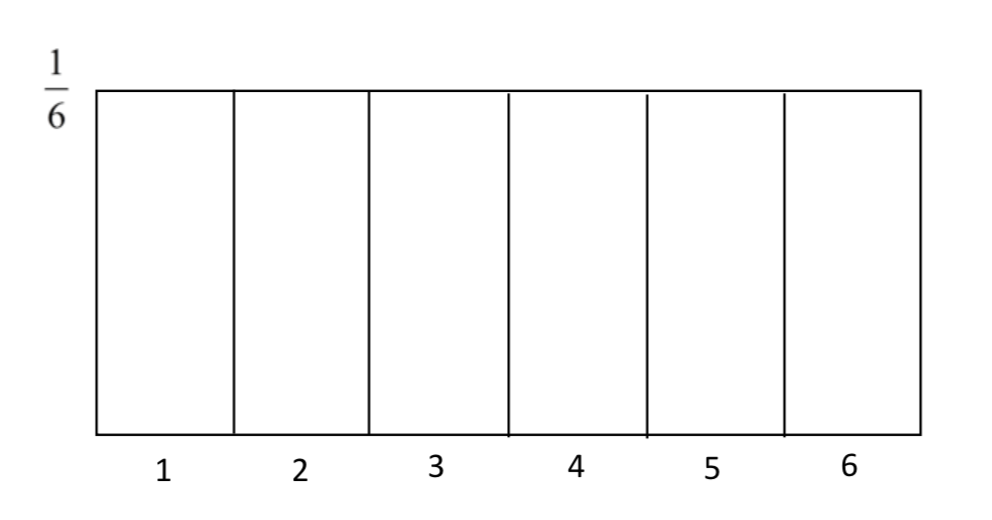
Площа на цьому розподілі можна знайти, помноживши довжину на ширину (висоту). Таким чином, щоб знайти ймовірність отримання 5 або вище, вважаємо довжину рівною 2, а ширину - 1/6 так\(2 \times (\dfrac{1}{6} = \dfrac{1}{3}\). Тобто існує ймовірність 1/3, що 5 або 6 будуть кататися на матриці.
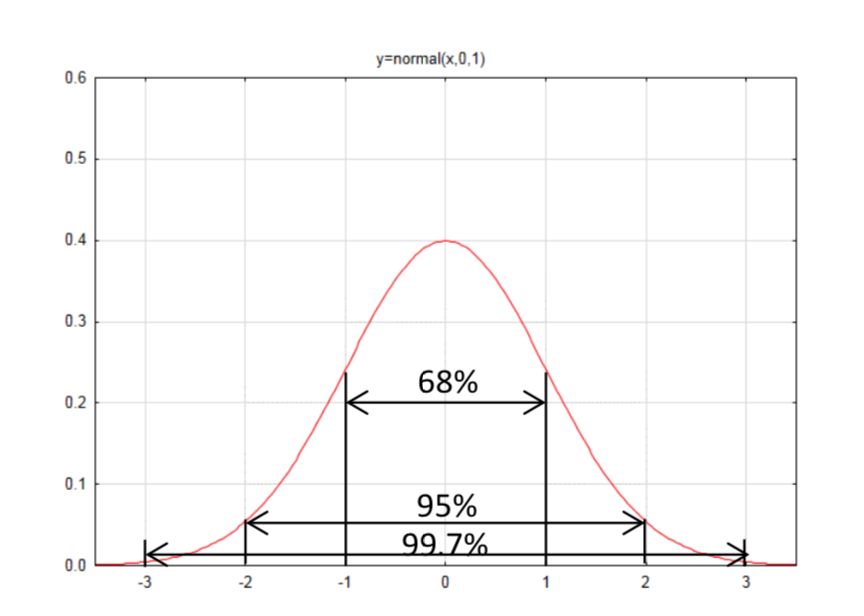
Але нормальний розподіл не так звичний, як прямокутник, для якого область знайти простіше. Емпіричне правило - це наближення площ для різних ділянок нормальної кривої; 68% кривої знаходиться в межах одного стандартного відхилення від середнього, 95% кривої знаходиться в межах двох стандартних відхилень від середнього, а 99,7% кривої знаходиться в межах трьох стандартних відхилень від середнього.
Знайти область під нормальним розподілом спочатку було зроблено за допомогою методики, яка називається інтеграцією, яка викладається в Обчислення. Однак ці області вже знайдені для стандартного нормального розподілу N (0,1) і наведені в таблиці на наступній сторінці. У таблицях завжди буде вказана область зліва. Область праворуч є доповненням області зліва, тому, щоб знайти область праворуч, відніміть область зліва від 1. Кілька прикладів повинні допомогти прояснити це.
Приклад 3. Знайдіть області ліворуч і праворуч від z = -1.96.
Оскільки значення z менше 0, використовуйте першу з двох таблиць. Знайдіть рядок з - 1.9 у лівому стовпчику та знайдіть стовпчик з 0.06 у верхньому рядку. Перетин цих рядків і стовпців дає область зліва, позначену\(A_L\) як 0,0250. Область праворуч, позначена як\(A_R = 1 – 0.0250 = 0.9750\).
| Z | 0,09 | 0,08 | 0,07 | 0,06 | 0,05 | 0,04 | 0,03 | 0,02 | 0,01 | 0.00 |
| -1.9 | 0.0233 | 0.0239 | 0.0244 | 0.0250 | 0.0256 | 0.0262 | 0.0268 | 0.0274 | 0.0281 | 0.0287 |
Приклад 4. Знайдіть області ліворуч і праворуч від z = 0,57.
Оскільки значення z більше 0, використовуйте другу з двох таблиць. Знайдіть рядок з 0.5 в лівій колонці і знайдіть стовпець з 0.07 у верхньому рядку. Отже, перетин цих рядків і\(A_L = 0.7157\) стовпців дає\(A_R = 1 – 0.7157 = 0.2843\).
Стандартний нормальний розподіл — N (0,1)
Площа ліворуч, коли\(z \le 0\)
| Z | 0,09 | 0,08 | 0,07 | 0,06 | 0,05 | 0,04 | 0,03 | 0,02 | 0,01 | 0.00 |
| -3.5 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| -3.4 | 0.0002 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 |
| -3.3 | 0.0003 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0005 | 0,0005 | 0,0005 |
| -3.2 | 0,0005 | 0,0005 | 0,0005 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0007 | 0.0007 |
| -3.1 | 0.0007 | 0.0007 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 0.0009 | 0.0009 | 0.0009 | 0,0010 |
| -3.0 | 0,0010 | 0,0010 | 0,0011 | 0,0011 | 0,0011 | 0,0012 | 0,0012 | 0,0013 | 0,0013 | 0,0013 |
| -2.9 | 0,0014 | 0,0014 | 0,0015 | 0,0015 | 0,0016 | 0,0016 | 0,0017 | 0,0018 | 0,0018 | 0,0019 |
| -2.8 | 0,0019 | 0,0020 | 0,0021 | 0,0021 | 0,0022 | 0,0023 | 0,0023 | 0,0024 | 0,0025 | 0,0026 |
| -2.7 | 0,0026 | 0,0027 | 0,0028 | 0,0029 | 0,0030 | 0,0031 | 0,0032 | 0,0033 | 0,0034 | 0,0035 |
| -2.6 | 0,0036 | 0,0037 | 0,0038 | 0,0039 | 0,0040 | 0.0041 | 0.0043 | 0,0044 | 0,0045 | 0,0047 |
| -2.5 | 0,0048 | 0,0049 | 0,0051 | 0,0052 | 0,0054 | 0,0055 | 0,0057 | 0.0059 | 0,0060 | 0,0062 |
| -2.4 | 0,0064 | 0.0066 | 0.0068 | 0,0069 | 0,0071 | 0.0073 | 0,0075 | 0,0078 | 0,0080 | 0,0082 |
| -2.3 | 0,0084 | 0,0087 | 0,0089 | 0,0091 | 0,0094 | 0,0096 | 0,0099 | 0.0102 | 0.0104 | 0.0107 |
| -2.2 | 0.0110 | 0.0113 | 0.0116 | 0.0119 | 0.0122 | 0.0125 | 0.0129 | 0.0132 | 0.0136 | 0.0139 |
| -2.1 | 0.0143 | 0.0146 | 0,0150 | 0.0154 | 0.0158 | 0.0162 | 0.0166 | 0.0170 | 0.0174 | 0.0179 |
| -2.0 | 0.0183 | 0.0188 | 0.0192 | 0.0197 | 0.0202 | 0.0207 | 0.0212 | 0.0217 | 0.0222 | 0.0228 |
| -1.9 | 0.0233 | 0.0239 | 0.0244 | 0.0250 | 0.0256 | 0.0262 | 0.0268 | 0.0274 | 0.0281 | 0.0287 |
| -1.8 | 0.0294 | 0.0301 | 0.0307 | 0.0314 | 0.0322 | 0.0329 | 0.0336 | 0.0344 | 0.0351 | 0.0359 |
| -1.7 | 0.0367 | 0.0375 | 0.0384 | 0.0392 | 0.0401 | 0.0409 | 0.0418 | 0.0427 | 0.0436 | 0.0446 |
| -1.6 | 0.0455 | 0.0465 | 0.0475 | 0.0485 | 0.0495 | 0.0505 | 0.0516 | 0.0526 | 0.0537 | 0.0446 |
| -1.5 | 0.0559 | 0.0571 | 0.0582 | 0.0594 | 0.0606 | 0.0618 | 0.0630 | 0.0643 | 0.0655 | 0.0668 |
| -1.4 | 0.0681 | 0.0694 | 0.0708 | 0.0721 | 0.0735 | 0.0749 | 0.0764 | 0.0778 | 0.0793 | 0.0808 |
| -1.3 | 0.0823 | 0.0838 | 0.0853 | 0.0869 | 0.0885 | 0.0901 | 0.0918 | 0.0934 | 0.0951 | 0.0968 |
| -1.2 | 0.0985 | 0.1003 | 0,1020 | 0,1038 | 0,1056 | 0,1075 | 0,1093 | 0.1112 | 0.1131 | 0.1151 |
| -1.1 | 0,1170 | 0,1190 | 0.1210 | 0.1230 | 0,1251 | 0,1271 | 0,1292 | 0,1314 | 0,1334 | 0,1357 |
| -1.0 | 0.1379 | 0.1401 | 0,1423 | 0,1446 | 0,1469 | 0.1492 | 0,1515 | 0,1539 | 0,1562 | 0.1587 |
| -0.9 | 0.1611 | 0,1635 | 0,1660 | 0,1685 | 0.1711 | 0,1736 | 0,1762 | 0.1788 | 0,1814 | 0,1841 |
| -0.8 | 0,1867 | 0,1894 | 0,1922 | 0.1949 | 0,1977 | 0.2005 | 0,2033 | 0,2061 | 0,2090 | 0,2119 |
| -0.7 | 0,2148 | 0,2177 | 0,2206 | 0,2236 | 0,2266 | 0,2296 | 0,2327 | 0,2358 | 0,2389 | 0,2420 |
| -0.6 | 0,2451 | 0,2483 | 0,2514 | 0,2546 | 0,2578 | 0,2611 | 0,2643 | 0,2676 | 0,2709 | 0,2743 |
| -0.5 | 0,2776 | 0,2810 | 0,2843 | 0,2877 | 0,2912 | 0,2946 | 0,2981 | 0,3015 | 0,3050 | 0,3085 |
| -0.4 | 0,3121 | 0,3156 | 0,3192 | 0,3228 | 0,3264 | 0,3300 | 0,3336 | 0,3372 | 0,3409 | 0,3446 |
| -0.3 | 0,3483 | 0,3520 | 0,2557 | 0,3594 | 0,3632 | 0,3669 | 0,3707 | 0,3745 | 0,3783 | 0,3821 |
| -0.2 | 0,4247 | 0,4286 | 0,4325 | 0,4364 | 0,4404 | 0,4443 | 0,4483 | 0,4522 | 0,4562 | 0.4602 |
| 0.0 | 0,4641 | 0,4681 | 0,4721 | 0,4761 | 0.4801 | 0,4840 | 0,4880 | 0,4920 | 0,4960 | 0.5000 |
Стандартний нормальний розподіл — N (0,1)
Площа ліворуч, коли\(z \ge 0\)
| Z | 0.00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0.0 | 0.5000 | 0,5040 | 0,5080 | 0.5120 | 0,5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0,5359 |
| 0.1 | 0.5398 | 0,5438 | 0.5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0,5910 | 0.5948 | 0.5987 | 0.6026 | 0,6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0,6480 | 0,6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0,7019 | 0,7054 | 0.7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 |
| 0.6 | 0,7257 | 0,7291 | 0.7324 | 0,7357 | 0,7389 | 0.7422 | 0,7454 | 0,7486 | 0,7517 | 0,7549 |
| 0.7 | 0,7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0,7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0,8159 | 0.8186 | 0.8212 | 0.8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0.8365 | 0,8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0,8485 | 0,8508 | 0.8531 | 0,8554 | 0,8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0,9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0,9115 | 0.9131 | 0.9147 | 0,9162 | 0,9177 |
| 1.4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 |
| 1.5 | 0.9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0.9406 | 0,9418 | 0,9429 | 0,9441 |
| 1.6 | 0,9452 | 0,9463 | 0,9474 | 0,9484 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 |
| 1.7 | 0,9554 | 0,9564 | 0,9573 | 0.9582 | 0,9591 | 0,9599 | 0,9608 | 0.9616 | 0,9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0.9699 | 0.9706 |
| 1.9 | 0,9713 | 0,9719 | 0.9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9761 | 0,9767 |
| 2.0 | 0,9772 | 0,9778 | 0,9783 | 0,9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0,9817 |
| 2.1 | 0,9821 | 0.9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0.9846 | 0,9850 | 0,9854 | 0,9857 |
| 2.2 | 0,9861 | 0,9864 | 0.9868 | 0,9871 | 0,9875 | 0.9878 | 0.9881 | 0.9884 | 0,9887 | 0,9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0,991 | 0,9913 | 0,9916 |
| 2.4 | 0,9918 | 0,9920 | 0,992 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 |
| 2.5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 |
| 2.6 | 0,9953 | 0,955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 |
| 2.7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 |
| 2.8 | 0,9974 | 0,9975 | 0.9976 | 0,9977 | 0,9977 | 0,9978 | 0.9979 | 0.9979 | 0,9980 | 0,9981 |
| 2.9 | 0,9981 | 0,9982 | 0,9982 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 |
| 3.0 | 0,9987 | 0,9987 | 0,9987 | 0,9988 | 0,9988 | 0,9989 | 0,9989 | 0,9989 | 0,9990 | 0,9990 |
| 3.1 | 0,9990 | 0,9991 | 0,9991 | 0,9991 | 0,9992 | 0,9992 | 0,9992 | 0,9992 | 0,9993 | 0,9993 |
| 3.2 | 0,9993 | 0,9993 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9995 | 0,9995 | 0,9995 |
| 3.3 | 0,9995 | 0,9995 | 0. 995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0,9997 |
| 3.4 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0.9998 |
Оскільки дуже малоймовірно, що ми зіткнемося з автентичними популяціями, які зазвичай розподіляються із середнім нулем і стандартним відхиленням одиниці, то від чого це користь? Відповідь на це питання має дві частини. Перша частина - відповісти на питання про те, які корисні популяції зазвичай розподілені. Друга частина полягає у визначенні того, як ці таблиці можуть використовуватися іншими розподілами з різними засобами і стандартними відхиленнями.
Ви вже бачили, що нормальна крива дуже добре підходить до біноміального розподілу. У першому та другому розділах ви також бачили розподіли пропорцій зразків та засобів зразка, які виглядають нормально розподіленими. Тому основне використання нормального розподілу полягає у пошуку ймовірностей, коли він використовується для моделювання інших розподілів, таких як біноміальний розподіл або розподіли вибірки\(\hat{p}\) або\(\bar{x}\). Нижче ілюструють елементи розподілів, що моделюються кривою.
Тепер, коли деякі розподіли, які можна змоделювати за допомогою нормальної кривої, були встановлені, ми можемо вирішити друге питання, яке полягає в тому, як використовувати таблиці для стандартної нормальної кривої. Ймовірності та більш конкретно p-значення, можна знайти лише після того, як ми отримаємо результати вибірки. Ці вибіркові результати є частиною розподілу можливих результатів, які приблизно нормально розподіляються. Визначаючи кількість стандартних відхилень, які наші вибіркові результати складають від середнього значення популяції, ми можемо скористатися стандартними таблицями нормального розподілу, щоб знайти p-значення. При перетворенні результатів вибірки в стандартні відхилення від середнього використовується формула z.
Оцінка z - це кількість стандартних відхилень значення від середнього. Віднімаючи значення від середнього і діливши на стандартне відхилення, обчислюємо кількість стандартних відхилень. Формула така
\[z = \dfrac{x - \mu}{\sigma}\]
Це основна формула, на якій будуть побудовані багато інших.
Приклад 5
Припустимо, середнє число успіхів у вибірці 100 дорівнює 20, а стандартне відхилення - 4. Намалюйте і позначте нормальну криву і знайдіть область в лівому хвості для числа 13. 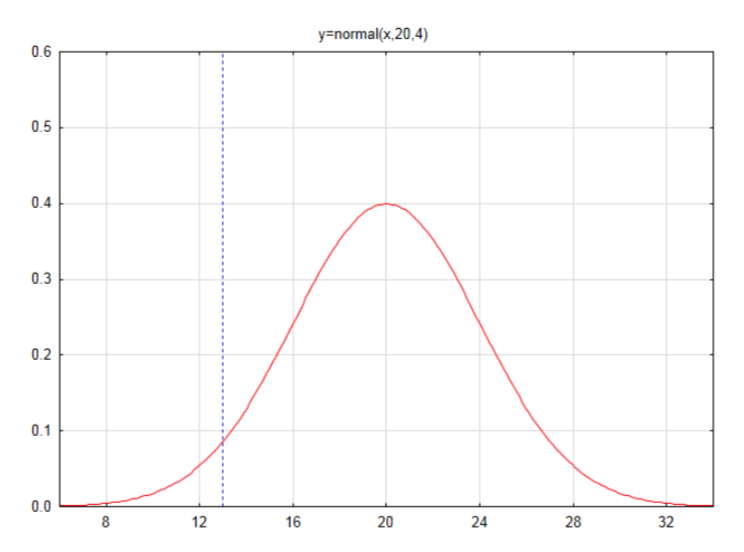
Спочатку знайдіть оцінку z:\(z = \dfrac{x - \mu}{\sigma}\)
\(z = \dfrac{13 - 20}{4} = -1.75\)
Знайдіть область зліва в таблиці
\(A_L = 0.0401\)
Приклад 6
Якщо середнє значення дорівнює 30, а стандартне відхилення дорівнює 5, то намалюйте і позначте нормальну криву і знайдіть область в правому хвості для числа 44.1.
Спочатку знайдіть оцінку z:\(z = \dfrac{x - \mu}{\sigma}\)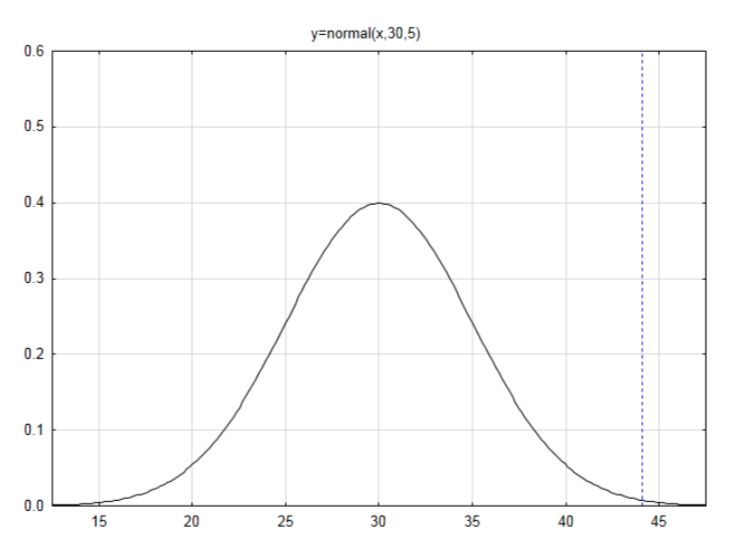
\(z = \dfrac{44.1 - 30}{5} = 2.82\)
Знайдіть область зліва в таблиці
\(A_L = 0.9976\)
Скористайтеся цим, щоб знайти область праворуч, віднімаючи від 1.
\(A_R = 0.0024\)
Повернення до кроку 6: Застосуйте це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Пам'ятайте, що гіпотезами щодо проблеми автономного автомобіля є:\(H_0: p = 0.60\),\(H_1: p > 0.60\). У первісній проблемі дослідник виявив, що 4 з 6 людей вважали, що власник несе відповідальність. Яку гіпотезу підтверджують ці дані, якщо рівень значущості дорівнює 0,10?
Цей тест гіпотези буде проведений за допомогою методу, який називається Нормальне наближення до біноміального розподілу.
Насамперед необхідно знайти середнє і стандартне відхилення біноміального розподілу (яке було зроблено раніше, але зараз повторюється):
\(\mu = np = 6(0.6) = 3.6\)
\(\sigma = \sqrt{npq} = \sqrt{6(0.6)(0.4)} = 1.2\)
Намалюйте і позначте нормальну криву із середнім значенням 3,6 і стандартним відхиленням 1,2.
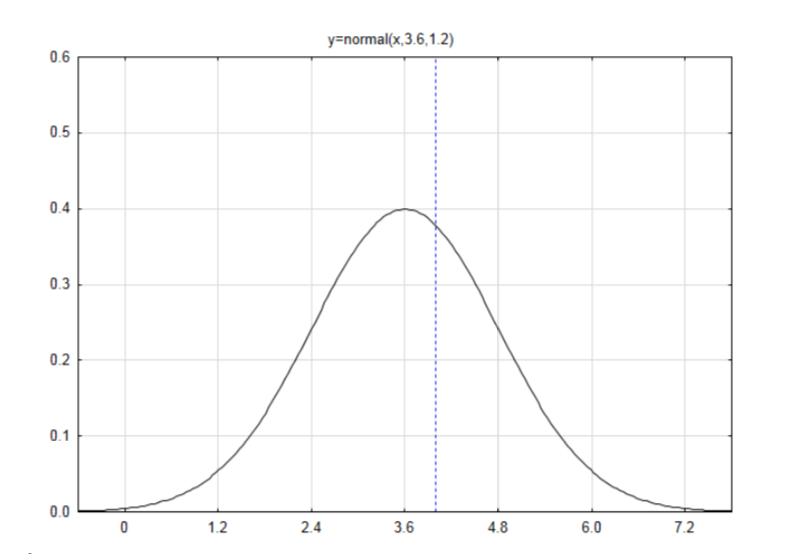
Знайдіть оцінку z, якщо дані 4.
\(z = \dfrac{x - \mu}{\sigma}\)\(z = \dfrac{4 - 3.6}{1.2} = 0.33\)
Від таблиці знаходиться область зліва\(A_L = 0.6255\). Оскільки напрямок крайнього - вправо, відніміть площу вліво від 1, щоб отримати\(A_R = 0.3745\). Це p-значення.
Це p-значення також можна знайти за допомогою калькулятора (\(2^{\text{nd}}\)Distr #2: normalcdf (низький, високий\(\mu\),\(\sigma\))), показаний як normalcdf (4, 1E99, 3.6,1.2) =0.3694.
Так як це значення більше рівня значущості, якщо використовується згенероване калькулятором p-значення, то висновок буде записаний так: При рівні значущості 0,10 частка людей, які вважають, що власник несе відповідальність, не значно більше 0,60 (z = 0,33, p = 0,3694, n = 6).
Тепер візьмемо момент, щоб порівняти p-значення від нормального наближення до біноміального розподілу (0,3694) до точного p-значення, знайденого за допомогою біноміального розподілу (0,5443). Хоча ці p- значення не дуже близькі один до одного, висновок, який робиться, однаковий. Причина, по якій вони не дуже близькі, полягає в тому, що розмір вибірки 6 дуже малий, а нормальне наближення не дуже добре при невеликому розмірі вибірки.
Перевірте гіпотезу ще раз, якщо дослідник виявить, що 400 з 600 людей вважають, що власник несе відповідальність за нещасні випадки.
\(\mu = np = 600(0.6) = 360\)Це вказує на те, що якби було відібрано багато зразків з 600 людей, середня кількість людей, які вважають, що власник несе відповідальність, становила б 360.
\(\sigma = \sqrt{npq} = \sqrt{600(0.6)(0.4)} = 12\)
Намалюйте мітку кривою із середнім значенням 360 і стандартним відхиленням 12.
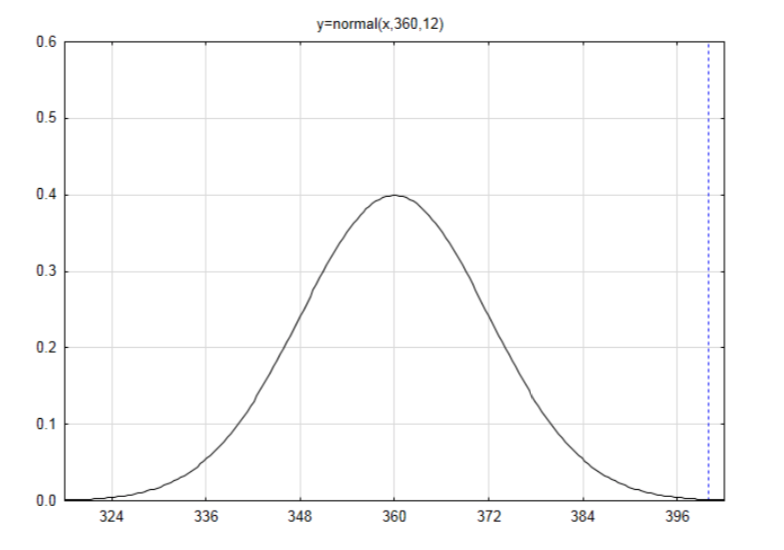
Знайдіть оцінку z, якщо дані дорівнюють 400.
\(z = \dfrac{x - \mu}{\sigma}\)\(z = \dfrac{400 - 360}{12} = 3.33\)
Використовуючи таблицю, область зліва знаходиться\(A_L = 0.9996\). Оскільки напрямок крайнього - вправо, відніміть площу вліво від 1, щоб отримати\(A_R = 0.0004\). Точніше, це 0.000430.
Цього разу, коли результати нормального наближення до біноміального розподілу (0.000430) порівнюються з результатами біноміального розподілу (0.000443), вони дуже близькі. Це пов'язано з тим, що розмір вибірки більший.
Загалом, якщо\(np \ge 5\) і\(nq \ge 5\), то нормальне наближення дає хорошу, але не ідеальну оцінку для біноміального розподілу. Коли використовувався зразок розміром 6,\(np = 3.6\) який менше 5. Крім того\(nq = 6(0.4) = 2.4\), що менше 5, теж. Тому використання нормального наближення для зразків, які малі, не є гарною стратегією.
Крок 7 - Знайдіть приблизне p-значення за допомогою Розподіл вибірки пропорцій
До цього моменту дискусія йшла про кількість людей. Коли проводиться вибірка, яка виробляє категоріальні дані, ці числа або підрахунки також можуть бути представлені у вигляді пропорцій, розділивши кількість успіхів на розмір вибірки. Таким чином, замість того, щоб дослідник сказав, що 4 з 6 людей вважають, що власник несе відповідальність, дослідник міг би сказати, що 66,7% людей вважають, що власник несе відповідальність. Це призводить до концепції розгляду пропорцій, а не підрахунків, що означає, що замість розподілу складається з кількості успіхів, представлених x, він складається з вибіркової частки успіхів, представлених \(\hat{p}\).
Відступ 7 - Розподіл вибірки пропорцій
Оскільки біноміальний розподіл містить всі можливі підрахунки кількості успіхів і воно приблизно нормально розподіляється, і оскільки всі рахунки можуть бути перетворені в пропорції шляхом ділення на розмір вибірки, то розподіл також приблизно нормально розподіляється.\(\hat{p}\) Цей розподіл має середнє і стандартне відхилення, яке можна знайти, розділивши середнє і стандартне відхилення біноміального розподілу на розмір вибірки n.
Середнє значення всіх пропорцій вибірки - це середнє число успіхів, поділене на n.
\(\mu_{\hat{p}} = \dfrac{\mu}{n} = \dfrac{np}{n} = p\)Це говорить про те, що середнє значення всіх можливих пропорцій вибірки дорівнює істинній пропорції для населення.
\[\mu_{\hat{p}} = p\]
Стандартне відхилення всіх пропорцій вибірки - це стандартне відхилення числа успіхів, поділене на n.
\(\sigma_{\hat{p}} = \dfrac{\sigma}{n} = \sqrt{\dfrac{npq}{n^2}} = \sqrt{\dfrac{pq}{n}}\ or\ \sqrt{\dfrac{p(1- p)}{n}}\)
\[\sigma_{\hat{p}} = \sqrt{\dfrac{pq}{n}}\ \ \ \ or \ \ \ \ \sigma_{\hat{p}} = \sqrt{\dfrac{p(1- p)}{n}}\]
Основну формулу z тепер\(z = \dfrac{x − \mu}{\sigma}\) можна переписати, знаючи, що в розподілі пропорцій вибірки результати зразка, які раніше були представлені, тепер\(X\) можуть бути представлені\(\hat{p}\). Середнє, тепер\(\mu\) можна представити з\(p\), так як\(\mu_{\hat{p}} = p\) і стандартне відхилення тепер\(\sigma\) можна представити з\(\sqrt{\dfrac{p(1- p)}{n}}\) так\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1- p)}{n}}\). Тому для розподілу вибірки пропорцій зразка формулою z\(z = \dfrac{x − \mu}{\sigma}\) стає
\[z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}.\]
Застосовують це поняття ймовірності до гіпотези про відповідальність за самостійне водіння автомобіля в ДТП.
Пам'ятайте, що гіпотези для людей, які вважають, що власник несе відповідальність, є:\(H_0: p = 0.60\),\(H_1: p > 0.60\). У первісній проблемі дослідник виявив, що 4 з 6 людей вважають, що власник несе відповідальність. Яку гіпотезу підтверджують ці дані, якщо рівень значущості дорівнює 0,10?
З тих\(\mu_{\hat{p}} = p\) пір середнє значення становить 0,60 (від нульової гіпотези). 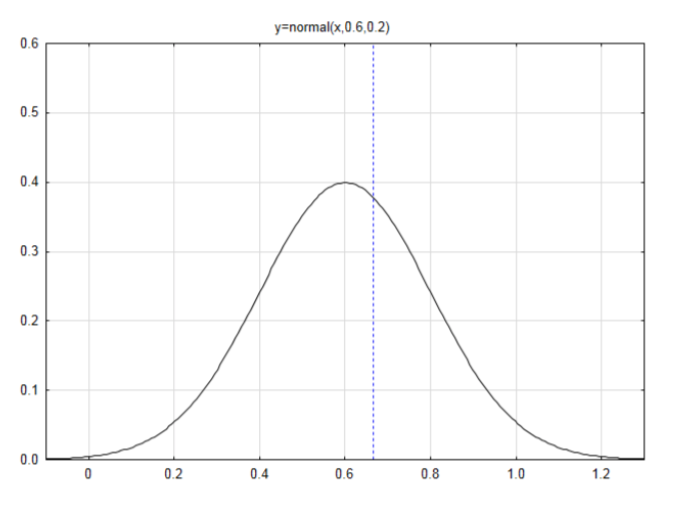
З тих\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1-p)}{n}} = \sqrt{\dfrac{0.6(0.4)}{6}} = 0.2\) пір стандартне відхилення становить 0,2.
Намалюйте мітку нормальної кривої із середнім значенням 0,6 та a
стандартне відхилення 0,2.
Якщо даних 4, то пропорція вибірки,
\(\hat{p} = \dfrac{x}{n} = \dfrac{4}{6} = 0.6667\)
Знайдіть оцінку z, якщо дані 4.
\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}\)\(z = \dfrac{0.6667 - 0.6}{0.2} = 0.33\)
Область зліва - це\(A_L = 0.6304\). Оскільки напрямок крайнього - вправо, відніміть площу вліво від 1, щоб отримати\(A_R = 0.3696\).
Порівняйте цей результат з результатом, знайденим при використанні нормального наближення до біноміального розподілу. Зверніть увагу, що обидва результати абсолютно однакові. Це має відбуватися щоразу, за умови, що немає округлення чисел. Причина, що це сталося, полягає в тому, що кількість успіхів може бути представлена як кількість або пропорції. Розподіли однакові, хоча вісь x позначається по-різному. Розділіть z бали для нормального наближення на розмір вибірки 6, і ви отримаєте z бали для розподілу вибірки.
Перевірте гіпотезу ще раз, якщо дослідник виявить, що 400 з 600 людей вважають, що власник несе відповідальність.
З тих\(\mu_{\hat{p}} = p\) пір середнє значення становить 0,60 (від нульової гіпотези).
З тих\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1-p)}{n}} = \sqrt{\dfrac{0.6(0.4)}{600}} = 0.02\) пір стандартне відхилення становить 0,02.
Якщо дані 400, то пропорція вибірки,\(\hat{p} = \dfrac{x}{n} = \dfrac{400}{600} = 0.66667\)
\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}\)\(z = \dfrac{0.66667 - 0.6}{0.02} = 3.33\)
Область зліва - це\(A_L = 0.9996\). Оскільки напрямок крайнього - вправо, відніміть площу вліво від 1, щоб отримати\(A_R = 0.0004\). Точніше, це 0.000430.
Висновок для перевірки гіпотез про категоричних даних.
До цього часу багато студентів задаються питанням, чому існують три методи і чому метод біноміального розподілу не єдиний, який використовується, оскільки він виробляє точне p-значення. Одним з обґрунтувань використання останнього методу є порівняння результатів обстежень або інших даних. Уявіть, якби одна інформаційна організація повідомила про свої результати опитування, оскільки 670 з 1020 були на користь, тоді як інша організація повідомила, що виявила, що 630 з 980 були на користь. Порівняння між ними було б важко без перетворення їх у пропорції, тому третій метод, який використовує пропорції, є методом вибору. Коли розмір вибірки досить великий, між методами немає великої різниці. Для менших зразків доцільніше використовувати біноміальний розподіл.
Роблячи висновки з використанням кількісних даних
Стратегія здійснення висновків з кількісними даними використовує розподіли вибірки так само, як вони використовувалися для здійснення висновків про пропорції. У цьому випадку нормальний розподіл використовувався для моделювання розподілу пропорцій зразка, р. За допомогою кількісних даних ми знаходимо середнє значення, тому нормальний розподіл буде використовуватися для моделювання розподілу вибіркових середніх, х.
Щоб продемонструвати це, буде використано невелике населення. Це населення складається з 50 штатів США плюс округ Колумбія та 5 територій США Американське Самоа, Гуам, Північні Маріанські острови, Пуерто-Рико та Віргінські острови, кожен з яких має по одному представнику в Конгресі з обмеженими повноваженнями голосу. Надано гістограму, що показує розподіл кількості представників в державі або території. На графіку наведено нормальний розподіл, заснований на тому, що середнє значення цієї популяції становить 7,875 представників і стандартне відхилення 9,487. Розподіл позитивно перекошений і не може бути змодельований нормальною кривою, яка знаходиться на графіку.
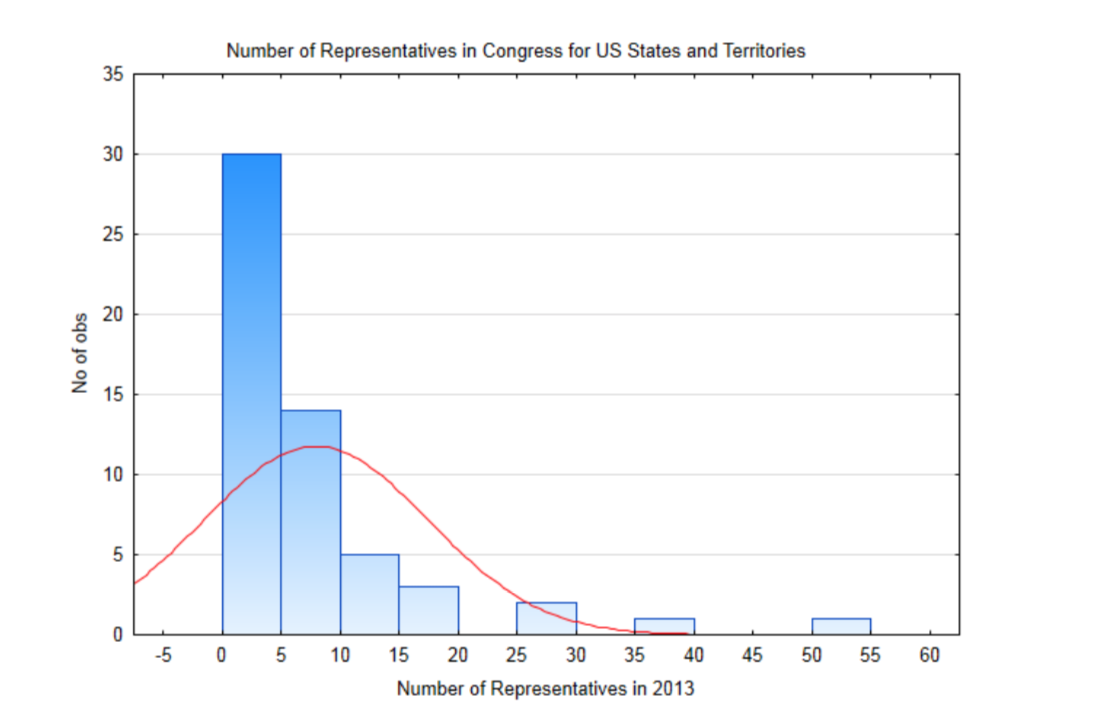
Майте на увазі, що насправді середнє і стандартне відхилення, які є параметрами, не відомі, і тому ми зазвичай пишемо гіпотези про них. Однак для цієї демонстрації необхідна невелика популяція з відомим середнім і стандартним відхиленням. Цим можна проілюструвати, що відбувається, коли повторні зразки однакового розміру витягуються з цієї сукупності, з заміною, а засоби кожного зразка знаходять і стають частиною розподілу вибіркових засобів.
Розподіл вибірки середніх зразків (розподіл x) містить всі можливі вибіркові засоби, які теоретично можна було б отримати, якщо використовувався випадковий процес відбору, із заміною. Кількість можливих вибіркових засобів можна дізнатися, використовуючи основне правило підрахунку. Намалюйте лінію, щоб представити кожну державу/територію, яка буде вибрана. У рядку напишіть кількість варіантів, щоб воно виглядало так:
| Варіанти: | 56 | 56 | 56 | 56 | 56 |
| Держава: | 1 | 2 | 3 | 4... | п |
Якщо наш розмір вибірки дорівнює 40, то\(56^{40}\) можливі зразки, які можна було б вибрати, що дорівнює\(8.46 \times 10^{69}\). Тобто багато можливих зразків. Для цієї демонстрації буде взято всього 10 000 зразків розміром 40. Розподіл цих зразків означає, коли це було зроблено, показано на гістограмі нижче.
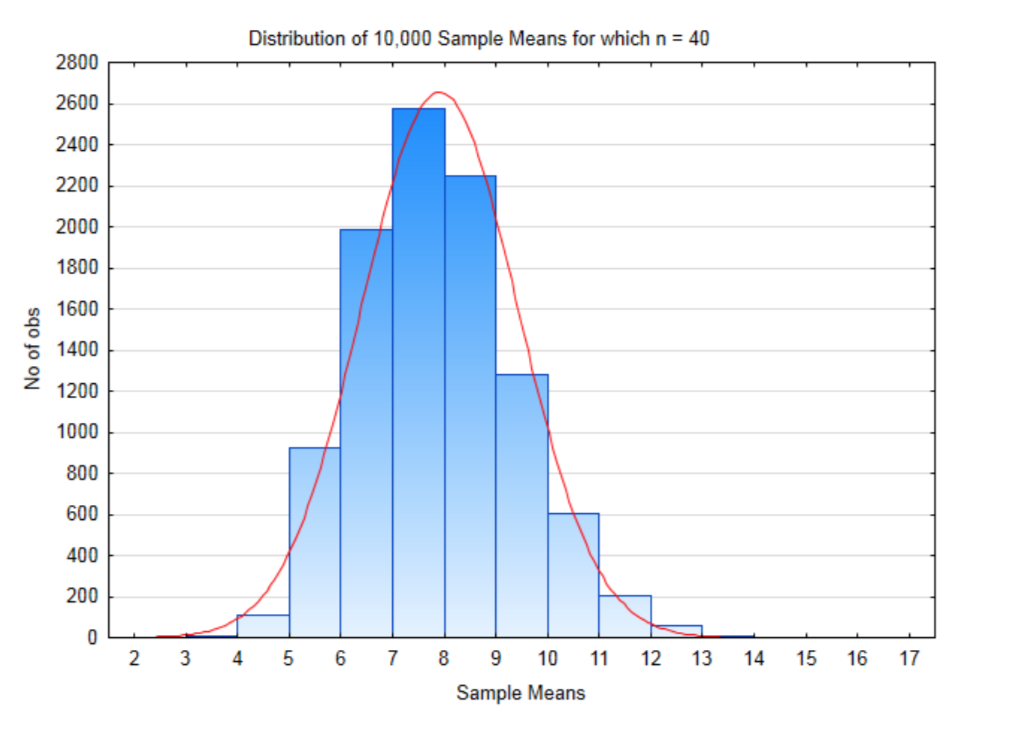
Середнє значення всіх цих засобів вибірки становить 7,8748, а стандартне відхилення - 1,502. Зверніть увагу, що середнє значення всіх цих вибіркових засобів майже точно таке ж, як і середнє значення початкової сукупності. Також зверніть увагу, що стандартне відхилення всіх цих вибіркових засобів набагато менше стандартного відхилення популяції. Це підсумовано в таблиці нижче.
| Населення | Розподіл вибірки | |
|---|---|---|
| Середнє | 7,875 | 7.8748 |
| Стандартне відхилення | 9.487 | 1.502 |
Наступний графік має як вихідні дані, так і вибіркові засоби на ньому. Зверніть увагу, як дві нормальні криві зосереджені приблизно в одному місці, але крива для зразка означає вужчу. Це показує, що коли зразки достатнього розміру взяті з будь-якої популяції, засоби цих зразків будуть близькі до засобів популяції.
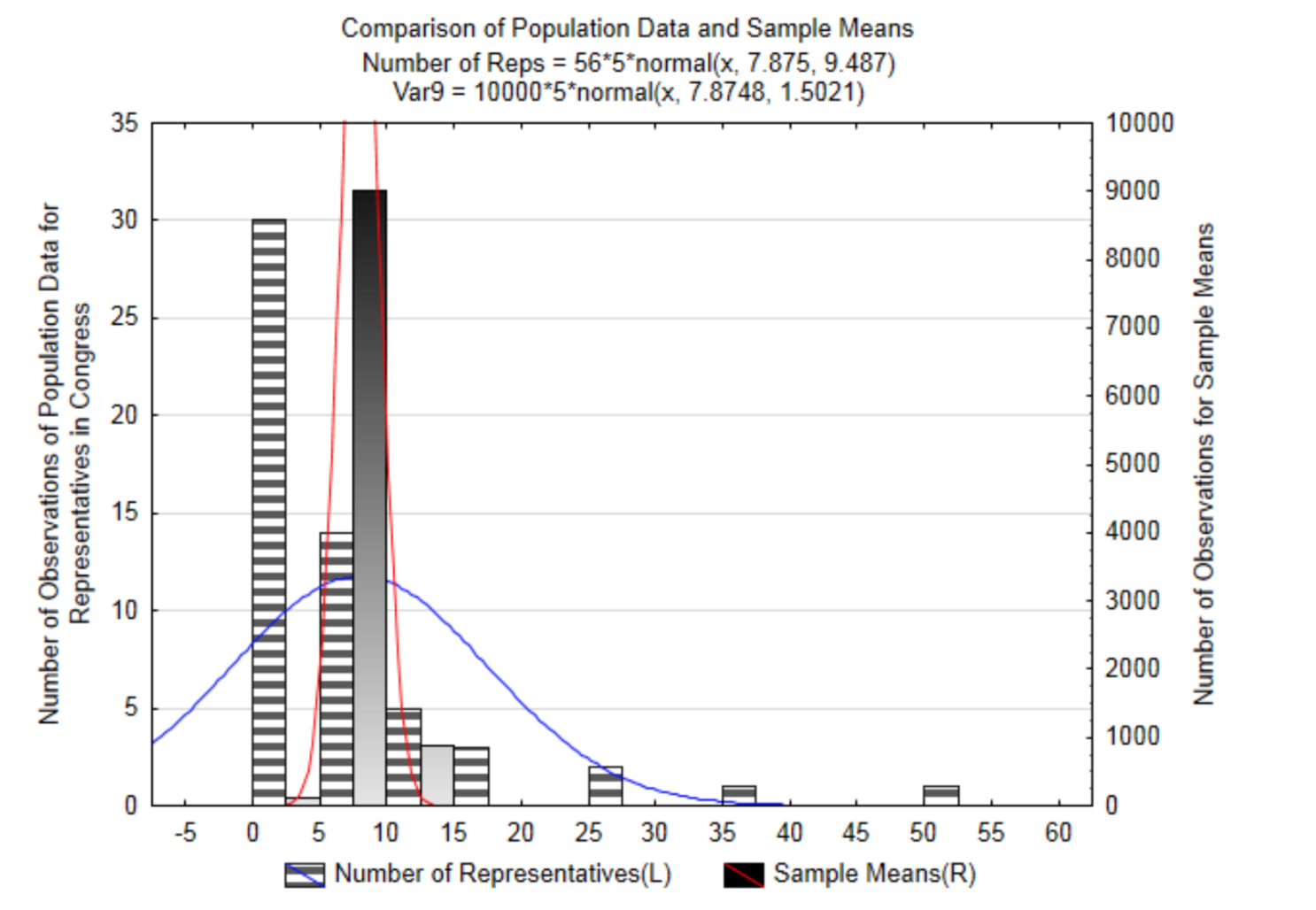
Тепер ми готові обговорити центральну граничну теорему. Ця теорема стверджує, що для будь-якого набору кількісних даних із середнім значенням μ і стандартним відхиленням σ середнє значення всіх можливих вибіркових засобів дорівнюватиме середньому чисельності населення. Стандартне відхилення всіх засобів вибірки, яке ще називають стандартною похибкою, буде дорівнювати стандартному відхиленню популяції, розділеної на квадратний корінь n.
\[\mu_{\bar{x}} = \mu\]
і
\[\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}.\]
Він також говорить, що розподіл вибіркових засобів буде нормальним, якщо розмір вибірки досить великий (як правило, вважається 30 або більше). Якщо початкова сукупність зазвичай розподілена, то розподіл вибіркових засобів буде зазвичай розподілений для будь-якого розміру вибірки.
Перш ніж робити приклад, важливо буде побачити ефект розмірів вибірки. Порівняйте наступні 4 графіки, які показують розподіл вибіркових засобів для зразків розміром 40, 30, 20 і 10.
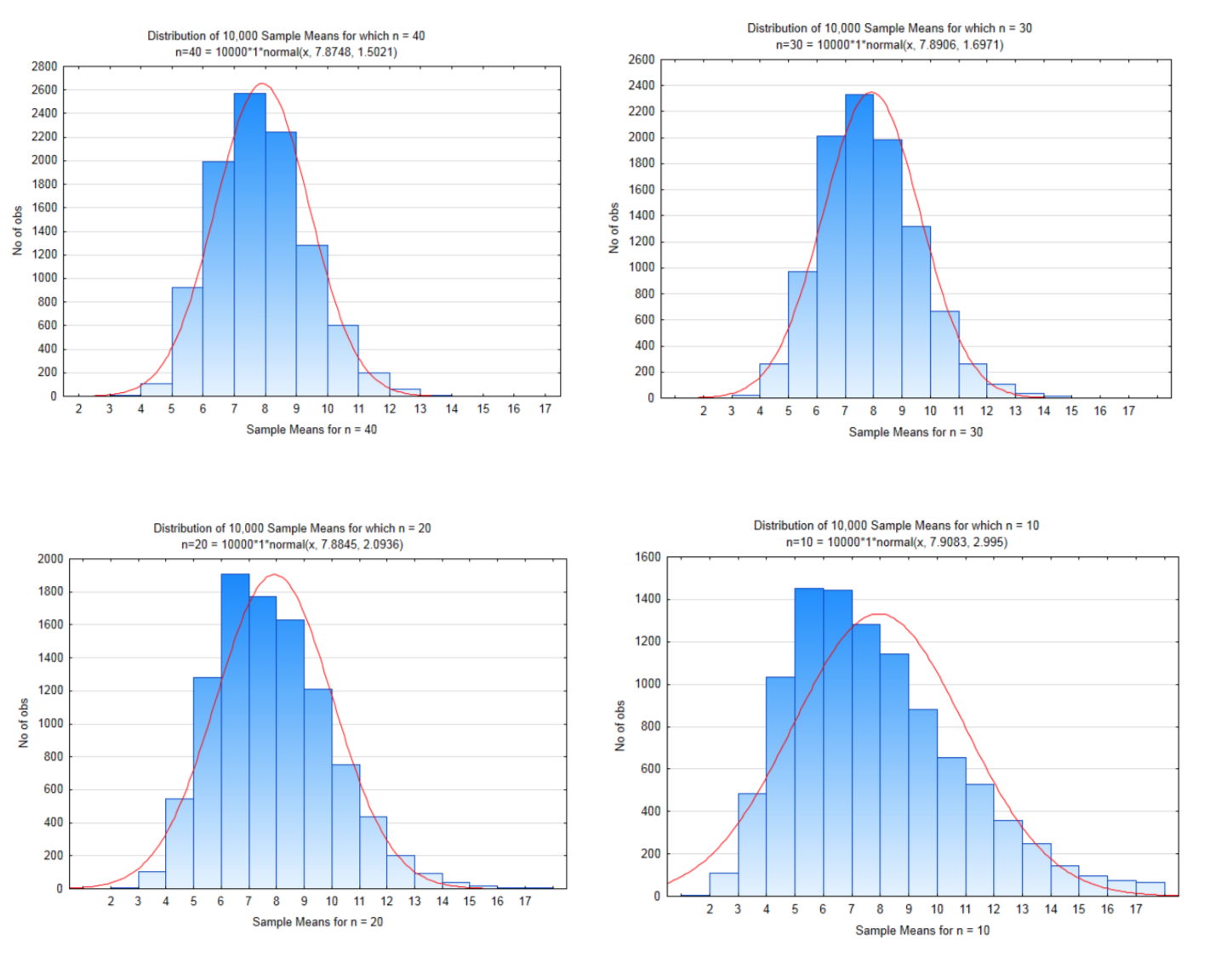
Зверніть увагу, як розподіли стають більш перекосованими, оскільки розмір вибірки зменшується. Зверніть увагу також, що середнє значення вибіркових засобів все ще приблизно дорівнює середньому чисельності населення, але стандартні відхилення стають більшими, оскільки розмір вибірки стає меншим. Це означає, що існує більше змін у вибіркових засобах з малими розмірами вибірки, ніж при великих розмірах вибірки.
| Населення | \(n = 40\) | \(n = 30\) | \(n = 20\) | \(n = 10\) | |
|---|---|---|---|---|---|
| Середнє | 7,875 | \ (n = 40\)» style="вертикальне вирівнювання: середина; ">7.8748 | \ (n = 30\)» style="вертикальне вирівнювання: середина; ">7.8906 | \ (n = 20\)» style="вертикальне вирівнювання: середина; ">7.8845 | \ (n = 10\)» style="вертикальне вирівнювання: середина; ">7.9083 |
| Стандартне відхилення | 9.487 | \ (n = 40\)» style="вертикальне вирівнювання: середина; "> 1.5021 | \ (n = 30\)» style="вертикальне вирівнювання: середина; "> 1.6971 | \ (n = 20\)» style="вертикальне вирівнювання: середина; "> 2.0936 | \ (n = 10\)» style="вертикальне вирівнювання: середина; "> 2.995 |
| Розрахункове стандартне відхилення за допомогою \(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\) |
\ (n = 40\)» style="вертикальне вирівнювання: середина; "> 1.500 | \ (n = 30\)» style="вертикальне вирівнювання: середина; ">1.732 | \ (n = 20\)» style="вертикальне вирівнювання: середина; "> 2.121 | \ (n = 10\)» style="вертикальне вирівнювання: середина; "> 3.000 |
Роблячи висновки про кількісні дані, основну\(z\) формулу тепер\(z = \dfrac{x − μ}{\sigma}\) можна переписати, знаючи, що при розподілі вибіркових засобів результати вибірки, які раніше були представлені, тепер\(x\) можуть бути представлені\(\bar{x}\). Середнє, як і раніше\(\mu\) буде представлено з\(\mu\), так як\(\mu_{\bar{x}} = \mu\) і стандартне відхилення тепер\(\sigma\) можна представити\(\dfrac{\sigma}{\sqrt{n}}\) з\(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\)
Тому для відбору проб розподілу засобів,\(z\) формулою,\(z = \dfrac{x − μ}{\sigma}\) стає
\[z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}.\]
Настав час використовувати центральну граничну теорему для перевірки гіпотези.
Приклад 7
Приклад 7 Меркурій в рибі не є здоровим і накладаються обмеження на кількість риби, яку слід вживати в їжу. Припустимо, дослідник хотів дізнатися, чи середня концентрація метилртуті на кілограм тканини риби перевищувала максимальну рекомендовану межу 300 мкг/кг. Якщо середня концентрація буде більше 300, рибальство буде закрито, інакше воно залишиться відкритим. Припустимо також, що стандартне відхилення для популяції є\(\sigma = 50 \mu g/kg\). Дослідник ловить 36 риб. Середня концентрація зразка становить 310.
Гіпотези, що підлягають перевірці, такі:
\(H_0: \mu = 300\)
\(H_1: \mu > 300\)
\(\alpha = 0.1\)
Так як вся інформація, яка потрібна, наводиться в задачі, насамперед потрібно знайти\(z\) бал.
\(z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}} = \dfrac{310 - 300}{\dfrac{50}{\sqrt{36}}} = 1.2.\)
Наступним кроком буде пошук вгору 1.20 в стандартних звичайних таблицях розподілу. Це дає область зліва від\(A_L=0.8849\) і тому область праворуч\(A_R = 0.1151\). Це p-значення.
Оскільки p-значення більше рівня значущості, робиться висновок, що середня концентрація метилртуті в тканині риб не значно перевищує 300\(\mu\) г/кг (\(z\)= 1,20,\(p\) = 0,1151,\(n\) = 36). Тому рибальство не буде закрито для риболовлі
Приклад 8
За однією з оцінок, середній час очікування субсидованого житла для бездомних становить 35 місяців. (www.stcloudstate.edu/reslife/... Statistics.pdf переглянуто 9/13/13) Припустимо, що розподіл разів є нормальним, а стандартне відхилення становить 10 місяців. Одне місто оцінює свою поточну програму та перевіряє, чи є вона ефективною та виправдовує подальше фінансування. Якщо середній час очікування менше 35 місяців, програма продовжиться. В іншому випадку програма буде замінена на іншу програму.
Гіпотези, що підлягають перевірці, такі:
- \(H_0: \mu = 35\)
- \(H-1: \mu < 35\)
\(\alpha = 0.01\)
Час очікування (в місяцях) двадцяти осіб, які нещодавно отримали субсидоване житло, зафіксовано нижче.
| 44 | 23 | 26 | 27 | 22 | 33 | 20 | 28 | 8 | 22 |
| 23 | 19 | 12 | 23 | 12 | 7 | 17 | 4 | 18 | 33 |
Оскільки нам дані, ми повинні знайти середнє значення зразка, перш ніж знайти оцінку z.
\(\bar{x} = 21.05\)
\(z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}} = \dfrac{21.05 - 35}{\dfrac{10}{\sqrt{20}}} = -6.24.\)
Оскільки напрямок крайнього ліворуч знаходимо область зліва на стандартній нормальній таблиці розподілу. Найнижча оцінка z, яку ми знаходимо на цій таблиці, становить -3.49. Площа зліва від -3.49 дорівнює 0.0002. Йдучи ще далі вліво, площа буде менше цього. Тому p-значення для цих даних становить <0.0002. Кількість часу очікування до отримання людьми субсидованого житла за діючою програмою значно менше 35 місяців (z = -6,24, р < 0,0002, n = 20). Виходячи з правила прийняття рішення, програма є ефективною і буде продовжувати фінансуватися.
